what is -f+2+4f=8-3f
Answers
Answer:
f=1
Step-by-step explanation:
You're welcome :)
3f + 2 = 8 - 3f
6f = 6
f = 1
Related Questions
Identify The Points In Figure 1 that Correnspond Q and S
Answers
Answer:
Step-by-step explanation:
s
The back and forward tangents AV, and VB of a highway meet at station 30+75.00. The angle of intersection, I, is 32°00'. It is desired to connect these two tangents by a circular curve whose degree of curve, by the chord definition, is Da=4°00'.
a) Calculate, R, the radius of this curve, T, the tangent distance, L, the length of the curve, M, the middle ordinate, E, the external distance, and the stations of the beginning of curve, A, and its end, B
Answers
Degree of curve, by the chord definition, is '.Angle of intersection of the back and forward tangents, I = 32°00'.
Station where the back and forward tangents meet,
P = 30+75.00Approach:Here, we will first calculate the degree of curvature (D) using the chord definition of degree of curvature. After that, we will find the radius of curvature (R) using the formula:
R = L²/24R is the radius of curvature, L is the length of the curve. T and M will be calculated using the formulas:
T = R tan(D/2)M
= R(1-cos(D/2))
E = Rsec(D/2) - R
Where E is the external distance of the curve.The station of the beginning of the curve is calculated by subtracting T from the station of the point where tangents meet while the station of the end of the curve is calculated by adding L to the station of the beginning of the curve.Solution:Degree of curve (by chord definition) = Da = 4°00'.
Therefore, the degree of curvature (D) = 4°00' using the chord definition of degree of curvature.Radius of curvature (R) = L²/24Therefore, the station of the beginning of the curve is 30+71.77 and the station of the end of the curve is 30+156.98.
To know more about tangents meet visit:
https://brainly.com/question/12089275
#SPJ11
The radius (R) of the curve is approximately 1432.5 feet. The tangent distance (T) is approximately 795.5 feet. The length of the curve (L) is approximately 502.3 feet. The middle ordinate (M) and external distance (E) are both approximately 37.2 feet. The station of the beginning of the curve (A) is 30+75.00 and the station of the end of the curve (B) is approximately 31+77.3.
To calculate the radius (R) of the circular curve connecting the tangents, we can use the formula:
R = 5730 / Da
Given Da = 4°00', substituting the values we get:
R = 5730 / 4 = 1432.5 feet
Next, to find the tangent distance (T), we can use the formula:
T = R * tan(I/2)
Given I = 32°00', substituting the values we get:
T = 1432.5 * tan(32°/2) ≈ 795.5 feet
To calculate the length of the curve (L), we can use the formula:
L = 2 * π * R * (I/360)
Given R = 1432.5 and I = 32°00', substituting the values we get:
L = 2 * π * 1432.5 * (32°/360) ≈ 502.3 feet
The middle ordinate (M) is given by:
M = R - sqrt(R^2 - (T/2)^2)
Substituting the values, we get:
M = 1432.5 - sqrt(1432.5^2 - (795.5/2)^2) ≈ 37.2 feet
The external distance (E) is given by:
E = R * (1 - cos(I/2))
Substituting the values, we get:
E = 1432.5 * (1 - cos(32°/2)) ≈ 37.2 feet
Finally, the station of the beginning of the curve (A) is 30+75.00 and the station of the end of the curve (B) can be calculated by adding the length of the curve (L) to the station of the beginning of the curve:
B = A + L = 30+75.00 + 502.3 ≈ 31+77.3
Learn more about curve
https://brainly.com/question/30511233
#SPJ11
(12x13)=12x(13x17) what property
A. Associate property
B. Commutative property
C.Distributive Property
Answers
Answer:
Distributive property
compute the critical value za/2 that corresponds to a 83% level of confidence
Answers
The critical value zₐ/₂ that corresponds to an 83% level of confidence is approximately 1.381.
To find the critical value zₐ/₂, we need to determine the value that leaves an area of (1 - α)/2 in the tails of the standard normal distribution. In this case, α is the complement of the confidence level, which is 1 - 0.83 = 0.17. Dividing this value by 2 gives us 0.17/2 = 0.085.
To find the z-value that corresponds to an area of 0.085 in the tails of the standard normal distribution, we can use a standard normal distribution table or a statistical calculator. The corresponding z-value is approximately 1.381.
Therefore, the critical value zₐ/₂ that corresponds to an 83% level of confidence is approximately 1.381.
For more questions like Critical value click the link below:
https://brainly.com/question/32607910
#SPJ11
A student studying a foreign language has 50 verbs to memorize. The rate at which the student can memorize these verbs is proportional to the number of verbs remaining to be memorized, 50 – y, where the student has memorized y verbs. Assume that initially no verbs have been memorized and suppose that 20 verbs are memorized in the first 30 minutes.
(a) How many verbs will the student memorize in two hours?
(b) After how many hours will the student have only one verb left to memorize?
Answers
The number of verbs memorized after two hours (t = 120) is:y = 50 - 15(30/2)^(-1/30)(120)= 45.92. Therefore, the student will memorize about 45 verbs in two hours.
(a) A student studying a foreign language has 50 verbs to memorize. Suppose the rate at which the student can memorize these verbs is proportional to the number of verbs remaining to be memorized, 50 – y, where the student has memorized y verbs. Initially, no verbs have been memorized.
Suppose 20 verbs are memorized in the first 30 minutes.
For part a) we have to find how many verbs will the student memorize in two hours.
It can be seen that y (the number of verbs memorized) and t (the time elapsed) satisfy the differential equation:
dy/dt
= k(50 – y)where k is a constant of proportionality.
Since the time taken to memorize all the verbs is limited to two hours, we set t = 120 in minutes.
At t
= 30, y = 20 (verbs).
Then, 120 – 30
= 90 (minutes) and 50 – 20
= 30 (verbs).
We use separation of variables to solve the equation and integrate both sides:(1/(50 - y))dy
= k dt
Integrating both sides, we get;ln|50 - y|
= kt + C
Using the initial condition, t = 30 and y = 20, we get:
C = ln(50 - 20) - 30k
Solving for k, we get:
k = (1/30)ln(30/2)Using k, we integrate to find y as a function of t:
ln|50 - y|
= (1/30)ln(30/2)t + ln(15)50 - y
= e^(ln(15))e^((1/30)ln(30/2))t50 - y
= 15(30/2)^(-1/30)t
Therefore,
y = 50 - 15(30/2)^(-1/30)t
Hence, the number of verbs memorized after two hours (t = 120) is:y = 50 - 15(30/2)^(-1/30)(120)
= 45.92
Therefore, the student will memorize about 45 verbs in two hours.
(b) Now, we are supposed to determine after how many hours will the student have only one verb left to memorize.
For this part, we want y
= 1, so we solve the differential equation:
dy/dt
= k(50 – y)with y(0)
= 0 and y(t)
= 1
when t = T.
This gives: k
= (1/50)ln(50/49), so that dy/dt
= (1/50)ln(50/49)(50 – y)
Separating variables and integrating both sides, we get:
ln|50 – y|
= (1/50)ln(50/49)t + C
Using the initial condition
y(0) = 0, we get:
C = ln 50ln|50 – y|
= (1/50)ln(50/49)t + ln 50
Taking the exponential of both sides, we get:50 – y
= 50(49/50)^(t/50)y
= 50[1 – (49/50)^(t/50)]
When y = 1, we get:
1 = 50[1 – (49/50)^(t/50)](49/50)^(t/50)
= 49/50^(T/50)
Taking natural logarithms of both sides, we get:
t/50 = ln(49/50^(T/50))ln(49/50)T/50 '
= ln[ln(49/50)/ln(49/50^(T/50))]T
≈ 272.42
Thus, the student will have only one verb left to memorize after about 272.42 minutes, or 4 hours and 32.42 minutes (approximately).
To know more about Number visit :
https://brainly.com/question/3589540
#SPJ11
It takes billy 6 minutes to walk 1.5 km. How long will it take billy to walk 9km?
Answers
Answer:
It will take Billy 36 minutes to walk 9km.

Answer:
\(\boxed{\tt 36 \ minutes}\)
Step-by-step explanation:
Let's make a proportion using the following setup:
\(\frac{minutes}{kilometers} =\frac{minutes}{kilometers} \\\)
We know it takes Billy 6 minutes to walk 1.5 kilometers.
\(\frac{6\ minutes}{1.5\ kilometers} =\frac{minutes}{kilometers}\)
We don't know how long it takes him to walk 9 kilometers, so we can say it takes him x minutes to walk 9 kilometers.
\(\frac{6\ minutes}{1.5\ kilometers} =\frac{x\ minutes}{9\ kilometers}\)
\(\frac{6}{1.5} =\frac{x}{9}\)
Now, solve for x. To do this, isolate x on one side of the proportion. x is being divided by 9. The inverse of division is multiplication. Multiply both sides of the proportion by 9.
\(9*\frac{6}{1.5} =\frac{x}{9}*9\)
\(9*\frac{6}{1.5} =x\)
\(9*4=x\)
\(36=x\)
x= 36 minutes
It will take Billy 36 minutes to walk 9 kilometers.
What is the surface area of this cylinder?

Answers
Answer:
1067.6 m²Step-by-step explanation:
Given that
r = 10 mh = 7 mπ ≈ 3.14Find the surface area of the cylinder!
Equation =
2πr × (r+h) =(2 × 3.14 × 10) × (10 + 7) =
62.8 × 17 ≈
1067.6 m²The surface area of the cylinder ≈ 1067.6 square metres
_________________
#Indonesian - kexcvi
Answer:
Use this formula to calculate for the surface area of cylinder.
Step-by-step explanation:
A=2π r h+2 π r^2.
use r = 10 m and h = 7 m
2 (3.14) (10) 7 + 2 (3.14) 10 ^2. = 439.6 + 628 = 1067.6
round to the nearest hundredths = 1068
Rosa earned a total of $34 by selling 17 cups of lemonade. How many cups of lemonade does Rosa need to sell in all to earn $46? Assume the relationship is directly proportional.
Answers
Answer:
23
Step-by-step explanation:
Because 2 dollar each cup. so 2 times 23 is $46. 5 star if this help thanks:)
Sarah has been training for a marathon, which will cover a distance of 42.195 km. In training
she has consistently run 1km each 6 minutes. How long will it take Sarah to complete the
Marathon if she runs at this pace consistently throughout the race?
Answers
Answer:
4 hours 21 minutes 17 seconds.
Step-by-step explanation:
1km = 6 minutes
42.195km = ?
42.195 × 6 = 253 minutes 17 seconds = 4 hours 21 minutes 17 seconds.
Answer:
4 hours 21 minutes 17 seconds.
Step-by-step explanation:
A Buffalo school district randomly tests its employees to determine how many have gotten the flu shot this season. Their sample shows that 15 of them have gotten it, and 27 have not. Estimate the true proportion of employees in the district who have gotten a flu shot, with a 90% confidence level. Check conditions to see if you can use normal sampling distribution for sample proportion
Answers
Using the z-distribution, as we are working with a proportion, the 90% confidence level estimate for the true proportion of employees in the district who have gotten a flu shot is (0.2355, 0.4784).
What is a confidence interval of proportions?As long as there are 10 successes and 10 failures in the sample, that is, \(n\pi \geq 10\) and \(n(1 - \pi) \geq 10\), a confidence interval of proportions is given by:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which:
\(\pi\) is the sample proportion.z is the critical value.n is the sample size.In this problem, the parameters are:
\(n = 42, \pi = \frac{15}{42} = 0.3571, z = 1.645\)
We have the \(n\pi = 15, n(1 - \pi) = 27\), hence you can find the interval.
The lower limit of this interval is:
\(\pi - z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.3571 - 1.645\sqrt{\frac{0.3571(0.6429)}{42}} = 0.2355\)
The upper limit of this interval is:
\(\pi + z\sqrt{\frac{\pi(1-\pi)}{n}} = 0.3571 + 1.645\sqrt{\frac{0.3571(0.6429)}{42}} = 0.4787\)
The 90% confidence level estimate for the true proportion of employees in the district who have gotten a flu shot is (0.2355, 0.4784).
More can be learned about the z-distribution at https://brainly.com/question/25890103
Sketch the triangle ABC and solve it using the law of cosines. Round off your answers to the nearest integer. b = 60, c = 30, ∠A = 70∘
Ams: a = 57, ∠B = 81∘, and ∠C = 29∘
Answers
Answer:
Sure. Here are the steps on how to solve for the sides and angles of triangle ABC using the law of cosines:
Draw a sketch of triangle ABC.
Label the sides and angles of triangle ABC.
Label the known and unknown values.
Use the law of cosines to solve for the unknown side or angle.
In this case, we know the following:
Side b = 60
Side c = 30
Angle A = 70°
We need to solve for side a and angles B and C.
The law of cosines states that
a^2 = b^2 + c^2 - 2bc cos A
where a, b, and c are the sides of the triangle and A is the angle opposite side a.
Plugging in the known values, we get
a^2 = 60^2 + 30^2 - 2(60)(30) cos 70°
a^2 = 900 + 900 - 3600 cos 70°
a^2 = 1800 - 3600 cos 70°
a = sqrt(1800 - 3600 cos 70°)
a = 57
Therefore, side a is 57.
To solve for angle B, we can use the law of sines. The law of sines states that
\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}
Plugging in the known values, we get
\frac{57}{\sin 70°} = \frac{60}{\sin B}
\sin B = \frac{57 \sin 70°}{60}
\sin B = 0.774
B = \sin^{-1}(0.774)
B = 81°
Therefore, angle B is 81°.
To solve for angle C, we can use the fact that the sum of the angles of a triangle is 180°.
A + B + C = 180°
70° + 81° + C = 180°
C = 29°
Therefore, angle C is 29°.
Therefore, the sides and angles of triangle ABC are a = 57, b = 60, c = 30, A = 70°, B = 81°, and C = 29°.
Step-by-step explanation:
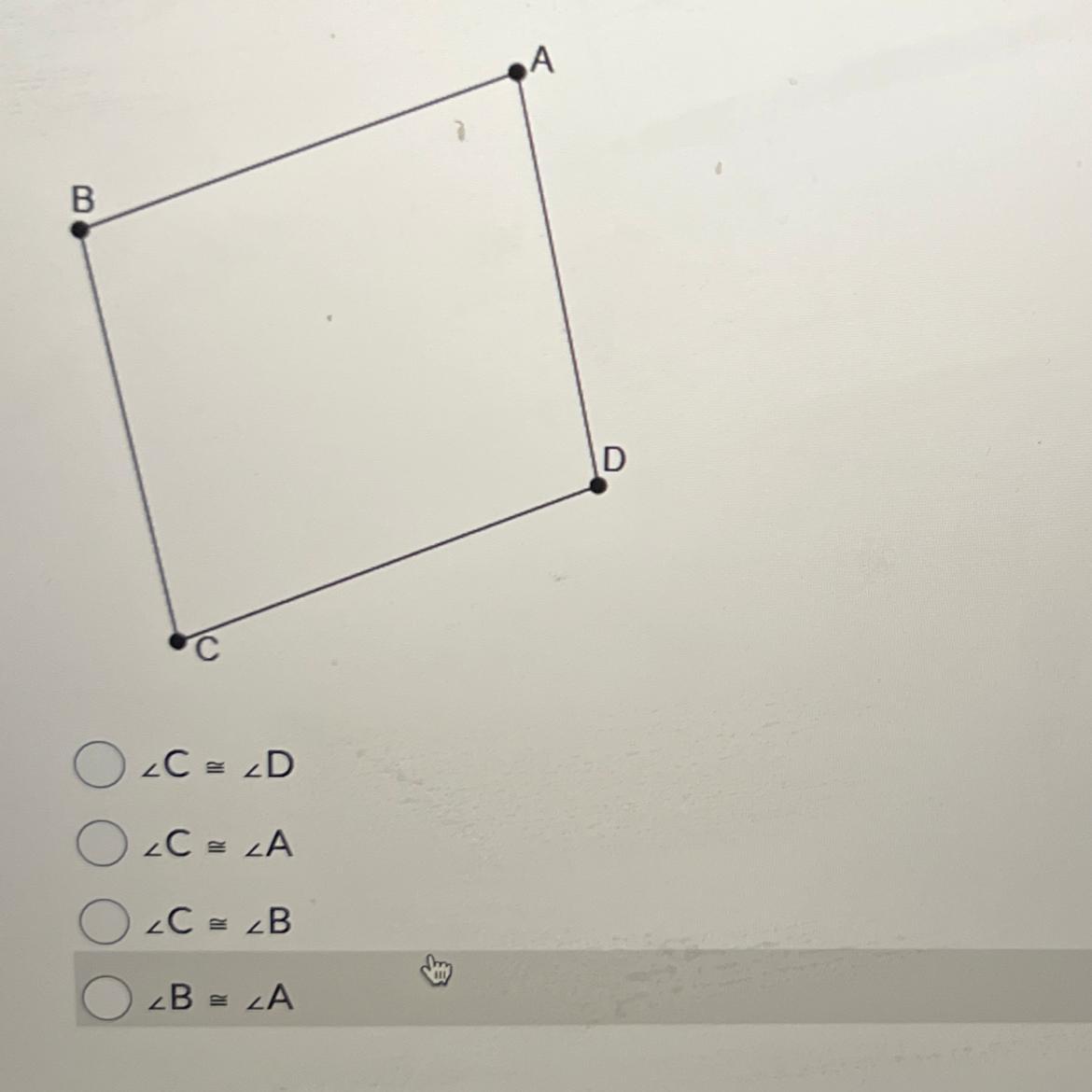
Which of the following statements must be true about parallelogram ABCD?
Answers
Answer:
\(\angle C \cong \angle A\)
Step-by-step explanation:
Opposite angles of a parallelogram are congruent.
In a class of 19 students, 12 are female and 13 have an A in the class. There are 4 students who are male and do not have an A in the class. What is the probability that a student chosen randomly from the class does not have an A?
answer is
6/19
Answers
× whats the point of this
The likelihood of selecting a classmate at random who does not have an A is 6/19.
What is probability?Probability is a number that expresses the likelihood or chance that a specific event will take place. Both proportions ranging from 0 to 1 and percentages ranging from 0% to 100% can be used to describe probabilities.
To find the probability of a student not having an A, we need to first find the total number of students who do not have an A.
The number of students who have an A is 13, so the number of students who do not have an A is:
19 - 13 = 6
Out of these 6 students, 4 are male and 2 are female.
So, the probability of choosing a student randomly who does not have an A is:
P(not A) = number of students without an A / total number of students
P(not A) = 6 / 19
Therefore, the probability of choosing a student randomly from the class who does not have an A is 6/19.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ2
Select the correct values of the five-number summary for the data set:
15, 17, 23, 21, 19, 20, 14, 25, 15, 24
Minimum: 14
Minimum: 15
Minimum: 13
1st quartile: 23
1st quartile: 14
1st quartile: 15
Median: 20
Median: 19
Median: 19.5
3rd quartile: 23
3rd quartile: 15
3rd quartile: 25
Maximum: 23
Maximum: 25
Maximum: 24
Answers
Answer:
Step-by-step explanation:
MULTIPLY BY 442 THEN DIVED 55 FROM YOUR CURRENT AWNSER
my cousin when in Vietnam was a personal banker for his Army buddies ... if they needed money mid-month he would give them $20 if you agreed to pay him $40 at month end on payday ... although he did not disclose his borrowing rate, what was the cost of money (APR) for his buddies who needed immediate gratification
Answers
The personal banker given lending arrangement, the APR for your cousin's buddies who borrowed $20 and repaid $40 at the end of the month would be 120%
The annual percentage rate (APR) for your cousin's lending arrangement, to make a few assumptions. That each lending transaction occurs on the first day of the month and is repaid on the last day of the same month. Based on these assumptions, calculate the effective APR as follows:
Calculate the interest charged for a $20 loan over one month:
Interest = $40 (repaid amount) - $20 (loaned amount) = $20
Divide the interest by the loan amount and multiply by 100 to get the monthly interest rate:
Monthly Interest Rate = (Interest / Loan Amount) ×100 = ($20 / $20) ×100 = 100%
Multiply the monthly interest rate by 12 to obtain the annual interest rate:
APR = Monthly Interest Rate ×12 = 100% ×12 = 120%
To know more about banker here
https://brainly.com/question/14328094
#SPJ4
What percent of data population falls between a z-score of -1. 5 and 0. 5
Answers
Around 62.47% of the data population is situated between a z-score of -1.5 and 0.5.
Assuming a standard normal distribution, the percentage of the data population that falls between a z-score of -1.5 and 0.5 can be calculated using a standard normal table or a calculator.
Using a standard normal table, we can find the area under the curve between z = -1.5 and z = 0.5.
The area to the left of z = 0.5 is 0.6915, and the area to the left of z = -1.5 is 0.0668. Therefore, the area between z = -1.5 and z = 0.5 is:
0.6915 - 0.0668 = 0.6247
So, approximately 62.47% of the data population falls between a z-score of -1.5 and 0.5.
Learn more about interpretation of z-scores here: brainly.com/question/14930959
#SPJ4
Which of the following statements are true? Select all that apply
*Picture Shown Above*

Answers
Suppose that either a member of the CS faculty or a student who is a CS major is chosen as a representative to a university committee. How many different choices are there for this representative if there are 9 members of the CS faculty and 114 CS majors and no one is both a faculty member and a student
Answers
The total number of different choices for the representative is 114
How to find different choices for the representative to the university committee?The number of choices for the representative to the university committee is the sum of the number of CS faculty members and the number of CS majors who are not faculty members.
Since no one can be both a faculty member and a student.
The number of choices for a faculty member is simply the number of members of the CS faculty, which is 9.
The number of choices for a CS major who is not a faculty member can be calculated by subtracting the number of CS faculty members from the total number of CS majors: 114 - 9 = 105.
Therefore, the total number of different choices for the representative is:
9 + 105 = 114
So there are 114 different choices for the representative to the university committee.
Learn more about combinatorics
brainly.com/question/31476844
#SPJ11
You are given a 1.41-g mixture of sodium nitrate and sodium chloride. You dissolve this mixture into 135 mL of water then add an excess of 0.542 M silver nitrate solution. You produce a white solid, which you then collect, dry, and measure. The white solid has a mass of 1.464 g.
a. If you had an extremely magnified view of the solution (to the atomic-molecular level), list the species you would see (include charges, if any).
b. Write the balanced net ionic equation for the reaction that produces the solid. Include phases and charges.
c. Calculate the percent sodium chloride in the original unknown mixture.
Answers
a. If we had an extremely magnified view of the solution, to the atomic-molecular level, the following species would be observed (including charges, if any) :2 Na+, NO3-, Ag+, and Cl-.b. The balanced net ionic equation for the reaction that produces the solid is: Ag+ + Cl- → AgCl↓c. Calculate the percent sodium chloride in the original unknown mixture:
1. Calculate the amount of AgCl precipitated. According to the balanced chemical reaction, 1 mol of AgNO3 reacts with 1 mol of NaCl to produce 1 mol of AgCl. A 0.542 M AgNO3 solution contains 0.542 mol/L of AgNO3.0.542 mol/L × 0.135 L = 0.07317 mol AgNO3 reacted with NaCl.0.07317 mol AgNO3 × (1 mol NaCl / 1 mol AgNO3)
= 0.07317 mol NaCl precipitated.2. Calculate the number of moles of NaCl and NaNO3 in the original sample.Mass of sample = 1.41 gMass of AgCl produced = 1.464 g Subtracting the mass of AgCl from the mass of the sample gives us the mass of NaCl and NaNO3 in the original sample:
Mass of NaCl and NaNO3 = 1.464 g − 1.41 g = 0.054 g.The percent of NaCl in the sample is given by: Mass of NaCl in the sample / Mass of the sample × 100 %= 0.067 g / 1.41 g × 100 %= 4.7%.Therefore, the percent of NaCl in the original mixture is 4.7%.
To know more about magnified visit:
https://brainly.com/question/32284838
#SPJ11
3) Generate and plot normal pdfs with o= 2 anddifferent u values at -1, 0 and -1 on the same graph. Provide the graph with a legend label.
Answers
Normal probability density function (pdf) with different mean values (u) at -1, 0 and 1 for a fixed variance (o= 2) can be plotted using the R software.
To generate and plot these pdfs, we can use the 'dnorm' function in R. The dnorn function takes three arguments;
x (vector of values), mean (mean value), and sd (standard deviation).
The code to plot the normal pdfs with the given mean values and standard deviation using R software is shown below:
# generate values for x <- seq(-10, 10, length=100)# calculate normal pdfs for mean values -1, 0, and 1 y1 <- dnorm(x, mean=-1,
sd =2) y2 <- dnorm (x, mean=0,
sd =2) y3 <- dnorm (x, mean=1, sd=2)
# Plot normal pdfs on the same graph plot(x, y1, type="l", col="blue", xlab="x", ylab="pdf")
lines(x, y2, type="l", col="red")
lines(x, y3, type="l", col="green")
legend(-10,0.4,)
legend=c("mean=-1", "mean=0", "mean=1"),
col=c("blue", "red", "green"),
lty=1)
To learn more on standard deviation:
https://brainly.com/question/24298037
#SPJ11

Dominic spent $8 on a book. He made $6 doing chores for a neighbor. What numbers represent the situations?
–8 and –6
–8 and 6
8 and –6
8 and 6
Answers
Answer:
-8 and 6
Step-by-step explanation:
he spent 8 on the book, therefore he had deduced 8 dollars, and earned 6, therefore he had increased 6 dollars
Answer:
I am guessing it is -8 and 6
Step-by-step explanation:
If Dominic spent $8 on a book, but only made $6, I believe it wil be -8, because he spent 8, and 6 because it's what he earned.
Hope this helps! :)
a restaurant wants to know if its customers like its new menu. in surveys 100 randomly selected customers over one week. what is the population in this study?
Answers
In terms of using specific terms in your answer, you should incorporate any keywords or phrases from the student's question that are relevant to your response.
For example, in response to the question "a restaurant wants to know if its customers like its new menu. in surveys 100 randomly selected customers over one week. what is the population in this study?" you might write:"
In this study, the population refers to the entire group of customers who might potentially like or dislike the restaurant's new menu.
While the study only surveyed 100 randomly selected customers over one week, the population could include all customers who visited the restaurant during that time period or even a larger group of potential customers who have not yet visited the restaurant."
for such more questions on randomly
https://brainly.com/question/25428940
#SPJ11
need answer quick
log √3 base 10 - 1/2 log 2 base 10
Answers
The value of ㏒₁₀√3 - 1 / 2 ㏒₁₀2 is 1 / 2.㏒₁₀(1.5)
Given: To evaluate ㏒₁₀√3 - 1 / 2 . ㏒₁₀2
What are logarithms?
If a equation is given in the form of aᵇ = c, then ㏒ₐc = b or in a definitive way a logarithm is the power to which a number must be raised in order to get a number. As here 'a' is raised to the power 'b' to given a number c, so the number base 'a' if be raised to some power of 'b' then it will yield a number 'c'.
For example, 10² = 100 which can be written as ㏒₁₀100 = 2 by the following property of logarithm that is ㏒ₐ(bⁿ) = n.㏒ₐb.
So, ㏒₁₀100 = ㏒₁₀10² = 2.㏒₁₀10 = 2 [ Another property ㏒ₐa = 1]
Some basic properties on logarithm operations are
1) ㏒ₙa + ㏒ₙb = ㏒ₙ(ab)
2) ㏒ₙa - ㏒ₙb = ㏒ₙ(a / b) [NOTE: ㏒ₙa - ㏒ₙb is not commutative]
3) ㏒ₐ(bⁿ) = n.㏒ₐb
4) ㏒ₐa = 1
Now let's solve the sum: ㏒₁₀√3 - 1 / 2 ㏒₁₀2
㏒₁₀√3 - 1 / 2 ㏒₁₀2 = ㏒₁₀(3)\(^{\frac{1}{2}}\) - 1 /2 .㏒₁₀2 [ Root means 1 / 2 power]
= 1 / 2.㏒₁₀(3) - 1 / 2.㏒₁₀(2) [ ㏒ₐ(bⁿ) = n.㏒ₐb ]
= 1 / 2.(㏒₁₀(3) - ㏒₁₀(2))
= 1 / 2.(㏒₁₀(3 / 2) [ ㏒ₙa - ㏒ₙb = ㏒ₙ(a / b) ]
= 1 / 2.㏒₁₀(1.5)
Hence value of ㏒₁₀√3 - 1 / 2 ㏒₁₀2 = 1 / 2.㏒₁₀(1.5)
Know more about "logarithm functions" here: https://brainly.com/question/20785664
#SPJ9
If f and g are differentiable functions for all real values of x such that f(2) = 5, g(2) = 3, f '(2) = 1, g '(2) = -2, then find h '(2) if h(x) = f(x) g(x).
Answers
Answer:
\(h'(2)=-7\)
Step-by-step explanation:
So we have:
\(h(x)=f(x)g(x)\)
Differentiate. Use the product rule:
\(h'(x)=f'(x)g(x)+f(x)g'(x)\)
Substitute 2 for x:
\(h'(2)=f'(2)g(2)+f(2)g'(2)\)
We know that f'(2) is 1, f(2) is 5, g(2) is 3, and g'(2) is -2. Make the appropriate substitutions:
\(h'(2)=(1)(3)+(5)(-2)\)
Simplify:
\(h'(2)=3-10\)
Subtract:
\(h'(2)=-7\)
Suppose that the volume of a right circular cylinder is 288 cubic meters and the area of its base is 16 square meters. What is the height of the cylinder?
A. 12 m
B. 16 m
C. 18 m
D. 14 m
Answers
Answer: 18
Step-by-step explanation:
288 / 16 = 18
Answer:
C) 18 m
Step-by-step explanation:
A study was run to determine if more than 30% of Cal State East Bay students work full-time. A random sample of 100 Cal State East Bay students had 36 work full-time. The p-value was found to be 0.0952. Group of answer choices There is a 9.52% chance that a random sample of 100 Cal State East Bay students would have more than our sample's 36 working full-time. There is a 9.52% chance that a random sample of 100 Cal State East Bay students would have more than our sample's 36 working full-time if exactly 30% of Cal State East Bay students work full-time. There is a 9.52% chance that a random sample of 100 Cal State East Bay students would have the same as our sample's 36 working full-time if exactly 30% of Cal State East Bay students work full-time. There is a 9.52% chance that a random sample of 100 Cal State East Bay students would have more than 30% working full-time.
Answers
The correct option id D. There is a 9.52% chance that a random sample of 100 Cal State East Bay students would have more than our sample's 36 working full-time
A study was conducted to determine if more than 30% of Cal State East Bay students work full-time.
The sample of Cal State East Bay students selected was random.
Out of 100 students, 36 were found to be working full-time.
The p-value was calculated to be 0.0952.
The probability of having more than 36 Cal State East Bay students working full-time out of a random sample of 100 students is 9.52% if exactly 30% of Cal State East Bay students work full-time.
Therefore, it is concluded that the null hypothesis cannot be rejected.
The p-value is greater than 0.05 which shows the significance level.
Hence, we accept the null hypothesis.
The null hypothesis states that the proportion of Cal State East Bay students who work full-time is not greater than 30%.
The alternate hypothesis states that the proportion of Cal State East Bay students who work full-time is greater than 30%.
The test is a right-tailed test.
The sample proportion is p = 0.36. The test statistic is given as Z = (p - P0) / √ [P0 (1 - P0) / n]Z = (0.36 - 0.30) / √ [(0.30) (0.70) / 100] = 1.76The p-value is given as 0.0392.
Since the p-value is less than 0.05, we can reject the null hypothesis.
Thus, we can conclude that more than 30% of Cal State East Bay students work full-time.
Hence, option D is the correct answer.
There is a 9.52% chance that a random sample of 100 Cal State East Bay students would have more than 30% working full-time.
To learn more about random sample
https://brainly.com/question/24466382
#SPJ11
Which statement about x in quadrilateral ABCD is true?

Answers
Answer:
Where are the options????
2/3x = 6
A. x = 9
B. x = 4
C. x = 18
D. x = 12
Answers
Answer:
x = 9
Step-by-step explanation:
2/3x = 6
Multiply each side by 3/2
3/2 * 2/3x = 6 * 3/2
x = 18/2
x = 9
Hope this helps
A store sells about 30 pants each week for Nu 800 each. The owner expects to lose one sale each week for every increase in price of Nu 40. a) Write an expression to represent the i) new price of a pant after n Nu 40 price increases. ii) expected number of pants that will be sold weekly after n price increases. b) Write a function to represent the expected weekly sales as a function of the number of price increases of Nu 40. c) Use the function to determine the price that will maximize totally sales.
Answers
The new price after the price increase of Nu 40 will be Nu 840.
How to calculate the price?The price of a pant after n Nu 40 price increases will be:
= 800 + 40
= 840
The expected weekly sales as a function of the number of price increases will be:
= n - 1) × 800
= (30 - 1) × 800
= 29 × 800
= 23200
Learn more about price on:
brainly.com/question/1153322
#SPJ1
Find the selling price
Cost of the computer; $1,850.00
Markup: 75%
Answers
Answer:
2466.67
Step-by-step explanation:
1850/.75=2466.67
The cost of selling price of the computer is, $3,237.5
What is mean by Percentage?A number or ratio that can be expressed as a fraction of 100 or a relative value indicating hundredth part of any quantity is called percentage.
Given that;
Cost of the computer = $1,850.00
Markup = 75%
Now,
The cost of selling price of the computer is,
⇒ $1,850 + 75% of $1,850
⇒ $1850 + 75 /100 × $1850
⇒ $1850 + $1387.5
⇒ $3,237.5
Learn more about the percent visit:
https://brainly.com/question/24877689
#SPJ2