What is a group of objects that share common characteristics and are well-defined?
Answers
Answer:
The options as included in the attachment section are:
A. real numbers B.Cardinality C.element D.Set
The answer is D. Set
Step-by-step explanation:
In mathematics, a set is a group of well-defined objects that share common characteristics as rightly stated in this question. So in a mathematical calculation, the elements or objects collected as a group is called SET. The types of set include empty set, finite set, infinite set, universal set etc.
- Since set represents the whole collection or group, each object, which can be number, letter etc. in the group is an ELEMENT. Likewise, the cardinality of a set refers to the number of elements contained in a particular set.
Related Questions
At a hotel the surface of a swimming pool is modeled by the shape of the = Cross sections cut perpendicular to the y-axis are semi-circles I y is ellipse 9x^2+4y^2 =36 approximately how many cubie yards of water does this pool hold? measured in yards,
Answers
The shape of the swimming pool is modeled by the equation of an ellipse, given by 9\(x^{2}\) + 4\(y^{2}\) = 36. To find the volume, we integrate the area of each cross section over the range of y values that the ellipse covers.
The cross sections of the pool, cut perpendicular to the y-axis, are semi-circles. Since the cross sections are semi-circles, we know that the area of each cross section is (1/2) \(\pi\) \(r^{2}\), where r is the radius of the semi-circle. In this case, the radius of each semi-circle is given by the equation r = \(\sqrt{(9x^2 + 4y^2).}\) To find the limits of integration for y, we solve the equation of the ellipse for y:
\(9x^{2} +4y^{2}\) = 36
4\(y^{2}\) = 36 - 9\(x^{2}\)2
\(y^{2}\) =\(\frac{ 36 - 9x^{2} }{4}\)
y = ±\(\sqrt{\frac{(36 - 9x^2) }{4} }\)
Now we can integrate the area of each cross section from y = \(-\sqrt{\frac{ 36 - 9x^{2} }{4}}\) to y = \(\sqrt{\frac{ 36 - 9x^{2} }{4}}\)with respect to x, and multiply the result by 2 to account for the semi-circles on both sides of the y-axis. The integral of (1/2) π \((\sqrt{(9x^2 + 4y^2))} )^{2}\)with respect to x will give us the volume of water the pool can hold in cubic yards.
Learn more about Integration here:
https://brainly.com/question/30217024
#SPJ11
26=6(5-a)
What is a
Answers
Answer:
2/3
Step-by-step explanation:
Simplify
\(26=6\cdot \left(5-a\right)\\26=6\cdot 5+6\cdot -a\\26=30+6\cdot -a\\26=30+\left(6\cdot -1\right)a\\26=30-6a\\30-6a=26\)
Group constants
\(30-6a=26\\30-6a-30=26-30\\-6a+30-30=26-30\\-6a=26-30\\-6a=-4\\\)
Isolate the term, a
\(-6a=-4\\\frac{-6a}{-6}=\frac{-4}{-6}\\\frac{6a}{6}=\frac{-4}{-6}\\a=\frac{-4}{-6}\\\\\frac{-a}{-b} = \frac{a}{b}\\\\a=\frac{4}{6}\\a=\frac{2\cdot 2}{3\cdot 2}\\a=\frac{2}{3}\)
Which equations represent the line that is perpendicular to the line 5x − 2y = −6 and passes through the point (5, −4)? select three options. y = â€"two-fifthsx â€" 2 2x 5y = −10 2x − 5y = −10 y 4 = â€"two-fifths(x â€" 5) y â€" 4 = five-halves(x 5)
Answers
The equations that represent the line that is perpendicular to the line 5x - 2y = -6 and passes through the point (5, -4) are:
y + 4 = (-2/5)(x - 5)2x + 5y = -10y = (-2/5)x - 2
To find the equations that represent the line that is perpendicular to the line 5x - 2y = -6 and passes through the point (5, -4),
we first need to put the equation in slope-intercept form, y = mx + b.5x - 2y = -6-2y = -5x - 6y = 5/2 x + 3
The slope of the given line is 5/2.
To find the slope of the line perpendicular to this line, we can use the following formula:
slope of the perpendicular line = -1/m
where m is the slope of the given line.
So, the slope of the perpendicular line is:-1/(5/2) = -2/5
Thus, the equation of the line that is perpendicular to the given line and passes through the point (5, -4) is:
y - y_1 = m(x - x_1),
where m = -2/5, and
(x_1, y_1) = (5, -4).
y + 4 = (-2/5)(x - 5)
y + 4 = (-2/5)x + 2y = (-2/5)
x - 4 - 5y = 2x + 10y = (2/5)x - 4
Thus, the equations that represent the line that is perpendicular to the line 5x - 2y = -6 and passes through the point (5, -4) are:y + 4 = (-2/5)(x - 5)2x + 5y = -10y = (-2/5)x - 2
for such more question on perpendicular
https://brainly.com/question/1202004
#SPJ11
Your older brother drove to your grandparents’ house in a different car but left from the same location at the same time. If he traveled at a constant speed of 60 miles per hour, explain why he would reach your grandparents’ house first. Use words, diagrams, or numbers to explain your
Please answer I will mark brainlist
Answers
75m/60=1.25
1.25=1 1/4 hours
So the answer Is 1 1/4 hours.
hope this helps
Critically discuss how your organisation can utilise the balanced scorecard approach as a strategic control system used to ensure they are pursuing strategies that maximize long-term profitability
Answers
The balanced scorecard approach can be utilized as a strategic control system to ensure the organization pursues long-term profitability by aligning financial objectives with key performance indicators across multiple perspectives.
The balanced scorecard approach is a strategic control system that enables organizations to effectively measure and manage performance across various dimensions. It provides a holistic view of the organization's activities by incorporating financial and non-financial indicators, and it serves as a valuable tool to ensure strategies are aligned with long-term profitability goals.
One key aspect of the balanced scorecard approach is the inclusion of multiple perspectives. Instead of focusing solely on financial metrics, the balanced scorecard incorporates additional perspectives such as customer, internal processes, and learning and growth. This ensures a comprehensive evaluation of the organization's performance, taking into account both short-term financial results and the long-term drivers of profitability.
By utilizing the balanced scorecard approach, organizations can set clear objectives and identify relevant key performance indicators (KPIs) for each perspective. This allows for a more balanced and well-rounded assessment of performance, ensuring that strategies are not solely focused on financial outcomes but also consider customer satisfaction, operational efficiency, and employee development.
Furthermore, the balanced scorecard approach facilitates the translation of the organization's strategy into actionable initiatives. By establishing cause-and-effect relationships between the different perspectives, organizations can develop a clear understanding of how their strategic objectives will lead to long-term profitability. This enables better resource allocation, effective monitoring of progress, and timely adjustments to ensure strategies remain aligned with the pursuit of maximum profitability.
Learn more about balanced scorecard
brainly.com/question/31857420
#SPJ11
can you please answer this for me :
A
B
C
D

Answers
Answer:
17/21
Step-by-step explanation:
Because i had that question and it was 17/21
Find the first term and the common difference of the arithmetic
sequence whose 7th term is −17 and 20th term is −43
The first term is
The common difference is
Answers
The first term of the arithmetic sequence is -5. The common difference of the arithmetic sequence is -2.
In an arithmetic sequence, each term is obtained by adding a constant value, known as the common difference, to the previous term. To find the first term and the common difference, we can use the given information about the 7th and 20th terms.
Let's denote the first term as "a" and the common difference as "d". We are given that the 7th term is -17 and the 20th term is -43. Using this information, we can write the following equations:
For the 7th term: a + 6d = -17 (since the 7th term is obtained by adding 6d to the first term)
For the 20th term: a + 19d = -43 (since the 20th term is obtained by adding 19d to the first term)
To solve these equations, we can use a method such as substitution or elimination. Let's use the substitution method here.
From the first equation, we can express "a" in terms of "d":
a = -17 - 6d
Substituting this value of "a" into the second equation, we have:
(-17 - 6d) + 19d = -43
Simplifying the equation:
-17 + 13d = -43
13d = -26
d = -2
Now that we know the common difference "d" is -2, we can substitute it back into the first equation to find the first term "a":
a = -17 - 6(-2)
a = -17 + 12
a = -5
Therefore, the first term of the arithmetic sequence is -5 and the common difference is -2.
Learn more about arithmetic sequence here
https://brainly.com/question/6561461
#SPJ11
A basketball player makes a free throw 82.6% of the time. The player attempts 5 free throws. Use a histogram of the binomial distribution to determine what is the most likely outcome.
Answers
Answer:
The most likely outcome is exactly 4 free throws
Step-by-step explanation:
Given
\(n = 5\) --- attempts
\(p = 82.6\%\) ---- probability of a successful free throw
\(p = 0.826\)
Required
A histogram to show the most likely outcome
From the question, we understand that the distribution is binomial.
This is represented as:
\(P(X = x) = ^nC_x * p^x * (1 - p)^{n-x}\)
For x = 0 to 5, where x represents the number of free throws; we have:
\(P(X = x) = ^nC_x * p^x * (1 - p)^{n-x}\)
\(P(X = 0) = ^5C_0 * 0.826^0 * (1 - 0.826)^{5-0}\)
\(P(X = 0) = ^5C_0 * 0.826^0 * (0.174)^{5}\)
\(P(X = 0) = 1 * 1 * 0.000159 \approx 0.0002\)
\(P(X = 1) = ^5C_1 * 0.826^1 * (1 - 0.826)^{5-1}\)
\(P(X = 1) = ^5C_1 * 0.826^1 * (0.174)^4\)
\(P(X = 1) = 5 * 0.826 * 0.000917 \approx 0.0038\)
\(P(X = 2) = ^5C_2 * 0.826^2 * (1 - 0.826)^{5-2}\)
\(P(X = 2) = ^5C_2 * 0.826^2 * (0.174)^{3}\)
\(P(X = 2) = 10 * 0.682 * 0.005268 \approx 0.0359\)
\(P(X = 3) = ^5C_3 * 0.826^3 * (1 - 0.826)^{5-3}\)
\(P(X = 3) = ^5C_3 * 0.826^3 * (0.174)^2\)
\(P(X = 3) = 10 * 0.5636 * 0.030276 \approx 0.1706\)
\(P(X = 4) = ^5C_4 * 0.826^4 * (1 - 0.826)^{5-4}\)
\(P(X = 4) = 5 * 0.826^4 * (0.174)^1\)
\(P(X = 4) = 5 * 0.4655 * 0.174 \approx 0.4050\)
\(P(X = 5) = ^5C_5 * 0.826^5 * (1 - 0.826)^{5-5}\\\)
\(P(X = 5) = ^5C_5 * 0.826^5 * (0.174)^0\)
\(P(X = 5) = 1 * 0.3845 * 1 \approx 0.3845\)
From the above computations, we have:
\(P(X = 0) \approx 0.0002\)
\(P(X = 1) \approx 0.0038\)
\(P(X = 2) \approx 0.0359\)
\(P(X = 3) \approx 0.1706\)
\(P(X = 4) \approx 0.4050\)
\(P(X = 5) \approx 0.3845\)
See attachment for histogram
From the histogram, we can see that the most likely outcome is at: x = 4
Because it has the longest vertical bar (0.4050 or 40.5%)

Please help me with this math problem by showing a step-by-step explanation. I will give 25 points :D
Without graphing, classify each system of equations as independent, dependent, or inconsistent. Solve independent systems by graphing. 3=4y+x & 4y=−x+3
Answers
Step-by-step explanation:
3=4y+x => x+4y = 3
4y=−x+3 => x+4y = 3
the systems are dependent equations
Five years ago, someone used her $40,000 saving to make a down payment for a townhouse in RTP. The house is a three-bedroom townhouse and sold for $200,000 when she bought it. After paying down payment, she financed the house by borrowing a 30-year mortgage. Mortgage interest rate is 4.25%. Right after closing, she rent out the house for $1,800 per month. In addition to mortgage payment and rent revenue, she listed the following information so as to figure out investment return: 1. HOA fee is $75 per month and due at end of each year 2. Property tax and insurance together are 3% of house value 3. She has to pay 10% of rent revenue for an agent who manages her renting regularly 4. Her personal income tax rate is 20%. While rent revenue is taxable, the mortgage interest is tax deductible. She has to make the mortgage amortization table to figure out how much interest she paid each year 5. In last five years, the market value of the house has increased by 4.8% per year 6. If she wants to sell the house today, the total transaction cost will be 5% of selling price Given the above information, please calculate the internal rate of return (IRR) of this investment in house
Can you show the math as far as formulas go?
Answers
Given the following information: Five years ago, someone used her $40,000 saving to make a down payment for a townhouse in RTP. The house is a three-bedroom townhouse and sold for $200,000 when she bought it. After paying down payment, she financed the house by borrowing a 30-year mortgage.
Mortgage interest rate is 4.25%. Right after closing, she rent out the house for $1,800 per month. In addition to mortgage payment and rent revenue, she listed the following information so as to figure out investment return: 1. HOA fee is $75 per month and due at end of each year 2. Property tax and insurance together are 3% of house value 3. She has to pay 10% of rent revenue for an agent who manages her renting regularly 4. Her personal income tax rate is 20%. While rent revenue is taxable, the mortgage interest is tax deductible. She has to make the mortgage amortization table to figure out how much interest she paid each year 5. In the last five years, the market value of the house has increased by 4.8% per year 6.
To know more about interest visit:
https://brainly.com/question/30393144
#SPJ11
In 2005, there were 1000 rabbits on an island. The population grows 8% per year. AT this rate, how many
rabbits will there be on the island by 2020?
Answers
Answer: 3172
Step-by-step explanation:
The equation of the line tangent to the differentiable and invertible function f(x) at the point (-1,3) is given by y = –2x + 1. Find the equation of the tangent line to f-1(x) at the point (3, -1).
Answers
The equation of the tangent line to f-1(x) at the point (3, -1) is y = 1/(-2) x - 1/2.
This is because the slope of the tangent line to f(x) at (-1,3) is -2, and since f(x) and f-1(x) are inverse functions, the slopes of their tangent lines are reciprocals.
Therefore, the slope of the tangent line to f-1(x) at (3,-1) is -1/2. To find the y-intercept, we can use the fact that the point (3,-1) is on the tangent line. Plugging in x=3 and y=-1 into the equation y = -1/2 x + b, we get b = 1/2. Therefore, the equation of the tangent line to f-1(x) at (3,-1) is y = 1/(-2) x - 1/2.
In summary, to find the equation of the tangent line to f-1(x) at a point (a,b), we first find the point (c,d) on the graph of f(x) that corresponds to (a,b) under the inverse function.
Then, we find the slope of the tangent line to f(x) at (c,d), take the reciprocal, and plug it into the point-slope formula to find the equation of the tangent line to f-1(x) at (a,b).
To know more about tangent line click on below link:
https://brainly.com/question/31326507#
#SPJ11
PLEASE HELPP IM TIMED I'LL DIE I'LL GIVE BRAINLIEST AND 50 POINTSSS
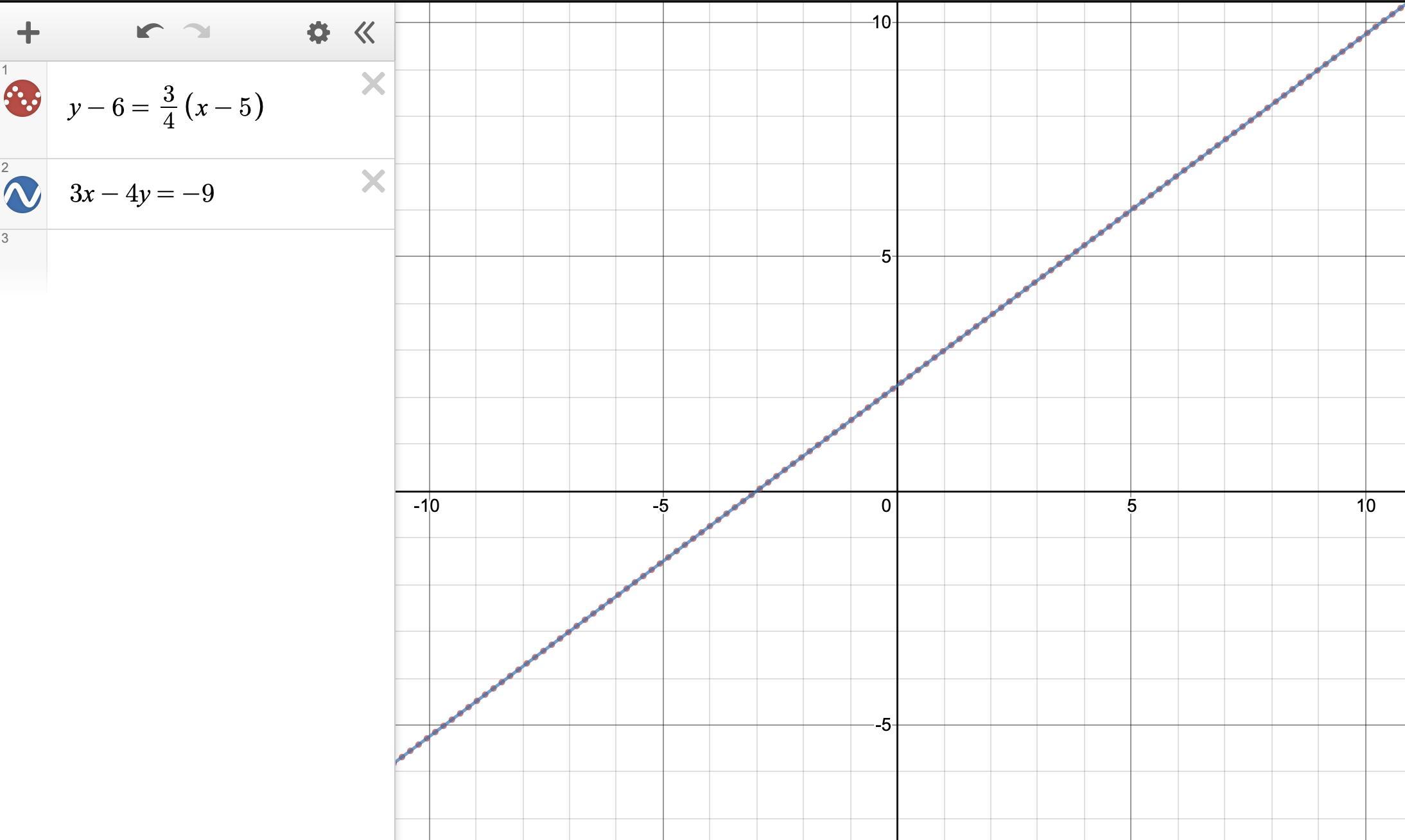
Write the standard form of the equation y−6=3/4(x−5).
Answers
9514 1404 393
Answer:
3x -4y = -9
Step-by-step explanation:
Multiply by 4 to clear the fraction.
4(y -6) = 3(x -5)
Subtract the left-side term to get variables on the same side, with a positive x-coefficient.
0 = 3(x -5) -4(y -6)
Eliminate parentheses and collect terms.
0 = 3x -15 -4y +24
0 = 3x -4y +9
Subtract 9 and swap sides to get standard form.
3x -4y = -9
_____
Standard form is ...
ax +by = c
where a ≥ 0, and a, b, c are mutually prime integers. If a=0, then b > 0.
__
The attached graph shows the equations give the same line. The original line is shown dotted so that you can see they overlap.
Find f. f ''(theta) = sin(theta) + cos(theta), f(0) = 4, f '(0) = 1
Answers
The function f(theta) is:
f(theta) = sin(theta) + cos(theta) + 3
To find the function f, we will integrate the given second derivative with respect to theta twice, and use the initial conditions to determine the constants of integration.
First, integrating f ''(theta) = sin(theta) + cos(theta) with respect to theta gives:
f '(theta) = -cos(theta) + sin(theta) + C1
where C1 is a constant of integration.
Next, integrating f '(theta) = -cos(theta) + sin(theta) + C1 with respect to theta gives:
f(theta) = sin(theta) + cos(theta) + C1*theta + C2
where C2 is another constant of integration.
To determine the values of C1 and C2, we use the initial conditions:
f(0) = 4 gives us:
4 = sin(0) + cos(0) + C1*0 + C2
4 = 1 + C2
so C2 = 3.
f '(0) = 1 gives us:
1 = -cos(0) + sin(0) + C1
1 = 1 + C1
so C1 = 0.
Therefore, the function f(theta) is:
f(theta) = sin(theta) + cos(theta) + 3
Note that there are other ways to express this function, such as using trigonometric identities to simplify the expression, but this is the most general form.
To learn more about integration, refer below:
https://brainly.com/question/30900582
#SPJ11
The sum of the ages of a father and son is 45 years. Five years ago, the product of their ages was four times the fathers age at that time. What is the present ages of father and son?.
Answers
The present ages of the father and son are 36 and 9, respectively.
The sum of the ages of a father and son is 45 years. Five years ago, the product of their ages was four times the father's age at that time. To find the present ages of the father and son, we can set up a system of equations.
Let's denote the present ages of the father as "F" and the present age of the son as "S".
From the information given, we have two equations:
Equation 1: F + S = 45 (The sum of their ages is 45)
Equation 2: (F - 5)(S - 5) = 4(F - 5) (Five years ago, the product of their ages was four times the father's age at that time)
To solve this system of equations, we can use substitution or elimination method.
Let's solve it using the substitution method:
From Equation 1, we can express F in terms of S: F = 45 - S
Now, substitute F in Equation 2 with 45 - S:
(45 - S - 5)(S - 5) = 4(45 - S - 5)
Simplify the equation:
(40 - S)(S - 5) = 4(40 - S)
Expand and simplify:
40S - 5S - 200 + 25 = 160 - 4S
Combine like terms:
35S - 175 = 160 - 4S
Add 4S to both sides:
35S + 4S - 175 = 160
Combine like terms:
39S - 175 = 160
Add 175 to both sides:
39S = 335
Divide both sides by 39:
S = 335/39
Simplify:
S ≈ 8.59
Since age cannot be in decimal places, we can approximate the son's age to the nearest whole number:
S ≈ 9
Now, substitute S = 9 into Equation 1 to find the father's age:
F + 9 = 45
Subtract 9 from both sides:
F = 45 - 9
F = 36
Therefore, the present ages of the father and son are 36 and 9, respectively.
Learn more about present ages https://brainly.com/question/20034121
#SPJ11
if a > b, under what condition is | - | = a - b?
Answers
If a > b, then |a - b| = a - b if a - b is positive. This means that the distance from a - b to zero on the number line is equal to a - b itself. If a - b is negative, then |a - b| is equal to the opposite of a - b.
The absolute value of a - b is equal to a - b if a - b is positive because the absolute value of a number is the distance from that number to zero on the number line. So, if a is greater than b, then a - b is a positive number. Therefore, the distance from a - b to zero on the number line is equal to a - b.
The absolute value of a number is the distance from that number to zero on the number line. For example, the absolute value of 5 is 5 because the distance from 5 to 0 on the number line is 5 units. The absolute value of -5 is also 5 because the distance from -5 to 0 on the number line is also 5 units.
Now, let's look at the expression |a - b|. This means the absolute value of the difference between a and b. If a is greater than b, then a - b is a positive number. For example, if a = 10 and b = 5, then a - b = 5. So, |a - b| = |10 - 5| = |5| = 5.
However, we are looking for the condition under which |a - b| = a - b. This means that the absolute value of a - b is equal to a - b itself. This only happens when a - b is positive. Let's use the same example as before. If a = 10 and b = 5, then a - b = 5. In this case, a - b is positive, so |a - b| = |10 - 5| = |5| = 5, which is equal to a - b.
To know more about distance visit :-
https://brainly.com/question/13034462
#SPJ11
in a school there are 16 teachers and 220 students. of these students 120 are girls and 100 are boys.
one teacher, one girl, and one boy are going to be chosen to represent the school.
work out the number of different ways there are to choose one teacher, one girl and one boy.
Answers
The requried there are 192,000 different ways to choose one teacher, one girl, and one boy to represent the school.
What are permutation and combination?In arithmetic, combination and permutation are two different ways of grouping elements of a set into subsets. In combination, the components of the subset can be recorded in any order. In a permutation, the components of the subset are listed in a distinctive order.
Here,
To work out the number of different ways to choose one teacher, one girl, and one boy, we can use the multiplication principle of counting.
First, we need to choose one teacher out of 16. This can be done in 16 ways. Next, we need to choose one girl out of 120. This can be done in 120 ways. Finally, we need to choose one boy out of 100. This can be done in 100 ways.
By the multiplication principle of counting, the total number of ways to choose one teacher, one girl, and one boy is,
16 × 120 × 100 = 192,000
Therefore, there are 192,000 different ways to choose one teacher, one girl, and one boy to represent the school.
Learn more about permutations and combinations here: https://brainly.com/question/2295036
#SPJ9
plz help me with this math question
3 more questions to do

Answers
Answer:
1308
Step-by-step explanation:
PEMDAS has us do 6^4 first which is 1296. Then we can do 6*2 which is 12 then 12 + 1296 is 1308.
Find 3 consecutive odd integers with a sum of 63. PLEASE HELP!!!
Answers
Answer:
the numbers are 20, 21 and 22
Step-by-step explanation:
x+(x+1) + (x+2) = 63
3x +3 = 63
3x = 60
x = 20
doing this for ponits
Answer:
the numbers are 20, 21 and 22
Step-by-step explanation:
x+(x+1) + (x+2) = 63
3x +3 = 63
3x = 60
x = 20
a) 2.5x + 1.25 < 3.75
b)5.12 2.4x + 0.3
help!!!
Answers
Answer:
a) 1
b)I would like to help u but i don't understand the question I think something is missing there plus sign or minus sign sry
Step-by-step explanation:
2.5x + 1.25 < 3.75
2.5x < 3.75 - 1.25
2.5x < 2.5
\( \frac{2.5x}{2.5} = \frac{2.5}{2.5} \)
x = 1
I hope u like it ❤️❤️
For any question comment me
Really sorry for the second question
Multiply 422 x 18 using the standard algorith
Answers
Answer:
Actually...It's really easy
Step-by-step explanation:
All you have to do is put the numbers in order like this
422
x 18
_________________
7,596
There you go! Hope it helps!
The first two numbers in a sequence h are h(1)=2 and h(2)=6
If h is an arithmetic sequence, write a definition for the nth term of h explain or show your reasoning.
Answers
An arithmetic sequence is a sequence of integers with its adjacent terms differing with one common difference. The nth term of the arithmetic series can be defined as hₙ = 4n - 2.
What is an arithmetic sequence?An arithmetic sequence is a sequence of integers with its adjacent terms differing with one common difference.
If the initial term of a sequence is 'a' and the common difference is of 'd', then we have the arithmetic sequence as:
a, a + d, a + 2d, ... , a + (n+1)d, ...
The nth term of an arithmetic sequence is given by the formula,
aₙ = a₁ + (n-1)d
Since the first term of the arithmetic sequence is 2, while the difference is 4. Therefore, the definition for the nth term of arithmetic sequence,h can be written as,
hₙ = 2 + (n-1)4
hₙ = 2 + 4n -4
hₙ = 4n - 2
Hence, the nth term of the arithmetic series can be defined as hₙ = 4n - 2.
Learn more about Arithmetic Sequence:
https://brainly.com/question/3702506
#SPJ1
A scale drawing of a rectangular park had a scale of 1 cm = 60 m
What is the actual perimeter of the park in meters?

Answers
Answer:
Solution
1cm=60 cm
4.5cm=4.5×60
=270m (breadth)
3.7cm=3.7×60
=222m (length)
Perimeter of rectangle=2(l+b)
=2(222+270)
=2×492
=984m
hope it helps you
make me brainliest if u r satisfied
The perimeter of the rectangular park is P = 984 m
What is the Perimeter of a Rectangle?The perimeter P of a rectangle is given by the formula, P=2 ( L + W) , where L is the length and W is the width of the rectangle.
Perimeter P of rectangle = 2 ( Length + Width )
Given data ,
Let the scale of the rectangular park be 1 cm = 60m
Now , the Perimeter P of rectangle = 2 ( Length + Width )
The length of the rectangular park L = 4.5 cm = 4.5 x ( 60 )
The length of the rectangular park L = 270 m
And ,
The width of the rectangular park W = 3.7 cm = 3.7 x ( 60 )
The width of the rectangular park W = 222 m
Now , the perimeter of rectangular park = 2 ( 270 + 222 )
The perimeter of rectangular park P = 984 m
Hence , the perimeter of the rectangular park is 984 m
To learn more about perimeter of rectangle click :
https://brainly.com/question/15725265
#SPJ2
What is 42/77 in simplest form?
4/7
6/11
7/11
6/7

Answers
Steps to simplifying fractions
Find the GCD (or HCF) of numerator and denominator
GCD of 42 and 77 is 7
Divide both the numerator and denominator by the GCD
42 ÷ 7
77 ÷ 7
Reduced fraction:
6
11
Therefore, 42/77 simplified to lowest terms is 6/11.
Find the measure of line BD.

Answers
Answer:
Step-by-step explanation:
BD is geometric mean
BD² = 5 × 13 = 65
BD = √65
The Water Department checks the city water supply on a regular basis for
contaminants such as trihalomethanes (THMs). The Water Department takes
200 samples and estimates that the concentration of THMs in your drinking
water is 3 ppb (parts per billion), with a standard deviation of 0. 3 ppb.
Assuming the samples were random and unbiased, how much confidence
can you have in this data?
Answers
We can be 95% confident that the true mean concentration of THMs in your drinking water lies within the range [2.9584 ppb, 3.0416 ppb]. This was calculated using a confidence interval formula for the mean.
The confidence interval for the mean concentration of THMs can be calculated using the formula x ± z * (s/√n), where x is the sample mean, z is the z-score for a given confidence level, s is the sample standard deviation and n is the sample size.
In this case, we have x = 3 ppb, s = 0.3 ppb, and n = 200. To calculate the confidence interval at a certain confidence level (e.g. 95%), we need to find the corresponding z-score. For a 95% confidence level, the z-score is approximately 1.96.
Substituting these values into the formula above gives us:
3 ± 1.96 * (0.3/√200) = [2.9584, 3.0416]
So we can be 95% confident that the true mean concentration of THMs in your drinking water lies within the range [2.9584 ppb, 3.0416 ppb].
Learn more about confidence interval here: brainly.com/question/24131141
#SPJ4
A regular pentagon is inscribed in a circle as shown. 1. Find the measure of minor arc cut off by one of the diagonals.2. Find the length of the same minor arc in problem 16a, given the radius of the circle is 10 cm. Leave the answer is terms of pi.

Answers
SOLUTION:
Step 1:
we are to find the measure of minor arc cut off by one of the diagonals;
The sum of interior angles in a pentagon is:
\(\begin{gathered} (n-2)\text{ x 180} \\ (5-2)\text{ x 180} \\ 3\text{ x 180} \\ 540 \end{gathered}\)Each interior angle of a regular pentagon is
\(\frac{540}{5}\text{ = 108}\)So the size of the major arc can be gotten by the circle theorem; the angle at the centre is twice the angle at the circumference.
\(\text{The major arc = 2 x 108 = 216}\)Then recall,
\(\begin{gathered} \text{The major arc + the minor arc = 360 (sum of angles at a point)} \\ 216\text{ + the minor arc = 360} \\ \text{The minor arc = 360 - 216} \\ \text{The minor arc =144} \end{gathered}\)Step 2:
We are to find the length of the same minor arc in problem;
\(\frac{\theta}{360}\text{ x 2 }\pi\text{ r}\)Where our angle (titan) is 144 and radius is 10
\(\begin{gathered} \frac{144}{360}\text{ x 2 x }\pi\text{ x 10} \\ \\ 8\pi \end{gathered}\)So the length of the minor arc, given that the radius is 10 cm is 8 pi
The figure shown has a total area of 168 cm².
Which equation can be used to find
the value of a?
168 18 12 + 2x x
168 = 18 x+12 2x
168 18 + 12-3x
168 18 3z + 12 2x
18 cm
x cm
2x cm
12 cm

Answers
Answer:
Second option 168= 18.X + 12.2X
Step-by-step explanation:
Area of the shape is in two parts,
Are of the larger rectangle is Lenght x width
Lenght is 12cm and width is x +2x
Area = 12 x 3x = 36x cm²
Area of the smaller rectangle = 6 x X = 6xcm²
Total area 36x + 6x = 168cm²
Another method
Find the area of the big rectangle including the cut off area
Lenght x width = 18 x (2x + X)
Area =18 x 3x or 18.3x
Calculate the white area
Length x width = 6 x 2x = 12x
Deduct the white area from the larger area
168= 18.3x - 12x
Third method
Divide the rectangle from top down
First rectangle length x width = 18x X or 18x
Second rectangle length x width = 12 x 2x
168= 18. x + 12 . 2x
The correct equation which can be used to find the value of x is,
⇒ 168 = 18 × x + 12 × 2x
What is mean by Rectangle?A rectangle is a two dimension figure with 4 sides, 4 corners and 4 right angles. The opposite sides of the rectangle are equal and parallel to each other.
Given that;
The figure shown has a total area of 168 cm².
Now, We can find as;
Area of rectangle = Length x width
Hence, We can formulate;
⇒ 18 × x + 12 × 2x = 168
Thus, The correct equation which can be used to find the value of x is,
⇒ 168 = 18 × x + 12 × 2x
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ5
Find the value of the variable x. If your answer is not an integer, write it in simplest radical form with
the denominator rationalized

Answers
The values of the variable are:
x is 45.
y is 18.
z is 18.
What are trigonometric identities?There are three commonly used trigonometric identities.
Sin x = Perpendicular / Hypotenuse
Cosec = Hypotenuse / Perpendicular
Cos x = Base / Hypotenuse
Sec x = Hypotenuse / Base
Tan x = Perpendicular / Base
Cot x = Base / Perpendicular
We have,
From the figure,
Sin 45 = z / (18√2)
Sin 45 = 1 /√2
So,
1/√2 =z / 18√2
z = 18
Cos 45 = y / (18√2)
1/√2 = y/18√2
y = 18
Tan x = y / z
Tan x = 18/18
Tan x = 1
x = \(tan^{-1}\)1
x = \(tan^{-1}\) tan 45
x = 45
Thus,
x is 45.
y is 18.
z is 18.
Learn more about trigonometric identities here:
https://brainly.com/question/14746686
#SPJ1
the train that left boise at 9:23 pulled only potato cars and lumber cars in the ratio of 23:9. if there were 72 lumber cars how many cars in total did the train pull
Answers
Answer:
256
Step-by-step explanation:
23:9
9x8=72
23x9=184
184+72
It says in total