What is 3 + 1
What is it
Answers
uh it's 4 yes. the answer would be 4
Answer:
it's 4
hope it is helpful to you
Related Questions
6.) The average delivery charge for a refrigerator is $54. The standard deviation is 53. Find the
range in which at least 75% of the data values will fall.
1
Answers
Answer:
88.9%
Step-by-step explanation:
Using the invNorm function on the calculator, the range of 75% of the data values is $-6.97 to $114.96. In stats, not everything makes sense.
To use the invNorm function, go to 2nd vars, invNorm. Put .75 in the area, 54 in the mean, and 53 in the standard deviation.
Solve for x. 7.5x/11=4.8/5
Answers
The value of the variable is 1. 40
How to determine the valuewe need to know that algebraic expressions are described as expressions that are made up of term, variables, constants, factors and coefficients.
these algebraic expressions are also made up of arithmetic operations.
These arithmetic operations are listed as;
BracketDivisionAdditionSubtractionMultiplicationParenthesesFrom the information given, we have that;
7.5x/11=4.8/5
cross multiply the values, we get;
7.5x(5) = 4.8(11)
multiply the values
37. 5x = 52. 8
Divide both sides by the coefficient of x, we get;
x = 1. 40
Learn about algebraic expressions at: https://brainly.com/question/4541471
#SPJ1
Why early math is just as important as early reading
Answers
Answer:
Early math is just as important as early literacy; in fact, it can improve reading and writing skills. Kids who start with numerical skills even in infancy will do better with math when they reach school.
Let the random variable Q represent the number of students who go to a certain teacher office hour each day. The standard deviation of Q is 2.2. Which of the following is the best interpretation of the standard deviation?
a. On average, the number of students going to an office hour varies from the mean by about 2.2 students.
b. For a randomly selected office hour, the number of students who will go is 2.2.
с. For a randomly selected office hour, the number of students expected to go will vary from the mean by 2.2 students.
d. For a random selection of office hours, the average number of students expected to go is 2.2.
e. For a random selection of office hours, the E average number of students expected to go will vary from the mean by 2.2 students.
Answers
Answer:
A: On average, the number of students going to an office hour varies from the mean by about 2.2 students.
Step-by-step explanation:
We are given that:
- Random variable Q is used to represent the number of students who go to a certain teachers office hour each day.
-The standard deviation of Q is 2.2.
Now, standard deviation in relation to mean is defined as the statistic that measures the dispersion of a set of data relative to its mean.
Applying that definition to the question means that the number of students on the average varies from the mean by 2.2.
Thus, option A is correct.
Answer:
A: On average, the number of students going to an office hour varies from the mean by about 2.2 students.
Step-by-step explanation:
I second the person below me i got it right on asigmnemnt
If a ring costs a jeweler $2100, at what price should it be sold to yield a profit of 50% on the selling price?
Answers
2100/2 = 1050
Meaning 50% is $1050
gdsgdsgdsgdsgdsgdsgdsgdsgdsgdsgdsgdsgdsgdsgdsgds
Answers
Answer:
hi thank u for the free point
Find the slope.
y= X/3 + 4
M= ?/?
Answers
Answer:
m=1/7
Step-by-step explanation:
The slope of y=x/3 + 4 is 1/7.
x/3+4 = x/7 so m = 1/7.
Answer:
m = 1/3
Step-by-step explanation:
The equation given is in slope-intercept form, which has the basic structure:
y = mx + b
In this equation, "m" is the slope and "b" is the y-intercept.
The value of "b" is 4.
The value of "m" is 1/3. This is because (x/3) is the same as (1/3 times x).
11 less than the quotient of
4
44 and
�
xx.
Answers
The expression which is used to represents the statement "one-more than the quotient of a number x" and 4 is "x/4 + 1".
A "Quotient" is the result of a division operation between two numbers, where one number is divided by another. It represents the number of times one number is contained within another number.
An "Expression" is defined as "mathematical-phrase" which contain numbers, variables, and operators such as addition, subtraction, multiplication, and division. It can also contain functions and other mathematical symbols.
The quotient of a number"x" and 4 can be written as x/4.
So, one more than the quotient of a number x and 4 can be represented by the expression:
⇒ x/4 + 1,
Therefore, required mathematical expression is "x/4 + 1".
Learn more about Expression here
https://brainly.com/question/30553495
#SPJ1
The given question is incomplete, the complete question is
Write an expression to represent : One more than the quotient of a number x and 4.
Find tan(B) in the triangle.

Answers
Step-by-step explanation:
tan = perpendicular / base
acc. to diagram ,
angle C = 90°
such that
AB is hypotenuse
acc to theta ,
AC is perpendicular and BC is base
therefore
tan theta = AC / BC
tan theta = 8/15
Assume that any variable exponents represent whole numbers. Factor the greatest common factor from the polynomial.
Answers
Question:
Assume that any variable exponents represent whole numbers. Factor the greatest common factor from the polynomial.
\(9x^4 -6x^2\)
Answer:
\(3x^2(3x^2 -2)\)
Step-by-step explanation:
Given
\(9x^4 -6x^2\)
Required
Factorize
\(9x^4 -6x^2\)
Express 9 as 3 * 3 and 6 as 3 * 2
\(3 * 3x^4 -3 * 2x^2\)
Factorize 3 from both terms
\(3(3x^4 -2x^2)\)
Express x^4 as x^2 * x^2
\(3(3x^2 * x^2 -2x^2)\)
Factorize x^2 from both terms
\(3x^2(3x^2 -2)\)
Hence, the factors of \(9x^4 -6x^2\) are
\(3x^2\) and \(3x^2 - 2\)
Given that f(x) = x + 4 and g(x) = x + 7, find (g - 4(x).
Answers
Answer: The value of \((g - f)(x)=4 .\)
Step-by-step explanation:
Given functions : \(f(x) = x + 4\) and \(g(x) = x + 7\)
To find : \((g - f)(x)\)
Difference between two functions: \((u-v)(x)=u(x)-v(x)\)
Then, \((g-f)(x)=g(x)-f(x)\)
\(=(x+7)-(x+4)=x+7-x-4\\\\=7-4=3\)
Hence, the value of \((g - f)(x)=4 .\)
Which of the following are solutions to the inequality below? Select all that apply. 89 < 12 h
Answers
Answer:
7.4 < h
Step-by-step explanation:
89 < 12h
Divided both sides by 12
7.4 < h
The answer is:
⇨ h > 7.417Work/explanation:
The objective of this problem is to isolate the variable. So in the inequality \(\bf{89 < 12h}\), we should isolate h.
So I divide each side by 12
\(\bf{7.417 < h}\)
Hence, h > 7.417Mr. Lewis is 63 years old. He wants to take out a five-year level-term life insurance
policy with a face value $700,000. The monthly premium is $72.
2. If he dies after paying for the policy for 24 months, how much will the insurance
company pay his beneficiaries?
Answers
The amount insurance company will pay is $700000.
We are given that
Age of Mr. lewis= 63
Policy value= $700,000
Now,
If Mr. Lewis dies after paying for the policy for 24 months, he would have paid a total of 24 * $72 = $1728 in premiums. Since he has a five-year level-term life insurance policy with a face value of $700,000, his beneficiaries would receive the full face value of the policy if he dies within the five-year term.
Therefore, by algebra the answer will be $700000.
More about the Algebra link is given below.
brainly.com/question/953809
#SPJ1
Can you please help me
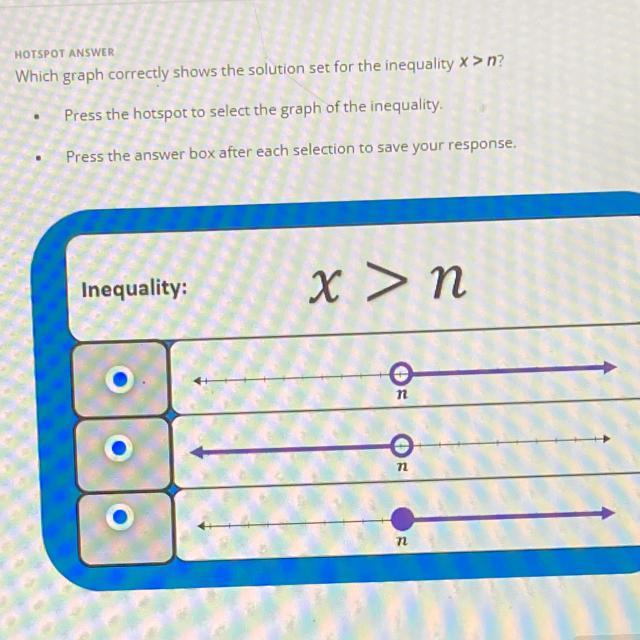
Answers
Answer:
first graph
Step-by-step explanation:
x > n
the graph will have an open circle at the value n , indicating that x cannot equal n ( note solid circle if x ≥ n )
the arrow from n will point in the right direction, indicating values of x greater than n.
the graph representing x > n is the first graph
when I asked to factor the trinomial, 4x^2 + 12x + 9, A student gives the answer (2x-3)(2x-3). what is the one thing wrong with this answer?

Answers
Given the following trinomial expression:
\(4x^2+12x+9\)The given expression is a complete square.
the factor of the given trinomial will be as follows:
\(4x^2+12x+9=(2x+3)(2x+3)\)A student gives the answer (2x-3)(2x-3).
So, by comparing the student's answer to our answer, we can note the student is wrong in the sign
So, the answer will be:
C. The minus signs should be plus signs
A lab technician mixes a 10% acid solution with a 50% acid solution to create 40 ml of a 40%
solution. How much of each solution must be used?
Answers
Answer:
10 ml of 10%
30 ml of 50%
Step-by-step explanation:
x = amount of 10%
40 - x = amount of 50%
-------------------------------------
10x + 50(40 - x) = 40(40)
10x + 2000 - 50x = 1600
-40x + 2000 = 1600
-40x = -400
x = 10 ml of 10%
40 - x = 30 ml of 50%
Which of the following functions is graphed below?86a.-82468-6-4-20-2-46-81x2 +2. x<1O A.y-1-x+2, X21O B. v- {**+2.x211-x+ 2 x 1O c. v - (x + 2 x 51|-x+2, *> 1D. y - {**+2x > 1|-*+2, 21

Answers
The circles bounding a graph can tell us the boundary of the graph, based on its shading or lack thereof.
If the circle is shaded, the position of the circle is included in the graph, that is:
\(\begin{gathered} x\ge c\text{ }or\text{ }x\le c \\ \text{where} \\ c=\text{ Location of the circle} \end{gathered}\)If the circle is unshaded, the position of the circle is not included in the graph, that is:
\(\begin{gathered} x>c\text{ }or\text{ }xThe two functions from the options are:
\(\begin{gathered} y=x^2+2 \\ \text{and} \\ y=-x+2 \end{gathered}\)The quadratic graph is bounded by an unshaded circle at x = 1. Since the graph is plotted at x < 1, then the function and its boundary are:
\(y=x^2+2,x<1\)The linear graph is bounded by a shaded circle at x = 1. Since the graph is plotted at x > 1, then the function and its boundary are:
\(y=-x+2,x\ge1\)Therefore, the correct option is OPTION A.
f(x)=1/3x g(x)= 1/3x f(g(x))= Are they inverses? Please explain.
Answers
Answer:
no
Step-by-step explanation:
f(g(x))= x if they are inverses
(x)=1/3x
g(x)= 1/3x
f(g(x)) = 1/3 (g(x) = 1/3 (1/3x) = 1/9x
This is not x so they are not inverse functions
A population of rare birds in town is currently listed at 2,000. It is declining at a rate of 2% per year. How many birds will be left after 20 years? Round your answer to the nearest whole number.
A. 1,335 birds
B. 1,980 birds
C. 2,972 birds
D. 23 birds
Answers
Option(A) is the correct answer is A. 1,335 birds.
To calculate the number of birds that will be left after 20 years, we need to consider the annual decline rate of 2%.
We can use the formula for exponential decay:
N = N₀ * (1 - r/100)^t
Where:
N is the final number of birds after t years
N₀ is the initial number of birds (2,000 in this case)
r is the annual decline rate (2% or 0.02)
t is the number of years (20 in this case)
Plugging in the values, we get:
N = 2,000 * (1 - 0.02)^20
N = 2,000 * (0.98)^20
N ≈ 2,000 * 0.672749
N ≈ 1,345.498
Rounded to the nearest whole number, the number of birds that will be left after 20 years is 1,345.
for similar questions on population.
https://brainly.com/question/30396931
#SPJ8
A box contains 54 coins which are either 20-cent coins or 50-cent coins. If the total value of all the coins is $20.70, find the number of 20-cent coins in the box. LOF 1 11.
Answers
Number of 20-cent coins in the box are 33.
1. Let's assume the number of 20-cent coins to be x and the number of 50-cent coins to be y.
2. We can set up two equations based on the given information:
- x + y = 54 (since the total number of coins in the box is 54)
- 0.20x + 0.50y = 20.70 (since the total value of all the coins is $20.70)
3. We can multiply the second equation by 100 to get rid of the decimals:
- 20x + 50y = 2070
4. Now, we can use the first equation to express y in terms of x:
- y = 54 - x
5. Substitute the value of y in the second equation:
- 20x + 50(54 - x) = 2070
6. Simplify and solve for x:
- 20x + 2700 - 50x = 2070
- -30x = -630
- x = 21
7. Substituting the value of x back into the first equation:
- 21 + y = 54
- y = 33
8. Therefore, there are 21 20-cent coins and 33 50-cent coins in the box.
For more such questions on Number, click on:
https://brainly.com/question/30752681
#SPJ8
Graph the system of inequalities. Then use your graph to identify the point that
represents a solution to the system.
x + y2 3
x-3y< 2
(6, 1)
(8,-1)
(6,2)
O (6,-2)
Answers
The coordinates in the solution to the systems of inequalities graphically is (6, 2)
Solving the systems of inequalities graphicallyFrom the question, we have the following parameters that can be used in our computation:
x + y > 3
x - 3y < 2
Next, we plot the graph of the system of the inequalities
See attachment for the graph
From the graph, we have solution to the system to be the shaded region
The coordinates in the solution to the systems of inequalities graphically is (6, 2)
Read more about inequalities at
brainly.com/question/30977554
#SPJ1

=
Write an exponential function y = abx whose
graph passes through the points (1,6), (2, 18)
Answers
Answer:
\(2(3) {}^{x} \)
Step-by-step explanation:
\(y = ab {}^{x} \)
We know that when x=1, y=6
\(6 = a {b}^{1} \)
x=2, y=18
\(18 = a {b}^{2} \)
Notice that if we divide
\( \frac{ {ab}^{2} }{ab} = b\)
So if we divide 18 and 6, that will give us our common ratio.
\( \frac{18}{6} = 3\)
So our common ratio is 3.
So know we have
\(a(3) {}^{x} \)
Plug in one of the points to find a.
\(6 = a(3)\)
\(a = 2\)
So the equation. we have
\(2 \times ({3}^{x} )\)
3.12x3.6
what is the answer?
Answers
Answer:
11.232
Step-by-step explanation:
3.12 × 3.6 is 11.232
Solve the following for θ, in radians, where 0≤θ<2π.
3cos2(θ)+6cos(θ)−4=0
Answers
Answer:
0 ≤ < 2
Step-by-step explanation:
Answer:1.02 5.27 are correct
Step-by-step explanation:We can solve this quadratic equation in cos(θ) by using the substitution u = cos(θ):
3u^2 + 6u - 4 = 0
Now we can use the quadratic formula to solve for u:
u = (-b ± sqrt(b^2 - 4ac)) / 2a
where a = 3, b = 6, and c = -4. Substituting these values, we get:
u = (-6 ± sqrt(6^2 - 4(3)(-4))) / 2(3)
u = (-6 ± sqrt(84)) / 6
u = (-3 ± sqrt(21)) / 3
Therefore, either:
Name the property illustrated If g = 3h and 3h = 16, then g = 16
3
Answers
The property illustrated ca be classified as the transitive property of equality
Transitive property of equalityEquation are expressions separated by an equal sign. For transitive property, if two system of equation are equal, and the first is equal to the second, then they 2nd is equal to the third, they are transitive.
According to the transitive property of equality, two quantities that are equal to the same thing are equal to each other. For instance If x = 10 and 10 = y, then x = y.
Given that g = 3h and 3h = 16, then g = 16, then the property illustrated ca be classified as the transitive property of equality
Learn more on transitive property here: https://brainly.com/question/4083674
#SPJ1
If u get this right u get branlnest

Answers
Answer:
Option 4
Step-by-step explanation:
\(2(a+6)\)
Substitute \(a=2\):
\(2(2+6)=2(8)=16\)
-------------------------------
Check first option:
\(4a+8\)
Substitute \(a=2\):
\(4(2)+8=8+8=16\)
Since 16 is not greater than 16, the first option is incorrect.
-------------------------------------------------------------------------------------
Check second option:
\(2a+a^2\)
Substitute \(a=2\):
\(2(2)+2^{2} =4+4=8\)
Since 8 is not greater than 16, the second option is incorrect.
-------------------------------------------------------------------------------------
Check third option:
\(2a+12\)
Substitute \(a=2\):
\(2(2)+12=4+12=16\)
Since 16 is not greater than 16, the third option is incorrect.
-------------------------------------------------------------------------------------
Check fourth option:
\(a^4+2\)
Substitute \(a=2\):
\(2^4+2=16+2=18\)
Since 18 is greater than 16, the fourth option is correct.
Antonio needs 3.5 liters of water for an experiment.
He has 1.375 liters.
How much more water does Antonio need?
Answers
Answer:
2.125
Step-by-step explanation:
3.5-1.375=2.125
Part A: Choose one value for a and one value for b that would make both of the following inequalities true:
a < b and |b| < |a|
Answers
The correct answer is, by choosing a = -2 and b = 1, we satisfy both inequalities .a < b:
To make both inequalities true, we need to select values for a and b that satisfy the given conditions:
a < b: This inequality means that the value of a should be less than the value of b.
|b| < |a|: This inequality means that the absolute value of b should be less than the absolute value of a.
One possible solution that satisfies both conditions is:
a = -2
b = 1
With these values, we have:
-2 < 1 (a < b)
|-1| < |2| (|b| < |a|)
Therefore, by choosing a = -2 and b = 1, we satisfy both inequalities.a < b:
This inequality states that the value of a should be less than the value of b. In other words, a needs to be positioned to the left of b on the number line. To satisfy this condition, we can choose a to be any number that is less than b. In the example I provided, a = -2 and b = 1, we can see that -2 is indeed less than 1, fulfilling the requirement.
|b| < |a|:
This inequality involves the absolute values of a and b. The absolute value of a number is its distance from zero on the number line, always resulting in a non-negative value. The inequality states that the absolute value of b should be less than the absolute value of a. To satisfy this condition, we can choose b to be any number with a smaller absolute value than a. In the example I provided, |1| is less than |(-2)|, as 1 is closer to zero than -2, fulfilling the requirement.
By selecting a = -2 and b = 1, we satisfy both inequalities: a < b and |b| < |a|. The specific values of -2 and 1 were chosen as an example, but there are multiple other values that would also satisfy the given conditions. The important aspect is that a is indeed less than b, and the absolute value of b is smaller than the absolute value of a.
Learn more about inequality here:
https://brainly.com/question/30238989
#SPJ8
What is the number that is divisible by 7?
13, 17, 91, or 771
Answers
Step-by-step explanation:
13÷7=1.85717÷7=2.42891÷7=13771÷7=110.142Hence,
91 is divisible by 7.
which describes the correct order of steps for constructing an angle bisector of ABC using only a straightedge and compass
Answers
Constructing an angle bisector using only a straightedge and compass involves drawing the Angle, creating two arcs that intersect the angle, and using those arcs to create a line segment that bisects the angle.
To construct an angle bisector using a straightedge and compass, there are several steps that you need to follow. The correct order of steps for constructing an angle bisector of ABC using only a straightedge and compass are listed below:
Step 1: Draw the angle ABC with a straightedge.
Step 2: Place the point of the compass on point B and swing an arc that intersects both lines that make up the angle. Label the two points where the arc intersects the angle as points D and E.
Step 3: Without changing the compass width, place the point of the compass on point D and swing an arc that intersects the ray that extends from point B. Label the point of intersection as point F.
Step 4: Without changing the compass width, place the point of the compass on point E and swing an arc that intersects the ray that extends from point B. Label the point of intersection as point G.
Step 5: Draw the line segment FG with a straightedge. This line segment is the angle bisector of angle ABC.
In summary, constructing an angle bisector using only a straightedge and compass involves drawing the angle, creating two arcs that intersect the angle, and using those arcs to create a line segment that bisects the angle. Following these steps will allow you to construct the angle bisector of ABC accurately.
For more questions on Angle.
https://brainly.com/question/31615777
#SPJ8