what does the unit of measurement known as a pascal measure?
Answers
Step-by-step explanation:
Pascal is a unit of pressure (or stress) it is a N/m^2
Related Questions
1. Given a random measurement process (X) with a population mean μ of 12 and population standard deviation σ of 1.5, perform the following calculations while assuming that the underlying random process is Gaussian: a. Give the probability that the next measurement x
i
is between 8 and 10 (i.e., P(8
i
is greater than 13 (i.e., P(X>12) ) c. What is the precision error of this measurement process?
Answers
First, we need to standardize the values using the population mean and standard deviation:
Z1 = (8 - μ) / σ
Z2 = (10 - μ) / σ
Substituting the values:
Z1 = (8 - 12) / 1.5 = -2.67
Z2 = (10 - 12) / 1.5 = -1.33
Now, we can use a standard normal distribution table or a calculator to find the cumulative probabilities corresponding to these z-values. The probability that the next measurement xi is between 8 and 10 is given by:
P(8 < xi < 10) = P(Z1 < Z < Z2)
Using the standard normal distribution table or calculator, we find the corresponding probabilities and subtract to get the desired result.
b. To calculate the probability that the next measurement xi is greater than 13, we can follow a similar approach.
Z = (13 - μ) / σ
Z = (13 - 12) / 1.5 = 0.67
P(X > 12) = P(Z > 0.67)
Using the standard normal distribution table or calculator, we can find the probability corresponding to the given z-value.
c. The precision error of the measurement process can be represented by the standard deviation of the population (σ). In this case, the precision error is given as 1.5, which is the population standard deviation. It represents the average amount of variation or spread in the measurements from the population mean.
Describe a strategy for determining the input when you know the percent change and output.Use this example if it helps you to explain your thinking

Answers
Let I represent the Input and O, the output.
The strategy for determining the imput, I, is to mulitplying the Output, O by 100 and then dividing the result by the difference between 100 and the given percentage.
Mathematically, the input , I, is:
\(I=\frac{100O}{100-P}\)3. What is the volume of the composite figure? (Use 3.14 as a approximate value of TT
and round final answer to the nearest whole number)

Answers
Answer :
4055
explanation :
v= n r² h/3 = n × 11² × 32/2 = 4054.74 round up to 4055
8 3/4 + 9 5/9=
with working?
Answers
8 3/4 + 9 5/9 Add 8 and 9
17 + 3*9/4*9 + 5*4/9*4 Find common denominator
17 + 27/36 + 20/36 Add
17 + 47/36 Convert into mixed fraction
17 + 1 11/36 Simplify mixed fraction
18 11/36. Answer
If you need the decimal form, it is 18.31. But other than that, the answer is 18 11/36.
Simplify the expression and write the result in standard form, a+bi. Write all numbers as integers or simplified fractions.
-14 + √-125 / 10
Answers
Answer:
\( - 14 + \sqrt{ \frac{ - 5 \times 5 \times 5}{10} } \)
\( - 14 + 5 \sqrt{ \frac{ - 1}{2} } \)
\( - 14 + \frac{5 \sqrt{ - 1} }{ \sqrt{2} } \)
\( - 14 + \frac{5i}{ \sqrt{2} } \)
Step-by-step explanation:
\( - 14 + \sqrt{ \frac{ - 125}{10} } \\ - 14 + \frac{5 \sqrt{5} i}{ \sqrt{10} } \\ = - 14 + \frac{5i}{ \sqrt{2} } \\ = - 14 + \frac{5i \sqrt{2} }{ \sqrt{2} \times \sqrt{2} } \\ - 12 + \frac{5 \sqrt{2}i }{2} \\ thank \: you\)
Select the correct answer. What is the vertex of the parabola given by y = -(x − 2)^2 − 1?
Answers
Answer:
vertex: -2,1
Step-by-step explanation:
You need to graph it.
Convert 1.19rads to degree
Answers
Answer:
68.2 degrees
Step-by-step explanation:
\(1.19\frac{180}{\pi }\)
\(68.2\) degrees
In a class of 25 students, 5 have a brother and 11 have a sister. There are 2
students who have a brother and a sister. What is the probability that a
a
student chosen randomly from the class has a brother and a sister?
а
Answers
Answer:
2/25
Step-by-step explanation:
Find the inverse Laplace transform of (4+9s)/s^2
The inverse Laplace transform of of (4+9s)/s^2 is
Answers
The inverse Laplace transform of (4+9s)/s^2 is given by f(t) = 4t + 9, where f(t) represents the time-domain function.
To find the inverse Laplace transf
orm of (4+9s)/s^2, we can use the property that the inverse Laplace transform of a constant multiplied by a term of the form s^n is equal to t^(n-1)/((n-1)!).
In this case, we have (4+9s)/s^2, which can be rewritten as 4/s^2 + 9s/s^2. Applying the property mentioned above, we get the inverse Laplace transform of 4/s^2 as f₁(t) = 4t and the inverse Laplace transform of 9s/s^2 as f₂(t) = 9.
Therefore, the inverse Laplace transform of (4+9s)/s^2 is the sum of f₁(t) and f₂(t), which gives us f(t) = 4t + 9. Thus, the time-domain function is f(t) = 4t + 9.
Learn more about function : brainly.com/question/31062578
#SPJ11
The difference of the same side interior angles of two parrelels lines is 50 degrees find all angles
Answers
Answer:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
Step-by-step explanation:
Angle 1: Same-side interior angle of Line 1
Angle 2: Same-side interior angle of Line 2
We know that the difference between the angles is 50 degrees. Since the angles are supplementary, we can write the equation:
Angle 1 + Angle 2 = 180
Now, we need to express the difference between the angles in terms of Angle 1 or Angle 2. We can choose either angle, so let's express it in terms of Angle 1:
Angle 1 - Angle 2 = 50
We can rewrite this equation as:
Angle 1 = 50 + Angle 2
Now substitute this expression for Angle 1 into the first equation:
(50 + Angle 2) + Angle 2 = 180
Combine like terms:
2Angle 2 + 50 = 180
Subtract 50 from both sides:
2Angle 2 = 130
Divide by 2:
Angle 2 = 65
Now substitute this value back into the equation for Angle 1:
Angle 1 = 50 + Angle 2
Angle 1 = 50 + 65
Angle 1 = 115
Therefore, the angles are as follows:
Angle 1 = 115 degrees
Angle 2 = 65 degrees
Given the functions
f(x)=125 + 15x and g(x)=12x+140, find the value of x for which f(x)=g(x).
X=
Please hurry :)
Answers
Answer:
X = 5
Step-by-step explanation:
So what the equation is saying is that f(x) = g(x) so these equations are equal
The equation will look like this
125 + 15x = 12x + 140
I first began with subtracting the 12x from the 15x which will give you 3x
125 + 3x = 140
now we subtract 125 to 140 and you'll get 15
140-125 = 15 now divide by 3 leaving the x solo
15/3 = 5 so x is 5
hope that helps
Please help
...................

Answers
Answer:
It is the third one!
Step-by-step explanation:
Find x in the triangle
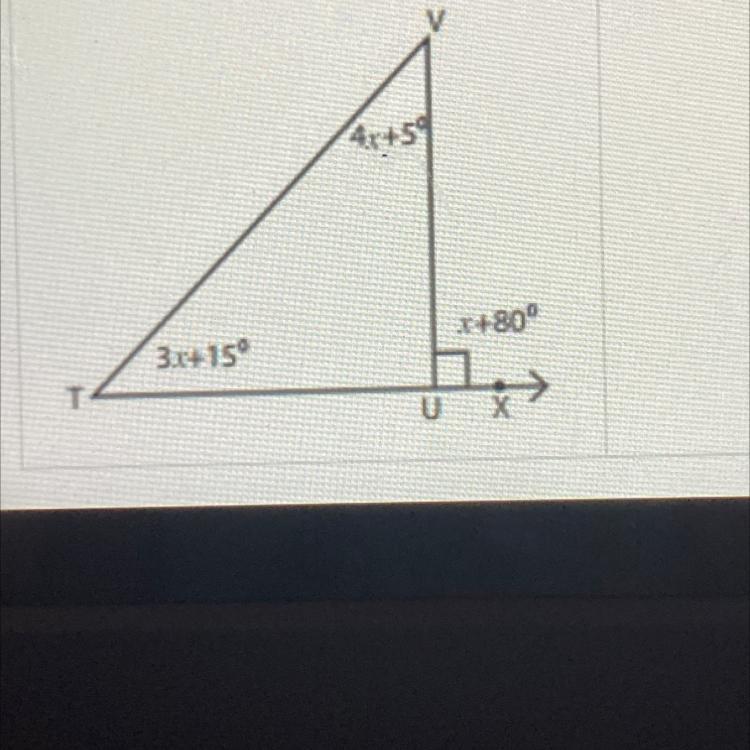
Answers
Answer:
15
Step-by-step explanation:
which expression is a possible leading term for the polynomial function graphed below? –18x14 –10x7 17x12 22x9
Answers
Among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
The leading term of a polynomial function is the term containing the highest power of the variable. Among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
The degree of a polynomial function is the highest degree of any of its terms.
If a polynomial has only one term, then the degree of that term is the degree of the polynomial and is also called a monomial.
For example, consider the given function:Now, observe the degree of the function, which is 14, as the highest exponent of the function is 14.
Thus, the term containing the highest power of the variable x is -18x¹⁴.
Therefore, among the given expressions, the one that could be the possible leading term for the polynomial function graphed below is -18x¹⁴.
To know more about probability visit :-
https://brainly.com/question/1496352
#SPJ11
8+y−23k+3m What is the constant? What is the coefficient of the y term? How many terms are there?
Answers
Answer:
Step-by-step explanation:
There are 4 terms
Coefficient of y term = 1
Constant = 8
The term without variable is the constant term.
Which statement is true regarding the functions on the
graph?
A. f(-3) = g(-4)
B. f(-4) = g(-3)
C. f(-3) = g(-3)
D. f(-4) = g(-4)

Answers
Answer:
C. f(-3) = g(-3)
Step-by-step explanation:
Let's look at each option to which one is true with regard to the given functions on the graph.
The option that is correct is the option that shows where the graph of f(x) and g(x) intercepts or cut across each other.
Now, take a look at the graph, the line of both functions intercepts at x = -3. At this point, the value of f(-3) and g(-3) is equal to -4.
Therefore: f(-3) = g(-3)
I need Help can someone please help me with this. Write an equation of a function with each domain: A. [2, [infinity]) B. (-[infinity], [infinity]) C. (2, [infinity])
Answers
Step-by-step explanation:
A.
\(f(x) = \sqrt{x - 2} \)
B.
\(g(x) = 2x \)
C.
\(h(x) = \frac{1}{x - 2 \: } \: \: \: \: h(x) = x where x is greater than zero
help!
50 pts and brainiest

Answers
Answer:
303
Step-by-step explanation:
add all of them and you get 303, hope this helps :)
Answer:
Vertical. A vertical is an alignment in which the top is always above the bottom. It is a property of two or more points in which if a point is directly below the ...
Step-by-step explanation:
sketch the graph of the probability density function over the indicated interval. f(x) = 1 10 , [0, 10]
Answers
The graph of the probability density function f(x) = 1/10 over the interval [0, 10] is a flat, horizontal line at y = 1/10.
The probability density function (PDF) f(x) = 1/10, defined over the interval [0, 10], represents a uniform distribution. In a uniform distribution, the probability of any value within the interval is constant, indicating that all values are equally likely to occur.
To sketch the graph of this PDF, we can plot the function f(x) = 1/10 on a coordinate plane.
First, we set up the axes. We label the x-axis to represent the interval [0, 10], where 0 is the lower limit and 10 is the upper limit. The y-axis represents the probability density.
Next, we plot the points on the graph. Since the PDF is a constant function, the value of f(x) = 1/10 for all x in the interval [0, 10]. Therefore, we mark a horizontal line at y = 1/10 across the entire interval.
The horizontal line represents a flat line parallel to the x-axis. The height of the line is 1/10, indicating that the probability density is constant throughout the interval [0, 10]. This means that any value within the interval has an equal probability of occurring.
The graph visually represents the uniform distribution, where the probability is evenly distributed across the entire interval.
Learn more about probability density function at: brainly.com/question/31039386
#SPJ11
what is 0.08 written as a percant
Answers
It is 8%
Hope I helped
Answer:
8%=0.08 because 0.08 is 8/100 and 8% is also 8/100
Step-by-step explanation:
how many solutions does the graph above show?
a. one
b. none
c. infinite

Answers
Answer:
infinite
Step-by-step explanation:
The line can be represented by the equation y=-2/3x-2 since there are no other lines it would be infinite. if there was a line with the same slope and a different y-intercept the answer would be none as the lines never intersect. for the equation there are ifinitly many!
for example any point that that lone touches is a solutions so there is not one but many answers.
The solution candidates y1(t)=Aeαtcos(βt) and y2(t)=Beαtsin(βt) when the characteristic equation has complex roots r1,2=α±βir1, are based on pure luck and have no 'deeper' explanation, except for plugging them into the equation and showing that they work.
a. true b. false
Answers
The coefficients A and B are determined by the initial conditions of the differential equation. Therefore, the solutions are not based on luck, but on a rigorous mathematical derivation. The given statement is false.
The solution candidates y1(t)=A\(e^{(\alpha t)\)cos(βt) and y2(t)=B\(e^{(\alpha t)\)sin(βt) for a second-order linear differential equation with constant coefficients and complex roots r1,2=α±βi are not based on pure luck. They are derived using the fact that complex exponential functions can be written as a linear combination of real exponential functions and trigonometric functions through Euler's formula:
e^(α+βi)t = e^αt(cos(βt) + i sin(βt))
Taking the real and imaginary parts of this equation, we get:
e^(αt)cos(βt) = Re(e^(α+βi)t) and e^(αt)sin(βt) = Im(e^(α+βi)t)
So, the solutions y1(t) and y2(t) can be written as linear combinations of exponential functions and trigonometric functions. The coefficients A and B are determined by the initial conditions of the differential equation. Therefore, the solutions are not based on luck, but on a rigorous mathematical derivation.
To learn more about trigonometric functions visit: https://brainly.com/question/6904750
#SPJ11
can you tell me if my answer is correct
Answers
Answer:
(a)Vertex
(c)3 seconds
Explanation:
Part A
The maximum point on a parabola is called the Vertex.
Part C
To find out how much the plain was in the air, find the values of t at which the height, h=0.
Next, subtract the second value of t from the first value.
\(h=-16t^2+32t+48\)First, set h=0:
\(\begin{gathered} h=-16t^2+32t+48=0 \\ -16t^2+32t+48=0 \end{gathered}\)Factorize:
\(\begin{gathered} -16(t^2-2t-3)=0 \\ t^2-2t-3=0 \\ t^2-3t+t-3=0 \\ t(t-3)+1(t-3)=0 \\ (t+1)(t-3)=0 \\ t+1=0\text{ or }t-3=0 \\ t=-1\text{ or }t=3 \end{gathered}\)Therefore, the plane hits the ground after 3 seconds.
In evaluating the results for your area, which of the following trends emerges from the data?
a. Increased Overtime Hours lead to increased Productivity Rates
b. Productivity Rate is negatively impacted by team size
c. Schedule Adherence is inconsistent across periods of time
d. Larger teams have more Schedule Adherence issues
Answers
To evaluate the results for your area and identify the emerging trends from the data, we need to examine the relationships between different variables. Based on the options provided:
a. Increased Overtime Hours lead to increased Productivity Rates: This trend suggests that as the number of overtime hours increases, productivity rates also increase. However, without specific data and analysis, it is difficult to confirm this trend.
b. Productivity Rate is negatively impacted by team size: This trend indicates that larger team sizes result in lower productivity rates. This suggests that as the team size increases, individual performance and coordination may be compromised, leading to decreased productivity.
c. Schedule Adherence is inconsistent across periods of time: This trend suggests that adherence to schedules fluctuates over time. It indicates that there is variability in meeting scheduled timelines or deadlines, potentially due to factors such as workload, resource availability, or changing priorities.
d. Larger teams have more Schedule Adherence issues: This trend implies that larger teams face challenges in adhering to schedules. It suggests that coordination and communication within larger teams may be more complex, leading to difficulties in meeting scheduled timelines or maintaining adherence.
It is important to note that without specific data and statistical analysis, it is challenging to determine the accurate trend from the given options. Proper data analysis and interpretation would be required to draw definitive conclusions about the relationships between variables in your specific area.
To learn more about data click here:brainly.com/question/29117029
#SPJ11
Let X1, X2, ..., X100 be independent discrete random variables, each with probability mass function (pmf) p(x) = 1 x for x = 1, 2, 3,4. a. Use the central limit theorem to approximate P(3< Xi+X2+...+X 100 <3.2). 100 b. Use R to simulate the problem and estimate the probability in part (a). Then compare your answers to parts (a) and (b).
Answers
Comparing the results from parts (a) and (b) will allow us to assess the accuracy of the approximation made using the central limit theorem.
(a) To approximate the probability P(3 < Xi+X2+...+X100 < 3.2) using the central limit theorem, we can consider the sum of the random variables Xi+X2+...+X100 as a sample mean. Since the random variables Xi are independent and identically distributed, the sum follows a normal distribution as n (the number of variables) increases. We can calculate the mean and variance of the individual random variables, which are 2.5 and 1.25, respectively. Then, we can approximate the probability using the standard normal distribution by standardizing the values (subtracting the mean and dividing by the standard deviation).
(b) Using R, we can simulate the problem by generating a large number of random samples from the given distribution and calculating the proportion of samples that satisfy the condition 3 < Xi+X2+...+X100 < 3.2. By repeating this simulation multiple times, we can estimate the probability.
Learn more about central limit theorem here: brainly.com/question/898534
#SPJ11
how to calculate the porbablitiy of something happening between two indepednent normallhy distributed things given mean and standard deviation
Answers
A standard normal distribution table, or a calculator with a built-in CDF function for the standard normal distribution to calculate this probability.
To calculate the probability of an event occurring between two independent normally distributed variables, we can use the standard normal distribution and the properties of linear combinations of normal variables.
Suppose we have two independent random variables X and Y that are normally distributed with means μX and μY, and standard deviations σX and σY, respectively. Let Z be a linear combination of X and Y given by Z = aX + bY, where a and b are constants.
Then, Z is also normally distributed with mean μZ = aμX + bμY and standard deviation σZ = sqrt(a^2 * σX^2 + b^2 * σY^2).
To calculate the probability of an event occurring between two values, say a and b, for the variable Z, we first standardize Z to a standard normal variable Z* using the formula:
Z* = (Z - μZ) / σZ
Then, we can use the cumulative distribution function (CDF) of the standard normal distribution to calculate the probability of the event occurring between a and b as:
P(a < Z < b) = P[(a - μZ) / σZ < Z* < (b - μZ) / σZ]
We can use statistical software, a standard normal distribution table, or a calculator with a built-in CDF function for the standard normal distribution to calculate this probability.
Learn more about probability here
https://brainly.com/question/13604758
#SPJ11
Angle 1 = 3x - 4
Angle 3 = 5x - 38
Find the measure of Angle 4
Answers
The measure of angle 4 is 133° and is equal to Angle 2 because there are corresponding angles formed by parallel lines cut by a transversal.
What are corresponding anglesCorresponding angles are the angles that are formed when two parallel lines are cut or intersected by the transversal and they are equal.
The angles 1, 2, 3 and 4 all lie on a transversal line that cuts the parallel lines, hence angles 1 and 3 are corresponding angles are they are equal, also angles 2 and 4 are corresponding angles and they are equal.
so;
5x - 38 = 3x - 4 {collect like terms}
5x - 3x = 38 - 4
2x = 34 {divide through by 2}
x = 17
angle 3 = 5(17) - 38
angle 3 = 85 - 38
angle 3 = 47°
angle 4 = 180° - 47° {angles 3 and 4 are supplementary angles so their sum is equal to 180°}
angle 4 = 133°
Therefore, the measure of the angle 4 is equal to 133° since it is a supplementary angle to angle 3 and it corresponds to the angle 2.
Know more about corresponding angles here:https://brainly.com/question/2009183
#SPJ1

what does the greek letter delta that is represented by a ∆ mean?

Answers
Answer:
“change” or “the change”
Step-by-step explanation:
What formula should be entered to calculate the total budget?
Answers
Answer:
The tatal budget of what, there's no budget the budget down so I can do the problem.
I don’t even know what I just typed please help me!!!
Which means "four thirds of the product of pi and the cube of the radius"?
A. 4/3pi r3
B. 4pi r
C. 4/3 + 3 < pi r
D. 4/3 + 3 pi r3
I don’t need an explanation btw:)
Answers
Answer:
Option A
Step-by-step explanation:
=> \(\frac{4}{3} \pi r^3\)