What do static electricity and current electricity have in common.
Answers
Answer: Static electricity is uncontrolled electrons passing from one body to another in sudden, momentary movements, while current electricity is when the electrons are controlled by moving along a path together.
HAVE A BLESSED DAY!!!!
Related Questions
PLEASE HELP!! IT'S IN THE PIC, PYTHAGOREAN THEOREM: a² + b² = c²
Thanks in advance

Answers
What is the value of 532x13
Answers
Answer:
the value of 532×13=6,916
Nolan is going to a carnival that has games and rides. Each game costs $2.50
and each ride costs $3.50. Nolan spent $52.50 altogether on 17 games and
rides. Write a system of equations that could be used to determine the
number of games Nolan played and the number of rides Nolan went on.
Define the variables that you use to write the system.
Answers
Hence, the equation is of the form \(2.5x+3.5y=52.50\).
What is the system of equation?
A system of equations, also known as a set of simultaneous or an equation system, is a finite set of equations for which we sought the common solutions.
Here given that,
Nolan is going to a carnival that has games and rides. Each game costs $\(2.50\) and each ride costs $\(3.50\). Nolan spent $\(52.50\) altogether on \(17\) games and rides.
So, let us assume that the number of games are \(x\) and the number of rides are \(y\).
So, the equation is of the form
\(2.5x+3.5y=52.50 ........(1)\)
And Noaln spent altogether $\(52.50\) on \(17\) games and rides.
So,
\(x+y=17\)
Then,
\(2.5x+2.5y=2.5(x+y)\\As,\\x+y=17\\So,\\=2.5(17)\\\\=42.5.....(2)\)
Now, subtract equation \((2)\) from equation \((1)\), we get
\(x=52.5-42.5\\\\x=10\)
\(y=17-10\\y=7\)
So the equation is of the form
\(2.5(7)+3.5(10)=52.50\\17.5+35=52.50\\52.50=52.50\)
Hence, the equation is of the form \(2.5x+3.5y=52.50\).
To know more about the system of equation
https://brainly.com/question/76528
#SPJ1
Question 1
The double box-and-whisker plot shows the goals scored per game by two hockey teams during a 20-game season.
Answers
Based on the information in the graph, it can be inferred that team B scores 4 more goals per game.
How do you compare populations using measures of center and median?To compare the populations using measures of center and median we must carry out the following procedure:
Team A
Median = 3
Q₁ = 2
Q₃ = 4
IQR = Q₃ - Q₁ = 4 - 2 = 2
Team B
Median = 7
Q₁ = 6
Q₃ = 8
IQR = Q₃ - Q₁ = 8 - 6 = 2
According to the information above, the variation in goals scored is the same. However, team B usually scores 4 more goals than team A for each game.
Additionally, the difference in the mean of these two values is 2.
Note: This question is incomplete. Here is the complete information:
Attached image
Learn more about hockey in: https://brainly.com/question/30064061
#SPJ1

A long, straight wire lies along the y-axis and carries current in the positive y-direction. A positive point charge moves along the x-axis in the positive x-direction. The magnetic force that the wire exerts on the point charge is in
Answers
The magnetic force that the wire exerts on the point charge is in the negative z-direction.
When a current-carrying wire and a moving point charge are placed in a magnetic field, a magnetic force is exerted on the moving charge due to the interaction between the magnetic field and the charge's velocity. According to the right-hand rule, the direction of the magnetic force is perpendicular to both the velocity of the moving charge and the magnetic field created by the current-carrying wire.
In this scenario, the wire carrying current in the positive y-direction generates a magnetic field that circulates around the wire. The point charge moving along the x-axis in the positive x-direction experiences a magnetic force directed perpendicularly to both the velocity (positive x-direction) and the magnetic field (circulating around the wire). Applying the right-hand rule, the magnetic force is found to be in the negative z-direction, which is downward and perpendicular to the x and y axes.
Learn more about magnetic force here:
https://brainly.com/question/30532541
#SPJ11
A rectangle is 7 feet long by 2 feet wi
lf 2 feet are added to the length of the
would be the area, in square feet
Answers
Answer:
Step-by-step explanation:
L = W+2A = 63 = W × (W+2)W^2 + 2W = 63W^2 + 2W — 63 =0(W+9)(W-7) = 0W = 7….. L = W+2 = 9Dimenions are 9′ × 7′
True/False based on the t-test assuming equal variances on the t-testequal worksheet, it is reasonable to assume that the variances are equal?
Answers
Based on the t-test assuming equal variances a. Examining the ratio of the variances, it is reasonable to conclude that the variances are unequal."
It is vital to establish whether or not the variances of the two groups being compared are indeed identical before performing a t-test under the assumption of equal variances. This is significant since the t-calculation statistic depends on the assumption that variances are equal.
One can look at the ratio of the variances between the two groups to evaluate the assumption of equal variances. Typically, it is acceptable to infer that the variances are not equal if the ratio of the variances is more than two or lower than half. One can presume that the variances are equal in the absence of such proof. Since the variances are not equal, it is not logical to infer that they are.
Complete and correct Question:
Based on the t-test assuming equal variances on the T-Test Equal worksheet, is it reasonable to assume that the variances are equal?
a. Examining the ratio of the variances, it is reasonable to conclude that the variances are unequal.
b. Whether the variances are equal or not is not relevant for this situation.
c. Examining the ratio of the variances, it is reasonable to conclude that the variances are equal.
d. It is impossible to determine if the variances are equal given the data we have.
Read more about T-tests on:
https://brainly.com/question/6501190
#SPJ4
A rectangular cotton field is 525 feet wide. The field of cotton has a perimeter of 2025 feet. Which equation represents the cotton field
Answers
Answer:
hi
Step-by-step explanation:
A bus has three passengers Crew Marty Blakely. Marty's age is 1.5 times Crew's age. Blakely's age is 0.75 times crew's age. If the sum of the tree passengers is 104,find the age of each passenger
Answers
The ages of the crew, Marty and Blakeley are 32 years, 48 years and 24 years respectively.
AlgebraCrew's age = xMarty's age = 1.5xBlakely's age = 0.75xTotal ages = 104Total = crew's age + Marty's age + blakely's age
104 = x + 1.5x + 0.75x
104 = 3.25x
x = 104 ÷ 3.25
x = 32 years
Therefore,
Crew's age = x
= 32 years
Marty's age = 1.5x
= 1.5(32)
= 48 years
Blakely's age = 0.75x
= 0.75(32)
= 24 years
Learn more about algebra:
https://brainly.com/question/4344214
#SPJ1
Assume that the height, X, of a college woman is a normally distributed random variable with a mean of 65 inches and a standard deviation of 3 inches. Suppose that we sample the heights of 180 randomly chosen college women. Let M be the sample mean of the 180 height measurements. Let S be the sum of the 180 height measurements. All measurements are in inches. a) What is the probability that X < 59? b) What is the probability that X > 59? c) What is the probability that all of the 180 measurements are greater than 59? d) What is the expected value of S? e) What is the standard deviation of S? f) What is the probability that S-180*65 >10? g) What is the standard deviation of S-180*65 h) What is the expected value of M? i) What is the standard deviation of M? j) What is the probability that M >65.41? k) What is the standard deviation of 180*M? l) If the probability of X > k is equal to .3, then what is k?
Answers
a) The probability that X < 59 is approximately 0.0013.
b) The probability that X > 59 is approximately 0.9987.
c) The probability that all of the 180 measurements are greater than 59 is approximately 0.9987^180.
d) The expected value of S is 180 * 65 = 11700 inches.
e) The standard deviation of S is 180 * 3 = 540 inches.
f) The probability that S - 180 * 65 > 10 is approximately 0.9997.
g) The standard deviation of S - 180 * 65 is 540 inches.
h) The expected value of M is 65 inches.
i) The standard deviation of M is 3 / √180 inches.
j) The probability that M > 65.41 is approximately 0.3476.
k) The standard deviation of 180 * M is 3 inches.
l) If the probability of X > k is equal to 0.3, then k is approximately 67.39 inches.
To find the probability that X < 59, we need to calculate the z-score first. The z-score formula is (X - μ) / σ, where X is the value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get a z-score of (59 - 65) / 3 = -2. Therefore, using the z-table or a calculator, we find that the probability is approximately 0.0013.
Similarly, to find the probability that X > 59, we can use the z-score formula. The z-score is (59 - 65) / 3 = -2. The probability of X being greater than 59 is equal to 1 minus the probability of X being less than or equal to 59. Using the z-table or a calculator, we find that the probability is approximately 0.9987.
The probability that all of the 180 measurements are greater than 59 is the probability of one measurement being greater than 59 raised to the power of 180. Since the probability of a single measurement being greater than 59 is approximately 0.9987, the probability of all 180 measurements being greater than 59 is approximately \(0.9987^1^8^0\).
The expected value of S is the sum of the expected values of the individual measurements. Since the mean height is 65 inches, the expected value of each measurement is 65. Since we have 180 measurements, the expected value of S is 180 * 65 = 11700 inches.
The standard deviation of S is the square root of the sum of the variances of the individual measurements. Since the standard deviation of each measurement is 3 inches, the variance is 3² = 9. Since we have 180 measurements, the variance of S is 180 * 9 = 1620 inches². Taking the square root, we get the standard deviation of S as √1620 = 540 inches.
To find the probability that S - 180 * 65 > 10, we need to calculate the z-score for the difference. The z-score formula is (X - μ) / σ, where X is the value, μ is the mean, and σ is the standard deviation. Plugging in the values, we get a z-score of (10 - 0) / 540 = 0.0185. Using the z-table or a calculator, we find that the probability is approximately 0.9997.
The standard deviation of S - 180 * 65 is the same as the standard deviation of S, which is 540 inches.
The expected value of M, the sample mean, is equal to the population mean, which is 65 inches.
The standard deviation of M, denoted as σ_M, is given by σ / √n, where σ is the standard deviation of the population and n is the sample size. Plugging in the values, we get σ_M = 3 / √180 inches.
To find the probability that M > 65.41, we need to calculate the z-score for M. The z-score formula is (X - μ) / (σ / √n), where X is the value, μ is the mean, σ is the standard deviation of the population, and n is the sample size. Plugging in the values, we get a z-score of (65.41 - 65) / (3 / √180) ≈ 0.733. Using the z-table or a calculator, we find that the probability is approximately 0.3476.
The standard deviation of 180 * M is equal to the standard deviation of M divided by the square root of 180. Since the standard deviation of M is 3 / √180 inches, the standard deviation of 180 * M is 3 inches.
If the probability of X > k is equal to 0.3, we need to find the corresponding z-score from the z-table or using a calculator. The z-score represents the number of standard deviations away from the mean. From the z-score, we can calculate the value of k by rearranging the z-score formula: z = (k - μ) / σ. Solving for k, we get k = z * σ + μ. Plugging in the values, we get k = 0.5244 * 3 + 65 ≈ 67.39 inches.
Learn more about Probability
brainly.com/question/30881224
#SPJ11
2x-y=-2 3x-3y=15 método gráfico
Answers
Answer:
Cómo se vería si estuviera graficado:
2x−y=−2
3x−3y=15
Cómo se vería si lo resolviera graficando:
(−7,−12)
Answer:
Step-by-step explanation:
2x - y = -2
3x - 3y = 15
-6x + 3y = 6
3x - 3y = 15
-3x = 21
x = -7
2(-7) - y = -2
-14 - y = -2
-y = 12
y = -12
(-7, -12)
10. A line passes through points (4, 18) and (6x,2k). What is the slope of the line?
8k-9
12x-4
A
B
2k-9
6x-4
C
D
k-9
3x-2
2k-9
3x-4

Answers
The slope of the line which passes through the points (4, 18) and (6x, 2k) is (k - 9)/(3x - 2).
According to the given question.
A line passes through points (4, 18) and (6x,2k).
Which means we have two points (4, 18) and (6x,2k).
As we know that, the slope of a line is the ratio of the amount that y increases as x increases some amount.And the slope formula is m=(y2-y1)/(x2-x1) if a lines passes through the point (x2, y2) and (x1, y1).
Therefore, the slope of the line which passes through the points (4, 18) and (6x,2k)
= 2k - 18/ 6x - 4
= 2[k - 9]/2[3x - 2]
= (k-9)/(3x - 2)
Hence, the slope of the line which passes through the points (4, 18) and (6x, 2k) is (k - 9)/(3x - 2).
Find out more inofrmation about slope of line here:
https://brainly.com/question/14511992
#SPJ1
Solve for x and graph the solution on the number line below.

Answers
Answer:
\(-6\leq x < 5\)
Step-by-step explanation:
Given compound inequality:
\(31 \geq-4x+7\;\;\;\textsf{and}\;\;\;-4x+7 > -13\)
Solve the first inequality:
\(\begin{aligned}31 & \geq -4x+7\\\\31 +4x& \geq -4x+7+4x\\\\4x+31& \geq 7\\\\4x+31-31 & \geq 7-31\\\\4x & \geq -24\\\\\dfrac{4x}{4} & \geq \dfrac{-24}{4}\\\\x & \geq -6\end{aligned}\)
Solve the second inequality:
\(\begin{aligned}-4x+7& > -13\\\\-4x+7-7& > -13-7\\\\-4x& > -20\\\\\dfrac{-4x}{-4}& > \dfrac{-20}{-4}\\\\x& < 5\end{aligned}\)
Therefore, combining the solutions, the solution to the compound inequality is:
\(\large\boxed{-6\leq x < 5}\)
When graphing inequalities:
< or > : open circle.≤ or ≥ : closed circle.< or ≤ : shade to the left of the circle.> or ≥ : shade to the right of the circle.To graph the solution:
Place a closed circle at x = -6.Place an open circle at x = 5.Connect the circles with a line.
10 pack of 2.3 ounce bars at $17.35
Answers
10pack------------>$17.35
1 pack-------------->x
using cross multiplication
10/1 = 17.35/x
Solving for x:
x = 17.35/10 = $1.735
Therefore each pack costs $1.735
10+\frac{3}{4}y=
10+
4
3
y=
\,\,43
43
Answers
Um, is there a possibility that you could clean this question up a bit? It is a little scrambled and hard to make out of the equation given. Thanks!
If three farmers share some bags of fertilizers in the ratio 3:4:5.if the smallest share is 18 bags.what is the largest share
Answers
Answer:
30
Step-by-step explanation:
Sum of the ratios = 3 + 4 + 5 = 12
Smallest share = 18 bags
Ratio of the smallest share = 3
Let the largest share = x
From the question
18 ------------ 3
x --------------5
Cross multiply
3x = 18 × 5
Dividing bothsides by 3
X = 18 × 5/ 3
X = 90 / 3
X = 30
Therefore.
The largest share = 30
14÷966 I need help doing this pls help
Answers
Answer:
0.01
Step-by-step explanation:
i hope this help only that u need to do next time is to divide 966 with a number that is close to the sum
A shipment of 14 television sets includes three that are defective. In how many wats can a hotel purchase four of these sets and receive at least two of the defective sets?
Answers
The hotel can purchase four television sets from the shipment in 36 different ways and can receive at least two defective sets.the hotel can purchase four television sets from the shipment in 177 different ways and receive at least two of the defective sets.
Step 1: Calculate the number of ways to choose 4 television sets from the shipment of 14. This can be done using the combination formula: C(n, k) = n! / (k! * (n-k)!), where n is the total number of items and k is the number of items to be chosen. In this case, n = 14 and k = 4.
C(14, 4) = 14! / (4! * (14-4)!) = 14! / (4! * 10!) = (14 * 13 * 12 * 11) / (4 * 3 * 2 * 1) = 1001.
Step 2: Calculate the number of ways to choose at least 2 defective sets from the 3 defective sets available. This can be done by considering the possible combinations: choosing 2 defective and 2 non-defective, choosing 3 defective and 1 non-defective, or choosing all 3 defective sets.
Number of ways to choose 2 defective and 2 non-defective: C(3, 2) * C(11, 2) = 3 * 55 = 165.
Number of ways to choose 3 defective and 1 non-defective: C(3, 3) * C(11, 1) = 1 * 11 = 11.
Number of ways to choose all 3 defective sets: C(3, 3) * C(11, 0) = 1 * 1 = 1.
Step 3: Add up the results from Step 2 to get the total number of ways to choose at least 2 defective sets: 165 + 11 + 1 = 177.
Therefore, the hotel can purchase four television sets from the shipment in 177 different ways and receive at least two of the defective sets.
Learn more about combination : brainly.com/question/20211959
#SPJ11
Dan invests £6800 into his bank account. He receives 5% per year compound interest. How much will Dan have after six years? Give your answer to the nearest penny where appropriate
Answers
Answer:
£6800 times (1.05)to the power of 6
=£9112.65
Step-by-step explanation:
Find the power set for the following sets (Write 3 examples of each)
a) Two sets A & B both having any 2 elements
b) Two sets A & B both having any 3 elements
c) Two sets A & B both having any 4 elements
Answers
Given statement solution is :- a) Power set for two sets A and B with any 2 elements:
Set A: {1, 2}, Set B: {3, 4}
Power set of A: {{}, {1}, {2}, {1, 2}}
Power set of B: {{}, {3}, {4}, {3, 4}}
b) Power set for two sets A and B with any 3 elements:
Set A: {1, 2, 3}, Set B: {4, 5, 6}
Power set of A: {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Power set of B: {{}, {4}, {5}, {6}, {4, 5}, {4, 6}, {5, 6}, {4, 5, 6}}
c) Power set for two sets A and B with any 4 elements:
Set A: {1, 2, 3, 4}, Set B: {5, 6, 7, 8}
Power set of A: {{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}
Power set of B: {{}, {5}, {6}, {7}, {8}, {5, 6}, {5, 7}, {5, 8}, {6, 7}, {6, 8}, {7, 8}, {5, 6, 7}, {5, 6, 8}, {5, 7, 8}, {6, 7, 8},
a) Power set for two sets A and B with any 2 elements:
Set A: {1, 2}, Set B: {3, 4}
Power set of A: {{}, {1}, {2}, {1, 2}}
Power set of B: {{}, {3}, {4}, {3, 4}}
Set A: {apple, banana}, Set B: {cat, dog}
Power set of A: {{}, {apple}, {banana}, {apple, banana}}
Power set of B: {{}, {cat}, {dog}, {cat, dog}}
Set A: {red, blue}, Set B: {circle, square}
Power set of A: {{}, {red}, {blue}, {red, blue}}
Power set of B: {{}, {circle}, {square}, {circle, square}}
b) Power set for two sets A and B with any 3 elements:
Set A: {1, 2, 3}, Set B: {4, 5, 6}
Power set of A: {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Power set of B: {{}, {4}, {5}, {6}, {4, 5}, {4, 6}, {5, 6}, {4, 5, 6}}
Set A: {apple, banana, orange}, Set B: {cat, dog, elephant}
Power set of A: {{}, {apple}, {banana}, {orange}, {apple, banana}, {apple, orange}, {banana, orange}, {apple, banana, orange}}
Power set of B: {{}, {cat}, {dog}, {elephant}, {cat, dog}, {cat, elephant}, {dog, elephant}, {cat, dog, elephant}}
Set A: {red, blue, green}, Set B: {circle, square, triangle}
Power set of A: {{}, {red}, {blue}, {green}, {red, blue}, {red, green}, {blue, green}, {red, blue, green}}
Power set of B: {{}, {circle}, {square}, {triangle}, {circle, square}, {circle, triangle}, {square, triangle}, {circle, square, triangle}}
c) Power set for two sets A and B with any 4 elements:
Set A: {1, 2, 3, 4}, Set B: {5, 6, 7, 8}
Power set of A: {{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}
Power set of B: {{}, {5}, {6}, {7}, {8}, {5, 6}, {5, 7}, {5, 8}, {6, 7}, {6, 8}, {7, 8}, {5, 6, 7}, {5, 6, 8}, {5, 7, 8}, {6, 7, 8},
For such more questions on Power Sets Examples for Sets
https://brainly.com/question/33026825
#SPJ8
1. If 5tanA=4, Find the value of (5sinA-3cosA)/(4cosA+5sinA)
2. Solve for θ, sinθ/(1+cosθ) + (1+cosθ)/sinθ =4, 0°<θ<90°
3. Prove that tan〖θ-cotθ 〗 = (〖2sin〗^2 θ-1)/sinθcosθ
4. Without using trigonometric tables ,show that
tan 10°tan15°tan75°tan80°=1
5. If x=acosθ-bsinθ and y=asinθ + bcosθ prove that x^2+y^2=a^2+b^2
Answers
Answer:
1. (5·sin(A) - 3·cos(A)/(4·cos(A) + 5·sin(A)) = 1/8
2. θ = 30°
3. tan(θ) - cot(θ) = (2·sin²(θ) -1)/((cos(θ)×sin(θ))
from tan(θ) - 1/tan(θ) = sin(θ)/cos(θ) - cos(θ)/sin(θ) and sin²(θ) + cos²(θ) = 1
4. tan10°·tan15°·tan75°·tan80°= 1 from;
sin(α)·sin(β) = 1/2[cos(α - β) - cos(α + β)]
cos(α)·cos(β) = 1/2[cos(α - β) + cos(α + β)]
5. x² + y² = a² + b² where x = a·cosθ - b·sinθ and y = a·sinθ + b·cosθ from;
cos²θ + sin²θ = 1
Step-by-step explanation:
1. Here we have 5·tan(A) = 5·sin(A)/cos(A) = 4
∴ 5·sin(A) = 4·cos(A)
Hence to find the value of (5·sin(A) - 3·cos(A)/(4·cos(A) + 5·sin(A)) we have;
Substituting the value for 5·sin(A) = 4·cos(A) into the above equation in both the numerator and denominator we have;
(4·cos(A) - 3·cos(A)/(4·cos(A) + 4·cos(A)) = cos(A)/(8·cos(A)) = 1/8
Therefore, (5·sin(A) - 3·cos(A)/(4·cos(A) + 5·sin(A)) = 1/8
2. For the equation as follows, we have
\(\frac{sin \theta}{1 + cos \theta} + \frac{1 + cos \theta}{sin \theta} = 4\) this gives
\(\frac{2sin (\theta/2) cos (\theta/2) }{2 cos^2 (\theta/2)} + \frac{2 cos^2 (\theta/2)}{2sin (\theta/2) cos (\theta/2) } = 4\)
\(tan\frac{\theta}{2} + \frac{1}{tan\frac{\theta}{2} } = 4\)
\(tan^2\frac{\theta}{2} + 1 = 4\times tan\frac{\theta}{2}\)
\(tan^2\frac{\theta}{2} - 4\cdot tan\frac{\theta}{2} + 1 = 0\)
We place;
\(tan\frac{\theta}{2} = x\)
∴ x² - 4·x + 1 = 0
Factorizing we have
(x - (2 - √3))·(x - (2 + √3))
Therefore, tan(θ/2) = (2 - √3) or (2 + √3)
Solving, we have;
θ/2 = tan⁻¹(2 - √3) or tan⁻¹(2 + √3)
Which gives, θ/2 = 15° or 75°
Hence, θ = 30° or 150°
Since 0° < θ < 90°, therefore, θ = 30°
3. We have tan(θ) - cot(θ) = tan(θ) - 1/tan(θ)
Hence, tan(θ) - 1/tan(θ) = sin(θ)/cos(θ) - cos(θ)/sin(θ)
∴ tan(θ) - 1/tan(θ) = (sin²(θ) - cos²(θ))/(cos(θ)×sin(θ))...........(1)
From sin²(θ) + cos²(θ) = 1, we have;
cos²(θ) = 1 - sin²(θ), substituting the value of sin²(θ) in the equation (1) above, we have;
(sin²(θ) - (1 - sin²(θ)))/(cos(θ)×sin(θ)) = (2·sin²(θ) -1)/((cos(θ)×sin(θ))
Therefore;
tan(θ) - cot(θ) = (2·sin²(θ) -1)/((cos(θ)×sin(θ))
4. tan10°·tan15°·tan75°·tan80°= 1
Here we have since;
sin(α)·sin(β) = 1/2[cos(α - β) - cos(α + β)]
cos(α)·cos(β) = 1/2[cos(α - β) + cos(α + β)]
Then;
tan 10°·tan15°·tan75°·tan80° = tan 10°·tan80°·tan15°·tan75°
tan 10°·tan80°·tan15°·tan75° = \(\frac{sin(10^{\circ})}{cos(10^{\circ})} \times \frac{sin(80^{\circ})}{cos(80^{\circ})} \times \frac{sin(15^{\circ})}{cos(15^{\circ})} \times \frac{sin(75^{\circ})}{cos(75^{\circ})}\)
Which gives;
\(\frac{sin(10^{\circ}) \cdot sin(80^{\circ})}{cos(10^{\circ})\cdot cos(80^{\circ})} \times \frac{sin(15^{\circ}) \cdot sin(75^{\circ})}{cos(15^{\circ})\cdot cos(75^{\circ})}\)
\(=\frac{1/2[cos(80 - 10) - cos(80 + 10)]}{1/2[cos(80 - 10) + cos(80 + 10)]} \times \frac{1/2[cos(75 - 15) - cos(75 + 15)]}{1/2[cos(75 - 15) + cos(75 + 15)]}\)
\(=\frac{1/2[cos(70) - cos(90)]}{1/2[cos(70) + cos(90)]} \times \frac{1/2[cos(60) - cos(90)]}{1/2[cos(60) + cos(90)]}\)
\(=\frac{[cos(70)]}{[cos(70) ]} \times \frac{[cos(60)]}{[cos(60) ]} =1\)
5. If x = a·cosθ - b·sinθ and y = a·sinθ + b·cosθ
∴ x² + y² = (a·cosθ - b·sinθ)² + (a·sinθ + b·cosθ)²
= a²·cos²θ - 2·a·cosθ·b·sinθ +b²·sin²θ + a²·sin²θ + 2·a·sinθ·b·cosθ + b²·cos²θ
= a²·cos²θ + b²·sin²θ + a²·sin²θ + b²·cos²θ
= a²·cos²θ + b²·cos²θ + b²·sin²θ + a²·sin²θ
= (a² + b²)·cos²θ + (a² + b²)·sin²θ
= (a² + b²)·(cos²θ + sin²θ) since cos²θ + sin²θ = 1, we have
= (a² + b²)×1 = a² + b²
i choose a random integer n between $1 and $10 inclusive what is the probability that for the n i chose there exist no real solutions to the equation x x 5 n express your answer as a common fraction
Answers
The probability that for a randomly chosen integer n between 1 and 10 inclusive there exist no real solutions to the equation x^2 + 5 = n is 3/10.
we can first find the values of n for which there are real solutions to the equation x^2 + 5 = n. We can do this by rearranging the equation to get x^2 = n - 5 and then seeing that there are real solutions only if n - 5 is non-negative, i.e. n >= 5.
Since we are choosing a random integer between 1 and 10 inclusive, there are 10 possible values for n. Out of these, only 5, 6, 7, 8, 9, and 10 are greater than or equal to 5, which means that there are real solutions to the equation for these values of n. Therefore, there are only 6 possible values of n for which there exist no real solutions to the equation.
Therefore, the probability of choosing one of these 6 values of n is 6/10, which simplifies to 3/5. However, we need to find the probability of choosing one of the values of n for which there exist no real solutions to the equation, which is the complement of the probability of choosing one of the values of n for which there are real solutions. This complement is 1 - 6/10, which simplifies to 2/5.
Therefore, the main answer to the question is that the probability that for a randomly chosen integer n between 1 and 10 inclusive there exist no real solutions to the equation x^2 + 5 = n is 2/5.
The probability that for a randomly chosen integer n between 1 and 10 inclusive there exist no real solutions to the equation x^2 + 5 = n is 2/5. This can be found by first determining the values of n for which there are real solutions to the equation, and then finding the complement of this probability.
To know more about equation test visit:
https://brainly.com/question/29657983
#SPJ11
Write the equation of a line (y=mx+b) that passes through the points.
(2, 3) and 4. 4)
Answers
Answer:
Step-by-step explanation:
slope: (4-4)/(4-3)
slope: y=x+c
4=4+C
4-4=c
0=c
so y=x
4-2=2
X=1/2
Y=Mx+b
4=1/2(4)+b
4=2+b
2=b
Y=1/2x+2
2. cost to store: $25
markup: %
selling price: $45
Answers
Answer:
95
Step-by-step explanation:
you take the 25x2 and add the sellong price. Bada bing bada boom you get $95
A straw is placed inside a rectangular box that is 6 inches by 4 inches by 7 inches, as shown. If the straw fits exactly into the box diagonally from the bottom left corner to the top right back corner, how long is the straw? Leave your answer in the simplest radical form.
Answers
The length of the straw is √101 inches
How to find the length of the straw?The rectangular box has:
length (l) = 6 inches
breadth (b) = 4 inches
height (h) = 7 inches
The straw is said to fit into the box diagonally from the bottom.
So, the length of the straw is calculated as:
S= √(l² + b² + h²)
S = √(6² + 4² + 7²)
S = √101 inches
Learn more about rectangles on:
https://brainly.com/question/17297081
#SPJ1
The length of two sides of a right triangle are leg: 9 m and hypotenuse: 15 m. Find the length of the third side.
Answers
Answer:
Length of Third Side = 12 m
Step-by-step explanation:
You can use the Pythagorean Theorem to solve this: a² + b² = c² or c² - b² = a² in which a and b are legs, and c is the hypotenuse. We use the second equation to solve this: 15² - 9² = a² or 225 - 81 = a². This simplifies to 144 = a². To find a specifically, find the square root of 144, 12.
Hope it helps!
Tell me the answers pls :)
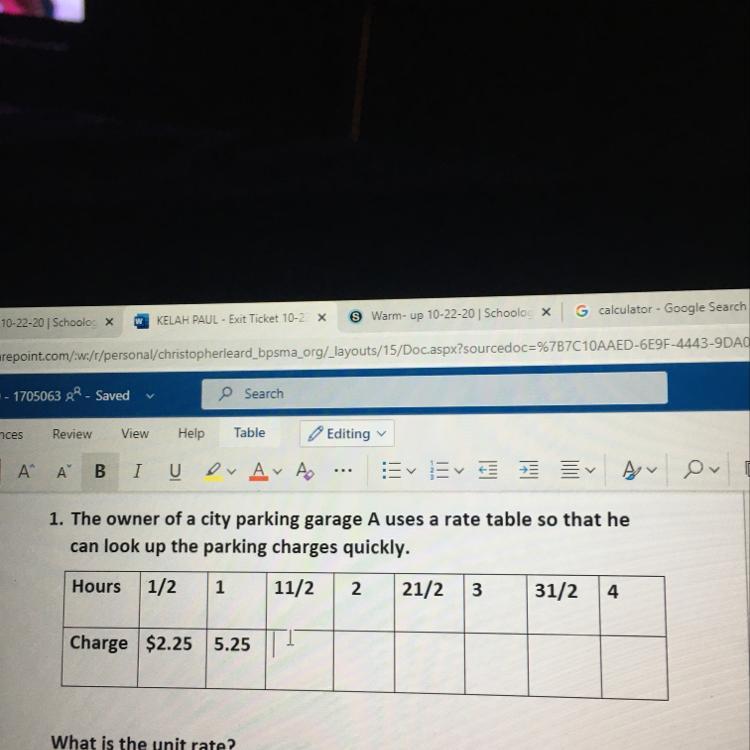
Answers
KAYLA WALKS 3 2/5 MILES EACH DAY. HOW FAR WILL SHE WALK IN 7 DAYS?
Answers
Answer:
23.8 Miles in 7 days
Step-by-step explanation:
Answer:
In 7 days Kayla will walk 23 4/5 miles.
Step-by-step explanation:
3.4*7= 23.8 = 23 4/5
3 2/5 = 17/5 17/5*7= 119/5 = 23.8
A full glass of water can hold 1/6 of a bottle
How many glasses of water can be filled with 3 1/2 of water
Answers
Answer:
21
Step-by-step explanation:
Well you basically divide 3 and 1/2 by 1/6 which you would you have to simplify the 3 and 1/2 which is 7/2 and switch the denominator and numerator of the 1/6 which would be 6/1 and after you multiply(7/2 x 6/1=42/2) it would be 42/2 which you would have to simplify by dividing 42 and 2 which is 21. There you go I hope this helps.
Answer:
21.
Step-by-step explanation:
That would be 3 1/2 divided by 1/6.
= 7/2 / 1/6
= 7/2 * 6
= 42/2
= 21 glasses.
Reflect the triangle over the y-axis and find the coordinate of the image of point K.
K’(2, 1)
K’(–2, 1)
K’(–2, –1)
K’(2, –1)
Answers
K'(-2, 1) is the coordinate of the image of point K, found by multiplying the original x-coordinate of the point K (2) by -1. To reflect the triangle over the y-axis, the x-coordinate of each point is multiplied by -1.
What is triangle?Triangle is a three-sided geometric shape which has three angles and three sides. The three sides of a triangle are typically referred to as the base, the height, and the hypotenuse. A triangle can be classified as either right, obtuse, or acute depending on the measure of its angles. Right triangles have one right angle, obtuse triangles have one obtuse angle, and acute triangles have three acute angles.
The coordinate of the image of point K is K’(-2, 1). This means that the x-coordinate of the point is -2 and the y-coordinate of the point is 1. This can be found by multiplying the original x-coordinate of the point K (2) by -1. The y-coordinate of point K remains the same, so the y-coordinate of the image of point K is 1.
Therefore, the coordinate of the image of point K is K’(-2, 1).
To know more about triangle click-
brainly.com/question/17335144
#SPJ1