What did the firefly say as the sun set algebraic expression?
Answers
a. eight more than the number: 8+n (14D)
b. three times the number: 3n (15V)
c. the product of the number and eight: 8n (5B)
d. three less than the number: n-3 (8S)
e. three decreased by the number: 3-n (1R)
Crossed out: 14D, 15V, 5B, 8S, 1R.
To solve for "eight more than the number", you need to add 8 to the unknown number n, so the algebraic expression is n+8. Therefore, you should cross out 14D, as it represents 8 added to n. To solve for "three times the number", you need to multiply the unknown number n by 3, so the algebraic expression is 3n. Therefore, you should cross out 15V, as it represents 3 multiplied by n.
To solve for "the product of the number and eight", you need to multiply the unknown number n by 8, so the algebraic expression is 8n. Therefore, you should cross out 5B, as it represents 8 multiplied by n. To solve for "three less than the number", you need to subtract 3 from the unknown number n, so the algebraic expression is n-3. Therefore, you should cross out 8S, as it represents n minus 3.
To solve for "three decreased by the number", you need to subtract the unknown number n from 3, so the algebraic expression is 3-n. Therefore, you should cross out 1R, as it represents 3 minus n.
To know more about algebraic expression, here
https://brainly.com/question/28884894
#SPJ4
--The complete question is, What Did the Firefly Say as the Sun Set?
Write an algebraic expression for the phrase. Cross out the number-letter pair above each correct answer. For each number-letter pair that you DON'T cross out, write the letter in the matching numbered box at the bottom of the page.
1. Let n represent an unknown number.
a. eight more than the number
b. three times the number
c. the product of the number and eight
d. three less than the number
e. three decreased by the number
8n (5B)
8-n (2O)
8+n (14D)
3-n (1R)
3n (15V)
n-3 (8S)
n+3 (11W)--
Related Questions
Find the z-score for the value 62, when the mean is 79 and the standard deviation is 4. Select one:
A. z = -4.50
B. z = 0.73
C. z = -0.73
D. z = -4.25
Answers
Answer: D.
Step-by-step explanation:
The formula for a z-score in statistics is:
(x-value - mean) / standard deviation
We are given all three values, so we can simply plug them in:
z = (62 - 79)/4
z = -17/4
z = -4.25
Click on the picture which is the answer ?

Answers
Answer:
L = 4πa²b
Step-by-step explanation:
Multiply both sides by 4πa²b.
Can you please help me with these problems, I just don't really understand how to calculate the area of these types of shapes.
thank you!
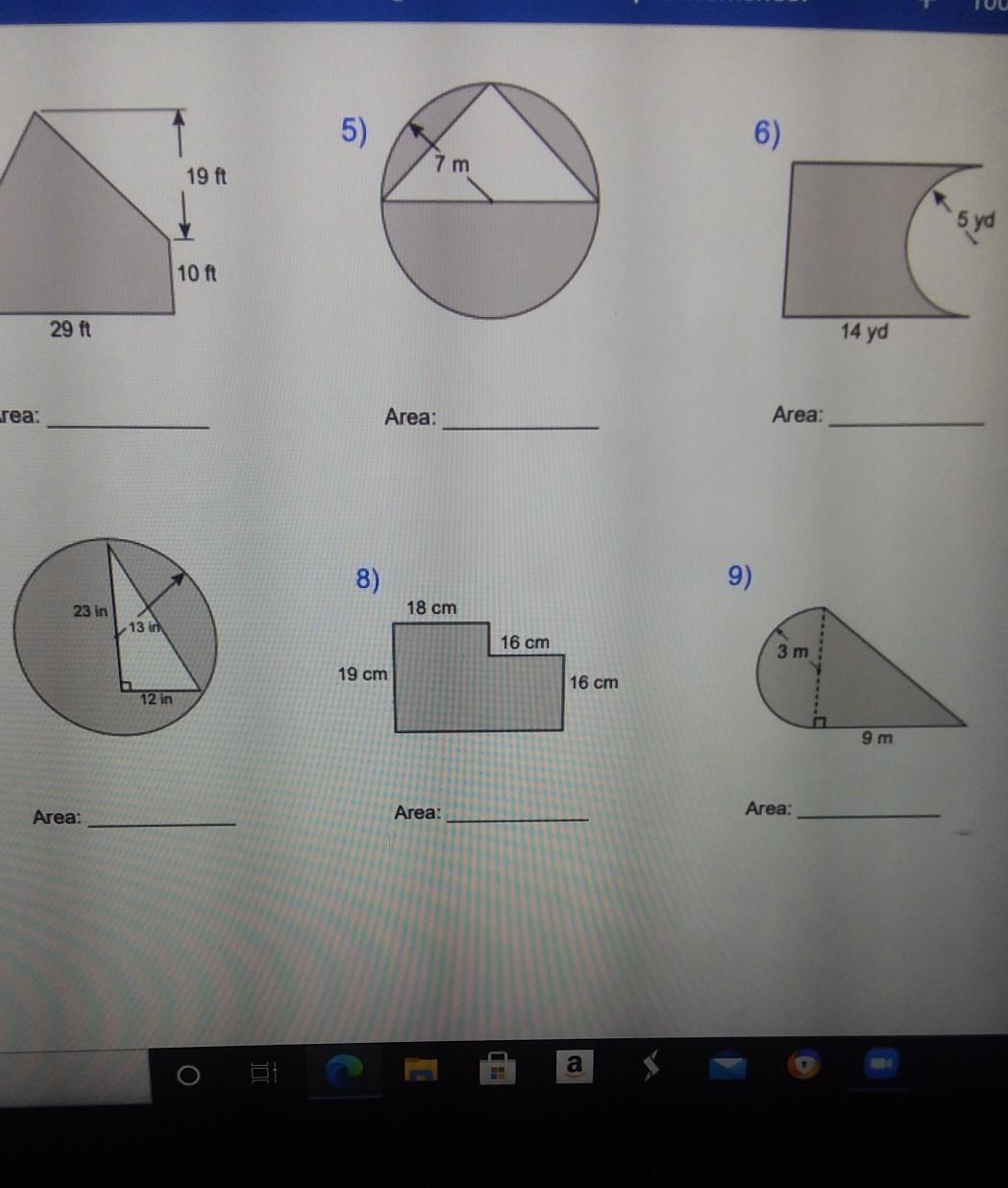
Answers
4. Not enough info, the shape is cut off. Are there 4 sides or 5? If there's a 5th side, is it slanted or parallel to the one labeled 10 ft?
5. The circle has a radius of 7 m, so its area is
π (7 m)² = 49π m²
Subtract from this the area of the white triangle. It has a base length equal to the diameter (i.e. twice the radius) of the circle, and a height equal to the radius, so its area is
1/2 (14 m) (7 m) = 49 m²
So the area of the shaded region is (49π - 49) m², or 49 (π - 1) m².
6. The rectangle has length 14 yd and height equal to the diameter of the circular cutout, 10 yd, so its area is
(14 yd) (10 yd) = 140 yd²
The circular cutout is a semicircle with radius 5 yd, so its area is
1/2 π (5 yd)² = 25π/2 yd²
Then the area of the shaded region is (140 - 25π/2) yd², or 1/2 (280 - 25π) yd².
7. The circle has radius 13 in, so its area is
π (13 in)² = 169π in²
The triangle has height 23 in and length 12 in, so its area is
1/2 (23 in) (12 in) = 138 in²
Then the area of the shaded region is (169π - 138) in².
8. The shaded region is a rectangle with a smaller rectangular cutout. The larger rectangle has height 19 cm and length 18 cm + 16 cm = 34 cm, so its area is
(19 cm) (34 cm) = 646 cm²
The smaller rectangular cutout has length 16 cm and height 19 cm - 16 cm = 3 cm, so its area is
(16 cm) (3 cm) = 48 cm²
Then the area of the shaded region is 646 cm² - 48 cm² = 598 cm².
9. The semicircular piece has radius 3 m, so its area is
1/2 π (3 m)² = 9π/2 m²
The triangle has height equal to the semicircle's diameter, 6 m, and length 9 m, so its area is
1/2 (6 m) (9 m) = 27 m²
Then the area of the shaded region is (9π/2 + 27) m², or 1/2 (9π + 54) m².
a team of swimmer is training for a swim meet. the table shows the number of laps each person has swum sk far and how long the laps took
Answers
According to the information it can be inferred that Jonathan and Seth have the same ratio of laps and time.
How to find the pair of swimmers that has the same ratio of time and laps?To find the pair of swimmers that has the same ratio of time to laps we must divide the time by the number of laps. Once we have done this procedure, we compare the results and establish which couple has the same result; that will be the couple that has the same ratio.
4 / 2 = 21 / 1 = 16 / 3 = 221 / 7 = 37 / 4 = 1.75Based on the above, we can infer that Seth or Jonathan have the same ratio of time and laps.
Note: This question is incomplete. Here is the complete information:
Name Laps Time (minutes)
Jonathan 2 4Julian 1 1Seth 3 6Bennett 7 21Taylor 4 7The relationship between time and the number of laps is not proportional across all swimmers. Which two swimmers swam at the same rate (had time and laps in the same proportion)?
Learn more about swimming pool in: https://brainly.com/question/13639763
#SPJ1
Help me pleaseeeee
Thank you

Answers
Answer:
\((x - 3)^2 + (y + 2)^2 = 41\)
Step-by-step explanation:
The general shape of the equation is:
(x-a)² + (y-b)² = r²
Where (a,b) is the center and r is the radius.
(a,b) = (3,-2) is given.
To find the radius r, or even simpler, r², calculate the distance between (-3,2) and (8,2) using pythagoras.
r² = (8-3)² + (2--2)² = 41
Write two numbers that multiply to the value on top and add to value on bottom.

Answers
Explanation: 9•5=45 , 9+5=14
One positive number is 6 times another number. The difference between the two numbers is 205. Find the numbers. (Enter your answers as a comma-separated list.)
Answers
Answer:
Hence the positive numbers are 246, and 41
(246, 41)
Step-by-step explanation:
From the question,
One positive number is 6 times another numberLet the first positve number be \(x\)
and the other number be \(y\)
Hence,
\(x = 6y\) ....... (1)
Also,
The difference between the two numbers is 205That is,
\(x - y =205\) ........(2).
To solve for the two unknowns, substitute the value of \(x\) in equation (1) into equation (2).
Since,
\(x = 6y\)
Then
\(x - y =205\) becomes
\((6y) - y =205\\\)
Then,
\(6y - y = 205\\5y = 205\\\)
Divide both sides by 5
\(\frac{5y}{5} = \frac{205}{5} \\ y = 41\\\)
∴ the value of \(y\) is 41
Now, substitute the value of y into equation (1) to find \(x\)
Then,
\(x = 6y\) becomes
\(x = 6(41)\\x = 246\\\)
∴ the value of \(x\) is 246
Hence the positive numbers are 246, and 41
(246, 41)
NEED HELP ASAP, WILL GIVE BRAINLIEST!!
In the figure shown, angle 1 has a measure of 90° and angle 2 has measure of 38°. Using angles 4, 3, and 2 write an equation and solve for angle 3. Then solve for angle 6 & 5.
Equation for Angle 3-
Angle 3=
Angle 5=
Angle 6=

Answers
*2=5=38*
1+2+3+4+5+6=360
(90)+(30)+3+(90)+(38)+6=360
3+6=114
3=6
*3=57*
*6=57*
Answer:
Equation for Angle 3- 90-38=52
Angle 3= 52
Angle 5= 38
Angle 6= 52
Step-by-step explanation:
Angle is 90 degrees.
Angle 2 is 38 degrees.
If you are just looking at the bottom half(Angle 6, Angle 1, and Angle 2) They are all supposed to add up to equal 180 degrees because it is a supplementary angle.
So you add 90 and 38 and it gives you 52(Angle 6).
90+38+52=180
Then a complementary angle is two angles that equal 90 degrees.
So if you take Angle 2(38 degrees) and subtract it from 90, you get 52. Which is Angle 3.
You do the same with Angle 6 and Angle 5.
Angle 6(52 degrees) subtract from 90 and you get 38.
Then you add 38 and 52 and you get 90.
Then 180-90=90, so Angle 4 is 90 degrees.
15 points! Solve for x
(sqrt{2}+1)^x +(sqrt{2}-1)^x = 6.
Answers
Answer: x = 5.2136 or x = -1.2136
Step-by-step explanation: Let's first simplify the expression by using the identity:
(a+b)^2 = a^2 + 2ab + b^2
For this problem, let a = sqrt(2) and b = 1, so we get:
(sqrt{2}+1)^2 = 2 + 2sqrt{2} + 1 = 3 + 2sqrt{2}
Now we can rewrite the original equation as:
(sqrt{2}+1)^x + (sqrt{2}-1)^x = 6
[(sqrt{2}+1)^(x/2)]^2 + [(sqrt{2}-1)^(x/2)]^2 + 2(sqrt{2}+1)^(x/2)(sqrt{2}-1)^(x/2) = 6
Let's define a = (sqrt{2}+1)^(x/2) and b = (sqrt{2}-1)^(x/2), then the equation can be rewritten as:
a^2 + b^2 + 2ab = 6
Now we can substitute the value we found earlier for (sqrt{2}+1)^2:
a^2 + b^2 + 2ab = 3 + 2sqrt{2}
We can rewrite this as:
(a+b)^2 = 3 + 2sqrt{2}
Taking the square root of both sides, we get:
a+b = ±√(3 + 2sqrt{2})
Now we can substitute back in the expressions for a and b:
(sqrt{2}+1)^(x/2) + (sqrt{2}-1)^(x/2) = ±√(3 + 2sqrt{2})
We can solve for x/2 by taking the logarithm of both sides:
log[(sqrt{2}+1)^(x/2) + (sqrt{2}-1)^(x/2)] = log[±√(3 + 2sqrt{2})]
x/2 = 2.6068 or -0.6068
Multiplying both sides by 2, we get:
x = 5.2136 or -1.2136
Therefore, the solutions are:
x = 5.2136 or x = -1.2136.
6261 Find the dual of the following primal problem [5M Minimize z = 60x₁ + 10x₂ + 20x3 Subject to 3x₁ + x₂ + x3 ≥ 2 1₁-22 +1 21 X₁ + 2X₂ − X3 ≥ 1, X1 X2 X3 20.
Answers
The given primal problem is a linear programming problem with a minimization objective function and a set of linear constraints. To find the dual of the primal problem, we will convert it into its dual form by interchanging the roles of variables and constraints.
The given primal problem can be rewritten in standard form as follows:
Minimize z = 60x₁ + 10x₂ + 20x₃
Subject to:
3x₁ + x₂ + x₃ ≥ 2
x₁ - 2x₂ + x₃ ≥ 1
x₁ + 2x₂ - x₃ ≥ 1
x₁, x₂, x₃ ≥ 0
To find the dual problem, we introduce dual variables y₁, y₂, and y₃ corresponding to each constraint.
The dual objective function is to maximize the dual objective z, given by:
z = 2y₁ + y₂ + y₃
The dual constraints are formed by taking the coefficients of the primal variables in the objective function as the coefficients of the dual variables in the dual constraints. Thus, the dual constraints are:
3y₁ - y₂ + 2y₃ ≤ 60
y₁ + 2y₂ + y₃ ≤ 10
y₁ + y₂ - y₃ ≤ 20
The variables y₁, y₂, and y₃ are unrestricted in sign since the primal problem has non-negativity constraints.
Therefore, the dual problem can be summarized as follows:
Maximize z = 2y₁ + y₂ + y₃
Subject to:
3y₁ - y₂ + 2y₃ ≤ 60
y₁ + 2y₂ + y₃ ≤ 10
y₁ + y₂ - y₃ ≤ 20
In conclusion, the dual problem of the given primal problem involves maximizing the dual objective function z subject to a set of dual constraints.
The dual variables y₁, y₂, and y₃ correspond to the primal constraints, and the objective is to maximize z.
To learn more about dual problem visit:
brainly.com/question/32193917
#SPJ11
Question 1
8 pts
1) Drew is an artist. He paints portraits. The table below
shows the number of portraits painted in hours. Do the
numbers in the table represent a proportional relationship?
Number of portraits Time (In Hours)
1
5
2
10
3
15
4.
20
WN
yes
no
No answer text provided.
No answer text provided.
Answers
Answer: Yes
If you notice, you can actually see that each number is multiplied by 5:
1 x 5 = 52 x 5 = 103 x 5 = 154 x 5 = 20Hope this helps you!
PLS HELP IM GONNA CRY ONG

Answers
Step-by-step explanation:
Question:To find value of sGiven Equation:\( \frac{s - 2}{s} = \frac{53}{55} \)Solution:\( = > \frac{s - 2}{s} = \frac{53}{55} \)
On cross multiplication=> 55(s - 2) = 53 × s
On Simplification=> 55s - 110 = 53s
Putting like terms on one side=> 55s - 53s = 110
On Simplification=> 2s = 110
Dividing both sides by 2\( = > \frac{2s}{2} = \frac{110}{2} \)
On Simplification=> s = 55 (Ans)
Then you cross multiply
55s-110=53s
= 2s=110
Therefore s=55
PLS DO NUMBER 9 WILL MARK BRAINLY AND ALSO GIVE AN ADDITIONAL 100 PTS IF CORRECT PLS HURRY. THANK YOU

Answers
Answer: 340
There's 7 days in a week. Meaning that you have to do 45 x 7 which is 315. since theres a 25 dollar gps fee you have to add 315 to 25 which is equal to 340
I will give branliest if you answer all four questions!

Answers
Answer:
3- 0
there's 8 rows, and 48 tiles, 48/8=6, so there's no purple tiles needed
4- 240
36 students + 4 adults = 40, 40 people times 6 full buses = 240 people in total
5- 12
72 flags divided by 6 flags in each row = 12 rows
6- 10, 24, 38
composite numbers are like the opposite of prime numbers, you can divide them by more than just themselves and 1
hope this helps :)
3.) 24 (im not exactly sure)
4.) 240
5.) 12
6.) 10, 24, 38
At 98°F, a certain insect chirps at a rate of 88 times per minute, and at 107°F, they chirp 151 times per minute. Write an equation in slope-intercept form that represents the situation.
Answers
The equation in slope-intercept form that represents the situation is y = 7x - 598
What is slope?The slope of a line is the ratio of the amount that y increases as x increases some amount. Slope tells you how steep a line is, or how much y increases as x increases. The slope is constant (the same) anywhere on the line.
The ordered pair are ( 98, 88) and (107, 151)
Equation of line in slope-intercept form is y = mx + c
at x = 98, y =88
so that by substituting we have,
88 = 98m + c -------------------1
at x = 107, y = 151 and by substituting we have
151 = 107m + c -----------------2
subtract equation 1 from 2
63 = 9m
m = 63/9
m = 7
substitute m = 7 in equation 1
88 = 98(7) + c
c = 88 - 686c
c = -598
substitute m and c for their values equation becomes
y = 7x - 598
In conclusion, the equation in slope-intercept form is y = 7x - 598
Learn more about slope: https://brainly.com/question/3493733
#SPJ1
Solve for r.
21 = 42 - 3r
A. r = -8
B. r = -7
C. r = 7
D. r = 8
Answers
Answer:7
Step-by-step explanation:
21=42-3r
21-42=3r
-21=3r
r=7
Answer:
-7
Step-by-step explanation:
Part A
Rewrite 0.5 as an exponential expression with a base of 2.
Answers
Answer:
\(2^{-1}\)
Explanation:
05/10
Simplifying
1/2
or 2^-1
Hope this helps you. Do mark me as brainlist
Mrs. Hamilton shows her students this graph and asks them to determine how figure A was transformed to figure B.
On a coordinate plane, triangle A has points (negative 1, 0), (negative 2, 4), (negative 1, 4). Triangle B has points (3, 1), (3, 5), (4, 5)..
Marcus suggests that figure A was reflected over the y-axis and then translated 2 to the right and 1 up. Julianne agrees, and states that the transformations could happen in any order. Which best describes the accuracy of Julianne’s statement?
Accurate. A translation of figure A of 2 to the right and 1 up and then a reflection over the y-axis produces the image, figure B.
Accurate. A reflection over the y-axis and then a translation of 1 up and 2 to the right produces the image, figure B.
Inaccurate. A translation of 2 to the right and 1 up and then a reflection over the y-axis results in a figure that is located in the second quadrant.
Inaccurate. A reflection over the y-axis and then a translation of 1 up and 2 to the right results in a figure that is located in the second quadrant.
Answers
Using translation concepts, it is found that the correct statement is:
Accurate. A reflection over the y-axis and then a translation of 1 up and 2 to the right produces the image, figure B.What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
In this problem, the points on triangle A are: (-1, 0), (-2, 4) and (-1, 4).
Marcus' translation is as follows:
Reflection over the y-axis, hence \(x \rightarrow - x\), and the points are: (1,0), (2,4) and (1,4).2 units to the right, hence \(x \rightarrow x + 2\), then the points are: (3, 0), (4,4) and (3,4).1 unit up, hence \(y \rightarrorw y + 1\), and the points are (3,1), (4,5) and (3,5).The points are the same of triangle B, hence the statement is accurate. According to the order of the translations, the second statement is correct.You can learn more about translation concepts at https://brainly.com/question/4521517
Answer:
A
Step-by-step explanation:
The sum of the measures of two angles is 140 degrees. The ratio of their measures is 3:4.
Answers
Answer: The measurement of the first angle would be 60 degrees and the second angle would be 80 degrees.
Step-by-step explanation: They both are equal to the ratio of 3:4 because 3 x 20 would be 60 and 4 x 20 is 80. When added together they would equal is 140 degrees.
Find value of x please

Answers
Answer:
C
Step-by-step explanation:
sinx=9/19
sinx=0.47
opposite function on calculator
x= ~28
Answer:
28˚
Step-by-step explanation:
If gasoline costs $ 3.77 per gallon when you pay with a credit card, but $0.08 per gallon less if you pay with cash, how much do you save by filling up a 8-gallon tank and paying for it with cash?
Answers
Answer:
$0.64
Step-by-step explanation:
Cost for 8 gallons of gas
Credit Card at $3.77/gal
Cash at $(3.77 - 0.08)/gal: $3.69/gal
(8 gal)*($3.77/gal) = $30.16
(8 gal)*($3.69/gal) = $29.52
Savings is $0.64
The power 9² is equivalent to 81. What is the value of 9-2? O-81 O O O 19
HELP PLSLELSLS

Answers
Answer:
The answer is C. 1/81
Step-by-step explanation:
Ralph’s average score for 5 tests was 82. on four of the tests his scores were 85, 73, 92, 66. what was the fifth test score?
Answers
Answer:
94
Step-by-step explanation:
Let the unknown number be denoted by the variable, x. Also note that, the average can be found by adding all values together and dividing by the amount of values there are.
Set the equation:
(85 + 73 + 92 + 66 + x)/5 = 82
Isolate the variable, x. Note the equal sign, what you do to one side, you do to the other. Simplify first by combining like terms, and then do the opposite of PEMDAS.
PEMDAS is the order of operations, and stands for:
Parenthesis
Exponents (& roots)
Multiplications
Divisions
Additions
Subtractions.
Combine like terms:
(85 + 73 + 92 + 66 + x)/5 = 82
(316 + x)/5 = 82
Next, isolate the x, by multiplying 5 to both sides of the equation:
(316 + x)/5 * 5 = (82) * 5
316 + x = 82 * 5
316 + x = 410
Lastly, subtract 316 from both sides of the equation:
x + 316 = 410
x + 316 (-316) = 410 (-316)
x = 410 - 316
x = 94
94 is the final test score.
Simplify each expression

Answers
Answer:
\(3. \: \: ( \frac{7}{8} ) ^{2} = \frac{ {7}^{2} }{ {8}^{2} } = \frac{49}{64} = 0.765 \)\(5. \: \: 8 + 5(7) = 8 + 35 = 43\)
I hope I helped you^_^
A hairdresser receives a discount on each comb purchased. The original price of each comb is x dollars. The hairdresser purchases 25 combs for a total of (25x-100) dollars. By how much is each comb discounted? $□?
Answers
Answer:
$4
Step-by-step explanation:
Original price of comb = x
Number of combs = 25
Amount paid after discount = (25x - 100)
From the expression :
Price of comb before discount : 25 * x
Discount on all 25 combs = 100
Discount on each comb = 100 / 25
= $4
2. Between which two weeks did the plant grow the least?
Answers
Answer:Probably the first week
Step-by-step explanation: It takes a while for a seed to get used to the dirt around it
If A is a 3 x 8 matrix, what is the minimum and maximum possible value of nullity(A)? The smallest possible value of nullity(A) is The largest possible value of nullity(A) is
Answers
The smallest possible value of nullity(A) is 0, and the largest possible value of nullity(A) is 8.
The nullity of a matrix is the dimension of its null space, which represents the set of vectors that satisfy the equation A * x = 0, where A is the matrix and x is a vector.
The nullity of a matrix can range from 0 to the number of columns in the matrix. In this case, since A is a 3 x 8 matrix, the minimum possible value of nullity(A) is 0, indicating that the null space is trivial and contains only the zero vector. This occurs when the matrix is full rank, meaning that its columns are linearly independent.
On the other hand, the maximum possible value of nullity(A) is 8, which would occur if the matrix has rank 0. In this case, all the columns of the matrix are linearly dependent, and the null space spans the entire vector space of size 8.
Therefore, the smallest possible value of nullity(A) is 0, and the largest possible value of nullity(A) is 8.
Learn more about nullity and rank of matrices here: brainly.com/question/31051373
#SPJ11
What is the average rate of change of the function from x = 1 to x = 3?

Answers
Answer: 10
Step-by-step explanation: you look at x=1 and go over to x=3 and do rise over run
Help aspp please thank you

Answers
The equation of the line would be y = (-3/4)x + 5.
What is the slope-point form of the line?
For the line having slope "m" and the point (x1, y1) the equation of the line passing through the point (x1, y1) having slope 'm' would be
y - y1 = m(x - x1)
The given equation is \(y=-\frac{3}{4}x-17\)
The required line is parallel to the given line.
and we know that the slopes of the parallel lines are equal so the slope of the required line would be m = -3/4
And the required line passes through (8, -1)
so by using slope - point form of the line,
y - (-1) = (-3/4)(x - 8)
y + 1 = (-3/4)x - (-3/4)8
y + 1 = (-3/4)x + 24/4
y = (-3/4)x + (12/2 - 1)
y = (-3/4)x + 5
Hence, the equation of the line would be y = (-3/4)x + 5.
To learn more about slope - point form of the line, visit:
https://brainly.com/question/24907633
#SPJ1
Find the solution to the initial value problem 2y
′′
−5y
′
−3y=0;y(0)=−3,y
′
(0)=1 and sketch a graph of the solution. Using a graphing utility for making sketches is fine, but you must show all work in determining the solution to receive credit.
Answers
The solution to the initial value problem 2y'' - 5y' - 3y = 0, with initial conditions y(0) = -3 and y'(0) = 1, is given by \(y(x) = 2e^{3*x}-3e^{-x}\) The graph of the solution will exhibit exponential growth and decay.
To solve the given initial value problem, we assume the solution has the form \(y(x)=e^{rx}\) and substitute it into the differential equation. We obtain the characteristic equation:
\(2r^{2} - 5r -3 =0\)
Factoring the quadratic equation, we get:
(2r + 1)(r - 3) = 0
Solving for r, we find two distinct roots: r = \(-\frac{1}{2}\) and r = 3.
Therefore, the general solution to the differential equation is given by:
\(y(x) = c_{1} e^{1/2x} + c_{2} e^{3x}\)
To find the particular solution, we use the initial conditions. Applying y(0) = -3, we have:
c₁ + c₂ = -3 (Equation 1)
Next, we differentiate y(x) to find y'(x):
\(y'(x) = -\frac{1}{2} c_{1} e^{-\frac{1}{2x} } + 3c_{2} e^{3x }\)
Applying y'(0) = 1, we have:
\(-\frac{1}{2} c_{1} + 3c_{2} =1\) (Equation 2)
Solving Equations 1 and 2 simultaneously, we find c₁ = -2 and c₂ = -1.
Therefore, the particular solution is:
\(y(x) = -2e^{(-1/2x)} - e^{3x}\)
Simplifying further, we get:
\(y(x)=2e^{3x}-3e^{-x}\)
The graph of the solution will exhibit exponential growth as the term \(2e^{3x}\) dominates and exponential decay as the term \(-3e^{-x}\) takes effect.
Learn more about differential equation here : https://brainly.com/question/32645495
#SPJ11