What are the example of exponential equation?
Answers
Exponential equation has tow major types
exponential decay
f(x) = a(1.16)^xexponential growth
f(x) = a(0.84)^xWhat are exponential equation?Exponent-based equations in which the exponent or a portion of the exponent is a variable are known as exponential equations.
This is a type of function that are of 3 main parts
the starting or initial value
base function
the exponents
Atypical example includes: f(x) = 300(1.16)^x
the starting = 300
the base = 1.16
the exponents = x
A mathematical function called an exponential function is employed frequently in everyday life. It is mostly used to compute investments, model populations, determine exponential decay or exponential growth, and so forth.
The base is what determines exponential growth or decay
Learn more about exponential function here:
https://brainly.com/question/29716012
#SPJ1
Related Questions
Please help it’s prb easy for u !!!!!!!!

Answers
Answer: The square
Step-by-step explanation:
The square has a 90 degree angle which is a right angle. Also all sides have the same length
The temperature at the point (X, y) on a metal plate is TX, y) = x/(x^2+y^2) Find the direction of greatest increase in heat from the point (1, 4).
Answers
The direction of greatest increase in heat from the point (1,4) is [15/17, -8/17].
The direction of greatest increase in heat at a point (x, y) on the metal plate is given by the gradient vector ∇T(x,y).
Let's first compute the partial derivatives of T(x,y) with respect to x and y:
∂T/∂x = \([(x^2+y^2) - 2x^2]/(x^2+y^2)^2 = (y^2-x^2)/(x^2+y^2)^2\)
∂T/∂y = \(-2xy/(x^2+y^2)^2\)
So the gradient vector ∇T(x,y) is:
∇T(x,y) = (∂T/∂x, ∂T/∂y) = \([(y^2-x^2)/(x^2+y^2)^2, -2xy/(x^2+y^2)^2]\)
At the point (1,4), we have:
∇T(1,4) = \([(4^2-1^2)/(1^2+4^2)^2, -2(1)(4)/(1^2+4^2)^2]\)= [15/625, -8/625]
So the direction of greatest increase in heat at (1,4) is the direction of the gradient vector ∇T(1,4), which is:
[15/625, -8/625] / \(\sqrt{[(15/625)^2 + (-8/625)^2] }\)= [15/17, -8/17]
Therefore, the direction of greatest increase in heat from the point (1,4) is [15/17, -8/17].
To learn more about gradient vector visit: https://brainly.com/question/29699363
#SPJ11
the diagonal of a parallelogram creates alternate interior angles. T/F
Answers
The given statement "The diagonal of a parallelogram does not create alternate interior angles" is false because alternate interior angles are formed when two parallel lines are intersected by a transversal, and they are located on opposite sides of the transversal and between the two parallel lines.
In a parallelogram, the opposite angles are congruent, meaning they have equal measures. When a diagonal is drawn in a parallelogram, it creates two pairs of congruent opposite angles, but these angles are not considered alternate interior angles.
To know more about parallelogram:
https://brainly.com/question/28854514
#SPJ4
Hugo has a brother and sister. Hugo is x years old. •
His sister Jasmine is 3 years older than Hugo •
His brother Manny is 2 years older than Jasmine.
Which expression represents the sum of the ages of Hugo and his two siblings?
x + 5
X + 8
3r + 5
3x + 8
pls help due soon
Answers
Answ
3xmas8
-------------------------------
listo
The volume of a cylinder is 4πx3 cubic units and its height is x units.
Which expression represents the radius of the cylinder, in units?
: 2x, 4x
Answers
Expression represents the radius of the cylinder, 2x units.
What is a cylinder?
A cylinder is simply a 3-dimensional shape having two parallel circular bases joined by a curved surface.
Given that:
Volume of cylinder =\(4\pi x^{3}\)
we know that, Volume of cylinder = \(\pi r^{2} h\)
\(4\pi x^{3}\)= π * \(r^{2}\) *h
\(4x^{3} = r^{2}*h\)
\(4x^{3} = r^{2}*x\) [since, height=x]
\(4x^{2} = r^{2}\)
r= 2x
Hence the radius of the cylinder is 2x units
Learn more cylinder here:
brainly.com/question/16788902
#SPJ1
Carina's farm owned some cows and goats. 20% of cows and 2/5 of the goats were sold this month. now carina owns equal number of cows and goats. if there are 480 cows and goats left, find how many goats and cows carina had owned originally.
Answers
Carina have 300 cows and 400 goats originally.
What is percentage?The Latin word "per centum," which meaning "by the hundred," was the source of the English word "percentage." Fractions with a denominator of 100 are called percentages. In other words, it is a relationship where the value of the entire is always assumed to be 100.A percentage is a certain number or part in every hundred. It is a fraction with the denominator 100, and the symbol for it is "%."for cows:
\(\frac{240}{(100-20)} =300\)
for goats:
\(\frac{240}{3} *5=400\)
Therefore, Carina have 300 cows and 400 goats originally.
To learn more about percentage, refer to
https://brainly.com/question/843074
#SPJ1
i have no clue what i’m doing

Answers
Answer:
c(x) = 16x + 22736
R(x) = -2x^2 + 524x
[ -2x^2 + 508x - 22736] = 0
Factored: f(x) = -2(x - 196)(x - 58)
58 to break even
Step-by-step explanation:
Your cost is the amount it cost you to "make" stuff.
You have fixed and variable costs (cost of oven is fixed cost of flower and sugar is variable to make cupcakes)
your cost is c(x) = 16x + 22736
"your oven and building cost $22736 per month and you use $16 worth of sugar butter flour to make one cupcake ( it must be a huge one) ...
your revenue is the amount of money that "comes into your business"...
the amount of money in the cash register.... Note: this is only money IN you still have to pay for the building, sugar flour etc.
R(x) = -2x^2 + 524x
Note: the minus and the square basically say that the more you charge the less cupcakes you will sell...
Profit is the money in minus the money out
P - R - E [ -2x^2 + 524x ] - [16x + 22736]
the break even point is where the two functions are the same
in other words where C=R or R-C=0
[ -2x^2 + 524x ] = [16x + 22736]
[ -2x^2 + 508x - 22736] = 0
Factored: f(x) = -2(x - 196)(x - 58)
Answer:
Step-by-step explanation:
C(x)=16x+22736
R(x)=-2x²+524x
P(x)=R(x)-C(x)
=-2x²+524x-16x-22736
=-2x²+508-22736
when profit is zero then no gain or loss.
so -2x²+508x-22736=0
or x²-254x+11368=0
196+58=254
196×58=11368
x²-54x-196x+11368=0
x(x-54)-196(x-54)=0
(x-54)(x-196)=0
x=54,196
so x=54 is the smallest number of bins to break even.
your chronometer is set for greenwich mean time (gmt or universal time, ut). high noon at your present location is 9 pm ut. what is your longitude?
Answers
Your longitude in DMS is 135 degree. So the option D is correct.
This is because there are 12 hours left in the local time ( i.e. 12 hours noontime or mid-day).
As UT (or GMT) time is 9 p.m., there are 9 hours between GMT time and local time.
9 hours = 9 × 60 minutes = 540 minutes
Now, we know that:
Every four minutes, the Earth turns one degree.
Thus, 1-degree longitude difference = 4 minutes
Or, 4 minutes of time difference = 1 degree of longitude
Or, 1 minute of time difference = 1/4 degree of longitude
Or, 540 minutes of time difference = (1/4) × 540 degrees of longitude
540 minutes of time difference = 135 degrees of longitude
Also, we can infer that the current location is in the Western hemisphere because we know that it is 9 hours behind GMT (or UT) time.
Hence, the longitude of the current location = 135⁰
So the option 4 is correct.
To learn more about longitude link is here
brainly.com/question/30926134
#SPJ4
The complete question is:
Your chronometer is set for Greenwich Mean Time (GMT or Universal Tim, UT). High noon at your present location is 9 pm UT. What is your longitude in DMS (not decimal degrees)?
1. 30° 18'W
2. 30° 16'W
3. 30° 17'W
4. none of the above
1. If f(x) = 6x + 13x + 2x - 5 and f(-1) = 0, find the
factors of f(x)
Answers
Answer:
-26
Step-by-step explanation:
Insert the f(-1) into the equation.It'll be f(-1) = 6(-1) + 13(-1) + 2(-1) - 5After you times all of it. You'll get 7-13-2-5Solve it and you'll get -26What is integral of sin 2
Answers
Sin 2 is the integral of -cos 2 plus c, where c is a constant integration equation sin2x dx = -cos2x + c.
1. Calculate sin 2 integral.
2. Apply the integration equation sin2x dx = -cos2x + c.
3. Increase the outcome by the constant C.
Sin 2 is the integral of -cos 2 plus c, where c is a constant. This integral must be calculated in several steps. Take the integral of sin 2 first. Use the integration formula sin2x dx = -cos2x + c to do this. According to this equation, the integral of sin 2 is equal to cos -2/c plus a certain constant. The next step is to add the constant c to the outcome after using this formula. This will result in the integral of sin 2 having a final value of -cos 2 + c. Any actual number may be used as the constant c, and the value will vary depending on the circumstances. It's crucial to keep in mind that the constant c must always be a part of the outcome.
Learn more about integral here
https://brainly.com/question/18125359
#SPJ4
Which problem is modeled?
0.8 – 0.5 = 0.3
0.08 – 0.03 = 0.05
0.8 – 0.3 = 0.5
0.08 – 0.05 = 0.03

Answers
Answer:
The answer is 0.8-0.3=0.5.
Hobby Lobby offered a 15% discount off the regular price of a lamp. The amount of the discount is $12. What is the regular price of the lamp?
Answers
12/0.15 = 80
Solution: regular price is $80
7 times what equals 12
Answers
Answer:
12/7Step-by-step explanation:
Let the required number be 'n'.
Then, we need to find what the value of n is.
According to the question,
7 x n = 12Multiply both sides by 1/7.
7 x n x 1/7 = 12 x 1/77/7 x n = 12/7n = 12/7-3(4x-3)-4(2x+5) =
someone please help easp
Answers
Answer:
-20x -11
Step-by-step explanation:
You want to simplify -3(4x-3)-4(2x+5).
SimplificationAn expression is simplified by removing parentheses and combining like terms. The parentheses are removed by making use of the distributive property.
-3(4x-3)-4(2x+5) . . . . . . . . . . . . given
= -3(4x) -3(-3) -4(2x) -4(5) . . . . use the distributive property
= -12x +9 -8x -20 . . . . . . . . . . . evaluate products
= (-12-8)x +(9 -20) . . . . . . . . . . group like terms
= -20x -11 . . . . . . . . . . . . . . . . evaluate sums
Differentiate the function. g(x)=3x ^−3 (x^4 −3x^3 +13x−9) g′ (x)=
Answers
The derivative of the function g(x) = 3x^(-3) (x^4 - 3x^3 + 13x - 9) is g'(x) = -9x + 12 + (27/x - 27/x^2 - 26/x^3), obtained by using the product rule and the chain rule.
To differentiate the function g(x) = 3x^(-3) (x^4 - 3x^3 + 13x - 9), we can use the product rule and the chain rule:
g'(x) = 3(-3x^(-4))(x^4 - 3x^3 + 13x - 9) + 3x^(-3)(4x^3 - 9x^2 + 13)
= -9x^(-4)(x^4 - 3x^3 + 13x - 9) + 3x^(-3)(4x^3 - 9x^2 + 13)
= (-9/x^4)(x^4 - 3x^3 + 13x - 9) + (3/x^3)(4x^3 - 9x^2 + 13)
= (-9x + 27/x - 39/x^3) + (12 - 27/x^2 + 13/x^3)
= -9x + 12 + (27/x - 27/x^2 - 26/x^3)
Therefore, the derivative of g(x) is g'(x) = -9x + 12 + (27/x - 27/x^2 - 26/x^3).
To know more about derivative, visit:
brainly.com/question/29144258
#SPJ11
Ms. Bacorn asked students in the seventh and eighth grades how much time, in minutes, they spend reading each day. These box plots show the results.
Based on the box plots, which statement is true?

Answers
The solution is: :
A. The range of both data sets is 40, this statement correctly describes the two data sets .
Here, we have,
we know that,
Range = the maximum value - the minimum value
For the Seventh-Grade Students' data set,
Maximum value = 45
Minimum Value = 5
Range = 45 - 5 = 40
For the Eight-Grade Students' data set,
Maximum value = 45 (the value at the whisker to your far right)
Minimum Value = 5 (value indivl ated by the whisker on your far left)
Range = 45 - 5 = 40
Therefore, the two data sets can be described as having the same range of 40.
To learn more on range click:
brainly.com/question/2622299
#SPJ1
complete question:
A school counselor asked a random sample of seventh- and eighth-
grade students how long it takes them to get ready for school each
morning. The dot plot and the box plot below summarize the results for
the two random samples. Which statement correctly describes the two
data sets below? *

the half-life of radon-222 is 3.8 days. a 34-gram sample of radon-222 is monitored for one day. how long will it take for the sample to be 15% of the initial amount? (rounded to the nearest hundredths)
Answers
It take 10.374 days for the sample to be 15% of the initial amount
Radioactivity decay half life formula:
N= \(N_{0} (\frac{1}{2} )^{t/t_{1/2} }\)
N = Quantity remaining
\(t_{1/2}\) = half life
t = time elapsed
\(N_{0}\) = initial amount
given,
Half-life of radon-222 is 3.8 days
\(t_{1/2}\) = 3.8 days
Initial amount of sample = 34 gm
15 % of 34 gm = 15 x 34 /100
= 5.1 gm
Quantity remaining = 5.1 gm
= 5.1 gm
Using the above formula
N= \(N_{0} (\frac{1}{2} )^{t/t_{1/2} }\)
5.1 = 34x \(0.5^{t/3.8}\)
\(0.5^{t/3.8}\) = 5.1/34
\(0.5^{t/3.8}\) = 0.15
taking ln both side
ln( \(0.5^{t/3.8}\) ) = ln (0.15 )
t/3.8 ln (0.5) = ln (0.15)
t/3.8 = ln (0.15) / ln (0.5)
= 2.73
t = 3.8 x 2.73 days
= 10.374 days
It take 10.374 days for the sample to be 15% of the initial amount.
To learn more about Radioactivity decay visit:https://brainly.com/question/1770619
#SPJ4
(-86)+(+83)
sfgghbhhhgh
Answers
-86 + 83 = -3
Hope this helps!
Draw a typical vertical section in the floor (By hand). Mark all the parts/sections by name.
Draw typical construction of a section width of the floor. Measure the thickness as well as possible.
What is basis for assumptions of insulation thickness.
Old floors will have significantly less insulation.
Answers
The typical vertical section of a floor includes the following parts/sections: finished floor, subfloor, insulation layer, vapor barrier, and structural support. Insulation thickness varies but is commonly around 1-2 inches.
In a typical floor section, the finished floor material (e.g., hardwood, carpet) has a thickness of about 0.25-0.75 inches. The subfloor, usually made of plywood or oriented strand board (OSB), is around 0.75 inches thick. The insulation layer, like rigid foam board, has a thickness of 1-2 inches. The vapor barrier, often made of polyethylene, has a thickness of 0.01-0.02 inches. The structural support, composed of joists or beams, varies based on the floor's load requirements. The assumption for insulation thickness is based on general construction practices, where 1-2 inches of insulation provides adequate thermal resistance for most buildings. Older floors may have thinner or no insulation due to outdated standards and less focus on energy efficiency.
A typical floor section consists of finished floor, subfloor, 1-2 inches of insulation, vapor barrier, and structural support. Insulation thickness is based on standard construction practices and may be reduced in older floors.
To know more about vertical visit:
https://brainly.com/question/30105258
#SPJ11
7y-4=17 what is the answer
Answers
Answer:
7y=21
y=21/7
y=3 answer
Answer:
y = 3
Step-by-step explanation:
Add 4 to each side, so it now looks like this: 7y = 21Divide each side by 7 to cancel out the 7 next to y. It should now look like this: y = 3I hope this helps!
; 3. Using the complex form, find the Fourier series of the function. (30%) 1, 2k – .25 < x < 2k +.25, k € Z. a. (15%), f (x) = 0, elsewhere S 1,0
Answers
The Fourier series Using the complex form of f(x) is
f(x) = 1/2 + ∑[n=1, ∞] [2*(-1)^(n+k)/(nπ)]*sin(nπx), 2k-0.25 < x < 2k+0.25
where k is an integer.
To find the Fourier series of the function f(x) over the interval [-1, 1], we first note that f(x) is periodic with period T = 0.5. We can then write f(x) as a Fourier series of the form
f(x) = a0/2 + ∑[n=1, ∞] (ancos(nπx) + bnsin(nπx))
where
a0 = (1/T) ∫[0,T] f(x) dx
an = (2/T) ∫[0,T] f(x)*cos(nπx) dx
bn = (2/T) ∫[0,T] f(x)*sin(nπx) dx
Since f(x) = 0 for x < -0.25 and x > 0.25, we only need to consider the interval [-0.25, 0.25]. We can break this interval into subintervals of length 0.5 centered at integer values k
[-0.25, 0.25] = [-0.25, 0.25] ∩ [1.5, 2.5] ∪ [-0.25, 0.25] ∩ [0.5, 1.5] ∪ ... ∪ [-0.25, 0.25] ∩ [-1.5, -0.5]
For each subinterval, the Fourier coefficients can be calculated as follows
a0 = (1/0.5) ∫[-0.25, 0.25] f(x) dx = 1/2
an = (2/0.5) ∫[-0.25, 0.25] f(x)*cos(nπx) dx = 0
bn = (2/0.5) ∫[-0.25, 0.25] f(x)sin(nπx) dx = 2(-1)^k/(nπ)
Therefore, the Fourier series of f(x) is
f(x) = 1/2 + ∑[n=1, ∞] [2*(-1)^(n+k)/(nπ)]*sin(nπx), 2k-0.25 < x < 2k+0.25
where k is an integer.
To know more about Fourier series of the function:
https://brainly.com/question/30621098
#SPJ4
Esgetteit give me a funney joek plox plox
Answers
Answer
why cant a orfian play baseball..... they dont know where home is.
Step-by-step explanation:
What is the decimal multiplier to increase by 6. 1%?
Answers
Answer: 1.061
Step-by-step explanation:
1). Based on conditions, formulate: 1+6.1%
2). Then convert to a decimal: 1.061
Groups A, B, and C have means of 4, 6, and 8, respectively. There are 15 cases in total, with equal sample sizes in each group. SSwithin is 120. 16-7. For 16-4a, what is omega-squared? 0 .12 0.25 d .33 O2
Answers
Groups A, B, and C have means of 4, 6, and 8, respectively. There are 15 cases in total, with equal sample sizes in each group. Within is 120. 16-7. 16-4a, the value of omega-squared is 0.25.
What is omega-squared?
In statistics, omega-squared is a measure of effect size that can be used for one-way ANOVA to determine how much variance is due to the treatment or independent variable. It is calculated by dividing the between-group variance by the total variance, which includes both the within-group and between-group variance.
Omega-squared is used to determine the percentage of variance accounted for by a particular factor or treatment. It is represented as ω2 and ranges from 0 to 1, with higher values indicating a stronger relationship between the independent variable and the dependent variable.
The formula for omega-squared is as follows:
ω2=SSBetween / SSTotalSSWithin
= SSTotal - SS Between
Where SSTotal is the sum of squares for the total variance.SSBetween is the sum of squares between the groups, and within is the sum of squares within the groups.
The given information is:
Mean of group A = 4Mean of group
B = 6Mean of group
C = 8Total cases
= 15SSWithin
= 120
We can calculate the sum of squares between the groups as follows:
SSTotal = SSBetween + SSWithinSSTotal
= (nA + nB + nC - 1) × (σA² + σB² + σC²)SSBetween
= SSTotal - SS Within SS Between
= (3 - 1) × (42 + 62 + 82) - 120SSBetween
= 80 Next,
we can calculate the total variance as:
SSTotal = SSWithin + SSBetweenSSTotal
= 120 + 80SSTotal
= 200
Now, we can calculate omega-squared as follows:
ω2 = SSBetween / SSTotalω2
= 80/200ω2
=0.4
Hence, the value of omega-squared is 0.25.
#SPJ11
Learn more about means and omega-squared at: https://brainly.com/question/14366264
he historical returns on a portfolio had an average return of 9 percent and a standard deviation of 13 percent. Assume that returns on this portfolio follow a bell-shaped distribution. What percentage of returns were greater than 22 percent? (Round your answer to the nearest whole percent.) Percentage of returns What percentage of returns were below -17 percent? (Round your answer to 1 decimal place.) Percentage of returns
Answers
The percentage of returns that were greater than 22% and the percentage of returns that were below -17% of historical returns on a portfolio that had an average return of 9 percent and a standard deviation of 13 percent.
What percentage of returns were greater than 22 percent? We know that returns on this portfolio follow a bell-shaped distribution and the percentage of returns greater than 22% is required.
The z-score for this value can be calculated as follows;
z=(X-μ)/σwhere X is the return percentage, μ is the average return percentage, and σ is the standard deviation.
z=(22-9)/13 = 1z = 1 gives a probability of 0.8413.
To calculate the percentage of returns greater than 22%, we need to subtract the z-score probability from 1;
P(z > 1) = 1 - 0.8413 = 0.158
The percentage of returns greater than 22% is therefore;
Percentage of returns greater than 22% = 0.1587 x 100 ≈ 16%2.
What percentage of returns were below -17 percent?
We need to find the percentage of returns that were below -17% using the same method as above;
z=(X-μ)/σz=(-17-9)/13 = -2z = -2 gives a probability of 0.0228.
To calculate the percentage of returns less than -17%, we need to add the z-score probability to 0.5 (since the bell-shaped curve is symmetric);
P(z < -2) = 0.5 + 0.0228 = 0.5228
The percentage of returns below -17% is therefore;Percentage of returns below -17% = 0.5228 x 100 ≈ 52.3%
Thus, the percentage of returns that were greater than 22 percent was 16%, and the percentage of returns that were below -17 percent was approximately 52.3%.
To know more about portfolio visit:
brainly.com/question/31013505
#SPJ11
Solve the equation below
(2×-9)(×+8)
Answers
Answer:
-18x + -144
Step-by-step explanation:
Could someone please help me?

Answers
\(\textit{area of the rectangle}\\\\ A=Lw \begin{cases} L=length\\ w=width\\[-0.5em] \hrulefill\\ L=5\\ w=6 \end{cases}\implies A=(5)(6)\qquad \begin{cases} \textit{tripling the sides}\\[-0.5em] \hrulefill\\ L=3\cdot 5\\ w=3\cdot 6 \end{cases} \\\\\\ A=(3\cdot 5)(3\cdot 6)\implies (3\cdot 3)(5)(6)\implies 9(5)(6)\leftarrow \begin{array}{llll} \textit{new area is 9 times}\\ \textit{the old one}\\ \textit{a ratio of 9 : 1} \end{array}\)
i'll mark brainliest if it works so pls help me

Answers
Detirme the value of x
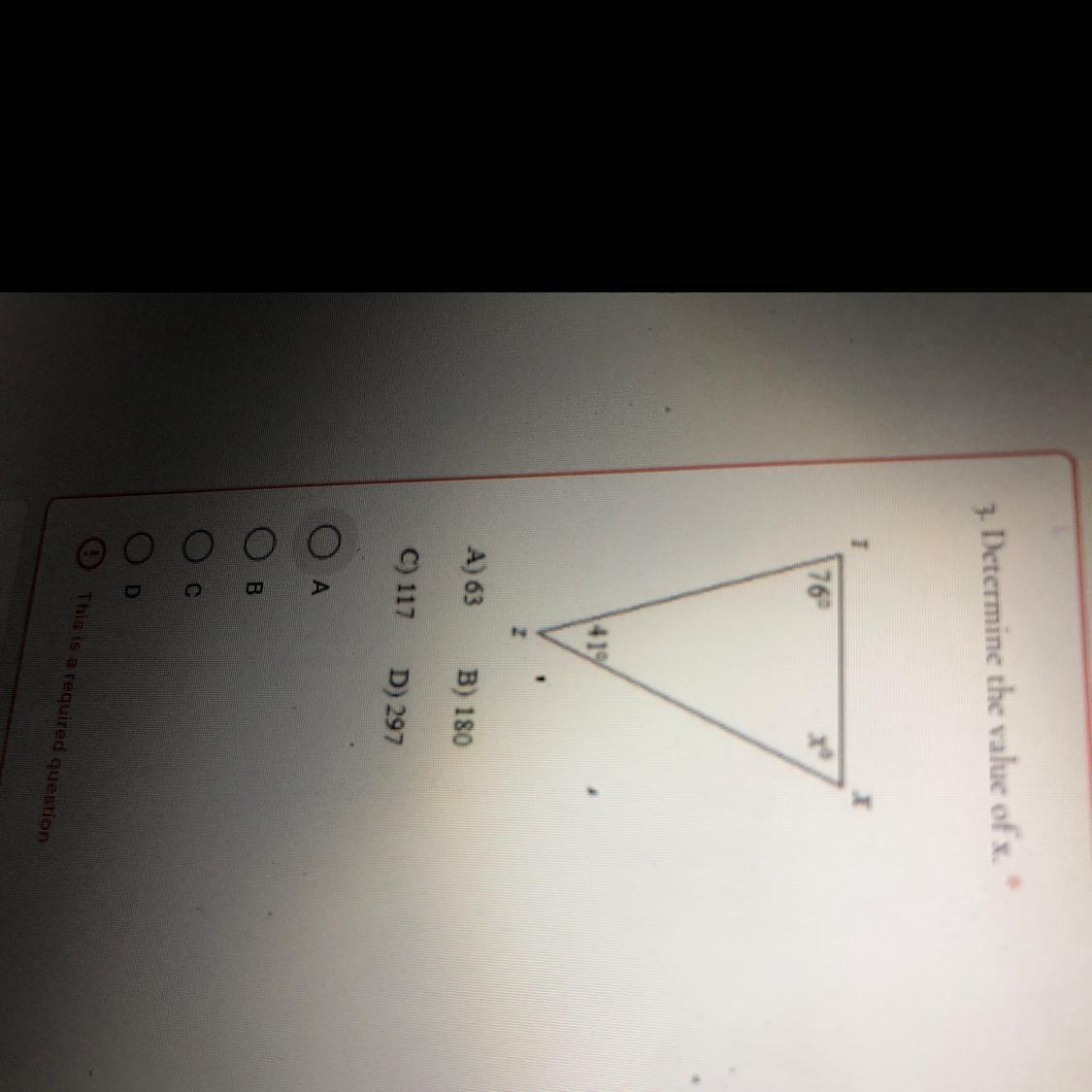
Answers
The total value of a triangle's angles is 180*
so x=180-y-z
x=180-76-41
x=63*
hope it helps
Matthew recorded the grade-level and instrument of everyone in the middle school School of Rock below. Seventh Grade Students Instrument# of Students Guitar13 Bass11 Drums5 Keyboard3 Eighth Grade Students Instrument# of Students Guitar9 Bass14 Drums8 Keyboard8 Based on these results, express the probability that a student chosen at random will play the keyboard as a decimal to the nearest hundredth.
Answers
Using it's concept, it is found that the probability that a student chosen at random will play the keyboard is of 0.15.
What is a probability?A probability is given by the number of desired outcomes divided by the number of total outcomes.
In this problem:
There is a total of 13 + 11 + 5 + 3 + 9 + 14 + 8 + 8 = 71 students.Of those, 11 play the keyboard.Hence:
\(p = \frac{11}{71} = 0.15\)
The probability that a student chosen at random will play the keyboard is of 0.15.
You can learn more about the probability concept at https://brainly.com/question/15536019