Answers
Answer:
Follow the steps I did in the explanation.
Step-by-step explanation:
It says to evaluate the equation :-
3.2 = 4/5(b - 5)
3.2 = (4/5 × b) + (4/5 × -5)
3.2 = 4/5b - 4
3.2 + 4 = 4/5b
5/4 × 7.2 = b
9 = b
Hope this helps, thank you :) !!
3.2 = 4/5(b - 5)
3.2 = (4/5 × b) + (4/5 × -5)
3.2 = 4/5b - 4
3.2 + 4 = 4/5b
5/4 × 7.2 = b
9 = b
Related Questions
Evaluate. 32−[(4+2×3)×2] Enter your answer in the box.
will give brainliest!!!!!
Answers
Find a and b using the factor theorem.
\(f(x)=x^3+ax^2+bx-12\) has factor \((x-1), (x+1)\)
Answers
The values of a and b using the factor theorem for the polynomial f(x), we set f(1) and f(-1) equal to zero. Solving the resulting system of equations, we find that a = 12 and b = -1.
To find the values of a and b using the factor theorem, we need to use the given factors (x - 1) and (x + 1) and the fact that they are roots of the polynomial f(x).
The factor theorem states that if (x - c) is a factor of a polynomial, then f(c) = 0. Therefore, we can set x = 1 and x = -1 in the polynomial f(x) to get two equations.
First, let's substitute x = 1 into f(x):
f(1) = (1)^3 + a(1)^2 + b(1) - 12
f(1) = 1 + a + b - 12
Next, let's substitute x = -1 into f(x):
f(-1) = (-1)^3 + a(-1)^2 + b(-1) - 12
f(-1) = -1 + a - b - 12
Since (x - 1) and (x + 1) are factors, f(1) and f(-1) must equal zero. Therefore, we can set the two equations equal to zero and solve for a and b:
1 + a + b - 12 = 0
-1 + a - b - 12 = 0
Rearraning the equations, we have:
a + b = 11
a - b = 13
Now, we can solve this system of equations. Adding the two equations, we get:
2a = 24
a = 12
Substituting the value of a into one of the equations, we find:
12 - b = 13
b = -1
Therefore, the values of a and b are 12 and -1 respectively.
For more such questions on polynomial
https://brainly.com/question/1496352
#SPJ8
solve the PDE using separation of variables method Uxx = 1/2 Ut 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Answers
The general solution of the partial differential equation is:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
How to solve Partial Differential Equations?The partial differential equation (PDE) is given as:
Uxx = (1/2)Ut with the boundary and initial conditions as 0< X <3 with U(0,t) = U(3, t)=0, U(0, t) = 5sin(4πx)
Assume that the solution can be written as a product of two functions:
U(x, t) = X(x)T(t)
Substituting this into the PDE, we have:
X''(x)T(t) = (1/2)X(x)T'(t)
Dividing both sides by X(x)T(t), we get:
(X''(x))/X(x) = (1/2)(T'(t))/T(t)
Since the left side only depends on x and the right side only depends on t, both sides must be equal to a constant, denoted as -λ²:
(X''(x))/X(x) = -λ²
(1/2)(T'(t))/T(t) = -λ²
Simplifying the second equation, we have:
T'(t)/T(t) = -2λ²
Solving the second equation, we find:
T(t) = Ce^(-2λ²t)
Applying the boundary condition U(0, t) = 0, we have:
U(0, t) = X(0)T(t) = 0
Since T(t) ≠ 0, we must have X(0) = 0.
Applying the boundary condition U(3, t) = 0, we have:
U(3, t) = X(3)T(t) = 0
Again, since T(t) ≠ 0, we must have X(3) = 0.
Therefore, we can conclude that X(x) must satisfy the following boundary value problem:
X''(x)/X(x) = -λ²
X(0) = 0
X(3) = 0
The general solution to this ordinary differential equation is given by:
X(x) = Asin(λx) + Bcos(λx)
Applying the initial condition U(x, 0) = 5*sin(4πx), we have:
U(x, 0) = X(x)T(0) = X(x)C
Comparing this with the given initial condition, we can conclude that T(0) = C = 5.
Therefore, the complete solution for U(x, t) is given by:
U(x, t) = Σ [Aₙsin(λₙx) + Bₙcos(λₙx)]*e^(-2(λₙ)²t)
where:
Σ represents the summation over all values of n
λₙ are the eigenvalues obtained from solving the boundary value problem for X(x).
To find the eigenvalues λₙ, we substitute the boundary conditions into the general solution for X(x):
X(0) = 0: Aₙsin(0) + Bₙcos(0) = 0
X(3) = 0: Aₙsin(3λₙ) + Bₙcos(3λₙ) = 0
From the first equation, we have Bₙ = 0.
From the second equation, we have Aₙ*sin(3λₙ) = 0. Since Aₙ ≠ 0, we must have sin(3λₙ) = 0.
This implies that 3λₙ = nπ, where n is an integer.
Therefore, λₙ = (nπ)/3.
Substituting the eigenvalues into the general solution, we have:
U(x, t) = Σ [Aₙ*sin((nπ/3)x)]*e^(-(nπ/3)²t)
where Aₙ are the coefficients that can be determined from the initial condition.
Read more about Partial Differential Equations at: https://brainly.com/question/28099315
#SPJ1
Cassie has a small cube-shaped box. Its volume is 64 cubic centimeters.
What is the area of one face of the box? Enter your answer in the box.
PLZ HELP DUE IN 5 MINUTES
Answers
Answer: one face is 16 square inches
Step-by-step explanation:
\(\sqrt[3]{64} = 4\) side length
4 × 4 = 16 the area of one face
What is the quotient of 3/4 divided by 1/5 the quotient is 3 and
Answers
Answer:
3 3/4
Step-by-step explanation:
\(\dfrac{\left(\dfrac{3}{4}\right)}{\left(\dfrac{1}{5}\right)}=\dfrac{3}{4}\cdot\dfrac{5}{1}=\dfrac{15}{4}\\\\=\dfrac{12}{4}+\dfrac{3}{4}=\boxed{3\frac{3}{4}}\)
Answer:
3 3/4
Step-by-step explanation:) :) :)
Olivia measures the heights of two trees and the lengths of their shadows. She notices that the height of each tree and the length of its shadow are directly proportional. One of the trees has a height of 15 m and a 10 m long shadow. The other tree has a 14.4 m long shadow. Calculate its height, in metres (m). Give any decimal answers to 1 d.p. 15 m 10 m ? m 14.4 m
Answers
Step-by-step explanation:
directly proportional means
y = kx
with k being a constant factor for all values of x.
we get k by using the given data point (10, 15).
15 = k×10
k = 15/10 = 1.5
so, now for the other tree we know k and x and calculate y
y = 1.5×14.4 = 21.6 m
it is 21.6 m tall (its height is 21.6 m).
There are 80 questions on a test. 1/4 of the answers are the letter A, 20% of the answers are letter B, 28 answers are the letter C, How many answers are the letter D?
18
28
20
16
Answers
Answer:
16
Step-by-step explanation:
1/4 is 20
20per is 16
20+16+28 is 64 minus 80 is 16
Financial reporting issues that result from foreign direct investment are (a) conversion of foreign GAAP to parent company GAAP and (b) translation of foreign currency to parent company reporting currency to prepare consolidated financial statements. In addition, supplementary disclosures about foreign operations might be required.
Answers
Answer:b
Step-by-step explanation: didn 9t
What is the discounted price for a watch that is regularly $58.00 and 30% off?
Answers
Answer:
$40.60
Step-by-step explanation:
Camacho is buying a monster truck. The price of the truck is xxx dollars, and he also has to pay a 13\%13%13, percent monster truck tax. How much does Aubrey tip the waitstaff?
Answers
Answer:We will consider the price of the truck to be $x
And the amount of tax in the percentage would be 13%
13/100
= $ 0.13x (this is the actual amount of the tax)
Now we will calculate the total price of the truck =
$x + $ 0.13x
= $ x(1 + 0.13)
Step-by-step explanation:
If numbers collected from a survey are measurements, what are these measurements called before you perform any calculations?
Answers
Answer: raw data
Step-by-step explanation:
Raw data, is also referred to as the primary data, and it refers to the data that's collected from a source. It is a day that is yet to be processed. e.g the raw scores during examination can be considered to be raw data since it hasn't been processed yet to get further information.
Therefore, if the numbers collected from a survey are measurements, then the measurements before any calculation is performed is called raw data.
Let U = {English, French, History, Math, Physics, Chemistry, Psychology, Drama}, A = {Chemistry, Psychology, Math, History}, B = {Drama, English, French, Math, History}, and C = {Physics, Psychology, French}. Find the following. n(B ∪ C)
Answers
Drama, English, French, Math, History, Physics, Psychology
(08.03|08.04 HC)
For the regions A and B shown in the graph:
Part A: Discuss the limits of integration. (3 points)
Part B: Set up an integral expression that represents the total area. (4 points)
Part C: Calculate the total area. (3 points)

Answers
The total area from the graph is 2.737.
What is area?Area is the amount of space occupied by a two-dimensional figure. In other words, it is the quantity that measures the number of unit squares that cover the surface of a closed figure. The standard unit of area is square units which is generally represented as square inches, square feet, etc.
First of all, lets calculate the points of intersection (P, Q, R)
x²+3=(x+2) +5
x²-2=√(x+2)
x⁴+4-4x²=x+2
x⁴-4x²-x+2=0
(x-2)(x³+2x²-1)=0
(x-2)(x+1)(x²+x-1)=0
x=2, -1, -1±√(1+4)/2
Clearly, the x-coordinate of Q is -1, P is -1-√5/2, R is -1+√5/2, S is 2
So the limit of integration will be
P( (-1-√5)/2, (-1-√5/2)² +3)=P((-1-√5)/2, (3+√5/2))
Q(-1, (-1)²+3)=Q(-1, 4)
Area A:
\(\int\limits^\frac{3+\sqrt{5} }{2} _4 {-\sqrt{-y-3}-((y-5)^2 -2)} \, dx\)
= \([\frac{-(y-3)^\frac{3}{2} }{\frac{3}{2} }-\frac{(y-5)^3}{3}+3y]^{\frac{3+\sqrt{5} }{2} }_4\)
= 2.07
Area B:
\(\int\limits^\frac{-1+\sqrt{5} }{2} _4 {-\sqrt{x+2}+5-(x^2+3)} \, dx\)
= \([\frac{-(x+2)^\frac{3}{2} }{\frac{3}{2} }+5x-\frac{x^3}{3}-3x]^{\frac{-1+\sqrt{5} }{2} }_{-1}\)
= 0.667
Total area = 2.07+0.667
= 2.737
Therefore, the total area from the graph is 2.737.
Learn more about the area here:
https://brainly.com/question/27683633.
#SPJ1
Find the area and perimeter of the figure
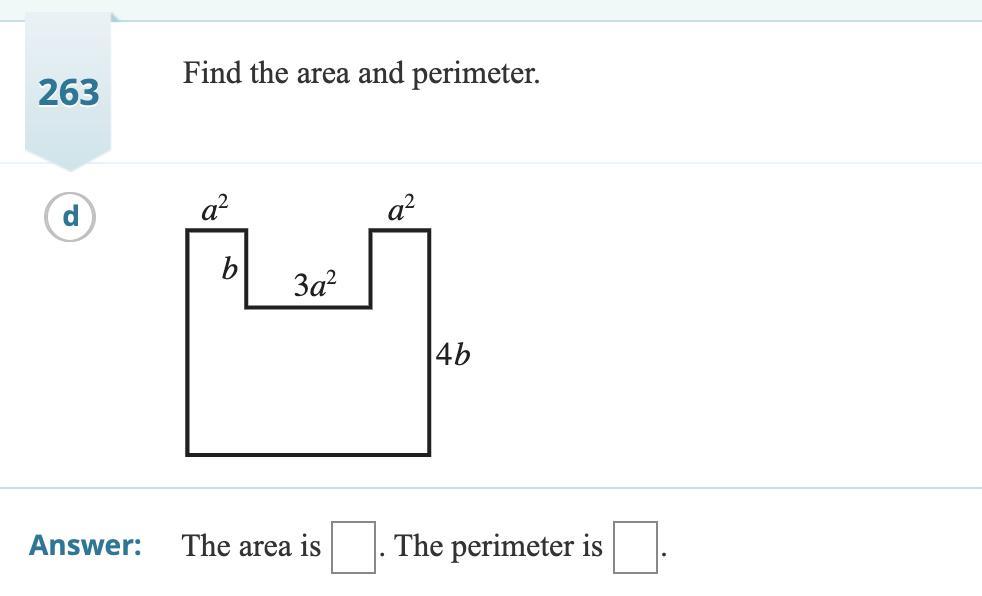
Answers
The perimeter and area of the given composite shape are respectively; 10a² + 10b and 37a²b
How to find the area and perimeter of a composite figure?The perimeter of the composite figure here will simply be the sum of the entire boundary lengths and as such we have;'
Perimeter = 2(a² + 3a² + a²) + 2(4b) + b + b
= 10a² + 8b + 2b
= 10a² + 10b
The area of a rectangle is;
Area = Length * width.
Thus;
Area of composite shape = Overall area of rectangle - Area of cut out rectangle
Area = (10a² * 4b) - (3a² * b)
Area = 40a²b - 3a²b
Area = 37a²b
Read more about composite figure perimeter and area at; https://brainly.com/question/28838199
#SPJ1
HEY EVERY ITS ME EVERYBODY'S FAVORITE [[number 1 rated salesman 1997]]
SPAMTON G SPAMTON
anyways here have some fre [[pipis]]
Answers
Answer:
ok
Step-by-step explanation:
thanks for the points also i will download the file
Answer:
omg spamton and his world famous pipis
Step-by-step explanation:
<3
select the statements and number line that can represent the inequality.

Answers
Answer:
every equivalent to 6 ≤ x
Step-by-step explanation:
We can subtract 5+11/6x to get ...
7 ≤ -(11/6)x +3x = (7/6)x
Multiplying by 6/7 gives ...
6 ≤ x
__
When x is in the set of real numbers, x in any real number that is 6 or more.
When x is in the set of integers, x is any integer that is 6 or more: {6, 7, 8, ...}.
When no set is specified, the solution is simply ...
6 ≤ x

During the year 2011 season a quarterback passed for 302 yd per game he played on my 16 regular season game for that year for how many total yards did the quarterback pass
Answers
Answer:
4,832 yards
Step-by-step explanation:
302x16=
classify each polygon by its number of sides then label it as convex or concave.

Answers
Hexagon - concave, Quadrilateral - Convex, Decagon - concave, Dodecagon - concave.
What is polygon?
A polygon is a 2-dimensional closed shape made up of straight line segments. It is a flat shape with three or more straight sides and angles.
A polygon is a closed plane figure with straight sides, defined by three or more line segments that meet at points called vertices. The sides of a polygon do not cross each other, and the angles between adjacent sides are called interior angles.
The classification of polygons is based on the number of sides they have. For example, a polygon with three sides is called a triangle, a polygon with four sides is called a quadrilateral, and so on.
Polygons can also be classified as either convex or concave. A convex polygon has all its interior angles less than 180 degrees, meaning that all its corners point outwards. In contrast, a concave polygon has one or more interior angles greater than 180 degrees, which means that at least one of its corners points inwards.
The classification of a polygon by its number of sides and whether it is convex or concave can help us to identify and describe its properties and characteristics.
To learn more about polygon visit:
https://brainly.com/question/26583264
#SPJ1
A rectangular box has a volume of 15 cubic feet. The length, width, and height of the box are each doubled.
What is the new volume of the rectangular box?
O A. 30 cubic feet
OB. 60 cubic feet
O c. 90 cubic feet
OD. 120 cubic feet
Answers
Answer:
I BELIEVE the answer would be 30
The curve given by x = sin(t) and y = sin(t + sin(t)) has two tangent lines at the point (x,y) = (0,0). List both of them in order of increasing slope. Your answers should be in the form of y = f(x) without t's.
Line with smaller slope: y(x):
Line with larger slope: y(x):
Answers
Answer:
slope of the tangent
\(\frac{d y}{d x} = \frac{cos(x+sin^{-1}(x) (1+\sqrt{1-x^{2}) } }{\sqrt{1-x^{2} } }\)
The function y = f(x)
y(x) = 2 x + C
Step-by-step explanation:
Step(i):-
Given x= sin t ...(i)
Differentiating equation (i) with respective to 'x' , we get
\(\frac{d x}{d t} = cost\)
Given y = sin ( t + sin (t)) ...(ii)
Differentiating equation (ii) with respective to 'x' , we get
\(\frac{d y}{d t} = cos (t + sin t ) (1 + cos t)\)
Step(ii):-
\(\frac{dy}{dx} = \frac{\frac{dy}{dt} }{\frac{dx}{dt} }\)
\(\frac{d y}{d x} = \frac{cos(t+sin t) (1+cost)}{cost}\)
we know that
x = sin t
t = sin⁻¹ (x)
cost = √1 - sin²(t) = (√1-x²)
\(\frac{d y}{d x} = \frac{cos(x+sin^{-1}(x) (1+\sqrt{1-x^{2}) } }{\sqrt{1-x^{2} } }\)
\(\frac{d y}{d x} = \frac{cos(x+sin^{-1}(x) (1+\sqrt{1-x^{2}) } }{\sqrt{1-x^{2} } }\)
Put x =0 and y=0
\(\frac{d y}{d x} = 2\)
d y = 2 d x
Integrating with respective to 'x' , we get
y(x) = 2 x + C
Above are two different models of the same rectangular hallway. If the length of the model on the top is 6 cm, what is the length of the model on the bottom?
Answers
Answer: 15cm
Step-by-step explanation: If the length of the model on the top is 6 cm, then the length of the model on the bottom must be 15 cm
What are the 5 properties of rhombus and rectangle?
Answers
1. Opposite angles are equal in measure.
and
2. Diagonals bisect each other.
3. Any two adjacent angles add up to 180 degrees.
Properties of rhombus:
1. All sides are equal in length.
2. Opposite angles are equal.
3. Diagonals bisect each other at 90°.
4. Diagonals are respective angle bisectors.
5. Any two adjacent angles add up to 180 degrees.
6. The area of the rhombus is a product of the lengths of the 2 diagonals divided by 2.
Properties of rectangle:
1. Opposite sides are equal in length.
2. All the angles are 90°.
3. Diagonals bisect each other.
4. Any two adjacent angles add up to 180 degrees.
Hence, the common properties are
1. Opposite angles are equal in measure.
and
2. Diagonals bisect each other.
3. Any two adjacent angles add up to 180 degrees.
Learn more about rohmbus and rectangle here ;
https://brainly.com/question/96855
#SPJ4
Triangle X Y Z is shown. Angle X Y Z is 51 degrees and angle Y Z X is 76 degrees. The length of X Z is 2.6, the length of X Y is z, and Y Z is x. Law of sines: StartFraction sine (uppercase A) Over a EndFraction = StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction Which equation is correct and can be used to solve for the value of z? StartFraction sine (51 degrees) Over 2.6 EndFraction = StartFraction sine (76 degrees) Over z EndFraction StartFraction sine (51 degrees) Over 2.6 EndFraction = StartFraction sine (53 degrees) Over z EndFraction StartFraction sine (76 degrees) Over 2.6 EndFraction = StartFraction sine (51 degrees) Over z EndFraction StartFraction sine (76 degrees) Over 2.6 EndFraction = StartFraction sine (53 degrees) Over z EndFraction
ITS A

Answers
Using the law of sines, equation A). \(\frac{sin(51)}{2.6} = \frac{sin(76)}{z}\) is correct and can be used to solve for the value of z.
What is law of sines?The law of sine or the sine law states that the ratio of the side length of a triangle to the sine of the opposite angle, which is the same for all three sides. It is also known as the sine rule.
\(\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}\)
Similarly, In triangle XYZ,
\(\frac{sin(51)}{2.6} = \frac{sin(76)}{z}=\frac{sin(53)}{x}\)
Learn more about law of sines here
https://brainly.com/question/17289163
#SPJ2
At the start of a month, Sasha and Natalia each have a certain amount of money.
Sasha has $400 and saves $20 each week. The graph below shows the amount of money in Natalia's account each week
Whose monthly activity shows a greater rate of change, and by how much?
A) Sasha, by $10/week
B)Sasha, by $19/week
C) Natalia, by $10/week
D) Natalia, by $19/week

Answers
Answer:
Option (A)
Step-by-step explanation:
Sasha has an amount of $400 and saves $20 per week.
If we graph the savings of Sasha, her savings per week will be defined by the slope of the line = $20 per week
Similarly, from the graph attached,
Slope of the line given in the graph = Per week savings of Natalia
Slope of line passing through (0, 190) and (2, 210) will be,
Slope = \(\frac{y_2-y_1}{x_2-x_1}\)
= \(\frac{210-190}{2-0}\)
= 10
Therefore, per week savings of Natalia = $10
Difference in savings of Sasha and Natalia = 20 - 10 = $10 per week
Here, Sasha shows the greater rate of change by $10 per week
Therefore, Option (A) will be the answer.
Continuously Compounding: A(t)=A(0)x e^rt
3. The amount of a radioactive element in a compound decreases continuously at an hourly rate of 15%. At noon there are 4500 nanograms of the element in the compound. How much of the element will there be at 6 p.m.?
4. A population of seabirds has been growing continuously at a rate of 4% per year. Today, the population is 16,000.
a. What will the population be 6 years from now?
b.What was the population 6 years ago?
Answers
Therefore, the population of seabirds 6 years ago was approximately 11,745.5.
What is percent?Percent is a way of expressing a number as a fraction of 100. It is represented by the symbol "%". For example, if there are 25 students in a class and 20 of them passed the test, the percentage of students who passed the test is 80%. This is calculated by taking the number of students who passed (20) and dividing it by the total number of students (25), then multiplying by 100.
Here,
3. The amount of the radioactive element can be modeled by the equation:
\(A(t) = A(0) *e^{rt}\)
where A(t) is the amount of the element at time t, A(0) is the initial amount at time t=0, r is the continuous rate of decrease, and e is the mathematical constant approximately equal to 2.71828.
In this problem, we know that the initial amount A(0) is 4500 nanograms, the continuous rate of decrease r is 15% per hour, and we want to find the amount of the element at 6 p.m., which is 6 hours after noon.
First, we need to convert the continuous rate of decrease from hourly to continuous, using the formula:
r = ln(1 - p)
where p is the hourly rate of decrease, expressed as a decimal. In this case, p = 0.15, so:
r = ln(1 - 0.15)
≈ -0.1707
Substituting the given values into the equation for A(t), we get:
\(A(t) = 4500*e^{-0.1707t}\)
where t is the time in hours since noon. To find the amount of the element at 6 p.m. (t = 6), we plug in t = 6 and evaluate:
\(A(6) = 4500*e^{-0.1707*6}\)
≈ 2595.5
Therefore, there will be approximately 2595.5 nanograms of the element at 6 p.m.
4a. The population of seabirds can be modeled by the equation:
\(P(t) = P(0)*e^{rt}\)
where P(t) is the population at time t, P(0) is the initial population at time t=0, r is the continuous rate of growth, and e is the mathematical constant approximately equal to 2.71828.
In this problem, we know that the initial population P(0) is 16,000, the continuous rate of growth r is 4% per year, and we want to find the population 6 years from now.
We need to convert the continuous rate of growth from years to continuous, using the formula:
r = ln(1 + p)
where p is the annual rate of growth, expressed as a decimal. In this case, p = 0.04, so:
r = ln(1 + 0.04)
≈ 0.0392
Substituting the given values into the equation for P(t), we get:
\(P(t) = 16000*e^{0.0392t}\)
where t is the time in years since the initial time. To find the population 6 years from now (t = 6), we plug in t = 6 and evaluate:
\(P(6) = 16000*e^{0.0392*6}\)
≈ 20661.7
Therefore, the population of seabirds will be approximately 20,661.7 in 6 years.
4b. To find the population 6 years ago, we can use the same equation but with t = -6 (since we are going back in time):
\(P(6) = 16000*e^{0.0392*-6}\)
≈ 11745.5
To know more about percent,
https://brainly.com/question/29172752
#SPJ1
rotate the figure 90 degrees clockwise then translate 4 units left

Answers
Answer:
If I am not mistaken, the new figure will be here (view attachment, bright blue figure is the new transformation)

Answer:
For each of the following equations determine the output values Corresponding to the input value
(-2;-1;0;1;2;3)
What is the value of x in this proportion?

Answers
The value of x in this proposition would be the first option i.e. \(-13\frac{1}{4}\)
4/11= -33/x+5,
to get the value of x we need to get the x to the left hand side,
4(x+5)= -33,
4x+20 = -33.
subtracting 20 from both the sides,
4x= -33-20
4x = -53.
dividing both the sides by 4,
x= -53/4
x= \(-13\frac{1}{4}\) ,
which is option A in the given question
To know more about solving equations,
https://brainly.com/question/30106736
a, b, and c are positive real numbers;
a×b= 5742×6368
a×c= 5748×6362
c×b= 5738×6372
?<?<?
And please clarify your answers in a simple language
Answers
Given the equations a × b = 5742 × 6368, a × c = 5748 × 6362, and c × b = 5738 × 6372, we need to determine the relationship between the three variables a, b, and c.
By comparing the given equations, we notice that the numbers on the right-hand side of each equation are very close to each other, differing only by small amounts. This suggests that a, b, and c are approximately equal.Since a × b, a × c, and c × b involve the same numbers with slight variations, we can conclude that a, b, and c are all very close in value.
Therefore, the inequality we can infer from this information is a ≈ b ≈ c, indicating that a, b, and c are approximately equal.
In simple terms, based on the given equations, it suggests that the values of a, b, and c are very similar or approximately equal to each other.
For more such questions on equations
https://brainly.com/question/29174899
#SPJ8
Please answer! giving brainliest !

Answers
Answer:
x = 19
Step-by-step explanation:
you can set up a proportion among corresponding sides:
2x -14 = 18
32 24
18 /24 can be reduced to 3/4
2x - 14 = 3
32 4
cross-multiply: 4(2x - 14) = 32(3)
8x - 56 = 96
8x = 152
x = 19
An equation is shown below:
5(3x − 4) = 1
Which of the following correctly shows the first two steps to solve this equation?
A. Step 1: 8x + 1 = 1; Step 2: 8x = 0
B. Step 1: 15x − 4 = 1; Step 2: 15x = 5
C. Step 1: 8x − 9 = 1; Step 2: 8x = 10
D. Step 1: 15x − 20 = 1; Step 2: 15x = 21
Answers
Answer:
The answer is D
…………………………
