Use Fermat's little theorem to find 82035 mod 17
Answers
Using Fermat's little theorem, 82035 mod 17 is equal to 1. Fermat's Little Theorem states that when a prime number (denoted as p) divides an integer (denoted as a), the remainder obtained when a raised to the power of p-1 is divided by p will always be 1.
In simpler terms, it asserts that if a and p are numbers that meet specific conditions, then a to the power of p-1 will have a remainder of 1 when divided by p.
In this case, we have p = 17 and a = 82035.
Since 17 is a prime number and 82035 is not divisible by 17, we can apply Fermat's Little Theorem to find 82035 mod 17.
The theorem tells us that (82035)^(17-1) is congruent to 1 modulo 17.
Now, let's calculate the exponent:
17 - 1 = 16
Therefore, we have:
82035^16 ≡ 1 (mod 17)
To find 82035 mod 17, we can reduce the exponent to the remainder when divided by 16.
82035 mod 16 = 3
So, we have:
82035 ≡ 82035^1 ≡ 82035^16 ≡ 1 (mod 17)
Hence, 82035 mod 17 is equal to 1.
To learn more about theorem: https://brainly.com/question/343682
#SPJ11
Related Questions
Help look at the photo
Will mark the brainlest

Answers
Answer:
1. 6
2. 8
3. 10
4. 12
5. 14
Step-by-step explanation:
just solve
Please Help me - You will get 60 points for the rapid reply- Use isosceles trapezoid ABCD to determine the following measurements-

Answers
Answer:
1) AD = 9 in
2) DE = 9.25 in
3) ∠EDC = 36°
4) ∠AEB = 108°
5) 11.5 in
Step-by-step explanation:
1) AD = BC = 9in
2) AC = BD (diagonals are equal)
⇒ BD = 14.25
⇒ BE + DE = 14.25
⇒ 5 + DE = 14.25
DE = 9.25
3) Since AB ║CD,
∠ABE = ∠EDC = 36°
4) ∠ABE = ∠BAE = 36°
Also ∠ABE + ∠BAE + ∠AEB = 180 (traingle ABE)
⇒ 36 + 36 + ∠AEB = 180
∠AEB = 108
5) midsegment = (AB + CD)/2
= (8 + 15)/2
11.5
How many significant figures should be included in the answer to the following calculation? (3.4876)/(4.11+1.2
Answers
The calculation (3.4876)/(4.11+1.2) should be reported with three significant figures: 0.657.
To determine the number of significant figures in the answer to the calculation (3.4876)/(4.11+1.2), we need to consider the number of significant figures in the given values and apply the rules for significant figures in mathematical operations.
First, let's analyze the number of significant figures in the given values:
- 3.4876 has five significant figures.
- 4.11 has three significant figures.
- 1.2 has two significant figures.
To perform the calculation, we divide 3.4876 by the sum of 4.11 and 1.2. Let's evaluate the sum:
4.11 + 1.2 = 5.31
Now, we divide 3.4876 by 5.31:
3.4876 / 5.31 = 0.6567037...
Now, let's determine the number of significant figures in the result.
Since division and multiplication retain the least number of significant figures from the original values, the result should be reported with the same number of significant figures as the value with the fewest significant figures involved in the calculation.
In this case, the value with the fewest significant figures is 5.31, which has three significant figures.
Therefore, the answer to the calculation (3.4876)/(4.11+1.2) should be reported with three significant figures: 0.657.
To learn more about significant figures click here:
brainly.com/question/31437050
#SPJ11
Find the requested angle supplement of 123^%A/246B/33C/57D/237
Answers
Given: The angle
\(123^0\)To Determine: The supplement of the given angle
Solution
Please note that two angle are supplement if they are add up to 180⁰
So if the supplement is x. Therefore
\(\begin{gathered} x+123^0=180^0 \\ x=180^0-123^0 \\ x=57^0 \end{gathered}\)Hence, the supplement of 123⁰ is 57⁰, OPTION C
suppose x is an exponential random variable with pdf fx(x) = a exp (-ax) for x>0 where a =6.27 where b=1.78
Answers
One standard deviation away from the mean, and about 95% of the values of X will be between 0 and 0.504
However, assuming that the variable b is not relevant to the problem, we can proceed to find the expected value and variance of the given exponential random variable X.
The expected value (mean) of an exponential distribution with parameter a is equal to 1/a, and the variance is equal to 1/a^2. Therefore, for X ~ Exp(6.27), we have:
E(X) = 1/6.27 = 0.159
Var(X) = 1/(6.27^2) = 0.025
These values give us an idea of the typical or average value of X, as well as the spread or variability of the distribution.
For example, we can expect that about 63% of the values of X will be between 0 and 0.318 (one standard deviation away from the mean), and about 95% of the values will be between 0 and 0.504 (two standard deviations away from the mean).
It is worth noting that the exponential distribution is often used to model waiting times or durations between events that occur randomly and independently at a constant rate.
For instance, X could represent the time until a radioactive atom decays, or the time until a customer arrives at a store.
The parameter a determines the average rate of occurrence of these events, and the pdf fx(x) gives the probability density of X taking a certain value x.
To know more about matrix click here
brainly.com/question/30389982
#SPJ11
Which of the following characteristics does not apply to a theoretical normal distribution? A) It is never negative. B) It is bell-shaped. C) It is bimodal. D) The mean, median, and mode are equal.
Answers
The characteristic that does not apply to a theoretical normal distribution is C) It is bimodal.
The main answer is C. An explanation for this is that a normal distribution has a single peak at the mean, and as we move away from the mean in either direction, the frequency of occurrence decreases.
Therefore, a normal distribution can never have two distinct peaks, making it impossible for it to be bimodal. All other options are characteristics of a normal distribution. In conclusion, a theoretical normal distribution is never negative, bell-shaped, and has equal mean, median, and mode, but it is not bimodal.
To know more about distribution visit:
https://brainly.com/question/29664127
#SPJ11
Can someone solve this equation for me?
\(f(x)=(1-0.08)^{(\frac{1}{52})^{12t}\)
Answers
Answer:
$\frac{4\cdot\left(5^2\right)^5\left(-20\right)^3\left(-8\ right)^{-6}}{5^{-3}\cdot\:25^3\ ... 3(−8) −65 −3· 25 3(( −5) −2) −4 =−251024 ( Decimal : −0.0244140625) .
what is 1/2h + 2h + 3/2h - 1 simplified?
Answers
Answer:
4h-1
Step-by-step explanation:
subtracted it with a scientific calculator and that was the answer
If P(B)=0.3,P(A∣B)=0.5,P(B ′ )=0.7, and P(A∣B ′ )=0.8, find P(B∣A).
Answers
If P(B)=0.3, P(A|B)=0.5, P(B')=0.7and P(A|B')=0.8, then the value of the probability P(B|A)= 0.2113
To find the value of P(B|A), follow these steps:
The probability of B given A can be given by the product of the probability of A given B and the probability of B, divided by the total probability of B. So, the formula for P(B|A) = P(A|B) * P(B) / [P(A|B)*P(B)+P(A|B')*P(B')]. Substituting the values, we get P(B|A) = (0.5) (0.3) / [(0.5) (0.3) + (0.8) (0.7)] ⇒P(B|A) = 0.15 / [0.15 + 0.56] ⇒P(B|A) = 0.15 / 0.71 ⇒P(B|A) = 0.2113. Therefore, P(B|A) = 0.2113.Learn more about probability:
brainly.com/question/13604758
#SPJ11
Help pls! (4c+4)(2c-3)
Answers
Answer:
8c2 - 4c - 12
Step-by-step explanation:
Answer:
8c^2-4c-12
Step-by-step explanation
So you have to multiply 4c into 2c and -3 first and then 4 into 2c and -3.
(4c+4)(2c-3)
4c X 2c is 8c^2
(4c+4)(2c-3)
4c X -3 is -12c
So for the 4c multiplying in you would get 8c^2 and -12c, but we still have to multiply in the 4
4 X 2c is 8c
(4c+4)(2c-3)
4 X -3 is -12
So then we would get 8c^2-12c+8c-12, however we can still combine the -12c and the 8c. Combining those would get -4c. So the final answer is 8c^2-4c-12
Melanie got a new employer-paid job through the Jones recruitment Agency. The job pays $52,400 per year, and the agency fee is equal to 25% of 1 month’s pay. How much must Melanie’s employer pay the agency?
Answers
Answer:
Melanie's employer must pay the agency a sum of $1,091.67
Step-by-step explanation:
job = $52,400
agency fee = 25% of 1 month's pay
52,400 / 12 = $4,366.67
.25 x $4,366.67 = $1,091.67
A scanner scanned 72 photos in 8 minutes. If it scans photos at a constant rate, it can scan ____ photos in 23 minutes.
What do I put in the blank?
Answers
Answer:
207
Step-by-step explanation:
ok so 72 photos in 8 minutes
So the easiest way would be to find how many photos are made per minute.
To do that you would divide 72 by 8 to get 9.
You need how many photos are made in 23 minutes.
To get that you times 23 by 9 to get 207.
207 photos are made in 23 minutes.
help, please
Given the triangle shown on the grid below, which graph shows the triangle reflected over the x-axis?

Answers
Step-by-step explanation:
Answer attached.
Hope it helps :)

2x - 8 = 7 + 5x
Solve for x
Answers
Answer:
-5
Step-by-step explanation:
2x-8=7-5x
collect like terms
2x-5x=7+8
-3x=15
x=15/-3
x=-5
Answer: The value of x is -5.
Step-by-step explanation:
As we know that LHS = RHS,
By bringing the constants to one side and variables to one side,the question can be solved.
Given in the question
2x-8 = 7+5x
on bringing variables to LHS,
2x-5x = 8+7
-3x = 15
x=(-15)/3 = -5
Hence the value of x is -5.
Use the Laplace transform to solve the initial-value problem x" + 4 = f(t), x(0)=0, x'(0) = 0, if t < 5 f(t) = t25. 3 sin(t-5) if t > 5.
Answers
By applying the initial conditions and inverse Laplace transforming, we can obtain the solution x(t) = (1 - cos(2t))u(t-5) + (3 sin(t-5))u(t-5), where u(t) is the unit step function. Therefore, the solution to the initial-value problem is x(t) = (1 - cos(2t))u(t-5) + (3 sin(t-5))u(t-5)
Taking the Laplace transform of the given differential equation x" + 4 = f(t), we obtain the algebraic equation in the Laplace domain: s^2X(s) + 4sX(s) + 4 = F(s), where X(s) is the Laplace transform of x(t) and F(s) is the Laplace transform of f(t).
Next, applying the initial conditions x(0) = 0 and x'(0) = 0, we get X(0) = 0 and sX(0) = 0. Substituting these initial conditions into the Laplace domain equation, we have s^2X(s) + 4sX(s) + 4 = F(s), with X(0) = 0 and sX(0) = 0.
Now, let's consider the Laplace transform of f(t) using the given piecewise function. For \(t < 5, f(t) = t^2/5, and for t > 5, f(t) = 3sin(t-5).\)Taking the Laplace transform of f(t) in each interval, we have \(F(s) = (1/s^3) + (3/s^2) for t < 5 and F(s) = (3/s^2) * (1/(s^2+1)) for t > 5.\)
Substituting these Laplace transforms into the equation\(s^2X(s) + 4sX(s) +\)4 = F(s), we can solve for X(s). Simplifying, we obtain \(X(s) = (1/s^3) + (3/s^2) / (s^2 + 4s + 4) + (3/s^2) * (1/(s^2+1)).\)
To find the inverse Laplace transform of X(s), we can split it into partial fractions and apply the inverse Laplace transform formula. The solution is x(t) = (1 - cos(2t))u(t-5) + (3 sin(t-5))u(t-5), where u(t) is the unit step function.
Therefore, the solution to the initial-value problem is x(t) = (1 - cos(2t))u(t-5) + (3 sin(t-5))u(t-5), where u(t) is the unit step function that ensures the piecewise function is activated at t = 5.
Learn more about Laplace transform here:
https://brainly.com/question/31040475
#SPJ11
need this rn
solving system of linear equation in two variables. Show your COMPLETE SOLUTION
1) 4x + 8y = 24 2) 2x + y = 19 3) 3x + y = 15
4x + 2y = 12 x + y = 11 x + 2y = 10
Answers
The solution to the system of equations is x = 4 and y = 2.
CalculationsWe would use the elimination method to solve the system of equations:
4x + 8y = 242x + y = 193x + y = 154x + 2y = 12x + y = 11x + 2y = 10Let's eliminate the variable y by adding equations 1 and 2:
4x + 8y = 24
2x + y = 19
.
.
.,
6x + 9y = 43
Now we can eliminate the variable x by subtracting equation 3 from the above equation:
6x + 9y = 43
3x + y = 15
.
.
.
3x + 8y = 28
We now have an equation with one variable: 3x + 8y = 28. We can solve for x by dividing both sides by 3:
x = (28 - 8y) / 3
Now we can substitute this expression for x into one of the original equations and solve for y. Let's use equation 4:
4x + 2y = 12
Substituting x = (28 - 8y) / 3:
4((28 - 8y) / 3) + 2y = 12
If we simplify:
28 - 8y + 2y = 128y = 16y = 2Finally, we can use this value of y to find x by plugging it into the expression we found earlier:
x = (28 - 8(2)) / 3
x = (28 - 16) / 3
x = 12 / 3
x = 4.
Read more about elimination method here:
https://brainly.com/question/25427192
#SPJ1
Solve for x. Options are 6,3,5,4.
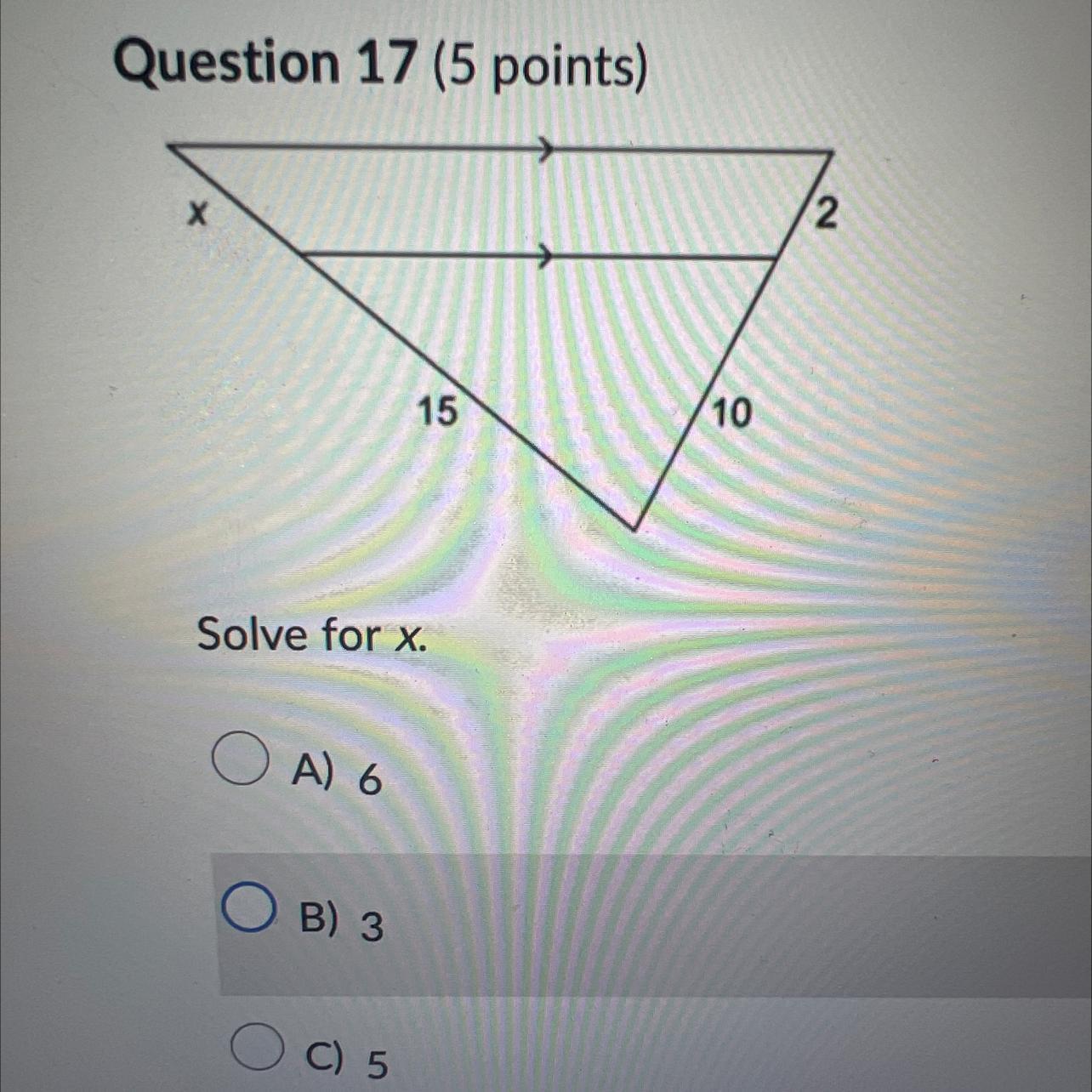
Answers
The value of x as required to be determined in the given task content is; 3.
What is the value of x in the given diagram?It follows from the task content that the value of x is required to be determined in the given task content.
By observation; the triangles formed by the parallel lines and the common vertex they share are similar triangles.
On this note, the ratio of their corresponding sides are equal and hence; we have that;
15 / (15 + x) = 10 / (10 + 2)
(15 × 12) = 10 (15 + x)
180 - 150 = 10x
30 = 10x
x = 3.
Consequently, it follows that the value of x as required is; 3.
Read more on similar triangles ratio;
https://brainly.com/question/31529028
#SPJ1
Which number is rational?

Answers
Answer:
\(5.3333333...\)
Step-by-step explanation:
\(5.\overline3 = \dfrac{53-5}{9} = \dfrac{48}9\)
The elevations, in feet, of three citites are marked on the number line shown below. The point 0 on the number line represents sea level. Which statement is true?

Answers
Answer:
cityQ
Step-by-step explanation:
City Q is located at the sea level
The statement that should be true is
City P is above sea level and City Q is below sea level.
What is the number line?The word "number line" in mathematics refers to a straight line where a number should be positioned at similar intervals or segments along with its length.
Given:
The point 0 on the number line represents sea level.
As, It should be presented in a horizontal style and be infinitely in any direction.
As a result, option c should be the statement that is true. City Q is below sea level, but City P is above it.
Learn more about number line here:
brainly.com/question/24489361
#SPJ2
What is the area of the triangle?
48 in 2
28 in 2
96 in 2
24 in 2

Answers
Answer:
48 in^2
Step-by-step explanation:
To find the area of a triangle is (1/2)*base*height, so (1/2)*4in*24in = 2in*24in = 48 in^2.
Answer:
48 in2
Step-by-step explanation:
when finding area we use the equation A= 1/2bh
b meaning base and h meaning height
so for this we would use A= 1/2(24)(4)
multiply them both to get A=1/2(96)
and then take half of 96 to get 48
so the answer is 48in 2
Fill in the blanks below with the correct units. (a) A large horse weighs about 1 . (b) A bucket holds about 4 of water. (c) A piece of paper is about 8 wide.
Answers
Each sentence should be completed with the correct unit as follows:
A large horse weighs about 1 pound. A bucket holds about 4 liter of water. A piece of paper is about 8 inches wide.What is measurement?Measurement can be defined as an act or process through which the size, weight, magnitude, quantity, volume (capacity), dimensions, or distance traveled by a physical object or body is taken, especially for the purpose of an experiment.
In Mathematics, the correct unit of measurement for the weight of a physical body such as a large horse is either pound, grams, or kilograms. Additionally, the correct unit of measurement for the volume (capacity) of a physical object such as a bucket is either liter, gallon, cubic centimeter, or cubic meter.
Lastly, the correct unit of measurement for the size (width) of a physical object such as a piece of paper is either inches, feet, centimeter, or meter.
Read more on measurements here: https://brainly.com/question/24529628
#SPJ1
88% of what number is 20?
Answers
Answer:
22.73
Step-by-step explanation:
Answer:
2 3/11
Step-by-step explanation:
2*100 ÷ 88=2 3/11
PLS PLS PLS HELP ME!!!

Answers
Answer:
The third one x+49+28=180
Step-by-step explanation:
We can say that the angle between the 29° angle and the 49° angle is equal to x, since they are vertically opposite angles.
The sum of 28+49+x is equal to a supplement angle which is a straight line essentially
We can then say x+28+49=180
:)
If you want to calculate x,
x=180-28-49
x=103
If a car travels 33.6 miles in 0.75 hours, then what distance does the car cover in an hour?
Answers
Answer:
44.8 miles
Step-by-step explanation:
We can use ratios to solve
33.6 miles x miles
-------------- = --------------
.75 hours 1 hours
Using cross products
33.6 * 1 = .75x
Divide each side by .75
33.6 / .75 =x
44.8 miles
How do you know if triangles are congruent in SAS?
Answers
With the help of the figure we can say that triangles are congruent by SAS Rule
What is Congruence of Triangle?
Triangle congruence: Two triangles are said to be congruent if all three of their corresponding sides are equal and all three of their corresponding angles are equal in size. These triangles can be moved, rotated, flipped, and turned to look exactly the same.
Solution:
By SAS rule, two triangles are said to be congruent if any two sides and the angle included between the sides of one triangle are comparable to the corresponding two sides and the angle included between the sides of the second triangle.
In given figure, sides AB= PQ, BC=QR and angle between AB and BC equal to angle between PQ and QR i.e. ∠B = ∠Q. Hence, Δ ABC ≅ Δ PQR.
To learn more about Congruence of Triangles from the given link
https://brainly.com/question/2938476
#SPJ4

Least to greatest. 6.35, 2.5 , -3.27 ,-7.44,3.141594653
Answers
Answer:
-7.44 ,-3.27,2.5,3.14 blah,6.35
Which of these relations is a function?

Answers
What is the slope of the given curve at the specified point?
x = cos (y): y = - π/3 A) m = 2 √3/3 B) m = - √2/2 C) m = 3 √2/4
D) m = - √3/2
Answers
The correct answer is D) m = -√3/2. To find the slope of the given curve at the point (x, y), we need to take the derivative of the curve with respect to x and evaluate it at the given point.
The equation of the curve is x = cos(y), and we want to find the slope at the point (x, y) = (-π/3). Taking the derivative of x = cos(y) with respect to x, we get: dx/dy = -sin(y) * dy/dx. To find the slope at the point (-π/3), we substitute y = -π/3 into the derivative expression: dx/dy = -sin(-π/3) * dy/dx = -(-√3/2) * dy/dx = √3/2 * dy/dx.
Therefore, the slope of the curve at the point (-π/3) is √3/2. Hence, the correct answer is D) m = -√3/2.
To learn more about derivative click here: brainly.com/question/25324584
#SPJ11
i = prt ; p = $2,000, r = 3%, and t = 2 yr.
Evaluate the expression using the given values.
Please and Thank you
Answers
The interest amount is $120 when given principal amount $2000, rate of interest per year is 3% and time period is 2 years.
Given that,
p = $2,000, r = 3%, and t = 2 yr.
We have to find the i when i=prt.
Here,
i is interest amount.
p is principal amount.
r is rate of interest per year.
t is time period.
So,
Formula for finding interest amount is
i=prt
So,
i=2000(3/100)(2)
i=20×3×2
i=120
Therefore, The interest amount is $120 when given principal amount $2000, rate of interest per year is 3% and time period is 2 years.
To learn more about interest visit: https://brainly.com/question/19291527
#SPJ1
Estimate ΔyΔy using differentials.
y=cos(5x),=/30,x=0.055
(Give your answer to three decimal places.)
Answers
The estimated change in yy using differentials is -0.00679. This means that if xx is increased by 0.005, then yy is estimated to decrease by 0.00679. The differential of yy is dy=-5sin(5x)dxdy=−5sin(5x)dx. We are given that y=cos(5x)=π/30y=cos(5x)=π/30 and x=0.055x=0.055.
We want to estimate ΔyΔy, which is the change in yy when xx is increased by 0.005. We can use the differential to estimate ΔyΔy as follows:
Δy≈dy≈dy=-5sin(5x)dx
Plugging in the values of y, x, and dxdx, we get:
Δy≈-5sin(5(0.055))(0.005)≈-0.00679
Therefore, the estimated change in yy using differentials is -0.00679.
To learn more about differential click here : brainly.com/question/31383100
#SPJ11