Use any direct or indirect method [on your choice] to prove the following statement:
For all positive real numbers r and s, \(\sqrt{r+s} \neq \sqrt{r}+\sqrt{s}\)
Answers
We have proven that (r + s)² ≥ 4rs for all positive real numbers r and s.
What are real numbers?
Real numbers are a set of numbers that includes all the rational and irrational numbers. They are called "real" numbers because they represent quantities that can be measured on a number line.
The statement to be proven is:
For all positive real numbers r and s,
(r + s)² ≥ 4rs
One possible way to prove this statement is through a direct proof.
Direct Proof:
Let r and s be positive real numbers. We want to show that (r + s)² ≥ 4rs.
Expanding the left-hand side, we have:
(r + s)² = r² + 2rs + s²
So, we need to show that:
r² + 2rs + s² ≥ 4rs
Subtracting 4rs from both sides, we get:
r² - 2rs + s² ≥ 0
The left-hand side can be written as the square of the difference of r and s:
(r - s)² ≥ 0
Since the square of any real number is non-negative, this inequality holds for all real numbers r and s.
Therefore, we have proven that (r + s)² ≥ 4rs for all positive real numbers r and s.
To learn more about real numbers from the given link:
https://brainly.com/question/551408
#SPJ1
Related Questions
A cone has a volume of 2560 Pi cm cubed and a height of 30cm. Find the radius
Answers
•A volume of 2560 pi cm cube
•A height of 30 centimeters
The the required one
•The radius of the cone
Then find the solution
Using the formula
V=πr squared * h/3
Solving for
r=3V 3·2560
π·30≈9.02703
πh=
if someone does this I'll give you 5 stars and follow you!

Answers
Answer:
The picture is really blurry, i can't see the questions
Warehouse Club Membership If the annual fee for a warehouse club membership is $100 and the reward rate is 2% on club purchases for the year, then the linear equation y = 100 - 0.02x models the actual annual cost of the membership y, in dollars. Here x represents the annual amount of club purchases, also in dollars. (a) Determine the actual annual cost of the membership if club purchases for the year are $2400 (b) What amount of club purchases would reduce the actual annual cost of the mem bership to $50? ) How much would a member have to spend in annual club purchases to reduce the annual membership cost to $0?
Answers
Answer:
(a) $52
(b) $2500
(c) $5000
Step-by-step explanation:
(a) y = 100 - 0.02x
x = 2400
y = 100 - 0.02(2400)
y = 100 - 48
y = 52
$52
(b) 50 = 100 - 0.02x
-50 = -0.02x
x = 2500
$2500
(c) 0 = 100 - 0.02x
0.02x = 100
x = 5000
$5000
Can you help me? I will give the brain crown.
Step by step would be preferred thank youuu!!
In AIJK, IJ || LM. Given that KI = 18, KL=8, and LM = 20, find IJ.
K
W
IJ =

Answers
Answer:
the length of IJ is 7.2 units.
Step-by-step explanation:
Since IJ is parallel to LM, we can use the property of similar triangles to solve for IJ.
Triangles KIJ and KLM are similar, so we have:
IJ/KL = KI/LM
Substituting the given values, we get:
IJ/8 = 18/20
IJ/8 = 9/10
Multiplying both sides by 8, we get:
IJ = (8)(9/10)
IJ = 7.2
Therefore, the length of IJ is 7.2 units.
Which story represents the equation six-sevenths times one-fourth?
A: Victoria drinks six-sevenths of a cup of milk. She drinks one-fourth of a cup more milk. How much milk did she drink in all?
B: Mike walked one-fourth mile and then he took the bus for six-sevenths miles to school. How many miles did he travel in total?
C: Victoria has six-sevenths of a pizza. She ate one-fourth of it for dinner. How much pizza did Victoria eat for dinner?
D: Mike has six-sevenths of a pie. He gives one-fourth to his brother. How much pie does he have left?
Answers
Answer:
C I think.
Step-by-step explanation:
I don't know for sure, but A, B and D all talk about adding or subtracting the answers together, while C tells us to find the fraction of a fraction so I'm pretty sure you multiply. Hope this helps!
A randomly generated list of integers from 1 to 5 is being used to simulate an event, with the numbers 1, 2, and 3 representing a success. what is the estimated probability of a success?
Answers
The estimated probability of a success is 3/5 or 0.6
How to determine the probabilityFrom the question, we have the following parameters that can be used in our computation:
Integers = 5
Success = 3
The probability of success is then calculated as
Probability = Success/Integrs
Substitute the known values in the above equation, so, we have the following representation
probability = 3/5 = 0.6
Read moree about probability at
https://brainly.com/question/24756209
#SPJ1
Someone help me with this math problem.

Answers
From the graph, she walked at a rate of \(\frac{25-10}{5-2}=5 \text{ ft/s}\).
Therefore, she walked faster on her next three walks compared to her first two walks.
I need help with this math problem

Answers
Step-by-step explanation:
given,
\( log_{7}(4) = 0.712 \\ log_{7}(12) = 1.277 \\ to \: find \: log_{7}( \frac{1}{3} ) \\ log_{7}( \frac{1}{3} ) = log_{7}( \frac{4}{12} ) \\ by \: logarithmic \: result \: log( \frac{a}{b} ) = log(a) - log(b) \\ implies \\ log_{7}( \frac{1}{3} ) \: = log_{7}(4) - log_{7}(12) \\ = 0.712 - 1.277 \\ = −0.565\)
I hope this is the answer.
pls mrk me brainliest, i rly worked hard on this i need to get the next rank
A line passes through the point (1,5) and has a slope of 7
Answers
Therefore, the equation of the line passing through the point (1,5) with a slope of 7 is y = 7x - 2.
The equation of a line in the point-slope form is given by the following equation:
y-y_1 = m(x-x_1)
where m is the slope of the line and (x1, y1) is any point on the line.
Therefore, we can write the equation of the line passing through the point (1,5) with a slope of 7 as follows:
y-5 = 7(x-1)
Expanding the right-hand side of the equation gives:
y-5 = 7x-7
Adding 5 to both sides of the equation gives:
y = 7x-2
For such more question on equation
https://brainly.com/question/29174899
#SPJ8
Are the ratios 1:4 and 6:10 equivalent?
Answers
Answer:
No
Step-by-step explanation:
For ratios to be equivalent, they need to have something in common like 2:4
4:8. Those are common because ":2:4" is the simplified version of 4:8. (I mean it could be simplified to 1:2 but this is used as an example) (mark brainliest plas)
How many coupons can be generated

Answers
The number of coupon codes that can be generated is given as follows:
247,808 coupon codes.
What is the Fundamental Counting Theorem?The Fundamental Counting Theorem states that if there are m ways to do one thing and n ways to do another, then there are m x n ways to do both.
This can be extended to more than two events, where the number of ways to do all the events is the product of the number of ways to do each individual event, according to the equation presented as follows:
\(N = n_1 \times n_2 \times \cdots \times n_n\)
The codes are composed as follows:
Two letters -> each with 22 options, as letters can be repeated.Three digits -> each with 8 options, as digits can also be repeated.Thus the total number of codes is obtained as follows:
N = 22² x 8³
N = 247,808 coupon codes.
More can be learned about the Fundamental Counting Theorem at https://brainly.com/question/15878751
#SPJ1
The following exchange rate is given: £1 = 1.33 dollars. Convert £8 into dollars.
Answers
If £1 = $1.33, £8 is $10.64.
What is a unit rate?It is the quantity of an amount of something at a rate of one of another quantity.
In 2 hours, a man can walk for 6 miles
In 1 hour, a man will walk for 3 miles.
We have,
£1 = $1.33
Multiply 8 on both sides.
£8 = 8 x $1.33
£8 = $10.64
Thus,
£8 is $10.64
Learn more about unit rates here:
https://brainly.com/question/11258929
#SPJ2
What is the range of f(x) = -62*?
O A. y< 1
OB. y<0
O C. y> 0
O D. All real numbers
Answers
Answer:
D. all real numbers
Step-by-step explanation:
i think this is the answer sorry if you get it wrong.
64 + (5 ÷ 3) - 2^3
help me plz
Answers
Answer:
57.67
Step-by-step explanation:
64+1.67-8
65.67-8
57.67
Sammy draws 3 identical rectangles on his paper. If each rectangle has a base of 15 cm and a height of 12 cm, what is the total area of all 3 rectangles added together?
Answers
Answer:
540
Step-by-step explanation:
If you do 15x12 which is the formula for area for a rectangle, you get 180. That's only the area of one rectangle but if you multiply it by 3 you get 540 for the areas added together.
Answer:
540 cm
Step-by-step explanation:
you multiply 15 x12 If you are getting an area 15 x12=180 then you multiply 180 by 3 180x3=540 I think
A scuba diver was at a depth of 125 feet below sea level. He descends 205 more feet below sea level. What is the new depth of the scuba diver?
Answers
Answer:
The new depth of the scuba diver is 330 feet below sea level.
Step-by-step explanation:
125 + 205 more below sea level = 330 below sea level
which is an equation for the line that passes through the origin and has a slope of\( \frac{3}{5} \)
Answers
We have the next information
slope = 3/5
passes in the origin in (0,0)
The equation of the line in slope - intercept form is
\(y=mx+b\)where m is the slope and b is the y-intercept
The y-intercept is the value of the coordinate y, when the coordinate x is 0 in, this case because the line passes through the origin the y-intercept is 0
The equation of the line is
\(\begin{gathered} y=\frac{3}{5}x+0 \\ y=\frac{3}{5}x \end{gathered}\)How many more dogs are there than
cats and snakes combined?
Answers
Answer:
need more info like how many snakes there our
Step-by-step explanation:
need more info sorry
simplify the expression

Answers
Answer:
\( \frac{2 |x| }{ \sqrt{3y} } \)
1)carla tiene 628 galletitas para preparar una torta, cada piso tendra 24 galletitas¿cuantos pisos puede armar?,¿le sobran galletitas o le alcanza justo?
POR FAVOR ES PARA HOY
Answers
Answer:
puede hacer 26 pisos y le sobran 4 galletas
help me pls i need this right now

Answers
Answer:
Step-by-step explanation:
Area = (3√3 s2)/
A≈259.81
Answer:
259.8
Step-by-step explanation:
259.81 rounded to the nearest tenth is 259.8
In the diagram below of triangle ABC, D is a midpoint of AB and E is a midpoint of BC. If DE =9x-20, and AC =5x+12, what is the measure of AC?
Answers
Applying the triangle midsegment theorem, the measure of AC is: 32 units.
How to Apply the Triangle Midsegment Theorem?Since DE is a midsegment of triangle ABC, the triangle midsegment theorem therefore states that the length of DE is half of the length of the third side of the triangle, AC.
Given the following:
DE = 9x - 20
AC = 5x + 12
Find the value of x by creating an equation to solve:
DE = 1/2(AC) [based on the triangle midsegment theorem]
Substitute:
9x - 20 = 1/2(5x + 12)
Solve for x:
2(9x - 20) = 5x + 12
18x - 40 = 5x + 12
18x - 5x = 40 + 12
13x = 52
Divide both sides by 13
13x/13 = 52/13 [division property of equality]
x = 4
AC = 5x + 12
Plug in the value of x
AC = 5(4) + 12
AC = 32 units.
Learn more about the triangle midsegment theorem on:
https://brainly.com/question/12234706
#SPJ1

Sample response: The product of two numbers with
different signs is negative, so 2(-12) = -24, not 24. Then
-24-(-30) = -24 + 30 = 6.
Select all the information you considered when writing
your response.
The product or quotient of two integers with
different signs is negative.
To subtract an integer, add its opposite.
To add integers with opposite signs, subtract the
absolute values. The sum has the same sign as the
integer with the greater absolute value.
Answers
By considering these rules and properties of integers, the correct result of 6 was obtained.
When writing the response, I considered the following information:
The product or quotient of two integers with different signs is negative. This rule was used to determine that 2(-12) equals -24, not 24.
To subtract an integer, add its opposite. This rule was applied when subtracting -30 from -24, resulting in -24 - (-30) = -24 + 30.
To add integers with opposite signs, subtract the absolute values. The sum has the same sign as the integer with the greater absolute value.
This rule was used to calculate -24 + 30 = 6, where the absolute value of 30 is greater than the absolute value of -24.
By considering these rules and properties of integers, the correct result of 6 was obtained.
for such more question on integers
https://brainly.com/question/22008756
#SPJ8
Many elementary school students in a school district currently have ear infections. A random sample of children in two different schools found that 16 of 40 at one school and 13 of 30 at the other had this infection. Conduct a test to answer if there is sufficient evidence to conclude that a difference exists between the proportion of students who have ear infections at one school and the other. Find the test statistic. [Suggestion: try to use a TI 83 or a similar calculator.]
Answers
Answer:
The test statistic is \(z = -0.28\)
Step-by-step explanation:
First, before finding the test statistic, we need to understand the central limit theorem and difference between normal variables.
Central Limit Theorem
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean \(\mu\) and standard deviation \(\sigma\), the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean \(\mu\) and standard deviation \(s = \frac{\sigma}{\sqrt{n}}\).
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean \(\mu = p\) and standard deviation \(s = \sqrt{\frac{p(1-p)}{n}}\)
Subtraction between normal variables:
When two normal variables are subtracted, the mean is the difference of the means, while the standard deviation is the square root of the sum of the variances.
A random sample of children in two different schools found that 16 of 40 at one school
This means that:
\(p_1 = \frac{16}{40} = 0.4, s_1 = \sqrt{\frac{0.4*0.6}{40}} = 0.0775\)
13 of 30 at the other had this infection.
This means that:
\(p_2 = \frac{13}{30} = 0.4333, s_2 = \sqrt{\frac{0.4333*0.5667}{30}} = 0.0905\)
Conduct a test to answer if there is sufficient evidence to conclude that a difference exists between the proportion of students who have ear infections at one school and the other.
At the null hypothesis, we test if there is no difference, that is:
\(H_0: p_1 - p_2 = 0\)
And at the alternate hypothesis, we test if there is difference, that is:
\(H_a: p_1 - p_2 \neq 0\)
The test statistic is:
\(z = \frac{X - \mu}{s}\)
In which X is the sample mean, \(\mu\) is the value tested at the null hypothesis and s is the standard error
0 is tested at the null hypothesis:
This means that \(\mu = 0\)
From the two samples:
\(p = p_1 - p_2 = 0.4 - 0.4333 = -0.0333\)
\(s = \sqrt{s_1^2+s_2^2} = \sqrt{0.0775^2+0.0905^2} = 0.1191\)
Value of the test statistic:
\(z = \frac{X - \mu}{s}\)
\(z = \frac{-0.0333 - 0}{0.1191}\)
\(z = -0.28\)
The test statistic is \(z = -0.28\)
Find the surface area of this triangular promise correct unit

Answers
The surface area of the triangular prism would be =324,000cm²
How to calculate the triangular surface area of the given prism?To calculate the surface area of the triangular prism the formula that should be given would be as follows:
Surface area of triangular prism;
Surface area of triangular prism;= bh+(b1+b2+b3)l
where:
base length = 20cm
height = 15cm
length = 18cm
SA = 20×15(20+15+25)×18
= 300×60×18
= 324,000cm²
Learn more about area here:
https://brainly.com/question/28470545
#SPJ1
it cost $20 for 4 tickets and $35 for 7 play tickets.
Answers
Answer:
$5 per ticket
Step-by-step explanation:
$5 x 7 = $35
$5 x 4 = $20
i dont understand this

Answers
We can Add 7 black beads to make ratio 3 : 1.
Since we can only change the number of black beads, decide how many black beads you will add based on how many white beads there are.
There are three white beads in the picture.
Total beads we will have (b meaning black)b : 3
Ratio black : white beads 3 : 1
Use the common ratio, which is a number that both sides of the original ratio multiply by to get to the new ratio.
Find common ratio by dividing total by ratio white beads: 3/1 = 3
Multiply ratio black beads by common ratio. 3 X 3 = 9
We need 9 black beads in total.
Check answer
9 : 3
Both sides divisible by 3; reduce ratio
= 3 : 1
Which is Correct ratio
Hence, There will be a total of 9 black beads, but we already have 2 black beads:
(9 total) - (2 original) = (7 to add)
Therefore , we need to add 7 black beads.
Learn more about the ratio visit:
https://brainly.com/question/12024093
#SPJ1
How do I solve this
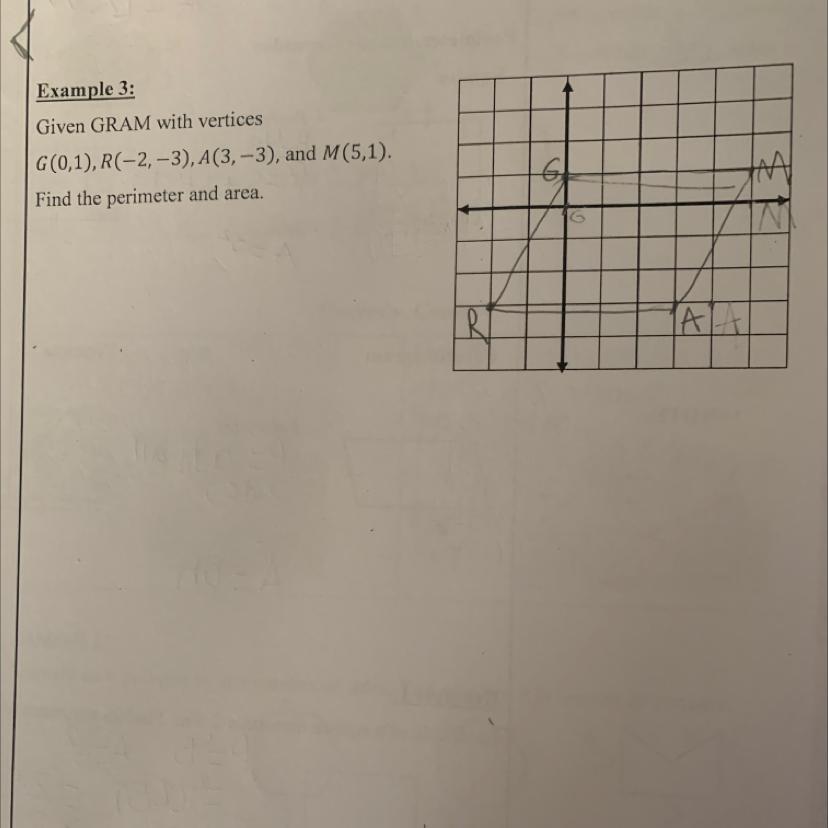
Answers
Answer:
i dont know
Step-by-step explanation:
Can anybody please help me with this one?

Answers
Answer:
0.81
Step-by-step explanation:
The probability that multiple independent events will occur is the product of the probabilities of each of them.
p((<2pm on day 1) & (<2pm on day 2)) = p(<2pm on day 1)×p(<2pm on day 2)
= (0.9)(0.9)
p(before 2 pm on both days) = 0.81
2×3×10 to the 9th power = (1×10 to the 3rd power) (2×3 × 10n)
Answers
Answer:
this is what my calculator said sorry: 1.0077696E16
Step-by-step explanation:
calculator