Two of the sides of a right triangle are 4 and 5. What is the length of the third side? Find all possible answers.
Answers
To find the length of the third side of a right triangle when two sides are given, we can use the Pythagorean theorem. The theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Let's assume the two given sides are 'a' and 'b', and the unknown third side is 'c' (the hypotenuse).
Using the Pythagorean theorem:
c² = a² + b²
Substituting the given values:
c² = 4² + 5²
c² = 16 + 25
c² = 41
To find the length of 'c', we need to take the square root of both sides:
c = √41
So, the length of the third side is √41 (approximately 6.40) when rounded to two decimal places.
Therefore, the possible length of the third side of the right triangle is √41.
Step-by-step explanation:
We will use a phayragoras theorem
a^2 +b^2= c^2
let side1=4 be a
let side2=5 be b
let the 3rd side be the hypotnuous=c
therfore 4^2+5^2=c^2
=16+25=c^2
=41=c^2.
therfore c=√41
Related Questions
Which of the following represents the rotation of the triangle about P by angle A?

Answers
Solution
Rotation means the shape turns as it moves around a fixed point.
In this case, the correct option is

The length of a rectangle is twice its width. Find its lenght and width, if its perimeter is 7 1/3 cm.
Answers
The length of the rectangle is twice its width. If its perimeter is 7 1/3 cm, its length will be 22/9 cm, and the width is 11/9 cm.
Let's assume the width of the rectangle is "b" cm.
According to the given information, the length of the rectangle is twice its width, so the length would be "2b" cm.
The formula for the perimeter of a rectangle is given by:
Perimeter = 2 * (length + width)
Substituting the given perimeter value, we have:
7 1/3 cm = 2 * (2b + b)
To simplify the calculation, let's convert 7 1/3 to an improper fraction:
7 1/3 = (3*7 + 1)/3 = 22/3
Rewriting the equation:
22/3 = 2 * (3b)
Simplifying further:
22/3 = 6b
To solve for "b," we can divide both sides by 6:
b = (22/3) / 6 = 22/18 = 11/9 cm
Therefore, the width of the rectangle is 11/9 cm.
To find the length, we can substitute the width back into the equation:
Length = 2b = 2 * (11/9) = 22/9 cm
So, the length of the rectangle is 22/9 cm, and the width is 11/9 cm.
For more information on the Perimeter of the Rectangle, click:
https://brainly.com/question/13757874
Adam tabulated the values for the average speeds on each day of his road trip as 60.5, 63.2, 54.7, 51.6, 72.3, 70.7, 67.2, and 65.4 mph. The sample standard deviation is 7.309. Adam reads that the average speed that cars drive on the highway is 65 mph. The t-test statistic for a two-sided test would be __________. Answer choices are rounded to the hundredths place.
Answers
Answer:
We accept null hypothesis
Step-by-step explanation:
We assume a normal distribution
The population mean μ₀ = 65 mph
Sample mean μ = 63,2 mph ( calculated from data )
Sample standard deviation σ = 7,309
Sample size n = 8
Degree of freedom is n - 1 8 - 1 = 7
As n < 30 we have to use the t-student test
We will do our test with a confidence interval of 95 % that means α = 5 %
or α = 0,05 and as we are going through a two-tail test α/2 = 0,025
Test Hypothesis:
Null Hypothesis: H₀ μ = μ₀
Alternate Hypothesis Hₐ μ ≠ μ₀
From t-student table for the degree of freedom 7, α/2 = 0,025 two-tail test we find tc
tc = 2,365
And calculate ts as
ts = ( μ - μ₀ ) / σ /√n
ts = ( 63,2 - 65 ) / 7,309/ √8
ts = - 1,8 *2,828/ 7,309
ts = - 5,091 /7,309
ts = - 06965
Now we compare ts and tc
tc = 2,365 or tc = - 2,365 ( by simmetry) tc = -2,37
and ts = -0,06965 ts = - 0,07
As |ts| < |tc|
ts is in the acceptance zone so we accept null hypothesis
Answer:
-0.70
Step-by-step explanation:
For the tabulated value the mean is calculated as:
Mean = (60.5 + 63.2 + 54.7 + 51.6 + 72.3 + 70.7 + 67.2 + 65.4)/8
= 505.6/8
Mean \bar{x}= 63.2
and population mean as assumption u= 65
and given that the sample standard deviation is: s= 7.309
The test statistic is calculated as:
Ζ = Τ –μ 63.2 - 65 = -0.696 -0.70 S
Hence the T statistic would be -0.70
01:
Which expression can be used to model the phrase the sum of three and a number?
Answers
Answer:
3+x
Step-by-step explanation:
sum= addition
a number= a number
Answer:
3+x
eplanation
Calc II Question
Sketch the region enclosed by the given curves and find its area.
Y = lxl , y = x^2 - 2
Answers
Answer:
\(\displaystyle A=\frac{20}{3}\)
Step-by-step explanation:
\(\displaystyle A=\int^2_{-2}(|x|-(x^2-2))\,dx\\\\A=2\int^2_0(x-(x^2-2))\,dx\\\\A=2\int^2_0(-x^2+x+2)\,dx\\\\A=2\biggr(-\frac{x^3}{3}+\frac{x^2}{2}+2x\biggr)\biggr|^2_0\\\\A=2\biggr(-\frac{2^3}{3}+\frac{2^2}{2}+2(2)\biggr)\\\\A=2\biggr(-\frac{8}{3}+2+4\biggr)\\\\A=2\biggr(-\frac{8}{3}+6\biggr)\\\\A=2\biggr(\frac{10}{3}\biggr)\\\\A=\frac{20}{3}\)
Bounds depend on whether you use -x or +x instead of |x|, but you double regardless. See the attached graph for a visual.

Simplify each expression. Write your answer as a complex number.
4i+(2+8i)
(2-7i) - (5-3i)
(5-4i)+(2-7i)
(-3-4i) - (-3+5i
Answers
Answer:
1. 2 + 12i
2. -3 - 4i
3. 7 - 11i
4. -9i
Step-by-step explanation:
just add and subtract like 'i' is a variable and make sure the answer is in the form a+bi
A data set includes weights of garbage discarded in one week from 62 different households. The paired weights of paper and glass were used to obtain the results shown to the right. Is there sufficient evidence to support the claim that there is a linear correlation between weights of discarded paper and glass? Use a significance level of alpha equals 0.05. correlation matrix: Variables Paper Glass Paper 1 0.1853 Glass 0.1853
Answers
Answer:
Because the absolute value of the test statistic is less than the positive critical value, there is not enough evidence to support the claim that there is a linear correlation between the weights of discarded paper and glass for a significance level of α = 0.05.
Step-by-step explanation:
The correlation matrix provided is:
Variables Paper Glass
Paper 1 0.1853
Glass 0.1853 1
Te hypothesis for the test is:
H₀: ρ = 0 vs. H₀: ρ ≠ 0
The test statistic is:
r = 0.1853 ≈ 0.185
As the alternate hypothesis does not specifies the direction of the test, the test is two tailed.
The critical value for the two-tailed test is:
\(r_{\alpha/2, (n-2)}=r_{0.05/2, (62-2)}=r_{0.05/2, 60}=0.250\)
The conclusion is:
Because the absolute value of the test statistic is less than the positive critical value, there is not enough evidence to support the claim that there is a linear correlation between the weights of discarded paper and glass for a significance level of α = 0.05.
Steve inherited $100.000 from his grandmother and deposited it into an account that compounds interest monthlv at a rate of 4.8%. Each month he withdraws $500 from the account. How long will it take him until the account has a balance of $0? Round your answer to the nearest tenth of a year.
Answers
Using the compound interest formula, if the account compounds at 4.8% monthly and he withdraws $500 monthly, it will take Steve 33 years, 7 months (403 months) to reduce $100,000 to a balance (future value) of $0.
What is the difference between the future and present value?The future value is the compounded present value, while the present value is the discounted future value.
However, with periodic withdrawals, a present value that compounds at an interest rate into the future can become $0 (future value) after some periods.
The time (period) Steve reduces his inheritance to $0 can be computed using an online finance calculator as follows:
I/Y (Interest per year) = 4.8%
PV (Present Value) = $100,000
PMT (Periodic Payment) = $-500
FV (Future Value) = $0
Results:
N (# of periods) = 403.164
Sum of all periodic payments = $-201,581.83
Total Interest $101,581.83
Thus, after 403 monthly withdrawals, Steve's inheritance will be reduced to a $0 future value.
Learn more about the future value at https://brainly.com/question/24703884
#SPJ1
IS THIS RIGHT? (28 points easy!!)

Answers
Step-by-step explanation:
yes, the step is correct.
a² = cx | multiply by c
ca² = c²x
I am just not sure how that simplified the equation.
what do you want to achieve ? what's the goal here ?
to solve the equation for x it would be to divide both sides by c, which gives
a²/c = x
Plz answer in 5 minutes

Answers
Answer: 750
Step-by-step explanation:
multiply 75 x 100 you will get 7500 than divide by 10
Which of the following best describes the expression 5(x + 2)? (1 point)
Answers
just distribute each value and multiply 5 to each of the values in the parentheses.
A population of crawfish in a section of the Louisiana bayou increased from 900,000 to 1.2 million between 2010 and 2011. If the population increases by the same percentage between 2011 and 2012, what will the population be in 2012
Answers
Answer: 1,599,960
Step-by-step explanation:
Since the population of crawfish in a section of the Louisiana bayou increased from 900,000 to 1.2 million between 2010 and 2011. The percentage increase in population will be:
= (1.2 million - 900000) / 900000 × 100
= 300000/900000 × 100
= 33.33%
Since the population increases by the same percentage between 2011 and 2012, then the population in 2012 will be:
= (100% + 33.33%) × 1.2 million
= 133.33% × 1.2 million
= 1.3333 × 1.2 million
= 1,599,960
The population in 2012 is 1,599,960
what is the slope of the line on the graph?

Answers
Answer:
1/6
Step-by-step explanation:
A (6,1)
B (12,2)
slope = (2-1)/(12-6)
1/6
7. Find the center of the circle that can be circumscribed about the triangle.-2S82
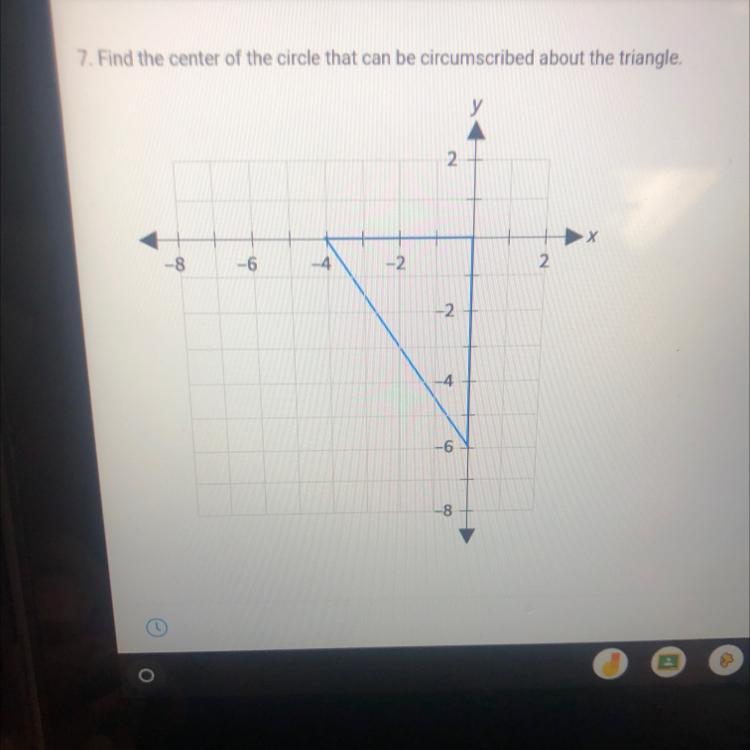
Answers
Answer:
(-2, -3)
Explanation:
To find the center o the circle that can be circumscribed about the triangle, we need to draw the perpendicular bisector of two sides of the triangle. The perpendicular bisector is a line that divides the side into two equal parts and forms an angle of 90 degrees, so in this case, the perpendicular bisector are
The intersection of these lines is the center of the circle. Therefore, the center is (-2, -3)

A man is changing the oil in his car. The instruction manual indicates that the car hold pints of oil. The man only has a cup measure. How many cups equal three pints?
Answers
The volume contained in a cup of oil is a fraction of the volume
contained in a pint of oil.
Correct response:
6 cupsMethod used for the above unit conversionThe measure of the volume of oil the car holds = Pints of oil
The measurement the man has for use = Cups of oil
Required:
The number of cups equal to three pints.
Solution;
1 pint of oil = 2 cups of oil
Therefore;
3 pints of oil = 3 × 2 cups of oil = 6 cups of oil
The number of cups of oil equal to 3 pints of oil is 6 cups of oilLearn more about units conversion here:
https://brainly.com/question/4845674
Mary is planning to survey a sample of women to find out how much money the average woman spent on lipstick last year. What sample size will she need, if she wants to be 95% confident that her sample mean is no more than $4 away from the population mean, and assuming a standard deviation of $20? A. 100
Answers
Answer: The required sample size = 97
Step-by-step explanation:
If prior population standard deviation is known, then the minimum sample size can be computed as:
\(n=(\frac{z^*\times\sigma}{E})^2\)
,where z* = critical z-value
\(\sigma\) = population standard deviation
E = Margin of error
As per given,
\(\sigma=20,\ E= 4\)
Critical value for 95% confidence = 1.96
\(n=(\frac{1.96\times20}{4})^2\\= (1.96\times 5)^2\\= (9.8)^2\\=96.04\approx97\)
Hence, the required sample size = 97
28 is 12 less than k.
Answers
Answer:
k=40
Step-by-step explanation:
subtract 12 from k we would get 28
S vi) The temperature in Gulmerg in Kashmir was-10°C in January and it rose by 44°c to reach the maximum temperature during summer. The maximum temperature during summer in that year was
Answers
The maximum temperature during summer in that year was 34°C.
It's not possible for the maximum temperature in Gulmarg, Kashmir to rise by 44°C during the summer.
A temperature rise of that magnitude would be extremely unusual and potentially dangerous.
However, assuming that the question meant to ask about the difference between the minimum temperature in January and the maximum temperature in summer, we can proceed with the calculation.
The minimum temperature in January was -10°C, and if we add 44°C to it, we get:
-10°C + 44°C = 34°C
Therefore, the maximum temperature during summer in that year was 34°C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ11
Solve for x.
Enter the number that belongs in the green box

Answers
Answer:
x = 45
Step-by-step explanation:
Because these are two congruent triangles inside of each other we can set up an equivalency ratio.
25/35 = x/65
Multiply both sides by 65 to get x alone
65 * 25/35 = x/65 * 65
(65 * 25)/35 = x1
1576/35 = x
x = 45
Hope this helps,
Point Q lies on the circle and has an X-coordinate of 4. Which value could be the y-coordinate for point Q?
Answers
We are not given the radius of the circle or any other relevant data, so I assumed the radius of the circle r=5
Answer:
The y-coordinate of Q is 3
Step-by-step explanation:
Circles and Lines
The figure below shows a circle of radius r=5 and a segment that goes from the center of the circle to a point of the circumference, where x=4.
We can find the y-coordinate of that point by using Pithagora's theorem:
\(r^2=x^2+y^2\)
Solving for y:
\(y^2=r^2-x^2\)
\(y^2=5^2-4^2\)
\(y^2=25-16=9\)
\(y=\sqrt{9}=3\)
The y-coordinate of Q is 3

An engineering scale model shows a church that is 2 inches tall. if the scale is 1 inch = 256 feet, how tall is the actual church
Answers
Answer:
Actual height of church = 512 feet
Step-by-step explanation:
Given:
Scale model;
1 inch = 256 feet
Height of church (Scale model) = 2 inches
Find:
Actual height of church
Computation:
Actual height of church = Height of church (Scale model) x scale length
Actual height of church = 2 inches x 256 feet/inches
Actual height of church = 2 x 256 feet
Actual height of church = 512 feet
noah picked 3 kg of cherries. mia picked half as many cherries as noah. how many total kg of cherries did mia and Noah pick?
Answers
Noah picked 3kg of cherries
if Mia picked half as many cherries as noah, this means Mia picked 1/2 of the cherries Noah picked = 1/2 x 3 =1.5kg
Together the both picked 3 + 1.5 = 4.5 kg of cherries
Find the value of r. 4(x – 3) -5 + 2x = 5(3x - 7) – 9.2

Answers
Answer:
Step-by-step explanation:
what is the answer for 7-4x=2+x+6-5x
Answers
Please someone answer this :D I really need the answer

Answers
Answer:
8.25
Step-by-step explanation:
first substitution
x=4 and y=7
square root(i dont have it) 4(x)7 + 9(x)4 =
square root 28+36 =
square root 64 =
8.246211251
round to 3 significant figure = 8.25
2tan(x/2)- csc x=0 interval [0,2pi)
Answers
Answer:
\(x= \dfrac{\pi}{3}, \;\;x=\dfrac{5 \pi}{3}\)
Step-by-step explanation:
Given trigonometric equation:
\(2 \tan\left(\dfrac{x}{2}\right)- \csc x=0\)
To solve the equation for x in the given interval [0, 2π), first rewrite the equation in terms of sin x and cos x using the following trigonometric identities:
\(\boxed{\begin{minipage}{4cm}\underline{Trigonometric identities}\\\\$\tan \left(\dfrac{\theta}{2}\right)=\dfrac{1-\cos \theta}{\sin \theta}$\\\\\\$\csc \theta = \dfrac{1}{\sin \theta}$\\ \end{minipage}}\)
Therefore:
\(2 \tan\left(\dfrac{x}{2}\right)- \csc x=0\)
\(\implies 2 \left(\dfrac{1-\cos x}{\sin x}\right)- \dfrac{1}{\sin x}=0\)
\(\implies \dfrac{2(1-\cos x)}{\sin x}- \dfrac{1}{\sin x}=0\)
\(\textsf{Apply the fraction rule:\;\;$\dfrac{a}{c}-\dfrac{b}{c}=\dfrac{a-b}{c}$}\)
\(\dfrac{2(1-\cos x)-1}{\sin x}=0\)
Simplify the numerator:
\(\dfrac{1-2\cos x}{\sin x}=0\)
Multiply both sides of the equation by sin x:
\(1-2 \cos x=0\)
Add 2 cos x to both sides of the equation:
\(1=2\cos x\)
Divide both sides of the equation by 2:
\(\cos x=\dfrac{1}{2}\)
Now solve for x.
From inspection of the attached unit circle, we can see that the values of x for which cos x = 1/2 are π/3 and 5π/3. As the cosine function is a periodic function with a period of 2π:
\(x=\dfrac{\pi}{3} +2n\pi,\; x=\dfrac{5\pi}{3} +2n\pi \qquad \textsf{(where $n$ is an integer)}\)
Therefore, the values of x in the given interval [0, 2π), are:
\(\boxed{x= \dfrac{\pi}{3}, \;\;x=\dfrac{5 \pi}{3}}\)

which represents a $3 loss
Answers
Answer:
-$3
Step-by-step explanation:
PLEASE HELP A cylinder with radius 6 feet and height 6 feet has its radius doubled. How many times greater is the volume of the larger cylinder than the smaller cylinder? How many times greater is the volume of the larger cylinder than the smaller cylinder?
Answers
Answer:
16 Times Greater
Step-by-step explanation:
Smaller cylinder:
radius = 6 inches
height = 8 inches
area = (pi)r^2h
area = (3.14)6^2(8)
radius = 24 inches
height = 8 inches
area = (pi)r^2h
area = (3.14)24^2(8)
.
[(3.14)6^2(8)] / [(3.14)24^2(8)]
[6^2(8)] / [24^2(8)]
[6^2] / [24^2]
[36] / [576]
16 times greater
Answer:
Step-by-step explanation:
Smaller cylinder:
h = 6 ft
r = 6 ft
Volume of smaller cylinder = πr²h
= π * 6 * 6 * 6 cubic ft
Bigger cylinder:
r = 6 * 2 = 12 ft
h = 6 ft
Volume of bigger cylinder = π * 12 * 12 * 6 cubic ft
Volume of bigger cylinder = π * 12 * 12 * 6
Volume of smaller cylinder π * 6 * 6 * 6
= \(\frac{2 * 2}{1*1}\\\)
= 4 : 1
The volume of greater cylinder is 4 times than the smaller cylinder.
In a roll of 50 pennies, there are 12 dated 1977. If a penny is drawn at random, what is the probability that it is dated 1977?
Answers
Thus, probability that the one drawn penny is from 1977 dated pennies is 6/25.
Define about the probability:The probability about an occurrence in an experiment is the likelihood that the event will occur. Any event's probability is a number between (including all) "0" and "1".
If an event's probability is represented by P(E), then we get
If and only if the condition E is an impossibility, P(E) = 0.If and just if E is a specific event, then P(E) = 1.Given data:
Total pennies = 50
number of 1977 dated pennies = 12
probability = favourable outcome / total outcome
probability(1977 dated pennies) = number of 1977 dated pennies/ Total pennies
probability(1977 dated pennies) = 12/50
Divide numerator and denominator by 2.
probability(1977 dated pennies) = 6/25
Thus, probability that the one drawn penny is from 1977 dated pennies is 6/25.
Know more about the probability
https://brainly.com/question/13604758
#SPJ1
Will give brainliest

Answers
from,
m = y - y1
x - x1
m = 2 - 5
4 - 1
m = -3 = -1
3
then,
y - y1 = m(x - x1)
using coordinates (1, 5)
y - 5 = -1(x - 1)
y = -x + 1 + 5
y = -x + 6.