two friends are knitting scarves. Each scarf has 3 rectangles and 2/3 of the rectangles have stripes, If the friends are making 10 scarves, how many rectangles do they need? How many rectangles will have stripes?

Answer:

127 ft 3 3/8in

Step-by-step explanation:

Assuming the field is regulation (I can't see the model), the answer is 127 feet and 3 3/8 inches.

Answer:

£ 550

Step-by-step explanation:

C = p(t + 30)

C = 2(245 + 30)

C = 2 (275)                         [using order of operations]

C = 550

Hope this helps!

Answer:

C = £550

Step-by-step explanation:

Given the Cost formula, C = p(t + 30), and p = 2 and t = 245:

Plug in the values of p and t into the formula:

C = p(t + 30)

C = 2(245 + 30)

C = 2(275)

C = 550

Therefore, the total cost is £550.

Answer:

  (a)  twenty-eight ninths, square root of nineteen, cube root of eighty-eight

Step-by-step explanation:

When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.

The attachment shows the ordering, least to greatest, to be ...

  \(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)

__

Additional comment

We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.

One way to do the comparison is to convert these to values that need to have the same root:

  √19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)

  ∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)

The roots will have the same ordering as 19³ and 88².

Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...

  19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859

  88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744

Then the ordering is ...

  28/9 < 19³ < 88²   ⇒   28/9 < √19 < ∛88

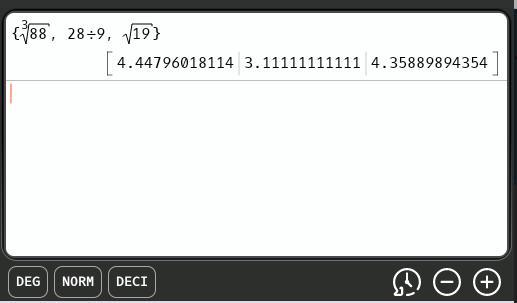
Answer:

the ordering is

28/9 < 19³ < 88²   ⇒   28/9 < √19 < ∛88

Step-by-step explanation:

Step-by-step explanation:

I'm assuming the question is how many miles in total did mary swim.

if this is the case then we just multiply the number of days by the number of miles per day.

Hence,

3/4 × 8 = 6

so 6 miles in total.

make sure to ask if you need any further help

Answer:

4/5

Step-by-step explanation:

Answer:

Some students were asked how many books they were carrying in their backpacks. The data is given in this frequency table. What is the mean number of pens carried by these students in their backpacks?

Pens      Frequency 

0                 4

1                 5

2                 8

3                 4

4                 3

5                 1

A.2

B.3.5

C.4

D.5.5

The linear functions that define their distances are given as follows:

The number of hours after noon in which they will be the same distance away from the stadium is of:

8 hours.

The slope-intercept definition of a linear function is given as follows:

y = mx + b.

In which the parameters are given as follows:

In the context of this problem, the meaning of each parameter is:

They will be the same distance away at the point of intersection of the graph given at the end of the answer, which is of 8 hours.

More can be learned about linear functions at https://brainly.com/question/24808124

#SPJ1

Answer:

Therefore, the solution to the equation -x + 3y = 11 is x = -34/11 and y = 29/11.

Step-by-step explanation:

The given equation is:

-x + 3y = 11

To solve this equation by elimination, we need to add or subtract one or both equations to eliminate one of the variables. In this case, we can eliminate the variable x by adding the equation with another equation that has x with the same coefficient, but opposite sign.

Let's suppose we have another equation with x, for example:

2x + 5y = 7

We can eliminate x by multiplying the first equation by 2 and the second equation by 1, so that the coefficients of x are opposite:

-2x + 6y = 22 (multiply the first equation by -2)

2x + 5y = 7 (the second equation)

Now we can add the two equations to eliminate x:

-2x + 2x + 6y + 5y = 22 + 7

Simplifying the equation, we get:

11y = 29

Dividing both sides by 11, we get:

y = 29/11

Now that we know the value of y, we can substitute it back into one of the original equations to find the value of x. Let's use the first equation:

-x + 3y = 11

Substituting y = 29/11, we get:

-x + 3(29/11) = 11

Simplifying the equation, we get:

-x + 87/11 = 11

Subtracting 87/11 from both sides, we get:

-x = 11 - 87/11

Multiplying both sides by -1, we get:

x = 87/11 - 11

Simplifying the equation, we get:

x = (87 - 121)/11

x = -34/11

Step-by-step explanation:

points on the line: (4, -2) & (-5, 3)

gradient of the line = -5/9

general equation for all straight lines: y = mx + c

substitute one coordinate and the gradient into the equation. 3 = (-5/9)(-5) + c

therefore, c = 2/9

so the general equation is y = (-5/9)x + 2/9

Each piece Measurement of an angle of 120 degrees cut into nine equal lengths with a kerf width of 0.125 would be 14.4583 degrees.

When a particular angle is cut into nine equal parts, the measure of each piece needs to be calculated.

Therefore, it is essential to first calculate the total angle measure and then divide it by the number of parts into which it is being cut.

What is an Angle?

An angle is a geometrical shape that consists of two rays sharing a common endpoint. The common endpoint is known as the vertex, and the two rays are known as the arms of the angle. An angle can be measured in degrees, radians, or gradians. Degrees are the most commonly used unit of measuring angles.How to Calculate Each Piece Measurement of an Angle if Cut into 9 Equal Lengths

To determine each piece measurement of an angle if cut into nine equal lengths, we will need to carry out the following steps:

Step 1: Calculate the total angle measure Suppose the angle being cut into nine equal lengths is an obtuse angle measuring 120 degrees. In that case, the total angle measure will be 120 degrees.

Step 2: Divide the total angle measure by the number of parts into which it is being cut.120 degrees ÷ 9 = 13.3333 degrees

Step 3: Add the kerf width to the piece measurements.0.125 x 9 = 1.125 degrees13.3333 + 1.125 = 14.4583 degrees

Therefore, each piece measurement of an angle of 120 degrees cut into nine equal lengths with a kerf width of 0.125 would be 14.4583 degrees.

For more questions on Measurement .

https://brainly.com/question/27233632

#SPJ8

Answer:

I believe the new price is 203.

Step-by-step explanation:

Answer:

lkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk

Step-by-step explanation:

The equation that defines the proportional relationship is: y = 26x.

Proportional relationship can be defined as the relation between variables x and y, whereby their ratios are the same. The equation can be modelled as, y = kx, where k is the unit rate.

Let's check out the ratio of distance travelled to gallon of gas used:

26:1 = 26/1 = 26

130:5 = 130/5 = 26

The unit rate is k = 26.

The equation would be: y = 26x

They have equivalent ratios, therefore, the relationship between distance travelled and gas usage defines a proportional relationship.

Learn more about proportional relationship on:

https://brainly.com/question/15618632

#SPJ6

29 years from now, the father will be 49 years old.

Let's start by setting up the given information:

Currently, the father is 20 years old, and the son is 5 years old.

In 10 years, the father will be twice as old as the son.

The father is currently four times as old as the son.

Determine the age of the father and son in 10 years:

In 10 years, the father's age will be 20 + 10 = 30 years.

In 10 years, the son's age will be 5 + 10 = 15 years.

Write equations based on the given information:

The father's age in 10 years will be twice the son's age in 10 years: 30 = 2 × 15.

The father's current age is four times the son's current age: 20 = 4 × 5.

Solve the equations:

From the second equation, we find that the son's current age is 5 years.

Plugging this value into the first equation, we get: 30 = 2 × (5 + 10).

Simplifying further, we have: 30 = 2 × 15, which is true.

Determine the current age of the son in 29 years:

The son's current age is 5 years.

Adding 29 years to the son's current age, we find that the son will be 5 + 29 = 34 years old.

Determine the current age of the father in 29 years:

The father's current age is 20 years.

Adding 29 years to the father's current age, we find that the father will be 20 + 29 = 49 years old.

Therefore, 29 years from now, the father will be 49 years old.

for such more question on age

https://brainly.com/question/25863198

#SPJ11

to get the equation of any straight line, we simply need two points off of it, so let's use the provided ones

\(f(-3)=5\implies \begin{cases} x=-3\\ y=5 \end{cases}\hspace{5em}f(6)=11\implies \begin{cases} x=6\\ y=11 \end{cases} \\\\[-0.35em] ~\dotfill\\\\ (\stackrel{x_1}{-3}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{6}~,~\stackrel{y_2}{11}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{11}-\stackrel{y1}{5}}}{\underset{run} {\underset{x_2}{6}-\underset{x_1}{(-3)}}} \implies \cfrac{6}{6 +3} \implies \cfrac{ 6 }{ 9 } \implies \cfrac{2 }{ 3 }\)

\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{5}=\stackrel{m}{ \cfrac{2 }{ 3 }}(x-\stackrel{x_1}{(-3)}) \implies y -5 = \cfrac{2 }{ 3 } ( x +3) \\\\\\ y-5=\cfrac{2}{3}x+2\implies {\Large \begin{array}{llll} y=\cfrac{2}{3}x+7 \end{array}}\)

By definition, a monomial is a polynomial that has one term.

In this case you have these monomials:

In order to find the Greatest Common Factor (GCF) of this pair of monomials (which is also known as Greatest Common Divisor), you can apply the steps shown below:

Step 1. You need to descompose each monomial into its prime factors, as following:

Step 2. Now you must choose the common factors with the lowest exponents and then you must multiply them. The product will be the Greatest Common Factor. Then:

The answer is:

Answer:

A correctly shows the location of all the given values.

Step-by-step explanation:

The main difference can be found with the value -2 \(\frac{3}{4}\). This value would be less than -2 so the dot should be close to the middle line between -2 and -4.

Hope this helps~!

Answer:

A

Step-by-step explanation:

A) -4, -2 3/4, 1/2 , 1 1/4

B) -4, -2 1/4, 1/2 , 1 1/4

C) -4, -1 1/4, 1/2, 2 1/4

D) -4, -1/2, 1/2, 2 3/4

The motivations for producers and consumers in the black market are largely driven by financial incentives and a desire to avoid legal consequences.

The black market refers to the illegal trade of goods and services that are not permitted by law, such as drugs, counterfeit items, and stolen goods. Producers and consumers in the black market are motivated by a variety of factors, including:

High profits, Producers in the black market can earn higher profits than they would in legal markets due to the lack of regulation and taxes.

Escaping legal consequences: Producers and consumers may participate in the black market to avoid legal consequences, such as fines or imprisonment, for engaging in illegal activities.

Limited availability, Some goods and services are only available on the black market due to legal restrictions or limited supply.

Low prices, Consumers in the black market can often purchase goods and services at lower prices than in legal markets due to the lack of taxes and regulations.

Desire for anonymity, The black market can provide anonymity for both producers and consumers, allowing them to engage in illegal activities without fear of detection or retribution.

However, participating in the black market also comes with significant risks, including the possibility of arrest, fines, and even violence.

To learn more about financial incentives here:

https://brainly.com/question/29767675

#SPJ1

Answer:

f(x) = x³ - 4x + 6

f'(x) = 3x² - 4

a) f'(2) = 3(2²) - 4 = 12 - 4 = 8

6 = 8(2) + b

6 = 16 + b

b = -10

y = 8x - 10

b) 3x² - 4 = 0

3x² = 4, so x = ±2/√3 = ±(2/3)√3

= ±1.1547

f(-(2/3)√3) = 9.0792

f((2/3)√3) = 2.9208

c) 3x² - 4 = 8

3x² = 12

x² = 4, so x = ±2

f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6

6 = -2(8) + b

6 = -16 + b

b = 22

y = 8x + 22

f(2) = 6

y = 8x - 10

The equation perpendicular to the tangent is y = -1/8x + 25/4

-The smallest slope on the curve is 2.92

The curve has the smallest slope at the point (1.15, 2.92)

The equations at tangent points are y = 8x + 16 and  y = 8x - 16

From the question, we have the following parameters that can be used in our computation:

y = x³ - 4x + 6

Differentiate

So, we have

f'(x) = 3x² - 4

The point is (2, 6)

So, we have

f'(2) = 3(2)² - 4

f'(2) = 8

The slope of the perpendicular line is

Slope = -1/8

So, we have

y = -1/8(x - 2) + 6

y = -1/8x + 25/4

We have

f'(x) = 3x² - 4

Set to 0

3x² - 4 = 0

Solve for x

x = √[4/3]

x = 1.15

So, we have

Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6

Smallest slope = 2.92

So, the smallest slope is 2.92 at (1.15, 2.92)

Here, we set f'(x) to 8

3x² - 4 = 8

Solve for x

x = ±2

Calculate y at x = ±2

y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)

y = (2)³ - 4(2) + 6 = 6: (2, 0)

The equations at these points are

y = 8x + 16

y = 8x - 16

Read more about tangent lines at

https://brainly.com/question/21595470

#SPJ1

The inequality tha calculates the possible values of x is x < 2

From the question, we have the following parameters that can be used in our computation:

The figure

Where, we have

3x + 2 < 10

And, we have

2x + 6 < 10

Evaluate the expressions

So, we have

3x < 8 and 2x < 4

Evaluate

x < 8/3 and x < 2

Hence, the inequality tha calculates x is x < 2

Read more about inequality at

https://brainly.com/question/32124899

#SPJ1

The surface area of a cube that has a width of 25 centimeters is 3750 cm².

It should be noted that surface area simply implies the measure of the total area that the surface of an object occupies.

In this case, the surface area of a cube is measured as 6a² where a = side

In this case, the side is 25. Therefore, the surface area will be:

= 6a²

= 6 × 25²

= 3750 cm²

Learn more about surface area on:

brainly.com/question/1297098

#SPJ1

The inverse of the function → f(x) = 2x + 5  is → f⁻¹(x) = (x/2) - (5/2).

Inverse of a function can be calculated by following the steps mentioned below -

According to the question, the equation given is as follows

y = f(x) = 2x + 5

y = 2x + 5

Replace 'y' with 'x', we get -

x = 2y + 5

Now, solve for y -

2y = x - 5

y = (x/2) - (5/2)

Replace 'y' with f⁻¹(x) -

f⁻¹(x) = (x/2) - (5/2)

Hence, the inverse of the function → f(x) = 2x + 5  is → f⁻¹(x) = (x/2) - (5/2).

To solve more questions on inverse of function, visit the link below-

brainly.com/question/28229665

#SPJ1

Answer:

6 cm

Step-by-step explanation:

Volume of a prism= Length X Width x height

750 = 25 x 5 x h

750= 125h

750/125 = 125h/125

h= 6

Answered by Gauthmath

Answer:

1 gal 9 qt

Step-by-step explanation:

Answer:

1.75 US Gallons

Step-by-step explanation:

(3 gal 2 qt) - (1 gal 3 qt) =

1.75 US gallons

Answer:

Step-by-step explanation:

7

The frequency is just a way for us to know how often an event occurred.

Please find attached the frequency distribution table.

Class with greatest frequency is; Class 30 - 39

Class with least frequency is; Class 20 - 29

Now, we are told to construct a frequency distribution for the given data using 5 classes.

This means the 5 classes will be as follows;

0 - 9

10 - 19

20 - 29

30 - 39

40 -49

0 - 9; 5

10 - 19; 4

20 - 29; 1

30 - 39; 6

40 -49; 4

Class with greatest frequency is; Class 30 - 39

Class with least frequency is; Class 20 - 29

This means the sample size is; n = 5 + 4 + 1 + 6 + 4 = 20

Thus for the classes, we have Rel. Freq as;

0 - 9; 5/20 =0.25

10 - 19; 4/20 = 0.2

20 - 29; 1/20 = 0.05

30 - 39; 6/20 = 0.3

40 -49; 4/20 = 0.2

Thus, we have;

0 - 9; (0 + 9)/2 = 4.5

10 - 19;  (10 + 19)/2 = 14.5

20 - 29;  (20 + 29)/2 = 24.5

30 - 39;  (30 + 39)/2 = 34.5

40 -49;  (40 + 49)/2 = 44.5

Thus, we have;

0 - 9; 5

10 - 19; 4 + 5 = 9

20 - 29; 1 + 9 = 10

30 - 39; 6 + 10 = 16

40 -49; 4 + 16 = 20

Read more at; brainly.com/question/17114842

Answer:

48

Step-by-step explanation:

4*2*3 for the 4 flaps

2*4*3 for the 2 tops

(4*2*3) + (2*4*3) = 48

Answer:

52 square inches

Step-by-step explanation:

to find the surface area of a rectangular prism the formula is

S.A.=2(l*w+l*h+w*h)

2(4*3+4*2+3*2)

=52 square inches

here l is length w is width and h is height

By analyzing the graph and evaluating the objective function at each vertex of the feasible region, we can find the optimal solution, which is the vertex that maximizes the objective function z = 3x + y.

To find the optimal solution of the given problem using the graphical method, we need to plot the feasible region determined by the given constraints and then identify the point within that region that maximizes the objective function.

Let's start by graphing the constraints:

1. Plot the line 2x - y = 5. To do this, find two points on the line by setting x = 0 and solving for y, and setting y = 0 and solving for x. Connect the two points to draw the line.

2. Plot the line -x + 3y = 6 using a similar process.

3. The x-axis and y-axis represent the constraints x ≥ 0 and y ≥ 0, respectively.

Next, identify the feasible region, which is the region where all the constraints are satisfied. This region will be the intersection of the shaded regions determined by each constraint.

Finally, we need to identify the point within the feasible region that maximizes the objective function z = 3x + y. The optimal solution will be the vertex of the feasible region that gives the highest value for the objective function. This can be determined by evaluating the objective function at each vertex and comparing the values.

Note: Without a specific graph or additional information, it is not possible to provide the precise coordinates of the optimal solution in this case.

For more such questions on graph

https://brainly.com/question/19040584

#SPJ8

The area of the circle inscribed inside the square is 64π cm²

An equation is an expression that shows the relationship between two or more numbers and variables.

The circle inside the square as shown in the diagram have a diameter of 16 cm. Hence:

Radius = diameter / 2 = 16/2 = 8 cm

Area of circle = π * radius² = π * 8² = 64π cm²

The area of the circle inscribed inside the square is 64π cm²

Find out more on equation at: https://brainly.com/question/13763238

#SPJ1