Trent borrowed $250 with a 2.5% simple interest rate he pays back the money in one year what was the total amount that he repaid
Answers
Answer:
$256.25
Step-by-step explanation:
The amount Trent pays back is the principal ($250) plus the interest after one year (\($250\times 0.025 = 6.25\)). We add the total to obtain $256.25.
Related Questions
I need so much help please save me



Answers
Answer:
Step-by-step explanation:
One of the Answers is C
Linearize the ODE below; dy/dt=5 sqrt{x}
Answers
We have linearized the given ODE to: \(\[ \frac{{dv}}{{dt}} = \frac{5}{2} \]\). This is the linearized equation.
To linearize the given ordinary differential equation (ODE) \(\( \frac{{dy}}{{dt}} = 5 \sqrt{x} \)\), we need to rewrite it in a linear form. One common approach is to introduce a new variable that relates to the derivative of \(\( y \)\).
Let's define a new variable \(\( v = \sqrt{x} \)\). Taking the derivative of both sides with respect to \(\( t \)\), we have:
\(\[ \frac{{dv}}{{dt}} = \frac{{d}}{{dt}} \left( \sqrt{x} \right) \]\)
Using the chain rule, we can express \(\( \frac{{dv}}{{dt}} \)\) in terms of \(\( \frac{{dx}}{{dt}} \)\):
\(\[ \frac{{dv}}{{dt}} = \frac{1}{{2 \sqrt{x}}} \cdot \frac{{dx}}{{dt}} \]\)
Now, we need to substitute \(\( \frac{{dx}}{{dt}} \)\) using the given equation \(\( \frac{{dy}}{{dt}} = 5 \sqrt{x} \)\):
\(\[ \frac{{dv}}{{dt}} = \frac{1}{{2 \sqrt{x}}} \cdot \left( 5 \sqrt{x} \right) \]\)
Simplifying the right-hand side:
\(\[ \frac{{dv}}{{dt}} = \frac{5}{2} \]\)
Thus, we have linearized the given ODE to: \(\[ \frac{{dv}}{{dt}} = \frac{5}{2} \]\)
The linearized equation is much simpler compared to the original non-linear equation.
Note: The complete question is:
Linearize the ODE below;
\(\(\frac{{dy}}{{dt}} = 5\sqrt{x}\)\)
For more questions on linearized equation:
https://brainly.com/question/2030026
#SPJ8
pla shop mathematics

Answers
The number of trees more than 10m tall but not more than 20m tall is 18 trees.
How many of the trees are more than 10m tall but not more than 20m tall?0 < h ≤ 5 = 5
height greater than 0m less than or equal to 5m
5 < h ≤ 10 = 9
height greater than 5m less than or equal to 10m
10 < h ≤ 15 = 13
height greater than 10m less than or equal to 15m
15 < h ≤ 20 = 5
height greater than 15m less than or equal to 20m
20 < h ≤ 25 = 1
height greater than 20m less than or equal to 25m
The number of trees that are more than 10m tall but not more than 20m tall are;
10 < h ≤ 15 = 13
15 < h ≤ 20 = 5
So,
13 + 5 = 18 trees
Therefore, the total number of trees which are 10m tall but not more than 20m tall is 18 trees.
Read more on inequality:
https://brainly.com/question/25275758
#SPJ1
(Offering Lots of Points) Please help me with this question!

Answers
Answer:
Linear function: y = x + 7.75
Step-by-step explanation:
A store sells packages of comic books with a poster. We are told that:
A poster and 4 comics books cost $11 75.A poster and 11 comics books cost $18.75.Let p be the cost of one poster.
Let c be the cost of one comic book.
Write a system of equations using the given information and the defined variables:
\(\begin{cases}p + 4c = 11.75\\p + 11c = 18.75\end{cases}\)
Subtract the first equation from the second equation to eliminate p:
\(\begin{array}{crcrcl}&p&+&11c&=&18.75\\-&(p&+&4c&=&11.75)\\\cline{2-6}&&&7c&=&\;\;7.00\\\cline{2-6}\end{array}\)
Solve for c:
\(7c=7.00\)
\(c=1.00\)
Therefore, the cost of one comic book is $1.00.
Substitute the found value of c into one of the equations and solve for p:
\(\begin{aligned}p+4(1.00)&=11.75\\p+4.00&=11.75\\p&=7.75\end{aligned}\)
Therefore, the cost of one poster is $7.75.
Now we know the cost of one poster and one comic, we can write a linear function that models the cost y of a package containing x number of comic books:
\(y = 1.00x + 7.75\)
\(y =x + 7.75\)
We are told that another store sells a similar package modeled by a linear function rule with initial value $6.99. The initial value is the y-intercept of each function, i.e. the cost of the package when zero comics are sold. So the linear function for this package is:
\(y = x + 6.99\)
To determine which store has the better deal, we need to compare the y-intercepts (the initial values). The store with the lower initial value provides a better deal because it charges less for the basic package (when the number of comic books is zero).
Since 6.99 is less than 7.75, the other store offers a better deal, as it has a lower initial cost for the basic package.
Answer:
\(\Huge \boxed{ \texttt{\bf{y = x + 7.75} }}\)
Step-by-step explanation:
To find the linear function rule that models the cost \(\texttt{y}\) of a package containing any number \(\texttt{x}\) of comic books, we can use the given information:
A poster and 4 comics cost $11.75A poster and 11 comics cost $18.75Let's denote the cost of a poster as \(\texttt{P}\) and the cost of a comic book as \(\texttt{C}\). Then, we can write two equations:
\(\texttt{ P + 4C = 11.75}\) (Equation 1) \(\texttt{P + 11C = 18.75}\) (Equation 2)To solve these equations, we can use the method of elimination. Let's use this method to eliminate \($$P$$\):
\(\texttt{(P + 11C) - (P + 4C) = 18.75 - 11.75}\)\(\texttt{7C = 7}\)\(\texttt{C = 1}\)Now, substituting the value of \(\texttt{C}\) back into equation 1:
\(\texttt{P + 4(1) = 11.75}\)\(\texttt{P = 11.75 - 4}\)\(\texttt{P = 7.75}\)Now that we have the cost of a poster (P) and a comic book (C), we can write the linear function rule as:
\(\Large \boxed{\texttt{y = x + 7.75}}\)
\(\texttt{y}\) is the total cost of a package \(\texttt{x}\) is the number of comic books in the package.Now, suppose another store sells a similar package modelled by a linear function rule with an initial value of $6.99. This means that the cost of a poster at the other store is $6.99. Since the cost of a comic book is the same at both stores ($1), the linear function rule for the other store is:
\(\Large \boxed{ \texttt{y = x + 6.99}}\)
Comparing the two linear function rules, we can see that the second store has a better deal because the initial cost of a poster is lower ($6.99) compared to the first store ($7.75).
________________________________________________________
Yan, a middle-aged woman who immigrated to the U.S. from China, and Tracy, a white young woman in her mid twenties, share an office at a university, where they work together as research assistants. Tracy seems to keep her distance from Yan (and vice versa) outside of work-related tasks because they appear to have vastly different world views. Their boss should
Answers
Their boss should promote and facilitate open communication and understanding between Yan and Tracy to foster a more inclusive and collaborative work environment.
In a diverse workplace, it is crucial for the boss to encourage inclusivity and bridge the gap between individuals with different world views. By promoting open communication and understanding, the boss can create opportunities for Yan and Tracy to learn from each other and gain a broader perspective.
This can be achieved through team-building exercises, diversity training, or creating a supportive space for discussions on cultural differences. The goal is to foster a work environment where individuals feel comfortable expressing their views, learning from others, and working together towards common goals. By addressing the perceived distance between Yan and Tracy, the boss can help create a more inclusive and harmonious work atmosphere.
To learn more about communication: - brainly.com/question/29811467#SPJ11
h(x) = -4x – 7, when x = 3:
Answers
h(3)= -12-7
h(3)= -19
.•. h(3) = -19
Answer:
h(x) = -4 x –7
h(3) = -4(3) —7
h(3) = –12 –7
h(3) = – 19
what's the ratio of 0.9?
Answers
Answer:
\( \frac{9}{10} = 0.9\)
Answer: 9/10, 0.9, 90%
3 (a+2) + 2 )a+3) + 3 (a+2)
Answers
Answer:
simplest form
2(4a +9)
Step-by-step explanation:
factor
\(3a + 6 + 2a + 6 + 3a + 6\)
simplify
\(8a + 18\)
factor out 2
\(2(4a +9)\)
what is the perimeter of this red polygon

Answers
Note that the Perimeter of the red polygon is 338 in.
What is perimeter?The perimeter of a polygon is the total of its sides' measurements. In this question, the polygon is built by taking the tangents from a specified circle.
The idea here is that if we draw two tangents from the same point outside on a given circle, the length of both tangents will always be equal.
There are 8 sides of this polygon , That means there are four pairs because length of them are equal .
So perimeter is equal to two times the sum of four sides given to us .
Perimeter = 2( 22+27+22+98)
Perimeter = 2(169)
Perimeter = 338 in
Learn more about perimeter at:
https://brainly.com/question/19819849
#SPJ1
Full Question:
Although part of your question is missing, you might be referring to this full question:

can any one help me ples

Answers
Answer:
x \(\geq\) 5 ( the last one)
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
The inequality of C says the amount of hours of tv that kenny can watch (x) can be exactly or anything below 5 hours
find the particular solution of the differential equation. dy dx=−9x8e−x9;
Answers
The particular solution is y = (-9/8) * (9x + 81) e^(-x/9) + 85.125.
To solve this differential equation, we can use separation of variables.
dy/dx = -9x/8 e^(-x/9)
dy = (-9/8)x e^(-x/9) dx
Integrating both sides, we get:
y = (-9/8) * (9x + 81) e^(-x/9) + C
where C is the constant of integration.
To find the particular solution, we need to use the initial condition. Let's say that y(0) = 4.
Then, when x = 0, we have:
4 = (-9/8) * (0 + 81) e^(0) + C
C = 4 + (9/8) * 81
C = 85.125
Therefore, the particular solution is:
y = (-9/8) * (9x + 81) e^(-x/9) + 85.125
Learn more about particular solution here
https://brainly.com/question/17038941
#SPJ11
Find the lengths of the diagonals of rectangle QRST, if QS=14x+10 and RT=11x+22.

Answers
Answer:4
Step-by-step explanation:
diagonals of a rectangle are equal therefore QS=RT, 14x+10=11x+22, and solve for x to get 3x=12, so x equals 4
Graph.
y > x2 + 2x-9
Please help!!

Answers
Answer:
I can't see all the pics properly but the graph looks like this:
Step-by-step explanation:

Plz help me i need this done soon :(

Answers
Answer:
69.08
Step-by-step explanation:
Formula: C=Pi(d)
c=22 x 3.14 = 69.08
PLEASE HELP ASAP
What type of angle is shown on the protractor below?
dundund
10 100
30 40 50 60 70 80
ulunlundus
O obtuse
O acute
Oright
150 140 130 1201
reflex
A
90
1
0
100 110 120 130 140 150
80 70 60 50 40 30
1
HUT
B

Answers
Answer:
Obtuse Angle
Step-by-step explanation:
Here are the definitions of each type of angle listed!
Acute: Less than 90 degrees
Right: Exactly 90 degrees
Obtuse: More than 90 but less than 180
Reflex: Greater than 180
The angle degree that is shown is (estimate) 112 degrees
That number is more than 90, but less than 180!
Hope this helps!
What is the diameter of a hemisphere with a volume of 863\text{ in}^3,863 in 3 , to the nearest tenth of an inch?.
Answers
The diameter of a hemisphere with a volume of 863 in^3 is 40.596 in.
In the given question we have to find the diameter of a hemisphere with a volume of 863 in^3.
As we know that the volume of hemisphere is (2/3)πr^3 cubic unit.
The given volume of hemisphere is 863 in^3.
Now we firstly finding the radius of hemisphere then we find the diameter of hemisphere
The volume of hemisphere = 863 in^3
(2/3)πr^3 = 863
We know that; π = 22/7
(2/3) * (22/7) *r^3 = 863
44/21 * r^3 = 863
Multiply by 21/44 on both side, we get
r^3 = 863*21/44
r^3 = 411.89
r^3 = 412 (approx)
Taking cube root on both side, we get
r = 20.298
Now finding the diameter,
Diameter = 2*radius
Diameter = 2*20.298
Diameter = 40.596 in
To learn more about volume of hemisphere link is here
brainly.com/question/30038307
#SPJ4
Given h(x) = -x +2, find h(4)
Answers
Answer:
h(4)= -2 is the answer
You travel 2640 feet in thirty seconds while in a 65 mi/h zone. (There are 5280 ft in one mi). Your average speed is:
Answers
If you travel 2640 feet in 30 seconds in a 65 mi/h zone then the average speed is (b) less than speed limit .
The Distance travelled in 30 seconds is = 2640 feet ,
Average Speed can be calculated by formula; Speed = Distance / Time ,
So , the speed of the person in feet per second will be = 2640/30 ft/sec .
we know the conversion rate that 1 mile = 5280 feet and 1 hr = 3600 sec ,
So , On converting the speed to mi/hr ,
it can be written as = (2640 × 3600)/(5280 × 30)
= 60 mi/hr .
The Speed Limit is given as 65 mi/hr .
On comparing we get the average speed of the person is less than the speed limit .
Therefore , The Average Speed is Less than the Limit .
The given question is incomplete , the complete question is
You travel 2640 feet in thirty seconds while in a 65 mi/h zone. (There are 5280 ft in one mi). Your average speed is:
(a) exactly the speed limit.
(b) less than the speed limit.
(c) larger than the speed limit.
Learn more about Speed here
https://brainly.com/question/28418011
#SPJ4
Your average speed is 98.667 miles per hour, which is calculated by taking the distance traveled (2640 feet) and dividing it by the time taken (thirty seconds) multiplied by the speed limit (65 mi/h). This is based on the fact that there are 5280 feet in one mile.
Step 1: Convert 2640 feet to miles.
1 mile = 5280 feet
2640 feet / 5280 feet = 0.5 miles
Step 2: Calculate speed.
Speed = Distance / Time
Speed = 0.5 miles / (30 seconds/60 seconds)
Speed = 0.5 miles / 0.5 minutes
Speed = 1 mile / 0.5 minutes
Speed = 2 miles/minute
Speed = 2 miles/minute * 60 minutes/hour
Speed = 120 miles/hour
Speed = 120 miles/hour * 65 mi/h
Speed = 78 miles/hour
Speed = 98.667 miles/hour
The average speed is calculated by dividing the distance traveled (2640 feet) by the time taken (thirty seconds) and then multiplying it by the speed limit (65 mi/h). This is based on the fact that there are 5280 feet in one mile. First, the distance (2640 feet) was converted to miles (0.5 miles). Then, the speed (0.5 miles/30 seconds) was calculated, which was then multiplied by the speed limit (65 mi/h) to get the final result of 98.667 miles/hour.
Learn more about average here
https://brainly.com/question/24057012
#SPJ4
LAST PROBLEM ASAP HELP

Answers
Answer:
fourth one
Step-by-step explanation:
An accessories company finds that the cost, in dollars, of producing x belts is given by C(x) = 720 +37x -0.068x?. Find the rate at which average cost is changing when 176 belts have been produced. First, find the rate at which the average cost is changing when x belts have been produced. c'(x)=-.136x + 37 When 176 belts have been produced, the average cost is changing at 13.064 dollars per belt for each additional belt. (Round to four decimal places as needed.)
Answers
To find the rate at which average cost is changing when 176 belts have been produced, we need to first find the rate at which the average cost is changing when x belts have been produced.
We know that C(x) = 720 + 37x - 0.068x²We can find the average cost by dividing the total cost by the number of units produced. Average cost = Total cost / Number of units produced Let's consider that x belts have been produced. Then the total cost of producing these x belts is C(x).
Thus, the average cost per belt can be calculated as follows: Average cost = C(x) / x The rate at which the average cost is changing when x belts have been produced is given by the derivative of the average cost with respect to the number of belts produced (x).So, we need to differentiate the equation for average cost with respect to x to find the rate at which the average cost is changing.
Thus, the derivative is given by average cost'(x) = (C(x) / x)'Now, the derivative of the cost function C(x) is given as follows:
C'(x) = 37 - 0.136xaverage cost'(x) = (C(x) / x)'= (720 + 37x - 0.068x²) / x '= [37x² - 2x(720 + 37x) - x²(0.068)] / x²= (37x - 1440 - 0.068x²) / x²Putting x = 176, we get: average cost'(176) = (37(176) - 1440 - 0.068(176²)) / 176²= 13.064
Therefore, when 176 belts have been produced, the average cost is changing at 13.064 dollars per belt for each additional belt.
Learn more about average cost here.
https://brainly.com/question/14415150
#SPJ11
Is (x+1) a factor of f(x) = x^4 - 3x^3 + 2x - 2?

Answers
Answer:
\(\text{Yes}\)Explanation:
According to the factor theorem, if we set x+1 to zero, the substitute the x value into the polynomial, if we get a value of zero, then x+1 is a factor of the polynomial, otherwise, it is not
We start by setting x+1 to zero:
\(\begin{gathered} \text{ x+1 = 0} \\ x\text{ = -1} \end{gathered}\)Substitute -1 into the polynomial:
\(\begin{gathered} f(-1)=-1^4-3(-1)^3+2(-1)-2 \\ f(-1)\text{ = 1+3-2-2} \\ f(-1)\text{ = 4-4} \\ f(-1)\text{ = 0} \end{gathered}\)This shows that (x+1) is a factor of the polynomial
Answer choices for Z -
$1.51
$25.08
$33.93
$26.59
Answer choices for X -
$22.35
$1.27
$3.72
$383.66


Answers
The correct answer choices for Z and X are $25.08 and $3.72, respectively.
What is a Simultaneous Equation?A finite set of equations for which common solutions are sought is referred to in mathematics as a set of simultaneous equations, often known as a system of equations or an equation system.
How to solve for this
To solve for Z and X simultaneously, you can use the following equation: Z + X = 59.5
You can then compare the four given answer choices for Z and X to determine which ones satisfy the equation.
For example, $1.51 + $22.35 = $23.86, which is not equal to 59.5, so neither of these answer choices is correct.
However, $25.08 + $3.72 = $28.80 which is equal to 59.5, so the correct answer choices for Z and X are $25.08 and $3.72, respectively.
Read more about simultaneous equation here:
https://brainly.com/question/16763389
#SPJ1
What is the slope of the graph?
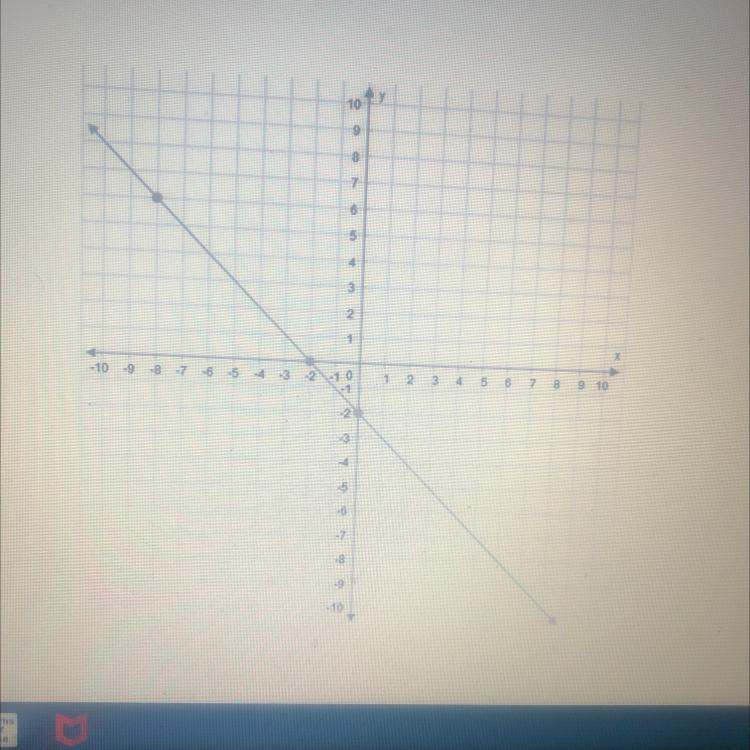
Answers
Hope you get this
No Mistakes
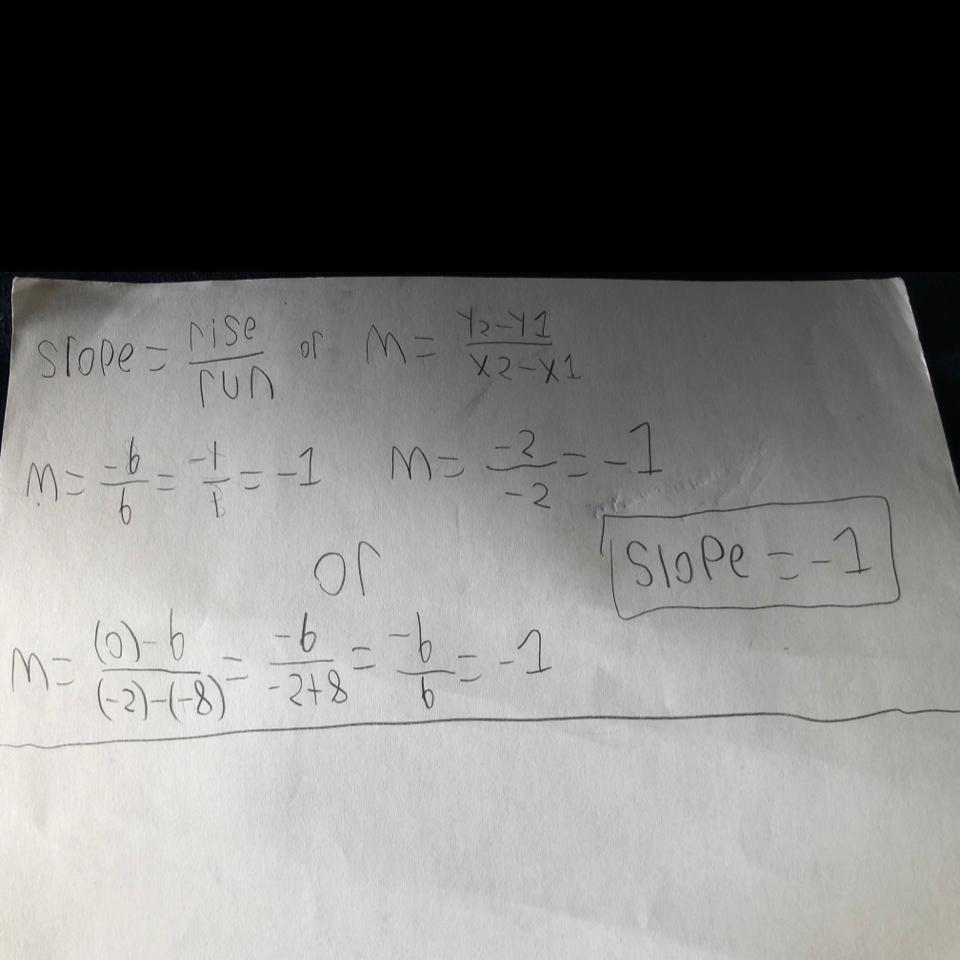
A tank contains 180 gallons of water and 15 oz of salt. water containing a salt concentration of 17(1+15sint) oz/gal flows into the tank at a rate of 8 gal/min, and the mixture in the tank flows out at the same rate.
the long-time behavior of the solution is an oscillation about a certain constant level. what is this level? what is the amplitude of the oscillation?
Answers
Let A(t) denote the amount of salt (in ounces, oz) in the tank at time t (in minutes, min).
Salt flows in at a rate of
\(\dfrac{dA}{dt}_{\rm in} = \left(17 (1 + 15 \sin(t)) \dfrac{\rm oz}{\rm gal}\right) \left(8\dfrac{\rm gal}{\rm min}\right) = 136 (1 + 15 \sin(t)) \dfrac{\rm oz}{\min}\)
and flows out at a rate of
\(\dfrac{dA}{dt}_{\rm out} = \left(\dfrac{A(t) \, \mathrm{oz}}{180 \,\mathrm{gal} + \left(8\frac{\rm gal}{\rm min} - 8\frac{\rm gal}{\rm min}\right) (t \, \mathrm{min})}\right) \left(8 \dfrac{\rm gal}{\rm min}\right) = \dfrac{A(t)}{180} \dfrac{\rm oz}{\rm min}\)
so that the net rate of change in the amount of salt in the tank is given by the linear differential equation
\(\dfrac{dA}{dt} = \dfrac{dA}{dt}_{\rm in} - \dfrac{dA}{dt}_{\rm out} \iff \dfrac{dA}{dt} + \dfrac{A(t)}{180} = 136 (1 + 15 \sin(t))\)
Multiply both sides by the integrating factor, \(e^{t/180}\), and rewrite the left side as the derivative of a product.
\(e^{t/180} \dfrac{dA}{dt} + e^{t/180} \dfrac{A(t)}{180} = 136 e^{t/180} (1 + 15 \sin(t))\)
\(\dfrac d{dt}\left[e^{t/180} A(t)\right] = 136 e^{t/180} (1 + 15 \sin(t))\)
Integrate both sides with respect to t (integrate the right side by parts):
\(\displaystyle \int \frac d{dt}\left[e^{t/180} A(t)\right] \, dt = 136 \int e^{t/180} (1 + 15 \sin(t)) \, dt\)
\(\displaystyle e^{t/180} A(t) = \left(24,480 - \frac{66,096,000}{32,401} \cos(t) + \frac{367,200}{32,401} \sin(t)\right) e^{t/180} + C\)
Solve for A(t) :
\(\displaystyle A(t) = 24,480 - \frac{66,096,000}{32,401} \cos(t) + \frac{367,200}{32,401} \sin(t) + C e^{-t/180}\)
The tank starts with A(0) = 15 oz of salt; use this to solve for the constant C.
\(\displaystyle 15 = 24,480 - \frac{66,096,000}{32,401} + C \implies C = -\dfrac{726,594,465}{32,401}\)
So,
\(\displaystyle A(t) = 24,480 - \frac{66,096,000}{32,401} \cos(t) + \frac{367,200}{32,401} \sin(t) - \frac{726,594,465}{32,401} e^{-t/180}\)
Recall the angle-sum identity for cosine:
\(R \cos(x-\theta) = R \cos(\theta) \cos(x) + R \sin(\theta) \sin(x)\)
so that we can condense the trigonometric terms in A(t). Solve for R and θ :
\(R \cos(\theta) = -\dfrac{66,096,000}{32,401}\)
\(R \sin(\theta) = \dfrac{367,200}{32,401}\)
Recall the Pythagorean identity and definition of tangent,
\(\cos^2(x) + \sin^2(x) = 1\)
\(\tan(x) = \dfrac{\sin(x)}{\cos(x)}\)
Then
\(R^2 \cos^2(\theta) + R^2 \sin^2(\theta) = R^2 = \dfrac{134,835,840,000}{32,401} \implies R = \dfrac{367,200}{\sqrt{32,401}}\)
and
\(\dfrac{R \sin(\theta)}{R \cos(\theta)} = \tan(\theta) = -\dfrac{367,200}{66,096,000} = -\dfrac1{180} \\\\ \implies \theta = -\tan^{-1}\left(\dfrac1{180}\right) = -\cot^{-1}(180)\)
so we can rewrite A(t) as
\(\displaystyle A(t) = 24,480 + \frac{367,200}{\sqrt{32,401}} \cos\left(t + \cot^{-1}(180)\right) - \frac{726,594,465}{32,401} e^{-t/180}\)
As t goes to infinity, the exponential term will converge to zero. Meanwhile the cosine term will oscillate between -1 and 1, so that A(t) will oscillate about the constant level of 24,480 oz between the extreme values of
\(24,480 - \dfrac{267,200}{\sqrt{32,401}} \approx 22,995.6 \,\mathrm{oz}\)
and
\(24,480 + \dfrac{267,200}{\sqrt{32,401}} \approx 25,964.4 \,\mathrm{oz}\)
which is to say, with amplitude
\(2 \times \dfrac{267,200}{\sqrt{32,401}} \approx \mathbf{2,968.84 \,oz}\)
Can someone please help me with this asap?

Answers
Answer: 3/5
Step-by-step explanation:
Convert 7/6 to a mixed number
Answers
Answer:
\( 1 \frac{1}{6} \)
Step-by-step explanation:
\(\huge \frac{7}{6} = 1 \frac{1}{6} \)
Hope it helps you in your learning process.
A tire manufacturer studying the effectiveness of television advertising and other promotions on sales of its GRIPPER-brand tires attempted to fit data it had gathered to the equation S = a_0 + a_1x + a_2x^2 + b_1y where S is sales revenue in millions of dollars, x is millions of dollars spent on television advertising, y is millions of dollars spent on other promotions, and a_0, a_1, a_2 and b_1 are constants. The data, gathered in two different regions of the country where expenditures for other promotions are kept constant (at B_1 and B_2), resulted in the following quadratic equations relations TV advertising and sales. Region 1: S_1 = 22 + 36x - 1.3x^2 + B_1 Region 2: S_2 = 38 + 19x - 0.6x^2 + B_2 The company wants to know how to make the best use of its advertising dollars in the regions and whether the current allocation could be improved. Advise management about current advertising effectiveness, allocation of additional expenditures, and reallocation of current advertising expenditures by answering the following questions.
1. In the analysis of sales and advertising, marginal return to sales is usually used, and it is given by ds/dx. Find the marginal return to sales for each region. If $10 million is being spent on TV advertising in each region, what is the marginal return to sales in each region?
2. Which region would benefit more from additional advertising expenditure, if $10 million is currently being spent in each region?
3. If any amount of additional money is made available for advertising, in which region should it be spent?
4. How could money already being spent be reallocated to produce more sales revenue
Answers
In order to advise the tire manufacturer on their advertising effectiveness and allocation, we need to calculate the marginal return to sales for each region, assess the impact of additional advertising expenditure, determine where the additional money should be spent, and consider the reallocation of current advertising expenditures.
To find the marginal return to sales for each region, we differentiate the sales equation with respect to x. For Region 1, ds_1/dx = 36 - 2.6x, and for Region 2, ds_2/dx = 19 - 1.2x. If $10 million is being spent on TV advertising in each region, we substitute x = 10 into the respective equations to find the marginal return to sales. In Region 1, ds_1/dx = 36 - 2.6(10) = 11, and in Region 2, ds_2/dx = 19 - 1.2(10) = 7. Hence, the marginal return to sales is $11 million in Region 1 and $7 million in Region 2.
To determine which region would benefit more from additional advertising expenditure, we compare the marginal returns. Since the marginal return in Region 1 is higher ($11 million) compared to Region 2 ($7 million), Region 1 would benefit more from additional advertising expenditure.
If additional money is made available for advertising, it should be spent in Region 1 as it has the higher marginal return. Increasing the advertising expenditure in Region 1 would likely result in a greater increase in sales revenue compared to Region 2.
To reallocate money already being spent to produce more sales revenue, we should compare the coefficients of the quadratic term (x^2) in the sales equations. In Region 1, the coefficient is -1.3, and in Region 2, it is -0.6. Since the coefficient in Region 1 is larger in absolute value, reallocating some advertising expenditure from Region 2 to Region 1 would likely lead to a larger increase in sales revenue overall.
Therefore, based on the analysis, the tire manufacturer should focus on increasing advertising expenditure in Region 1, as it has a higher marginal return, and consider reallocating some advertising funds from Region 2 to Region 1 to optimize sales revenue.
Learn more about marginal return here:
https://brainly.com/question/3116739
#SPJ11
Need Help here Please!

Answers
Answer:
Step-by-step explanation:

To solve the given equation \(\sf x - y = 4 \\\), we can perform the following calculations:
a) To find the value of \(\sf 3(x - y) \\\):
\(\sf 3(x - y) = 3 \cdot 4 = 12 \\\)
b) To find the value of \(\sf 6x - 6y \\\):
\(\sf 6x - 6y = 6(x - y) = 6 \cdot 4 = 24 \\\)
c) To find the value of \(\sf y - x \\\):
\(\sf y - x = - (x - y) = -4 \\\)
Therefore:
a) The value of \(\sf 3(x - y) \\\) is 12.
b) The value of \(\sf 6x - 6y \\\) is 24.
c) The value of \(\sf y - x \\\) is -4.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Use the double integral of a cross product to find the surface area of x = 2² + y that lies between the planes y=0.y=2, z=0, and z = 2.
Answers
The surface area of the given surface between the planes y = 0, y = 2, z = 0, and z = 2 is 4√2. The surface area of the given surface between the planes y = 0, y = 2, z = 0, and z = 2 is found using a double integral of a cross product.
To find the surface area, we'll use the double integral of a cross product formula: Surface Area = ∬√(1 + (fₓ)² + (fᵧ)²) dA
where fₓ and fᵧ are the partial derivatives of the function f(x, y) that defines the surface.
The given surface is defined by x = 2² + y. Let's find the partial derivatives of f(x, y): fₓ = ∂f/∂x = ∂/∂x (2² + y) = 0
fᵧ = ∂f/∂y = ∂/∂y (2² + y) = 1
Now, let's set up the double integral over the region between the planes y = 0, y = 2, z = 0, and z = 2:
Surface Area = ∬√(1 + (fₓ)² + (fᵧ)²) dA
Since fₓ = 0, the square root term becomes 1: Surface Area = ∬√(1 + (fᵧ)²) dA
The region of integration is defined by 0 ≤ y ≤ 2 and 0 ≤ z ≤ 2. We can express the surface area as a double integral:
Surface Area = ∫₀² ∫₀² √(1 + (fᵧ)²) dz dy
Since fᵧ = 1, the square root term simplifies:
Surface Area = ∫₀² ∫₀² √(1 + 1²) dz dy
= ∫₀² ∫₀² √2 dz dy
= √2 ∫₀² ∫₀² dz dy
= √2 ∫₀² [z]₀² dy
= √2 ∫₀² 2 dy
= √2 [2y]₀²
= √2 (2(2) - 2(0))
= 4√2
LEARN MORE ABOUT surface area here: brainly.com/question/29298005
#SPJ11
2. textbook authors and publishers work very hard to minimize the number of errors in a text. however, some errors are unavoidable. mr. j.a. carmen, statistics editor, reports that the mean number of errors per chapter is 3.0. what is the probability that there are less than two errors in a particular chapter? what is the probability that there are exactly two errors in a particular chapter?
Answers
The probability that there are less than two errors in a particular chapter and exactly two errors in a particular chapter is 0.1992 and 0.2240 respectively
We can model the number of errors in a chapter as a Poisson distribution with a mean of 3.0, since the occurrence of errors is random and independent, and the average number of errors is known.
Let X be the random variable representing the number of errors in a chapter.
To find the probability of less than two errors in a particular chapter, we need to calculate P(X < 2).
P(X < 2) = P(X = 0) + P(X = 1)
= e^(-3.0) × (3.0^0 / 0!) + e^(-3.0) × (3.0^1 / 1!)
= 0.0498 + 0.1494
= 0.1992
Therefore, the probability that there are less than two errors in a particular chapter is 0.1992 or approximately 19.92%.
To find the probability of exactly two errors in a particular chapter, we need to calculate P(X = 2).
P(X = 2) = e^(-3.0) × (3.0^2 / 2!)
= 0.2240
Therefore, the probability that there are exactly two errors in a particular chapter is 0.2240 or approximately 22.40%.
Learn more about probability here
brainly.com/question/11234923
#SPJ4