There are two cheesecakes in the fridge. The first cheesecake was cut into 10 slices and 4 slices were sold. How much cake is left in the fridge?
Answers
Answer: 1³/₅ of cake left
Step-by-step explanation:
There were two cheesecakes.
One was taken and cut into 10 slices, 4 of which were sold. The remainder of Cake A is:
= 10 - 4
= 6 slices
1 cake and 6 slices are therefore left.
As the 6 slices were originally 10, this expression in fraction is:
= 6/10
= 3/5
There are therefore:
= 1³/₅ of cake left
Related Questions
37 Previous Problem Problem List Next Problem (1 point) Consider the series, where n=1 (4n - 1)" an (2n + 2)2 In this problem you must attempt to use the Root Test to decide whether the series converges. Compute L = lim √lanl 818 Enter the numerical value of the limit L if it converges, INF if it diverges to infinity, MINF if it diverges to negative infinity, or DIV if it diverges but not to infinity or negative infinity. L = Which of the following statements is true?
A. The Root Test says that the series converges absolutely.
B. The Root Test says that the series diverges.
C. The Root Test says that the series converges conditionally.
D. The Root Test is inconclusive, but the series converges absolutely by another test or tests.
E. The Root Test is inconclusive, but the series diverges by another test or tests.
F. The Root Test is inconclusive, but the series converges conditionally by another test or tests.
Enter the letter for your choice here: 38 Previous Problem Problem List Next Problem (1 point) Match each of the following with the correct statement.
A. The series is absolutely convergent.
C. The series converges, but is not absolutely convergent.
D. The series diverges. (-2)" C 1. Σ=1 n² A 2. Σ1 (−1)n+1 (8+n)4″ (n²)42n sin(4n) D 3. Σ. 1 n5 (n+3)! C 4.-1 n!4" 8 5. Σ=1 D (-1)"+1 2n+4
Answers
Since the value of L is a finite positive number (2), we can conclude that the Root Test is inconclusive for this series.
To determine the convergence or divergence of the series using the Root Test, we compute the limit L = lim √(|an|) as n approaches infinity. For the given series Σ(4n - 1)/(2n + 2)^2, we evaluate L as follows:
L = lim √(|(4n - 1)/(2n + 2)^2|)
Taking the absolute value, we have:
L = lim √((4n - 1)/(2n + 2)^2)
Next, we simplify the expression under the square root:
L = lim √(4n - 1)/√((2n + 2)^2)
L = lim √(4n - 1)/(2n + 2)
Since both the numerator and denominator approach infinity as n increases, we apply the limit of their ratio:
L = lim (4n - 1)/(2n + 2)
By dividing the numerator and denominator by n, we get:
L = lim (4 - 1/n)/(2 + 2/n)
As n approaches infinity, both terms in the numerator and denominator become constants. Therefore, we have:
L = (4)/(2) = 2
Since the value of L is a finite positive number (2), we can conclude that the Root Test is inconclusive for this series. However, this does not provide information about the convergence or divergence of the series. Additional tests are needed to determine the nature of convergence or divergence.
To learn more about convergence click here, brainly.com/question/29258536
#SPJ11
Write an equation of the line that passes through (-2, 5) and (-4, -5)
Answers
Answer: 5x + 15 = y
Step-by-step explanation:
mx+b = y
find rise over run
(y_2-y_1)/(x_2-x_1) = m
(-5-5)/(-4+2)
simplify
-10/-2
10/2
5 = m
plug in a point and find b
5(-2) + b = 5
-10 + b = 5
b = 15
5x + 15 = y
Question 1
Researchers want to find a way to increase the growth rate of corn so it can be harvested more often. To test the effectiveness of a new type of spray fertilizer, plants grown from 200 corn seeds were divided equally into two groups: a treatment group and a control group. The treatment group was frequently sprayed with the new type of fertilizer. The growth in centimeters of each corn plant was noted before and after the treatment.
The results showed that the mean change in the growth rate by the treatment group is 8 points more than that of the control group. To test whether the results could be explained by random chance, researchers created a table that summarizes the results of 1,000 re-randomizations of the data with differences of means rounded to the nearest 2 points.
Consider the significance level to be set at 5%, so results less than 5% can be considered statistically significant.
Part B
Question
Which statement is true about the result considering a significance level of 5%?
The result is not statistically significant, which implies that spraying the corn plants with the new type of fertilizer does increase the growth rate.
The result is statistically significant, which implies that spraying the corn plants with the new type of fertilizer does increase the growth rate.
The result is statistically significant, which implies that spraying the corn plants with the new type of fertilizer does not increase the growth rate.
The result is not statistically significant, which implies that this result could be due to random chance.
Answers
Answer:
So what are you asking me to do
Answer:
A.
Step-by-step explanation:
Use the graph of function f(x)=x^3+x^2-5x+1 to identify the end-behavior, the number of turning points and the number of zeros
Answers
Solution:
Given:
\(f(x)=x^3+x^2-5x+1\)The graph of the function is given below;
The end behavior:
From the graph, the end behavior of the graph shows that as x tends to negative infinity, the function f(x) tends to negative infinity. Also, as x tends to positive infinity, the function f(x) tends to positive infinity.
\(\begin{gathered} x\rightarrow-\infty,f(x)\rightarrow-\infty \\ x\rightarrow\infty,f(x)\rightarrow\infty \end{gathered}\)The turning points:
The maximum number of turning points of a polynomial function is always one less than the degree of the function. A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising).
\(\begin{gathered} The\text{ degree of the function is 3} \\ The\text{ turning points will be }3-1=2 \end{gathered}\)The graph has a maximum and minimum point. Increasing and decreasing, and decreasing and increasing.
Hence, the graph of the function has two turning points.
The number of zeros:
The zeros of a function also referred to as roots or x-intercepts, occur at x-values where the value of the function f(x) = 0.
Hence, the zeros exist at;
\(x=-2.866,x=0.211,x=1.655\)Therefore, the function has three zeros.

Two functions f and g are defined on the set R of real numbers by f(x) = 2x - 1 and g(x) =x² + 1. Find the value of \(f^{-1}\)og (3)
Answers
Answer:
\(\frac{11}{2}\)
Step-by-step explanation:
To obtain the inverse of f(x)
let y = f(x) and rearrange making x the subject, that is
y = 2x - 1 ( add 1 to both sides )
y + 1 = 2x ( divide both sides by 2 )
\(\frac{y+1}{2}\) = x
Change y back into terms of x with x = \(f^{-1}\)(x) , thus
\(f^{-1}\)(x) = \(\frac{x+1}{2}\)
Evaluate g(3) and substitute the value obtained into \(f^{-1}\)(x)
g(3) = 3² + 1 = 9 + 1 = 10, then
\(f^{-1}\) (10) = \(\frac{10+1}{2}\) = \(\frac{11}{2}\)
What is the value of x in the equation 0.03x = 1.5?
Answers
Answer:
x = 50
Step-by-step explanation:
Divide each side by 0.03 to cancel out the 0.03 next to x. It should now look like this: x = 50I hope this helps!
Answer:
0.02
Step-by-step explanation:
Find the product:
[2 1 0] x [1 -1 2] = [a b c]
[-1 -2 1]
[0 1 1]
![Find the product:[2 1 0] x [1 -1 2] = [a b c] [-1 -2 1] [0 1 1]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/4Dbsnnbzg89QveTIRPvCydSETbTc2Jru.png)
Answers
Step-by-step explanation:
the multiplication result is found by row×column multiplications.
1st row × 1st column = a
2×1 + 1×-1 + 0×0 = 2 - 1 = 1 = a
1st row × 2nd column = b
2×-1 + 1×-2 + 0×1 = -2 + -2 = -4 = b
1st row × 3rd column = c
2×2 + 1×1 + 0×1 = 4 + 1 = 5 = c
2x - 3y = -5
5x - 22 = -4y
Solve In Multiplication Method
Answers
Answer:
(2, 3 )
Step-by-step explanation:
Given the 2 equations
2x - 3y = - 5 → (1)
5x + 4y = 22 → (2) [ rearranged equation ]
Multiplying (1) by 4 and (2) by 3 and adding will eliminate the term in y
8x - 12y = - 20 → (3)
15x + 12y = 66 → (4)
Add (3) and (4) term by term to eliminate y, that is
23x = 46 ( divide both sides by 23 )
x = 2
Substitute x = 2 in either of the 2 equations and evaluate for y
Substituting into (2)
5)2) + 4y = 22
10 + 4y = 22 ( subtract 10 from both sides )
4y = 12 ( divide both sides by 4 )
y = 3
Solution is (2, 3 )
1. One mole of an ideal gas expands isothermally at T = 20°C from 1.1 m³ to 1.8 m³. The gas constant is given by R = 8.314 J/(mol K). (a) Calculate the work done by the gas during the isothermal ex
Answers
The work done by the gas during the isothermal expansion is 331.32 J.
Isothermal Expansion refers to a process in which the temperature of a system stays constant while the volume increases. In this process, an ideal gas expands from 1.1 m³ to 1.8 m³, and the gas constant is R = 8.314 J/(mol K).
The work done by the gas during the isothermal expansion can be calculated as follows:Answer:During an isothermal process, the change in internal energy of the system is zero since the temperature remains constant.
Therefore,ΔU = 0The first law of thermodynamics is given by:ΔU = q + w
where q is the heat absorbed by the system, and w is the work done on the system.Since ΔU = 0 for an isothermal process, the above equation reduces to:w = -q
During an isothermal process, the heat absorbed by the system is given by the equation:q = nRTln(V₂/V₁)Where, n is the number of moles, R is the gas constant, T is the temperature, V₁ is the initial volume, and V₂ is the final volume.
Substituting the given values, we have:q = (1 mol) × (8.314 J/(mol K)) × (293 K) × ln(1.8 m³ / 1.1 m³)q = 331.32 J
Therefore, the work done by the gas during the isothermal expansion is given by:w = -qw = -(-331.32 J)w = 331.32 J
Thus, the work done by the gas during the isothermal expansion is 331.32 J.
Know more about Isothermal Expansion here,
https://brainly.com/question/30329152
#SPJ11
ayuda es para ahoritaaa
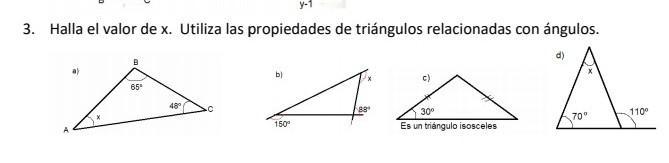
Answers
Answer:
a) 67
b) 122
c) que angulo
d) 40
Step-by-step explanation:
ind ∂w ∂v when u=0, v=0 if w=x2 y x, x=5u−5v 1, y=4u v−6.
Answers
The value of partial derivative ∂w/∂v when u=0, v=0 is 0.
To find ∂w/∂v when u=0, v=0, we can use the partial derivative formula:
∂w/∂v = (∂w/∂x) * (∂x/∂v) + (∂w/∂y) * (∂y/∂v)
First, let's find the partial derivatives of w with respect to x and y:
∂w/∂x = 2xy
∂w/∂y = x^2
Next, let's find the partial derivatives of x and y with respect to v:
∂x/∂v = 5(-1) = -5
∂y/∂v = 4u = 0 (since u=0)
Now we can plug in the values we have:
∂w/∂v = (2xy × ∂x/∂v) + (x^2 × ∂y/∂v)
At u=0, v=0, we have x=5u-5v=0 and y=4uv-6=0. Plugging in these values gives:
∂w/∂v = (2(0)(0)× -5) + ((0)^2×0) = 0
Click the below link, to learn more about the partial derivative formula:
https://brainly.com/question/30560681
#SPJ11
what are the steps to 3(x-4)-4x+5
Answers
Use distributive property
3x-12-4x+5
Simplify like terms
-1x-7
Answer can be
-x-7 or -1x-7 you can choose either one they are both correct i prefer -x-7
Select the correct answer. If A= and Ab= what is the value of matrix b

Answers
Answer: C. \(B=\left[\begin{array}{ccc}1\\3\\-5\end{array}\right]\)
Step-by-step explanation: I got this right on Edmentum.
Several operations such as addition, subtraction, multiplication, etc. can be performed on matrices. The value of matrix B is:
\(B =\left[\begin{array}{c}1&3&-5\end{array}\right]\)
Given that:
\(A =\left[\begin{array}{ccc}2&4&-2\\4&-5&7\\2&7&5\end{array}\right]\)
\(AB =\left[\begin{array}{c}24&-46&-2\end{array}\right]\)
Let matrix B be:
\(B =\left[\begin{array}{c}a&b&c\end{array}\right]\)
The product of A and B is as follows:
\(\left[\begin{array}{ccc}2&4&-2\\4&-5&7\\2&7&5\end{array}\right] \times\left[\begin{array}{c}a&b&c\end{array}\right]\)
Multiply the rows of A to the column of B. So, we have:
\(AB =\left[\begin{array}{ccc}2a+4b-2c\\4a-5b+7c\\2a+7b+5c\end{array}\right]\)
This means that:
\(\left[\begin{array}{ccc}2a+4b-2c\\4a-5b+7c\\2a+7b+5c\end{array}\right] = \left[\begin{array}{c}24&-46&-2\end{array}\right]\)
By comparison, we have:
\(2a + 4b - 2c = 24\) --- (1)
\(4a - 5b + 7c = -46\) --- (2)
\(2a + 7b + 5c = -2\) --- (3)
Multiply (1) and (3) by 2
\(2a + 4b - 2c = 24\) --- (1)
\(4a + 8b - 4c = 48\) ----- (5)
\(2a + 7b + 5c = -2\) --- (3)
\(4a + 14b + 10c = -4\) ---- (6)
So, we have:
\(4a - 5b + 7c = -46\) --- (2)
\(4a + 8b - 4c = 48\) ----- (5)
\(4a + 14b + 10c = -4\) ---- (6)
Make 4a the subject in each of the equations
\(4a = -46 + 5b - 7c\)
\(4a = 48 - 8b + 4c\)
\(4a = -4 - 14b - 10c\)
\(4a = 4a\). So, we have:
\(-46 + 5b - 7c = 48 - 8b + 4c\) and \(-46 + 5b - 7c = -4 - 14b - 10c\)
Simplify both expressions
\(-46 + 5b - 7c = 48 - 8b + 4c\)
\(5b + 8b - 7c - 4c = 48 + 46\)
\(13b - 11c = 94\)
\(-46 + 5b - 7c = -4 - 14b - 10c\)
\(5b+14b - 7c + 10c = 46-4\)
\(19b + 3c = 42\)
Make c the subject
\(c = \frac{42 -19b}{3}\)
Substitute \(c = \frac{42 -19b}{3}\) in \(13b - 11c = 94\)
\(13b - 11 \times (\frac{42 - 19b}{3}) = 94\)
Multiply through by 3
\(39b - 11 \times (42 - 19b) = 282\)
Open bracket
\(39b - 462 + 209b = 282\)
Collect like terms
\(39b + 209b = 282+462\)
\(248b = 744\)
Solve for b
\(b = \frac{744}{248}\)
\(b = 3\)
Solve for c
\(c = \frac{42 -19b}{3}\)
\(c = \frac{42 - 19 \times 3}{3}\)
\(c = \frac{-15}{3}\)
\(c = -5\)
Solve for a in \(4a = -4 - 14b - 10c\)
\(4a = -4 - 14 \times 3 - 10 \times -5\)
\(4a = 4\)
Divide by 4
\(a = 1\)
Recall that matrix B is:
\(B =\left[\begin{array}{c}a&b&c\end{array}\right]\)
Hence, the value of matrix B is:
\(B =\left[\begin{array}{c}1&3&-5\end{array}\right]\)
Read more on matrix operations at:
https://brainly.com/question/16956653
If the walls of a square room require 480 ft^2 of paint and the floor to ceiling height is 10
ft, what are the dimensions of the room?
Answers
Answer:
48 by 10 because
\(480\div 10 = 48\)
therefore the wall dimensions are 48 by 10
Consider the ordered bases B = {1, x, x2} and C = {1, (x - 1), (x - 1)2} for P2. (a) Find the transition matrix from C to B. (b) Find the transition matrix from B to C. (c) Write p(x) =
Answers
a. the matrix:
| a0 b0 c0 |
| a1 b1 c1 |
| a2 b2 c2 |
b. the matrix:
| p0 q0 r0 |
| p1 q1 r1 |
| p2 q2 r2 |
To find the transition matrix from basis C to basis B, we need to express each vector in basis C as a linear combination of vectors in basis B and then write the coefficients in matrix form.
(a) Transition matrix from C to B:
To express each vector in C as a linear combination of vectors in B, we solve the following system of equations:
1 = a0 * 1 + a1 * x + a2 * x^2
(x - 1) = b0 * 1 + b1 * x + b2 * x^2
(x - 1)^2 = c0 * 1 + c1 * x + c2 * x^2
We solve this system of equations and find the coefficients a0, a1, a2, b0, b1, b2, c0, c1, c2. Then we form the matrix:
| a0 b0 c0 |
| a1 b1 c1 |
| a2 b2 c2 |
(b) Transition matrix from B to C:
To express each vector in B as a linear combination of vectors in C, we solve the following system of equations:
1 = p0 * 1 + p1 * (x - 1) + p2 * (x - 1)^2
x = q0 * 1 + q1 * (x - 1) + q2 * (x - 1)^2
x^2 = r0 * 1 + r1 * (x - 1) + r2 * (x - 1)^2
We solve this system of equations and find the coefficients p0, p1, p2, q0, q1, q2, r0, r1, r2. Then we form the matrix:
| p0 q0 r0 |
| p1 q1 r1 |
| p2 q2 r2 |
(c) To complete part (c), please provide the polynomial p(x) that you want to write in terms of the basis C or B.
Learn more about matrix here
https://brainly.com/question/30389982
#SPJ11
When you spin a rectangle, what 3D figure do you get? cylinder prism cone sphere
Answers
Answer:
A cylinder
Step-by-step explanation:
When you rotate the rectangle you are make a circle but since its volume the original height of the rectangle is the height of the circle which would mean a cylinder.

Answer:
CYLINDER
Step-by-step explanation:
Oliver uses 30 fruits to make a large batch of pineapple-orange juice. He uses 5 oranges for every 1 pineapple. He gets 2.5 fl oz of juice from each orange and 20 fl oz of juice from each pineapple
Answers
Answer:
isnt like 40 the answer (im sorry if im wrong 3rd grader)
Step-by-step explanation:
Simplify: \(x^{2}\) - xy + yx - \(y^{2}\)
Answers
Please find attached photograph for your answer. Don't forget to mark me Brainliest if you like my answer
![Simplify: [tex]x^{2}[/tex] - xy + yx - [tex]y^{2}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/oyVLW2zNdVDGYDoSWFx3ufnqZ53DD9NL.jpeg)
a point moves in a plane such that its position is defined by x = ln2t and y = 3 − t^3. find the acceleration vector when t = 2.√2305/16√325/4[-1/4, -12][-1/2,-12]
Answers
The acceleration vector when t = 2, is (-1/4, -12).
option B.
What is the acceleration vector?
The acceleration vector of the point is calculated as follows;
The position vector of the point at time t = y r(t) = (x(t), y(t)) = (ln(2t), 3 - t³).
The velocity vector is calculated as follows;
v(t) = r'(t)
v(t) = (dx/dt, dy/dt)
v(t) = (d/dt(ln(2t)), d/dt(3 - t³))
v(t) = (1/t, -3t²)
Acceleration is change in velocity with time, so the acceleration vector is calculated as follows;
a(t) = v'(t) = (d/dt(1/t), d/dt(-3t²))
a(t) = (-1/t², -6t)
The acceleration vector when t = 2, is calculated as follows;
a(2) = (-1/2², -6(2) )
a(2) = (-1/4, -12)
Learn more about acceleration vector here: https://brainly.com/question/31134791
#SPJ1
5 points
4. Some banks charge a fee on savings accounts that are left inactive for
an extended period of time. The equation y = 5000(0.98)x represents the
value, y, of one account that was left inactive for a period of x years. What
is the y-intercept of this equation and what does it represent? *
Answers
Answer:
(0, 5000)
The value of the account at the start of the year is 5000
Step-by-step explanation:
Given the equation that represents the value, y, of one account that was left inactive for a period of x years as;
y = 5000(0.98)^x
The y-intercept of the equation occurs at x = 0
Substitute x = 0 into the expression
y = 5000(0.98)^0
y = 5000(1) (any value raise to power of zero is 1)
y = 5000
Hence the y intercept is (0, 5000)
This means that the value of the account at the start of the year is 5000
Which statement is true about the number −5? The number −5 is not a rational number because it cannot be written as a ratio of integers. The number −5 is not rational number because it is a negative integer. The number −5 is a rational number because it can be written as the fraction −51. The number −5 is a rational number because it can be written as the fraction −50.
Answers
Answer:
The number -5 is not a rational number because it is a negative integers.
Step-by-step explanation:
Hopes This Helps :)
B is between A and C, AC = 14 and BC = 11.4. Find AB
Answers
Answer: 2.6
Step-by-step explanation:
1. We know that A to C is 14
2. B to C is 11.4 so we're going to find the remainder to equal 14.
3. 14 minus11.4 which equals 2.6
4. AB is 2.6
Find P(A∣E) and P(C∣F) using the tree diagram below. (Round your answers to four decimal places.) P(A∣E) P(C∣F)
Answers
So, P(C|F) is approximately equal to 0.6667, rounded to four decimal places.
To find P(A|E) and P(C|F) using the tree diagram, we need to determine the conditional probabilities.
Looking at the tree diagram, we can see that the event E occurs in two out of the four branches, and the event A occurs in one of those branches. Therefore, we can calculate P(A|E) as follows:
P(A|E) = P(A ∩ E) / P(E)
From the tree diagram, we see that P(A ∩ E) is the probability of the branch that leads to both A and E, which is 0.15.
To calculate P(E), we sum up the probabilities of the branches that lead to E, which are 0.15 and 0.05.
P(E) = 0.15 + 0.05 = 0.20
Now we can calculate P(A|E):
P(A|E) = P(A ∩ E) / P(E) = 0.15 / 0.20 = 0.7500
So, P(A|E) is equal to 0.7500.
Similarly, we can calculate P(C|F) using the same approach:
P(C|F) = P(C ∩ F) / P(F)
From the tree diagram, we see that P(C ∩ F) is the probability of the branch that leads to both C and F, which is 0.20.
To calculate P(F), we sum up the probabilities of the branches that lead to F, which are 0.10 and 0.20.
P(F) = 0.10 + 0.20 = 0.30
Now we can calculate P(C|F):
P(C|F) = P(C ∩ F) / P(F) = 0.20 / 0.30 = 0.6667
So, P(C|F) is approximately equal to 0.6667, rounded to four decimal places.
Learn more about decimal here:
https://brainly.com/question/28393353
#SPJ11
Hellohello, if you able to help me then please do. (:

Answers
Answer:
The answer is D.
Sum means addition. So, you would be adding a and b. Remember this; a - b = difference, a * b = product, a ÷ b = quotient, and a + b = sum. Good luck!
Answer:
d) a+b
Step-by-step explanation:
For this question we can think of a and b as different numbers just for the sake of making the question easier. For example "a" could be 2 and "b" could be 3 (a=2 and b=3).
(However, keep in mind that "a" and "b" can be any number and that we don't know their values. But we can assign some values to them in order to solve the question more easily)
So if a=2 and b=3 in our example the notation for their sum would be 2+3. If we just put a for 2 and b for 3 we get a+b, which is the answer
the given set is a basis for a subspace w. use the gram-schmidt process to produce an orthogonal basis for w.
Answers
y₁ = [1 -4 0 1] and y₂ = [5 1 -6 -1] is the orthogonal basis for w using Gram-Schmidt process.
Given,
The set;
x₁ = [1 -4 0 1]
x₂ = [7 -7 -6 1]
We have to produce the orthogonal basis for w using the Gram-Schmidt process;
Here,
y₁ = x₁ = [1 -4 0 1]
Now,
Solve for y₂
y₂ = x₂ - [x₂y₁ / y₁y₁] y₁
That is,
y₂ = [7 -7 -6 1] - ( [7 -7 -6 1] [1 -4 0 1] / [1 -4 0 1] [1 -4 0 1] ) × [1 -4 0 1]
y₂ = [7 -7 -6 1] - (7 + 28 - 0 + 1) / (1 + 16 + 0 + 1) × [1 -4 0 1]
y₂ = [7 -7 -6 1] - 36/18 × [1 -4 0 1]
y₂ = [7 -7 -6 1] - 2 × [1 -4 0 1]
y₂ = [7 -7 -6 1] - [2 8 0 2]
y₂ = [5 1 -6 -1]
That is,
The orthogonal basis for w using Gram-Schmidt process is,
y₁ = [1 -4 0 1] and y₂ = [5 1 -6 -1]
Learn more about Gram-Schmidt process here;
https://brainly.com/question/17132977
#SPJ4
Find the slope of each line in the figure.
Slope of p =
Slope of q =
Slope of r =
Slope of m =
Slope of n =

Answers
Answer:
slope of p= -7/12
slope of q= -3/6.8
slope of r= -16/6.4
slope of m= 6.2/15.5
slope of n= 6.8/17
Step-by-step explanation:
The slopes of the line are given as 2.5 for p and q and -2.5 for r, m and n respectively.
What is the slope of straight line?The slope of a straight line is the tangent of the angle formed by it with the positive x axis as the reference.
The negative slope indicates the rate of decrease while the positive shows the rate of increase.
The slope of the given lines can be obtained as follows,
(a) In order to find slope of line p,
Use the formula m = (x₂ - x₁)/(y₂ - y₁) and substitute the corresponding values to get,
m = (-3 - 8)/(0.4 - (-4))
⇒ m = -2.5
(b) In order to find slope of line q,
Use the formula m = (x₂ - x₁)/(y₂ - y₁) and substitute the corresponding values to get,
m = (13 - 0)/(6.8 - 12)
⇒ m = -2.5
(c) In order to find slope of line r,
Use the formula m = (x₂ - x₁)/(y₂ - y₁) and substitute the corresponding values to get,
m = (13 - (-3))/(6.8 - 0.4)
⇒ m = 2.5
(d) In order to find slope of line m,
Use the formula m = (x₂ - x₁)/(y₂ - y₁) and substitute the corresponding values to get,
m = (-15.5 - 0)/(0 - 6.2)
⇒ m = 2.5
(e) In order to find slope of line n,
Use the formula m = (x₂ - x₁)/(y₂ - y₁) and substitute the corresponding values to get,
m = (-5 - 12)/(- 6.8 - 0)
⇒ m = 2.5
Hence, the slopes of first two lines are 2.5 and of the remaining three are 2.5.
To know more about slope click on,
https://brainly.com/question/3605446
#SPJ2
1. what is 0.7 of 42
2. what is 0.3 of 14
Answers
Answer:1) 29.4
2)4.2
Step-by-step explanation:
0.7×42=29.4
0.3×14=4.2
use the given data to answer the question. what is the critical value for the f- test at 95% confidence? df ss ms f p
Answers
To determine the critical value for the F-test at 95% confidence, we need the degrees of freedom for the numerator (df) and the denominator (df), along with the significance level (α) to find the critical value from an F-distribution table.
The F-test is used to compare the variances of two populations. In this case, we need additional information such as the sum of squares (SS), mean squares (MS), and the p-value to calculate the critical value for the F-test accurately.
Without the values for df, SS, MS, F, and p, it is not possible to provide a specific calculation for the critical value at 95% confidence.
The critical value for the F-test at 95% confidence depends on the degrees of freedom, sum of squares, mean squares, F-statistic, and p-value. To determine the specific critical value, these values are required. Without the given data, it is not possible to provide an exact answer.
To know more about numerator , Visit:
https://brainly.com/question/1217611
#SPJ11
Easy i just want confirmation What is 3 to the power of three halves equal to?
- cube root of 9
- square root of 9
- cube root of 27
- square root of 27
Answers
The 3 to the power of three halves equal to square root of 27 sqrt(27).
What is the square root?
A square root of a number x is a number y such that y² = x; in other words, a number y whose square is x. For example, 4 and −4 are square roots of 16, because 4² = ² = 16.
A square root is a number that can be multiplied by itself to give the original number.
3 to the power of 3/2 is equal to the square root of 3 to the power of 3, which is equal to the square root of 27. The square root of 27 is approximately 3.872983346207417.
To calculate this value, you can use a calculator or you can use the following formula:
3^(3/2) = sqrt(3^3) = sqrt(27) = 3.872983346207417
Hence, the 3 to the power of three halves equal to square root of 27 sqrt(27).
To learn more about the square root visit,
https://brainly.com/question/428672
#SPJ1
the equation y=12.7x+15.2 estimates the amount that businesses will spend, in billions of dollars, on internet software to conduct transactions via the web, where x is the number of years after 2002. for what years will the spending be more than $66 billion?
Answers
The years when the spending be more than $66 billion is in 4 years time.
What is an equation?A mathematical equation is the statement that illustrates that the variables given. In this case, two or more components are taken into consideration to describe the scenario.
The equation is given as y=12.7x+15.2 and the amount is $66 billion. Therefore, the value of x will be:
y=12.7x+15.2
66 = 12.7x + 15.2
Collect like terms
12.7x = 66 - 15.2
12.7x = 50.8
Divide
x = 50.8 / 12.7
x = 4
The number of years is 4.
Learn more about equations on:
brainly.com/question/2972832
#SPJ1