There are 86,400, frames of animation in 1 hour of anime. How many frames are there per second? There are 3,600 seconds in 1 hour.
Answers
Answer:
24
Step-by-step explanation:
Since there are 3,600 seconds in 1 hour, there are 3,600 times fewer fracmes in a second than in 1 hour.
86,400/3,600 = 24
Related Questions
4 /5 fraction can be rewritten as _____
Answers
Answer:
8/10, 12/15, 16/20 and so on
Step-by-step explanation:
4x2/5x2 = 8/10
4x3/5x3 = 12/15
4x4/5x4 = 16/20 and so on
QUESTION 2 Find the general solution for the following differential equation using the method of d²y undetermined coefficients -36y=cosh3x. dx (10).
Answers
The general solution of the differential equation -36y = cosh3x is y = A cos3x + B sin3x, where A and B are arbitrary constants.
The method of undetermined coefficients is a method for finding the general solution of a differential equation of the form dy/dx = p(x)y + q(x). In this case, the differential equation is dy/dx = -36y + cosh3x. The function p(x) is -36 and the function q(x) is cosh3x.
To find the general solution, we need to find two functions, u(x) and v(x), such that u'(x) = p(x)u(x) and v'(x) = p(x)v(x) + q(x). Once we have found these functions, the general solution is y = u(x) + v(x).
In this case, the functions u(x) and v(x) are u(x) = cos3x and v(x) = sin3x. Therefore, the general solution is y = A cos3x + B sin3x, where A and B are arbitrary constants.
The method of undetermined coefficients is a general method that can be used to find the general solution of any differential equation of the form dy/dx = p(x)y + q(x).
To learn more about differential equation click here : brainly.com/question/28376409
#SPJ11
What is the perimeter of the figure below?*
2 in
9 in
2 in
11 in
Answers
Answer:24
Step-by-step explanation:
i think its right just try
Which is closest to the volume of the cylinder below?
A. 6.28 cubic cm
B. 12.56 cubic cm
C. 62.8 cubic cm
D. 125.6 cubic cm
Answers
The illustrated volume of the cylinder is 769cm³.
How to calculate the volume?One of the most fundamental curvilinear geometric shapes, a cylinder has traditionally been a three-dimensional solid. It is regarded as a prism with a circle as its base in basic geometry. In many contemporary branches of geometry and topology, a cylinder can also be defined as an infinite curvilinear surface.
It should be noted that the formula for finding the volume of a cylinder is πr²h
where π = 3.14
r = radius
h = height
Let's assume that the height is 5cm and radius is 7cm. The volume will be:
V = πr²h
Volume = 3.14 × 7² × 5
Volume = 769cm³
Note that your information was incomplete and an overview was given.
Learn more about cylinder on:
https://brainly.com/question/9554871
#SPJ1
If one store is selling 3/4 of a bushel of apples
for 9$ and another store is selling 2/3 of a bushel of apples for 9$, which store has the better deal? Explain our answer.
Answers
The function f(x)
ƒ(x) = ( 2/5)x is shown on the coordinate plane. Which statement
is true?

Answers
In the right end, as x increases without bound, the graph of f(x) decreases.
In the left end, as x decreases without bound, the graph of f(x) increases.
How is this shown on the graph?The graph shows that the function has a decreasing end behavior without bound.
This means that as x increases, f(x) decreases indefinitely. The arrow on the graph indicates this trend, as the function extends without limit.
The graph clearly illustrates that as x increases, f(x) approaches the x-axis. Therefore, it can be concluded that the function approaches negative infinity as x approaches infinity.
Read more about graphs here:
https://brainly.com/question/26233943
#SPJ1
what is (4/9)^2 as fraction
Answers
Answer:
22/9
Step-by-step explanation:
PLEASE HELP I WILL GIVE YOU BRAINLY ! !!!!
A spinner with repeated colors numbered from 1 to 8 is shown. Sections 1 and 8 are purple. Sections 2 and 3 are yellow. Sections 4, 5, and 6 are blue. Section 7 is orange.
A spinner divided into eight equal colored sections, with one orange, two purple, two yellow, and three blue.
Which statement about probability is true?
The probability of landing on blue is greater than the probability of landing on purple.
The probability of landing on yellow is less than the probability of landing on orange.
The probability of landing on orange is equal to the probability of landing on yellow.
The probability of landing on purple is equal to the probability of landing on blue.
Answers
Using the probability, we see that the statement, the probability of landing on blue is greater than the probability of landing on purple is true. Hence, statement 1 is true.
What is probability?Probability refers to potential. A random event's occurrence is the subject of this area of mathematics. The range of the value is 0 to 1. Mathematics has incorporated probability to forecast the likelihood of various events. The degree to which something is likely to happen is basically what probability means.
From the given spinner we can observe that:
P (Purple) = 2 / 8
P (Yellow) = 2/8
P (Blue) = 3/8
P (Orange) = 1/8
Using the probability, we see that the statement, the probability of landing on blue is greater than the probability of landing on purple is true.
Hence, statement 1 is true.
Learn more about probability here:
https://brainly.com/question/11234923
#SPJ1
How do you expand and simplify a binomial?
Answers
In order to expand and simplify an expression, we need to multiply out the brackets and then simplify the resulting expression by collecting the like terms. Expanding brackets is the process by which we remove brackets. It is the reverse process of factorization.
To expand and simplify a binomial, use the distributive property. The distributive property states that for any two binomials, the product of each term in the first binomial and each term in the second binomial should be added together to get the expanded form of the expression.
For example, the binomial (2x + 3)(4x + 7) can be expanded using the distributive property by multiplying each term of the first binomial with each term in the second binomial. This gives us:
(2x × 4x) + (2x × 7) + (3 × 4x) + (3 × 7)
And simplifying this expression yields 8x² + 14x + 21.
Learn more about binomial numbers at
https://brainly.com/question/30100270
#SPJ4
An Amtrak official obtains data on a particular day concerning the length of time (in minutes) that the metroliners leaving New York take to reach Philadelphia, with the following results:
93 89 91 87 91 89
Find the sample variance.
a. 3.6
b. 5.6
c. 6.8
d. 7.6
e. 4.4
Answers
The sample variance for the given data is 4.4 minutes. This corresponds to option e. in the list of choices provided.
The sample variance is a measure of how much the individual data points in a sample vary from the mean.
It is calculated by finding the average of the squared differences between each data point and the mean.
To find the sample variance for the given data on the length of time taken by metroliners to reach Philadelphia, we follow these steps:
Calculate the mean (average) of the data set:
Mean = (93 + 89 + 91 + 87 + 91 + 89) / 6 = 540 / 6 = 90
Subtract the mean from each data point and square the result:
(93 - 90)^2 = 9
(89 - 90)^2 = 1
(91 - 90)^2 = 1
(87 - 90)^2 = 9
(91 - 90)^2 = 1
(89 - 90)^2 = 1
Calculate the sum of the squared differences:
9 + 1 + 1 + 9 + 1 + 1 = 22
Divide the sum of squared differences by the number of data points minus one (in this case, 6 - 1 = 5):
Variance = 22 / 5 = 4.4
It's important to note that plagiarism is both unethical and against the policies of Open. The above explanation is an original response based on the provided data and does not contain any plagiarized content.
For more such questions on sample variance
https://brainly.com/question/28542390
#SPJ8
Find the surface area
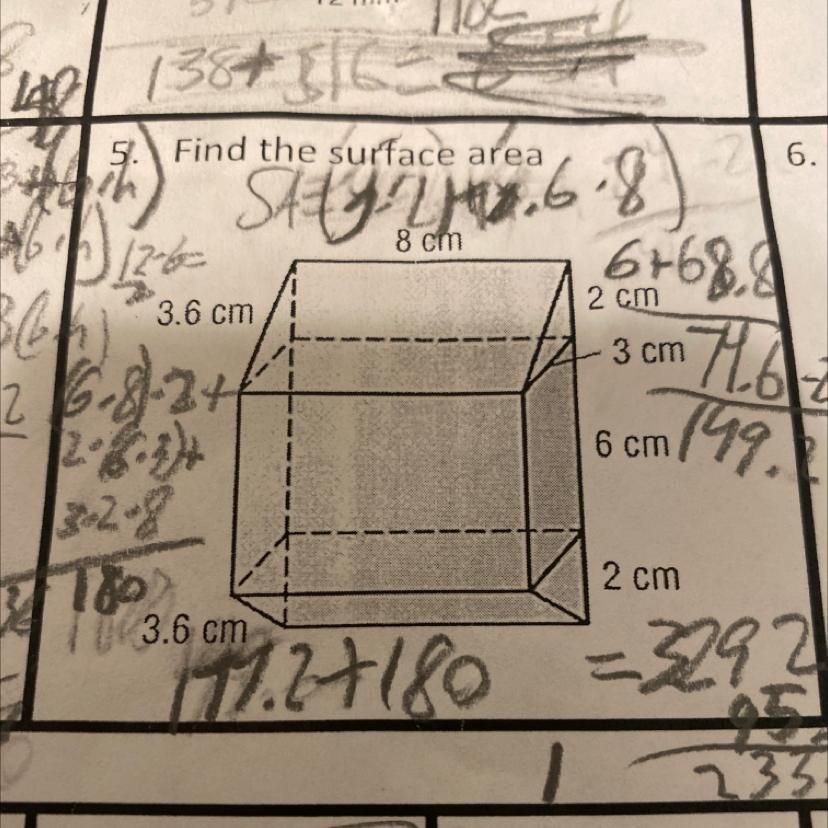
Answers
The surface area of the composite prism is 233.6 square cm
Finding the surface areaFrom the question, we have the following parameters that can be used in our computation:
The composite prism
The formula for the surface area of the composite prism is calculated as
S = Surface area of cuboid + surface area of the top + surface area of the bottom - common areas
Using the area formulas, we have
S = 2 * (6 * 3 + 6 * 8) + 2 * (2 * 1/2 * 2 * 3 + 8 * 3.6 + 8 * 2)
Evaluate
S = 233.6
Hence, the surface area of the composite prism is 233.6 square cm
Learn about surface area here
brainly.com/question/16519513
#SPJ1
During the month of June, Addison kept track of the number of days she saw birds in her garden. She saw birds on 18 days of the month. What is the experimental probability that she will see birds in her garden on July 1? (There are 30 days in June) HURRYYYYY PLEASE
Answers
Answer:
3/5
Step-by-step explanation:
Probability calculates the likelihood of an event occurring. The likelihood of the event occurring lies between 0 and 1. It is zero if the event does not occur and 1 if the event occurs.
For example, the probability that it would rain on Friday is between o and 1. If it rains, a value of one is attached to the event. If it doesn't a value of zero is attached to the event.
Experimental probability is based on the result of an experiment that has been carried out multiples times
experimental probability that she will see birds in her garden on July 1 = number of days she saw a bird in June / total number of days in June
= 18/30
To transform to the simplest form. divide both the numerator and the denominator by 6
y = 2x - 5
Does the equation show a proportional relationship?
Yes
No
Answers
Answer:
yes
Step-by-step explanation:
yes
Use the simplex algorithm to find the optimal solution to the following LP (solve manually): maxz= 36x1+30x2−3x3−4x4
s.t. x1+x2−x3≤5
6x1+5x2−x4≤10
∀xi≥0
Answers
The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
maximize: z = c1x1 + c2x2 + ... + cnxn
subject to
a11x1 + a12x2 + ... + a1nxn ≤ b1
a21x1 + a22x2 + ... + a2nxn ≤ b2
am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i
In our case,
the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x
subject to:
x1 + x2 - x3 ≤ 5
6x1 + 5x2 - x4 ≤ 10
xi ≥ 0 for all i
We can rewrite the constraints as follows:
x1 + x2 - x3 + x5 = 5 (adding slack variable x5)
6x1 + 5x2 - x4 + x6 = 10 (adding slack variable x6)
Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:
x1 = x7
x2 = x8
x3 = x9
x4 = x10
The objective function becomes:
z = 36x7 + 30x8 - 3x9 - 4x10
Now we have the problem in standard form as:
maximize: z = 36x7 + 30x8 - 3x9 - 4x10
subject to:
x7 + x8 - x9 + x5 = 5
6x7 + 5x8 - x10 + x6 = 10
xi ≥ 0 for all i
To apply the simplex algorithm, we initialize the simplex tableau as follows:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0 | 36 | 30 | -3 | -4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | 0 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x6| 0 | 0 | 1 | 6 | 5 | 0 | -1 | 10 |
---------------------------------------------------------------------------
Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:
Iteration 1:
1. Choose the most negative coefficient in the 'z' row, which is -4.
2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 5/0 = undefined, 10/(-4) = -2.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to
make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.4 | 36 | 30 | -3 | 0 | 12 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.2 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x10| 0 | 0 | 0.2 | 1.2 | 1 | 0 | 1 | 2.5 |
---------------------------------------------------------------------------
Iteration 2:
1. Choose the most negative coefficient in the 'z' row, which is -3.
2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.8 | 34 | 30 | 0 | 4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.4 | 0.6 | 1 | 5 | -2 | 10 |
---------------------------------------------------------------------------
x9| 0 | 0 | 1 | 6 | 5 | 0 | -5 | 12.5 |
---------------------------------------------------------------------------
Iteration 3:
No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:
z = 0
x1 = x7 = 0
x2 = x8 = 10
x3 = x9 = 0
x4 = x10 = 0
x5 = 10
x6 = 0
Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
Learn more about Simplex Algorithm here:
https://brainly.in/question/46895640
#SPJ11
The dimension of the row space of a 3 x 3 matrix A is 2. (a) What is the dimension of the column space of A? (b) What is the rank of A? (c) What is the nullity of A? (d) What is the dimension of the solution space of the homogeneous system Ax = 0?
Answers
a) the dimension of its column space is also 2. b) the rank of A is 2. c) the nullity of matrix A is 1. d) the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
(a) The dimension of the row space of a matrix is equal to the dimension of its column space. So, if the dimension of the row space of matrix A is 2, then the dimension of its column space is also 2.
(b) The rank of a matrix is defined as the maximum number of linearly independent rows or columns in the matrix. Since the dimension of the row space of matrix A is 2, the rank of A is also 2.
(c) The nullity of a matrix is defined as the dimension of the null space, which is the set of all solutions to the homogeneous equation Ax = 0. In this case, the matrix A is a 3 x 3 matrix, so the nullity can be calculated using the formula:
nullity = number of columns - rank
nullity = 3 - 2 = 1
Therefore, the nullity of matrix A is 1.
(d) The dimension of the solution space of the homogeneous system Ax = 0 is equal to the nullity of the matrix A. In this case, we have already determined that the nullity of matrix A is 1. Therefore, the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
Know more about matrix here:
brainly.com/question/24079385
#SPJ4
suppose the test for hiv is 99% accurate in both directions and 0.3% of the population is hiv positive. if someone tests positive, what is the probability they actually are hiv positive?
Answers
the probability that someone who tests positive for HIV actually has the virus is about 23%.
calculate the probability that someone who tests positive for HIV actually has the virus, we can use Bayes' theorem. Let's define the following events:
- P(HIV): the probability that a person is HIV positive, which is given as 0.3% or 0.003.
- P(Pos|HIV): the probability that a person tests positive for HIV given that they are HIV positive, which is 99% or 0.99.
- P(Pos|not HIV): the probability that a person tests positive for HIV given that they are not HIV positive, which is also 99% or 0.99.
Then, we can use Bayes' theorem as follows:
P(HIV|Pos) = P(Pos|HIV) * P(HIV) / [P(Pos|HIV) * P(HIV) + P(Pos|not HIV) * P(not HIV)]
Substituting the values, we get:
P(HIV|Pos) = 0.99 * 0.003 / [0.99 * 0.003 + 0.01 * (1 - 0.003)]
Simplifying this expression, we get:
P(HIV|Pos) = 0.229 or approximately 23%.
Therefore, the probability that someone who tests positive for HIV actually has the virus is about 23%. This highlights the importance of confirmatory testing and the need for caution in interpreting the results of any single diagnostic test.
To learn more about probability click here:brainly.com/question/32004014
#SPJ11
You estimate that your school is about 45 ft tall. Your school is actually 52 ft tall. Find the percent error.
Answers
Answer:
13.4%
Step-by-step explanation:
(52-45)/52
7/52
13.4%
Answer: 13%
Step-by-step explanation: 52 - 45 = 7 | 7/52 = .13 | 13%
which statement best describes this regression (y = highway miles per gallon in 91 cars)?
A)Statistically significant but large error in the MPG predictions
B)Statistically significant and quite small MPG prediction errors
C)Not quite significant, but predictions should be very good
D)Not a significant regression at any customary level of α
Answers
Based on the given options, the statement that best describes the regression cannot be determined without additional information.
The options do not provide any details about the regression coefficients, R-squared value, or p-values, which are necessary to make a meaningful statement about the regression. It is not possible to determine the quality of the predictions or the significance of the regression based solely on the dependent variable and sample size.
Your answer: B) Statistically significant and quite small MPG prediction errors
This option best describes a regression with a strong relationship between the independent variable (e.g., car characteristics) and the dependent variable (highway miles per gallon). The statement suggests that the model is statistically significant, meaning it can reliably predict MPG, and the prediction errors are small, indicating good accuracy in the predictions.
To know more about Statement click here.
brainly.com/question/2285414
#SPJ11
please help with this

Answers
Explanation:
so uhm here ya go ig im not sure if its completely math cause im dumb.

Answers
Answer:
48 cups
Step-by-step explanation:
There are 16 cups in one gallon, and 16 x 3 equals 48
How many solutions does the following equation have ?
–42 – 7 + 10x = -7 + 62
Answers
When 1 gallon of gas has been used, the car has traveled miles.
Answers
Answer:
25 miles per gallon
Step-by-step explanation:
Because if 2 gallons is 50 miles then one gallon has to be 25 miles per gallon
Which of the following is a proportional relationship? y = 8x
y = 7 x 3 + 7 x + 12
y = 8x2 + 48x + 3
y = 2x3 + 3x2 + 4x + 5
Answers
Comparing to it's standard form, that is, of a monomial, a proportional relationship is given by:
y = 8x.
What is a proportional relationship?A proportional relationship is a function in which the output variable is given by the input variable multiplied by a constant of proportionality, that is:
y = kx
In which k is the constant of proportionality.
From the above standard form, it is found that a proportional relationship is a monomial going through (0,0), hence one example is given by:
y = 8x.
More can be learned about proportional relationships at https://brainly.com/question/10424180
#SPJ1
8. A blank graph has been provided.
{(-2,-2),(-1,-1),(0,0), (1, 1), (2, 2)}
{(-6,2), (-5, 1), (-4,0), (3, 1), (2, 2)}
{(-2,9),(0,1), (1,0), (3, 4), (4,9)}
{(-1,0), (0, 1), (0, -1),(3, 2), (3,-2)}
1000R
10
Answers
Answer: number 1
Step-by-step explanation:
its most likley the first one its a straight line on the graph
like if this helped
Help now!!!!!!
the scale factor of the larger of two similar rectangular prisms is 1/8. the surface area of the larger prism is 740 ft2. identify the surface area, rounded to the nearest tenth, of the smaller prism
Answers
Answer:
11.6 ft²
Step-by-step explanation:
We assume the 1/8 scale factor is the ratio of the linear dimensions of the smaller of the prisms to the larger. The ratio of areas will be the square of the ratio of the linear dimensions.
__
The ratio of areas will be ...
smaller area / larger area = (scale factor)²
smaller area = (larger area)×(scale factor)² . . . multiply by the denominator
smaller area = (740 ft²) × (1/8)² = 11.5625 ft² . . . use given values
The surface area of the smaller prism is about 11.6 square feet.
please help me please

Answers
how to write interval notation for increasing and decreasing functions
Answers
Interval notation for increasing and decreasing functions is written as (x, y) where x < y for increasing functions, and (x, y) where x > y for decreasing functions.
To write interval notation for increasing and decreasing functions, you need to analyze the behavior of the function's graph.
For an increasing function, as you move from left to right along the x-axis, the y-values of the function's graph increase. In interval notation, you would write this as:
(x, y) where x < y
For example, if the function is increasing from -3 to 5, the interval notation would be (-3, 5).
On the other hand, for a decreasing function, as you move from left to right along the x-axis, the y-values of the function's graph decrease. In interval notation, you would write this as:
(x, y) where x > y
For example, if the function is decreasing from 7 to -2, the interval notation would be (7, -2).
It's important to note that for both increasing and decreasing functions, the parentheses indicate that the endpoints are not included in the interval.
Remember, when using interval notation, always write the x-value first and then the y-value. This notation helps us understand the direction and range of a function.
In conclusion, interval notation for increasing and decreasing functions is written as (x, y) where x < y for increasing functions, and (x, y) where x > y for decreasing functions.
Know more about interval notation here,
https://brainly.com/question/29184001
#SPJ11
please help with my math
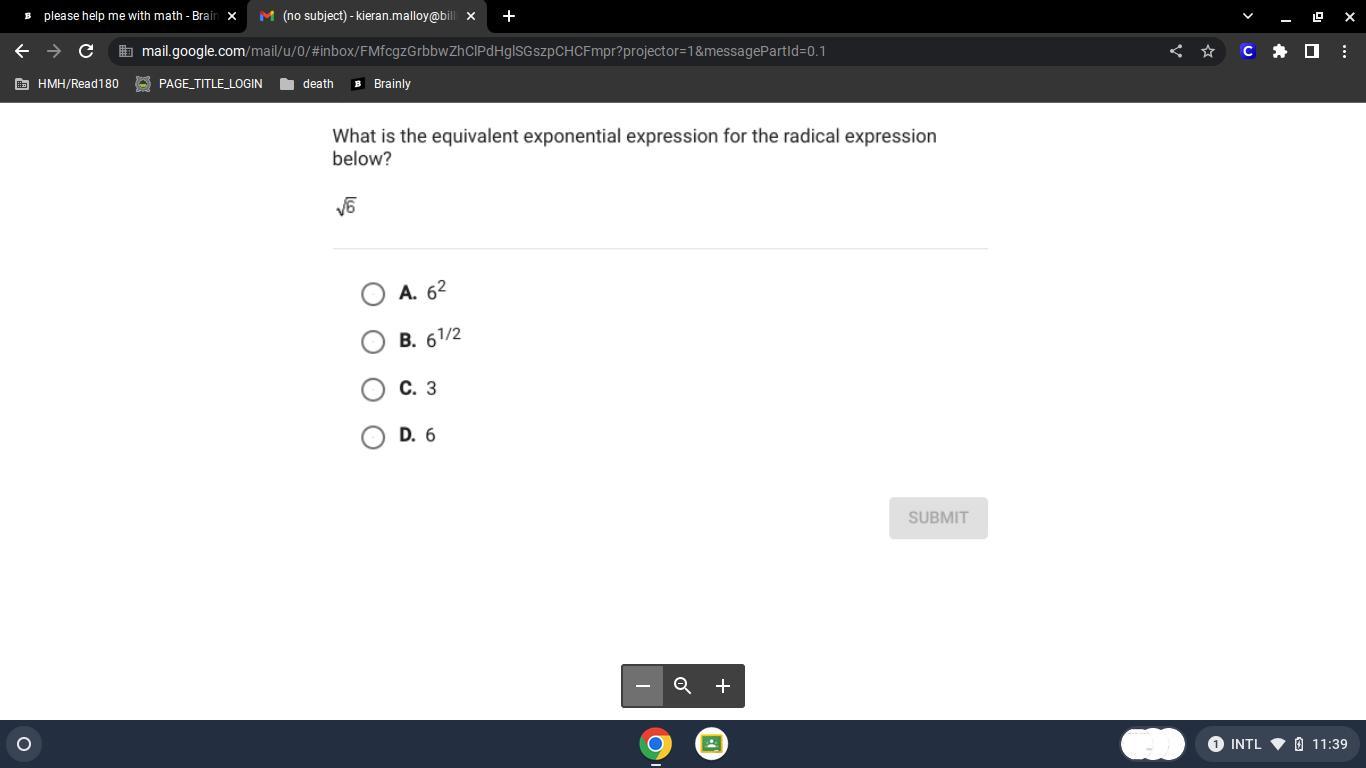
Answers
Answer:
B.) \(6^{\frac{1}{2}}\)
Step-by-step explanation:
Use the exponent rule that states \(a^{\frac{1}{m}}=\sqrt[m]{a}\). For this problem, let
a=6
m=2
So,
\(\sqrt6=6^{\frac{1}{2}}\)
find the point on the plane 4x − y + 4z = 40 nearest the origin.(x,y,z)=
Answers
The point on the plane 4x - y + 4z = 40 nearest the origin is (-3.048, -0.762, 6.467)
Given data ,
To find the point on the plane 4x - y + 4z = 40 nearest the origin, we need to minimize the distance between the origin and the point on the plane.
The normal vector to the plane 4x - y + 4z = 40 is given by (4,-1,4). To find the perpendicular distance from the origin to the plane, we need to project the vector from the origin to any point on the plane onto the normal vector. Let's choose the point (0,0,10) on the plane:
Vector from origin to (0,0,10) on the plane = <0-0, 0-0, 10-0> = <0,0,10>
Perpendicular distance from the origin to the plane = Projection of <0,0,10> onto (4,-1,4)
= (dot product of <0,0,10> and (4,-1,4)) / (magnitude of (4,-1,4))
= (0 + 0 + 40) / √(4^2 + (-1)^2 + 4^2)
= 40 / √(33)
To find the point on the plane nearest the origin, we need to scale the normal vector by this distance and subtract the result from any point on the plane. Let's use the point (0,0,10) again:
Point on the plane nearest the origin = (0,0,10) - [(40 / √(33)) / √(4^2 + (-1)^2 + 4^2)] * (4,-1,4)
= (0,0,10) - (40 / √(33)) * (4/9,-1/9,4/9)
= (0,0,10) - (160/9√(33), -40/9√(33), 160/9√(33))
= (-160/9√(33), -40/9√(33), 340/9√(33))
Hence , the point on the plane 4x - y + 4z = 40 nearest the origin is approximately (-3.048, -0.762, 6.467)
To learn more about distance between a point and plane click :
https://brainly.com/question/14442366
#SPJ1
Solving for Unknown Angle Measures
GEE
9
If angle 1 is 110°, what would the other angle
measures have to be in order for m | n and
all p?
4
Angle 2 =
3
n
Angle 3 =
2
Angle 4 =
m
Answers
Answer:
angle 4 is a full angle because it is represented full 110
Answer:
1 - 110
2 - 110
3 - 70
4 - 70