(Theoretical) The following is the limit of a Riemann sum. n
lim Σ √4+ 5k/n . 5/n
n --> [infinity] k=1
Compute this limit, by (a) identifying the correct definite integral it represents, and (b) performing the integration.
Answers
(a) The given limit represents the integral
\($$\int_{0}^{5} \sqrt{4 + 5x} \, dx$$\)
Given that the following is the limit of a Riemann sum:
\($\lim_{n\to\infty} \sum_{k=1}^{n} \sqrt{4 + \frac{5k}{n}} \cdot \frac{5}{n}$\)
To compute this limit, we need to identify the correct definite integral it represents and then perform the integration.
(a) Identifying the correct definite integral it represents
We can recognize that the above limit is a Riemann sum because the function
\($\sqrt{4 + \frac{5x}{n}}$\)
is continuous on the interval \($[0, 5]$\)
The interval\($[0, 5]$\) can be split into \($n$\) subintervals, each of length \($\frac{5}{n}$\).
The point \($x_k$\) in the \($k$\) subinterval is \($\frac{5k}{n}$\).
Therefore, the Riemann sum is
\($$\sum_{k=1}^{n} \sqrt{4 + \frac{5k}{n}} \cdot \frac{5}{n} = \frac{5}{n} \sum_{k=1}^{n} \sqrt{4 + \frac{5k}{n}}.$$\)
Thus, the limit of the Riemann sum can be written as
\($$\lim_{n\to\infty} \sum_{k=1}^{n} \sqrt{4 + \frac{5k}{n}} \cdot \frac{5}{n} = \lim_{n\to\infty} \frac{5}{n} \sum_{k=1}^{n} \sqrt{4 + \frac{5k}{n}}.$$\)
We can also see that the limit is equal to a definite integral
\($$\int_{0}^{5} \sqrt{4 + 5x} \, dx.$$\)
Thus, the given limit represents the integral
\($$\int_{0}^{5} \sqrt{4 + 5x} \, dx$$\)
(b) Performing the integration
We can perform the integration by making the substitution
\($u = 4 + 5x$.\)
Then \($du/dx = 5$\)
and \($dx = du/5$.\)
The limits of integration become
\($u(0) = 4$\)
and \($u(5) = 29$.\)
The integral becomes
\($$\int_{0}^{5} \sqrt{4 + 5x} \, dx = \frac{1}{5} \int_{4}^{29} \sqrt{u} \, du = \frac{1}{15}(29\sqrt{29} - 16).$$\)
Therefore, the limit of the Riemann sum is
\($$\lim_{n\to\infty} \sum_{k=1}^{n} \sqrt{4 + \frac{5k}{n}} \cdot \frac{5}{n} = \int_{0}^{5} \sqrt{4 + 5x} \, dx = \frac{1}{15}(29\sqrt{29} - 16).$$\)
Hence, the limit of the given Riemann sum is equal to the definite integral
\($\int_{0}^{5} \sqrt{4 + 5x} \, dx$.\)
We can perform the integration by making the substitution \($u = 4 + 5x$\)
and then applying the formula for the integral of
\($\sqrt{u}$.\)
After simplification, we obtain the value of the definite integral as
\($\frac{1}{15}(29\sqrt{29} - 16)$.\)
To know more about Riemann sum visit:
https://brainly.com/question/30404402
#SPJ11
Related Questions
Hey if you could help me with this it'd mean a lot I can't figure it out
L+S=17
3L+2S=46
What is S and what is L?
Answers
Answer:
L = 12 S = 5
Step-by-step explanation:
L+S=17
3L+2S=46
Multiply the first equation by -2
-2L -2S = -34
Then add it to the second equation
-2L -2S = -34
3L+2S=46
------------------
L = 12
Now we can find S
L+S = 17
12 + S = 17
Subtract 12 from each side
S = 17-12
S = 5
i need help with #5!! the sum is 4.5 but i don’t know a, y,
B, or d. PLZ ANSWERRR.
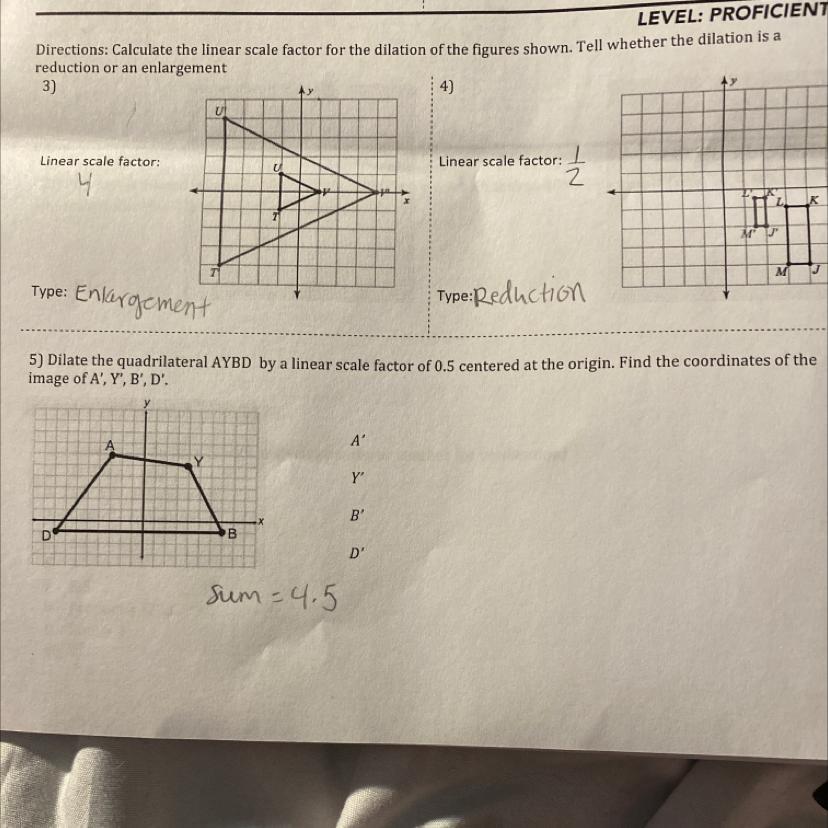
Answers
Answer:
A is -4, 6
Y is 4, 5
B is 7, -1
D is -8, -1
Find the value of k and yz if y is between x and z. x y = 3 k − 2 , y z = 7 k 4 , x z = 4 k 38
Answers
Considering that y is between x and z, we have that:
The value of k is of k = 6.The length of yz is 46 units.How to find the value of k and of yz?We consider that y is between x and z, hence the length of the segment is given by:
xz = xy + yz
The separate lengths are given as follows:
xz = 4k + 38.xy = 3k - 2.yz = 7k + 4.Hence:
4k + 38 = 3k - 2 + 7k + 4.
4k + 38 = 10k + 2
6k = 36
k = 6.
Hence the length of yz is given by:
yz = 7k + 4 = 7(6) + 4 = 42 + 4 = 46 units.
A similar problem, in which the length of a line segment is found, is given by https://brainly.com/question/24778489
#SPJ1
Nick just received his test back. He scored a 24 out of a possible 60 points. His teacher told him the mean score on the test was a 35, with a standard deviation of 6. What is nick's z-score?
Answers
Nick's z -score is -1.833.
According to the given question.
Total points scored by Nick, x = 24
Mean score for the test was, μ = 35
Standard deviation, σ = 6
As, we know that z-score can be caluated by using the formula
z = (x - μ)/σ
Where, x is a score
μ is mean score
σ is standard deviation
z is z-score
Therefore, Nick's z-score is given by
z = (24 - 35)/6
z = -1.833
ence, Nick's z -score is -1.833.
Find out more information about z-score here:
https://brainly.com/question/15016913
#SPJ4
All Things Algebra), 2013
After falling 17°, the
temperature of the lake
is now 24. What was the
starting temperature?(Write an equation to represent the problem)
Answers
Answer:
43°
x-17=24
Step-by-step explanation:
the tempertaure fell 17° and now its 24° so to get there you would have to subtract
x-17°=24°
43°
The first two photos are the four choices, and the third photo is figure 1. Help please!!Part A Select the correct sketch of the electric field of a quadrupole, two positive and two negative charges arranged as in Figure 1). + Submit Resuest Answer Figure 1 of 1 o + + Submit Provide Feedback
Answers
The correct sketch of the electric field of a quadrupole is option D. This is because a quadrupole consists of two positive charges and two negative charges arranged in a specific pattern that creates a unique electric field.
A quadrupole is a type of electric charge configuration in which two positive and two negative charges are arranged in a specific pattern. The positive and negative charges are arranged in such a way that they create a unique electric field that is used in many scientific applications, such as particle accelerators and mass spectrometers.
The electric field of a quadrupole is characterized by its unique shape. It is made up of two components: a quadrupolar component and a dipolar component. The quadrupolar component is stronger than the dipolar component and gives the field its characteristic four-lobed shape.
Option D is the correct sketch of the electric field of a quadrupole because it shows the four-lobed shape that is characteristic of a quadrupole.
To learn more about “charge” refer to the https://brainly.com/question/18102056
#SPJ11
D
Question 4
True or False:4.65 is less than square root 32 is
True
False
Answers
Scott invested a total of $6300 at two separate banks. One bank pays simple interest of 10% per year while the other pays simple interest at a rate of 9% per year. If Scott eamed $598.00 in interest during asingle year, how much did he have on deposit in gach bank?
Answers
Answer:
\(\begin{gathered} A_1=x=\operatorname{\$}3,100 \\ \\ A_2=y=\operatorname{\$}3,200 \end{gathered}\)Explanation: Scott Invested in two banks, and each bank paid 9% and 10% yearly interest. the total amount invested was $6300 and the Interest earned in the first year is $598. We have to find the amount invested in each bank.
Mathematical Formula:
let us say that amount x was invested in the first bank and amount y was invested in the second bank, considering this we can write the following equation for the total money invested:
\(\begin{gathered} x+y=\$6300\Rightarrow(1) \\ \end{gathered}\)Similarly, the following is the equation for the total Interest earned in the first year.
\((0.1)x+(0.09)y=\$598\Rightarrow(2)\)Equation (1) and (2) are two linear simultaneous equations:
\(\begin{cases}x+y={6300} \\ (0.1)x+(0.09)y={598}\end{cases}\)The graphical solution to the above system is as follows:
Therefore the amount invested in each bank is:
\(\begin{gathered} x=\$3,100 \\ y=\$3,200 \\ \\ \because\rightarrow \\ x+y=\$3,100+3,200=\$6,300\rightarrow\text{ \lparen Checks out\rparen} \end{gathered}\)Scott invested $3,100 in the first bank and in the second bank, he invested $3,200.

A snowboarder slides up from the bottom of a half-pipe and comes down again, sliding with little resistance on the snow. Her height above the top edge of the pipe t seconds after starting up the side is -4.9 t2 + 11 t - 4. (a) What is her height at t = 0? Choose one Her height at t= 0 is 4 meters the edge of the half-pipe. (b) After how many seconds does she reach the top edge? Return to the edge of the pipe? NOTE: Give numerical answers accurate to 3 decimal places. She reaches the top of the edge after seconds. She returns to the edge of the pipe when t = seconds. (c) How long is she in the air? NOTE: Give your answer accurate to 3 decimal place
Answers
A snowboarder starts at a height of -4 meters above the edge of a half-pipe, reaches the top edge after approximately 2.493 seconds, returns to the edge of the pipe at t = -0.253 seconds, and spends approximately 2.746 seconds in the air.
(a) To find the height at t = 0, we substitute t = 0 into the equation:
Height at t = 0 = -4.9(0)^2 + 11(0) - 4 = -4.
Therefore, her height at t = 0 is -4 meters above the edge of the half-pipe.
(b) To find when she reaches the top edge, we need to find the value of t where her height is equal to zero. We set the equation equal to zero and solve for t:
-4.9t^2 + 11t - 4 = 0.
Using the quadratic formula, t = (-b ± √(b^2 - 4ac)) / (2a), where a = -4.9, b = 11, and c = -4.
Calculating the values:
t = (-11 ± √(11^2 - 4(-4.9)(-4))) / (2(-4.9)).
Simplifying further:
t = (-11 ± √(121 - 78.4)) / (-9.8).
t = (-11 ± √42.6) / (-9.8).
Evaluating the two possibilities:
t ≈ -0.253 seconds or t ≈ 2.493 seconds.
She reaches the top edge after approximately 2.493 seconds.
To find when she returns to the edge of the pipe, we look for the other value of t that makes the height zero. Therefore, she returns to the edge of the pipe at t = -0.253 seconds.
(c) To determine how long she is in the air, we calculate the time from the moment she leaves the edge of the pipe until she returns. This is the time between t = -0.253 seconds and t = 2.493 seconds.
Time in the air = 2.493 - (-0.253) ≈ 2.746 seconds.
Therefore, she is in the air for approximately 2.746 seconds.
To know more about snowboarder,
https://brainly.com/question/30810376
#SPJ11
If f(x)=x-3/x, g(x)= x+3, and h(x)=2x+1, what is
Answers
Answer:
Step-by-step explanation:
https://brainly.com/question/20086687?answeringSource=greatJob%2FquestionPage%2F3
Graph the inequality.
y2-3x+4
Answers
The government buys new weapons systems. The manufacturers of weapons pay their employees. The employees spend this money on goods and services. The firms they buy goods and services from pay their employees and the local economy expands. This illustrates
Answers
The government's purchase of new weapons systems has a ripple effect that stimulates economic growth. When the government buys weapons systems from manufacturers, it injects money into the industry, enabling manufacturers to pay their employees.
These employees then spend their earnings on various goods and services, which benefits other businesses. As a result, those businesses can hire more employees and contribute to the expansion of the local economy.
This process can be understood through the concept of the multiplier effect. The initial government spending on weapons systems creates a chain reaction of increased economic activity. The manufacturers, upon receiving payment, allocate those funds to employee salaries, thereby boosting the income and purchasing power of their workers.
These employees, in turn, utilize their income to make purchases from different firms, such as grocery stores, restaurants, or service providers. Consequently, these businesses experience a rise in demand, allowing them to hire more employees to meet the increased consumer needs. This cycle continues, leading to a broader expansion of the local economy as money circulates and creates additional income and employment opportunities.
Learn more about Employees:
brainly.com/question/17134550
#SPJ11
Solve this too please:
1) 91+35--->___+___=___
2) 16+15--->___+___=___
3) 84+77--->___+___=___
4) 25+49--->___+___=___
5) 46+31--->___+___=___
6) 44+56--->___+___=___
7) 82+35--->___+___=___
8) 57+9--->___+___=___
Answers
Answer:
1) 91+35=90+40+130
2) 16+15=20+20=40
3) 84+77=80+80=160
4) 25+49=30+50+80
5) 46+31=50+30=80
6) 44+56=40+60=100
7) 82+35=80+40=120
8) 57+9=60+10=70
Based on the pattern, what are the next two terms of the sequence? 9, 15, 21, 27, . . .




Answers
Answer: 33,39
Step-by-step explanation:
Counting by 6's
Please help me with this homework show me how you get it and the answer

Answers
Answer:
Step-by-step explanation:
V = 1/3πr^2h
Putting values
V = 1/3(3.14)(4)^2(3)
= 50.24
The GCF of two whole numbers is the ________. A smallest whole number that divides evenly into both numbers B largest whole number that divides evenly into both numbers C smallest whole number that both numbers divide into evenly D largest whole number that both numbers divide into evenly
Answers
Answer:
Largest whole number that divides evenly into both numbers.
Step-by-step explanation:
GCF is greatest common factor. It is also known as LCM of lowest common multiple.
It is the set of whole numbers that divides evenly into all numbers with zero remainder.
For example, three numbers are 8,12 and 20.
The factors of 8 are: 1, 2, 4, 8
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 20 are: 1, 2, 4, 5, 10, 20
The GCF of these three numbers is 4. 4 divides evenly into all numbers.
Hence, the correct option is (B).
Answer:
A and E
Step-by-step explanation:
hope yall have a great day!
Help needed ASAP will give brainliest

Answers
Answer:
I guess the answer is going to be 9/5
C=2 4 6 3 6 9 4 8 12 find the determinant and inverse of c
Answers
Answer:
The determinant of C is zero and does not have inverse.
Step-by-step explanation:
Let \(C = \left[\begin{array}{ccc}2&4&6\\3&6&9\\4&8&12\end{array}\right]\), since it is a matrix with 3 rows and 3 columns, we can determine its determinant by the Sarrus' rule:
\(\det(C) = \left|\begin{array}{ccc}2&4&6\\3&6&9\\4&8&12\end{array}\right|\)
\(\det(C) = (2)\cdot (6)\cdot (12)+(3)\cdot (8)\cdot (6)+(4)\cdot (4)\cdot (9)-(4)\cdot (6)\cdot (6)-(3)\cdot (4)\cdot (12)-(2)\cdot (8)\cdot (9)\)
\(\det (C) = 0\)
Since the determinant of C is equal to zero, then we conclude that C does not have an inverse according to the following definition of inverse matrix. That is:
\(C^{-1} = \frac{1}{\det(C)}\cdot adj(C)\) (1)
Where \(adj(C)\) is the adjugate matrix of C, defined as the transpose of the cofactor matrix of C.
The result of this expression is undefined due to the determinant.
Choose ASA, SAA, or neither
to describe this figure.
A
B
ASA
SAA
neither

Answers
Answer:
SAA
Step-by-step explanation:
there is a side, and vertical angles equal eachother so it would be SAA
Help meh please because I don’t understand this

Answers
Answer:
\(\textsf{a) \quad $\dfrac{2}{5}$}\)
\(\textsf{b) \quad $\dfrac{5}{2}$}\)
Step-by-step explanation:
Question a)Given expression:
\(\left(\dfrac{4}{25}\right)^{\frac{1}{2}}\)
Rewrite 4 as 2² and 25 as 5²:
\(\implies \left(\dfrac{2^2}{5^2}\right)^{\frac{1}{2}}\)
\(\textsf{Apply the exponent rule} \quad \left(\dfrac{a}{b}\right)^c=\dfrac{a^c}{b^c}:\)
\(\implies \dfrac{(2^2)^{\frac{1}{2}}}{(5^2)^{\frac{1}{2}}}\)
\(\textsf{Apply the exponent rule} \quad (a^b)^c=a^{bc}:\)
\(\implies \dfrac{2^{(2\cdot\frac{1}{2})}}{5^{(2\cdot\frac{1}{2})}}\)
\(\implies \dfrac{2^1}{5^1}\)
\(\implies \dfrac{2}{5}\)
Question b)Given expression:
\(\left(\dfrac{4}{25}\right)^{-\frac{1}{2}}\)
Rewrite 4 as 2² and 25 as 5²:
\(\implies \left(\dfrac{2^2}{5^2}\right)^{-\frac{1}{2}}\)
\(\textsf{Apply the exponent rule} \quad \left(\dfrac{a}{b}\right)^c=\dfrac{a^c}{b^c}:\)
\(\implies \dfrac{(2^2)^{-\frac{1}{2}}}{(5^2)^{-\frac{1}{2}}}\)
\(\textsf{Apply the exponent rule} \quad (a^b)^c=a^{bc}:\)
\(\implies \dfrac{2^{(2\cdot -\frac{1}{2})}}{5^{(2\cdot -\frac{1}{2})}}\)
\(\implies \dfrac{2^{-1}}{5^{-1}}\)
\(\textsf{Apply the exponent rule} \quad a^{-n}=\dfrac{1}{a^n}:\)
\(\implies \dfrac{1}{2^1 \cdot 5^{-1}}\)
\(\implies \dfrac{1}{2 \cdot 5^{-1}}\)
\(\textsf{Apply the exponent rule} \quad \dfrac{1}{a^{-n}}=a^n:\)
\(\implies \dfrac{5^1}{2}\)
\(\implies \dfrac{5}{2}\)
yo i need help please no links i just need the answer to pass my exit ticket please i’ll give u a brainliest

Answers
Answer:
approximately 15 ice cones
Step-by-step explanation:
volume of cylinder is V=πr2h
volume of cone is V=πr2h
3
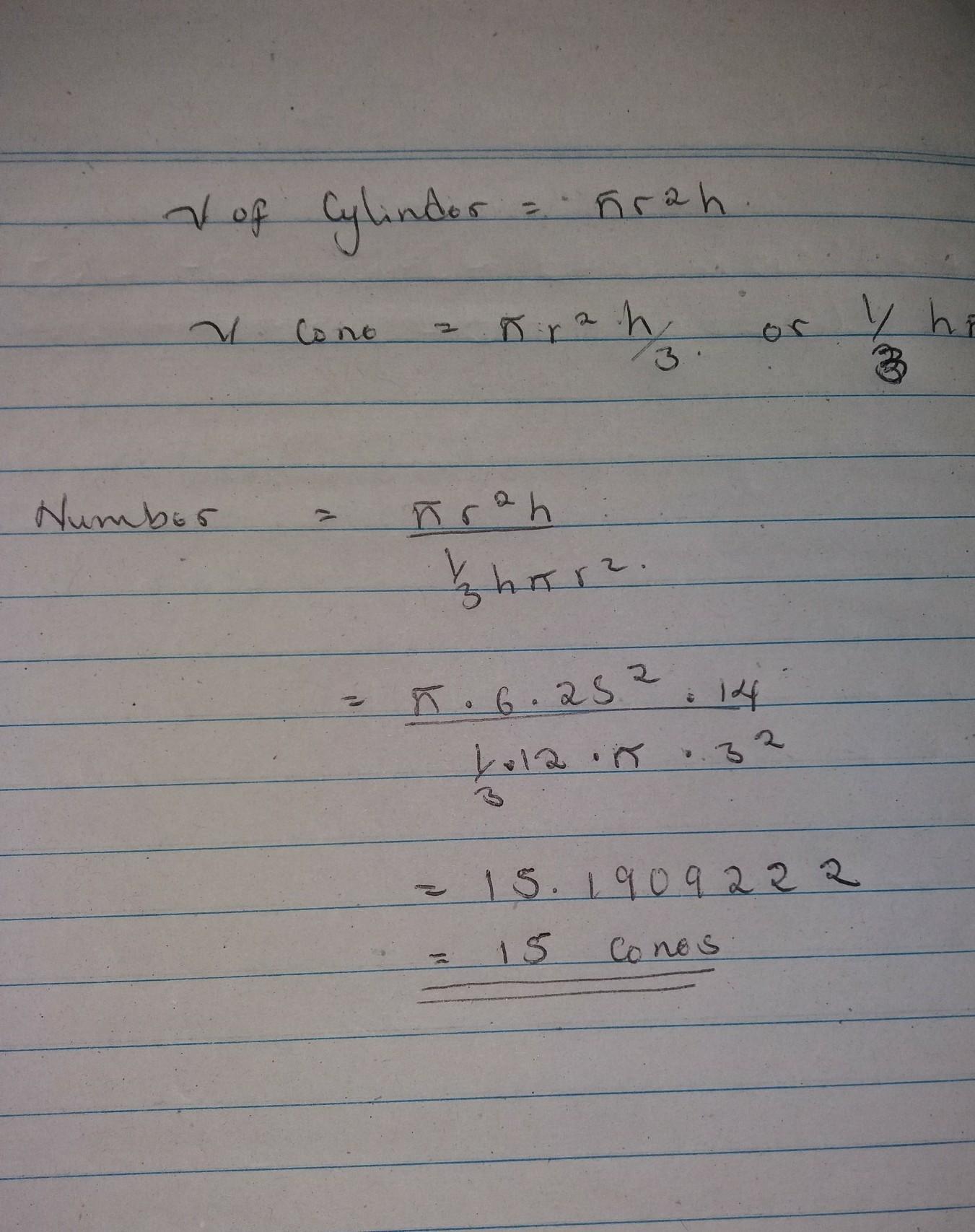
If you anwser the question i give you brainly



Answers
The proportional relationship graph that shows the situation is: Graph C.
What is a Proportional Relationship?A proportional relationship is defined as y = kx, where k is the constant of proportionality between x and y, and k = y/x.
Given the equation, M = 3n,
k = 3.
Thus, the graph that has a constant of proportionality (k) of 3, will correspond to the situation.
In graph C, using a point, (400, 1,200), we have:
k = 1,200/400
k = 3
Therefore, the graph that corresponds to the situation is: C.
Learn more about proportional relationship on:
https://brainly.com/question/23318486
#SPJ1

When you’re multiplying or dividing same sign numbers, what will your product or quotient be?
Answers
When you multiply two integers with the same signs, the result is always positive. Just multiply the absolute values and make the answer positive. When you multiply two integers with different signs, the result is always negative.
Please help me solve this quickly! Will give brainliest!

Answers
Answer:
y = 5\(\sqrt{6}\)
Step-by-step explanation:
JLT forms the special 90-60-30 right triangle and the side length for the given measure follows as 2a-a\(\sqrt{3}\)-a
since the side length that sees 90 degrees is 10 then x = 5
according to Euclidian theorem :
y^2 = LK*KI (LK = 15 -x, KI = 15)
y^2 = 10*15
y^2 = 150 find the root for both sides
y = 5\(\sqrt{6}\)
Sara has 16 red flowers and 24 yellow flowers. She wants to make bouquets with the same number of each color flower in each bouquet.
Part A: What is the greatest number of bouquets she can make?
(Include the numerical answer only.)
Answers
Answer:
8
Step-by-step explanation:
make 8 bouquets: Each bouquet will have 2 red flowers and 3 yellow flowers.
Let g(x)=3 x+2 and f(x)= x-2 / 3 . Find each value.
g(f(-4))
Answers
The value for g(f(-4)) = -4
What are the domain of the function g(f(-4))?
Given:
g(x) = 3 x+2 and f(x)= x-2 / 3
Take, f(x) = x-2 / 3
substitute x = -4 into the function f(x). Then:
f(-4) = (-4)-2/ 3
f( -4) = -6/3
f( -4) = -2
Now, the next step is to substitute f(-4) into the function g(x)
g(x) = 3 x+2
g(f( x)) = 3 x+2
g(f(-4)) = 3(-2) +2
g(f(-4) = -6+2
g(f(-4) = -4
To learn more about domain, visit
brainly.com/question/14517703
#SPJ4
Please help me by explain step by step.
Identify the points of intersection for y=x^2-3x-8 and y=2
Answers
Answer:
x=5, and x=-2
Step-by-step explanation:
A point of intersection between the two would be when they equal each other:
x^2-3x-8=2
x^2-3x-10=0
(x-5)(x+2)=0
x=5, and x=-2
I hope this helps! :)
Find the area of the trapezoid
A. 168 in^2
B. 94.5 ft^2
C. 72 ft^2
D. 84 ft^2

Answers
Answer:
D. 84 ft^2
Step-by-step explanation:
Formula for area of a trapezoid:
\(A=\frac{a+b}{2} h\)
where a and b = bases and h = height
The trapezoid shown has the following dimensions
base 1 = 9ft
base 2 = 12ft
height = 8ft
Using the following information we plug in the values into the formula
\(A=\frac{9+12}{2} \\9+12=21\\\frac{21}{2} =10.5\\10.5*8=84\)
Hence, the area of the trapezoid is 84ft² and your answer is D
How many 4 1/2 feet pieces of rope can be cut from the 48 foot pieces of rope
Answers
Answer:
Below
Step-by-step explanation:
48 ft / 4.5 ft/piece = 10 2/3 = ~ 10 pieces with 2/3 ft left over
what is 4x-3 i need a 6th grade explanation
Answers
Answer:
-12?
Step-by-step explanation: