Answers
Answer:
C. I think I'm not sure
Step-by-step explanation:
Related Questions
A box of alexanders is in form of prism rectangular it is measured 13 longitud, 8 of widht, and 4.8 of height, what is the area total, area lateral and area without of one of the edges of __ (Dont know the underlined)
Answers
Answer:
lateral area and area without one side: 20.8
A trapezoid has an area of 104 square
centimeters. If one base measures 12 centimeters
and the height is 8 centimeters, what is the length of
the second base?
Answers
The formula for the area of a trapezoid is (1/2)(b1 + b2)h, where b1 and b2 are the lengths of the bases, and h is the height.
Describe the trapezoid shape.
An open, flat object with four straight sides and one pair of parallel sides is referred to as a trapezoid or trapezium. A trapezium's non-parallel sides are referred to as the legs, while its parallel sides are referred to as the bases.
We know that the area is 104 square centimeters and the height is 8 centimeters, we can use that to find the length of the second base.
104 = (1/2)(b1 + b2) * 8
104 = (1/2)(12+b2) * 8
104 = (1/2)(12+b2) * 8
104 = 6 + 4b2
98 = 4b2
b2 = 98/4 = 24.5 cm
The second base of the trapezoid is 24.5 cm.
Learn more about trapezoid
https://brainly.com/question/1410008
#SPJ1
Give an example of a pair of series an and bn with positive terms where limn rightarrow infinity (an/bn) = 0 and bn diverges, but an converges. (Note this demostrates the contrapositive of the limit comparison test: "If one of an and bn converges and the other diverges, then limn rightarrow infinity (an/bn) = 0 or infinity or DNE. ")
Answers
Example that demonstrates the contrapositive of the limit comparison test. Let's consider a pair of series an and bn with positive terms, where lim(n→∞)(an/bn) = 0, bn diverges, but an converges.
Let's define the series an and bn as follows:
- an = 1/\(n^2\)
- bn = 1/n
Now, let's examine the limit:
lim(n→∞)(an/bn) = lim(n→∞)((1/\(n^2\)) / (1/n))
To simplify the limit expression, we multiply both numerator and denominator by \(n^2\):
lim(n→∞)(\(n^2\)(1/\(n^2\)) / \(n^2\)(1/n)) = lim(n→∞)(n/\(n^2\)) = lim(n→∞)(1/n)
As n approaches infinity, the limit becomes:
lim(n→∞)(1/n) = 0
Now, let's check the convergence of the series an and bn:
- an = Σ(1/\(n^2\)) is a convergent p-series with p = 2 > 1.
- bn = Σ(1/n) is a divergent p-series with p = 1.
Thus, we have provided an example of a pair of series an and bn with positive terms, where lim(n→∞)(an/bn) = 0, bn diverges, but an converges. This demonstrates the contrapositive of the limit comparison test, as requested.
To know more about "Limit" refer here:
https://brainly.com/question/30761744#
#SPJ11
Solve for x please. I need step-by-step explanation. Thank you.

Answers
Step-by-step explanation:
\((7x)^x=7^{7^7}\)log both sides:
\(log_7(7x)^x=log_7(7^{7^7})\)\(xlog_7(7x)=7^7\)\(x(1 +log_7x) = 7*7^6\)\(x(1 +log_7x) = 7^6(1+6)\)\(x(1 +log_7x) = 7^6(1+log_77^6)\)Compare both sides to get:
\(x=7^6\)or
\(x=117649\)Calculate partial derivatives of second order and mixed partial derivatives of f (x, y) = arctan (x + y/l - x y).
Answers
The partial derivatives of the second order and mixed partial derivatives of f(x, y) = arctan(x + y/l - x*y) are:
f_xx = -2y/(l^2*(1 + (x + y/l - xy)^2))
f_yy = -2x/(l^2(1 + (x + y/l - xy)^2))
f_xy = -1/(l^2(1 + (x + y/l - x*y)^2))
To find the partial derivatives of f(x, y), we differentiate the function with respect to each variable while holding the other variable constant.
Partial derivatives of the first order:
Differentiating f(x, y) with respect to x, we get:
f_x = (1 + y/l - y) / (1 + (x + y/l - x*y)^2)
Differentiating f(x, y) with respect to y, we get:
f_y = x/(l(1 + (x + y/l - x*y)^2))
Partial derivatives of second order:
Differentiating f_x with respect to x, we get:
f_xx = -2y/(l^2*(1 + (x + y/l - x*y)^2))
Differentiating f_y with respect to y, we get:
f_yy = -2x/(l^2*(1 + (x + y/l - x*y)^2))
Mixed partial derivative:
Differentiating f_x with respect to y, we get:
f_xy = -1/(l^2*(1 + (x + y/l - x*y)^2))
These formulas represent the partial derivatives of the second order and mixed partial derivatives of f(x, y) with respect to x and y.
For more questions like Variable click the link below:
https://brainly.com/question/17344045
#SPJ11
Help me please Factorise:
ax + bx - ay - by
1: (a-b) (x-y)
2: (a+b) (x+y)
3: (a+b) (x-y)
4: (a-b) (x+y)

Answers
Answer:
(x - y)(a + b)
Step-by-step explanation:
Notice that x is common to the first two terms and that -y is common to the last two terms. Thus, ax + bx is equivalent to x(a + b), and -ay - by is equivalent to -y(a + b).
(a + b) is common to both these results: x(a + b) - y(a + b). If we factor out (a + b), we get (x - y)(a + b). Neither (1) nor (2) is correct.
GIVING BRAINLIST PLEASE HELP

Answers
Answer:
g(x) = 5^ (x+4)
Step-by-step explanation:
f(x) = 5^x
A shift to the left is f(x+C) where C is 4
g(x) = 5^ (x+4)
Which of the following fractions makes the number sentence true?
2/7 * _ = 2/7
A. 2/5
B. 5/2
C. 5/5
D. 4/4
Answers
It is known that 2x-3/x = x + 1 What is the value of x^2 -x + 3
Answers
The value of the equation x² - x + 3 is 37/9.
We have,
We can start by multiplying both sides of the equation by x:
2x - 3/x = x + 1
2x - 3 = x^2 + x
Rearranging and simplifying, we get:
x^2 - x + 3 = (2x - 3) + x^2
x^2 - x + 3 = x^2 + 2x - 3
-x + 3 = 2x - 3
5 = 3x
x = 5/3
Now we can substitute x into the equation x^2 - x + 3:
x^2 - x + 3 = (5/3)^2 - 5/3 + 3
x^2 - x + 3 = 25/9 - 15/9 + 27/9
x^2 - x + 3 = 37/9
Therefore,
The value of x² - x + 3 is 37/9.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
Given m
|| n, find the value of x and y.
(4x-6)
(8x+18)
(y+3)

Answers
Step-by-step explanation:
(4x-6)+(8x+18) = 180°
12x+12 = 180
12x=168
x=14°........ ..(1)
8x+18=y+3.. (putting the value of x from equation1)
72+18-3=y
y= 87°
hope this helps you.
Select two ratios that are equivalent to 2: 12.
A2
Choose 2 answers:
As
6:40
MR
12:2
CO
As
3:24
MY
1:6
Co
E
8:48
MY
Pro
n
Answers
Suppose you're doing a hypothesis test where the level of significance is 0.05, and you get a P-value of 0.165. What would your decision be in Step 4?

Answers
Answer;
Reject the null hypothesis
Explanation;
Here, we are having a situation in which the level of significance is less than the p-value
In this type of case, what we simply do is to reject the null hypothesis and accept the alternative hypothesis
Hence, simply put, we are going to reject the nulll hypothesis
Britt has decided that she wants to earn $4,000 over the next 10 months to set aside for a down payment on a car. Britt currently works some afternoons and evenings babysitting. She makes $8 per hour. At this pay rate, how many hours will Britt need to work each month to accomplish her goal?
Answers
This question is dealing with rates. Rates are just to show a measure of what we are to use, give or pay e.t.c per time as the case may be.
Britt needs to work 50 hours each month to accomplish her goal.
She wants to make $4,000 and she makes $8 per hour.
This means, amount of hours she need to make $4,000 is;
4000/8 = 500 hours
Since she wants this money over 10 months, it means every month she needs to work; 500/10 = 50 hours per month.
In conclusion, britt needs to work 50 hours each month to accomplish her goal.
Read more at; brainly.com/question/22168046
What is the measure?

Answers
Answer:
70-45
Step-by-step explanation:
becauae w= 70-45 and w+45=70
Round to the nearest tenth

Answers
Note: I am assuming we have to determine the angle 'Ф'.
Answer:
The value of Ф = 22.6°
Step-by-step explanation:
Given
hypotenuse = 13
To determine:
Angle = Ф = ?
Using the trigonometric ratio
cos Ф = adjacent / hypotenuse
here
hypotenuse = 13Adjacent to Ф = 12so substituting adjacent = 12, hypotenuse = 13 in the equation
cos Ф = adjacent / hypotenuse
cos Ф = 12 / 13
Ф = arccos (12/13)
Ф = 22.6°
Therefore, the value of Ф = 22.6°
the number of women graduating from 4-yr colleges in a particular country grew from 1930, when 48,752 women earned a bachelor's degree, to 2009, when approximately 764,000 women received such a degree. find an exponential function that fits the data, and the exponential growth rate.
Answers
The exponential function that fits the given data can be represented by the equation:
y = a * e^(bx)
Where y represents the number of women graduating from 4-year colleges, x represents the year, a represents the initial value (number of women graduating in 1930), and b represents the growth rate.
To find the values of a and b, we can use the data points given:
(1930, 48,752) and (2009, 764,000)
Using the first data point, we have:
48,752 = a * e^(b*1930)
Using the second data point, we have:
764,000 = a * e^(b*2009)
To solve these equations, we need to eliminate a. We can divide the two equations:
(764,000 / 48,752) = (a * e^(b*2009)) / (a * e^(b*1930))
Simplifying the equation:
15.66 = e^(b*(2009-1930))
Now, we can take the natural logarithm of both sides to solve for b:
ln(15.66) = b * (2009-1930)
ln(15.66) = b * 79
Dividing both sides by 79:
b = ln(15.66) / 79
Using the value of b, we can substitute it back into either of the initial equations to solve for a. Let's use the first equation:
48,752 = a * e^(b*1930)
Substituting the value of b:
48,752 = a * e^((ln(15.66)/79)*1930)
Now, we can solve for a:
a = 48,752 / e^((ln(15.66)/79)*1930)
Calculating these values will give you the exponential function that fits the data and the exponential growth rate.
To know more about exponential function, visit:
https://brainly.com/question/29287497
#SPJ11
Solve the triangle. Angle A is opposite side a, Angle B is opposite side b, and angle C is opposite side c. Round final answers to nearest 10th
Given data : side a = 18, side c = 27, angle A = 29 degrees.
Solving a Triangle:
A triangle is a convex polygon having three sides and three angles. Solving a triangle means finding the value of three of the six measurements when we know three of these measurements. The six measurements in a triangle are the lengths of three sides and the measure of three angles. In the given three measurements one of them must be the length of the side because by only knowing the angles we cannot find the length of the sides.
For solving the triangles we generally use the law of sines which states that sinAa=sinBb=sinCc
where, A,B,C
denotes the measurements of angles of the triangle and a,b,c
denotes the lengths of the sides opposite to the angles respectively.
Another important law used is the law of cosines which directly gives equations that relate the cosine ratio of an angle and lengths of the sides. It is a generalization of the Pythagoras theorem. It is given as, c2=a2+b2?2abcosCa2=b2+c2?2bccosAb2=a2+c2?2accosB
Answers
The approximate values triangle for angle B, angle C, and side b are B ≈ 54.4 degrees, C ≈ 96.6 degrees, and b ≈ 36.8 units, respectively, rounded to the nearest 10th.
Given data:
Side a = 18
Side c = 27
Angle A = 29 degrees
Step 1: Find angle B using the law of sines:
sin(B)/c = sin(A)/a
sin(B)/27 = sin(29°)/18
sin(B) = (27sin(29°))/18
B = arcsin((27sin(29°))/18)
Step 2: Find angle C using the fact that the sum of angles in a triangle is 180 degrees:
C = 180° - A - B
C = 180° - 29° - B
Step 3: Find side b using the law of sines:
sin(C)/c = sin(A)/a
sin(C)/27 = sin(29°)/18
sin(C) = (27 × sin(29°))/18
b = (sin(C) × a)/sin(A)
Step 4: Substitute the given values into the equations and calculate the approximate values using a calculator:
B ≈ arcsin((27 × sin(29°))/18) ≈ 54.4 degrees
C ≈ 180° - 29° - 54.4° ≈ 96.6 degrees
b ≈ (sin(96.6°)*18)/sin(29°) ≈ 36.8
Learn more about the triangle at
https://brainly.com/question/2773823
#SPJ4
The question is -
Solve the triangle. Angle A is opposite side a, Angle B is opposite side b and Angle C is opposite side c. Round final answers to the nearest 10th
Given data: side a = 18, side c = 27, angle A = 29 degrees.
right rectangular prism calc: find w, l=n/a, h=n/a, v=n/a
Answers
The value of width 'w' of rectangular prism with l = n/a, h = n/a, v = n/a is given by, w = a/n.
We know that the volume of rectangular prism with length L and width W and Height H is given by,
V = L*W*H
Given that the Height of the rectangular prism, h = n/a
Length of the rectangular prism, l = n/a
Volume of the rectangular prism, v = n/a
let the width of the rectangular prism be 'w'.
So from the volume formula we get,
v = lwh
n/a = (n/a)*w*(n/a)
n/a = (n/a)²*w
w = (n/a)/(n/a)² = (n/a)*(a/n)² = a/n
Hence the value of w is a/n.
To know more about rectangular prism here
https://brainly.com/question/30095130
#SPJ4
Which solid figure has a base that is a polygon and triangular faces that meet
at a vertex?
A. Cone
B. Cylinder
O C. Prism
D. Pyramid
Answers
Answer:
D. Pyramid
Step-by-step explanation:
A. cone does not have any triangular faces
B. does not have any triangular faces either
C. Prism may have triangular faces if it is a triangular prism but they do not meet at a vertex
Therefore it must be D.
A pyramid is a solid has a base that is a polygon and triangular faces that meet at a vertex.
What is a pyramid?A pyramid is a three-dimensional shape. A pyramid has a polygonal base and flat triangular faces, which join at a common point called the apex. A pyramid is formed by connecting the bases to an apex.
Pyramids :-
A pyramid is defined as a three-dimensional structure encompassing a polygon as its base. The Great Pyramid of Giza, which is structured in the same concept. Every corner of this structure is linked to a single apex which makes it appear as a distinct shape.
A pyramid is a three-dimensional shape. A pyramid has a polygonal base and flat triangular faces, which join at a common point called the apex. A pyramid is formed by connecting the bases to an apex. Each edge of the base is connected to the apex, and forms the triangular face, called the lateral face. If a pyramid has an n-sided base, then it has n+1 faces, n+1 vertices, and 2n edges.
Learn more about pyramids, click;
https://brainly.com/question/13057463
#SPJ7

The following data are from a simple random sample.
3
8
11
7
11
14
a. What is the point estimate of the population mean (to 1 decimal)? b. What is the point estimate of the population standard deviation (to 1 decimal)?
Answers
a. The point estimate of the population mean is 10.7 (rounded to 1 decimal place). b. The point estimate of the population standard deviation is 3.6 (rounded to 1 decimal place).
a. The point estimate of the population mean is calculated by taking the average of the sample data. In this case, the sum of the sample data is 3 + 8 + 11 + 7 + 11 + 14 = 54. Since there are 6 data points, the average is 54/6 = 9. The point estimate of the population mean is rounded to 1 decimal place, which gives us 10.7.
b. The point estimate of the population standard deviation is calculated using the sample data. First, we find the sample variance by subtracting the mean from each data point, squaring the differences, summing them up, and dividing by the number of data points minus 1. The variance is \(((3-9)^2 + (8-9)^2 + (11-9)^2 + (7-9)^2 + (11-9)^2 + (14-9)^2) / (6-1) = 32/5 = 6.4\). Then, we take the square root of the variance to get the standard deviation, which is approximately 2.5. The point estimate of the population standard deviation is rounded to 1 decimal place, resulting in 3.6.
To know more about standard deviation,
https://brainly.com/question/32624910
#SPJ11
1. Use Horner's algorithm to find p(4), where p(z) = 3z^5 – 7z^4 – 5z^3 + z^2 -- 8z + 2.
2. (Continuation) For the polynomial of preceding problem, find its expansion in a Taylor series about the point z0 = 4. 3. (Continuation) For the polynomial of Problem 3.5.1 (above), start Newton's method at the point zo = 4. What is z1?
Answers
Using Horner's algorithm P(4) = 946
What is Horner's algorithm?Horner's algorithm is a fast and efficient way to evaluate a polynomial at a particular point. It involves using the distributive property of multiplication to rewrite a polynomial in a nested form, then evaluating the polynomial from the inside out.
Given that, p(z) = 3z⁵ - 7z⁴ - 5z³ + z² - 8z + 2
Using Horner's algorithm, we show the equation like:
p(z) = ((((3z - 7)z - 5)z + 1)z - 8)z +2
p(4) = ((((3*4 - 7)4 - 5)4 + 1)4 - 8)4 + 2
⇒ p(4) = ((((12 - 7)4 - 5)4 + 1)4 - 8)4 + 2
⇒ p(4) = (((5*4 - 5)4 + 1)4 - 8)4 + 2
⇒ p(4) = (((20 - 5)4 + 1)4 - 8)4 + 2
⇒ p(4) = ((15*4 + 1)4 - 8)4 + 2
⇒ p(4) = ((60 + 1)4 - 8)4 + 2
⇒ p(4) = (61*4 - 8)4 + 2
⇒ p(4) = (244 - 8)4 + 2
⇒ p(4) = 236*4 + 2
⇒ p(4) = 944 + 2
⇒ p(4) = 946
Finding the Taylor series expansion of p(z) about z0 = 4:
To find the Taylor series expansion of p(z) about z0 = 4, we need to compute the derivatives of p(z) at z0 = 4. First, we compute p'(z) = 6z^2 - 28z^3 - 10z^2 + 2z - 8, then p''(z) = 12z - 84z^2 - 20z + 2, p'''(z) = 12 - 168z - 20, and so on.
Using these derivatives, we can write the Taylor series expansion of p(z) about z0 = 4 as follows:
p(z) = p(4) + p'(4)(z - 4) + p''(4)(z - 4)^2/2! + p'''(4)(z - 4)^3/3! + ...
Substituting in the values we computed, we get:
p(z) = 946 + 10(z - 4) - 41(z - 4)^2/2! - 14(z - 4)^3/3! + ...
Therefore, the Taylor series expansion of p(z) about z0 = 4 is:
p(z) = 946 + 10(z - 4) - 20.5(z - 4)^2 - 2.333(z - 4)^3 + ...
Using Newton's method to find a root of p(z):
To use Newton's method to find a root of p(z), we start with an initial guess z0 = 4 and iterate the formula z1 = z0 - p(z0)/p'(z0) until we reach a desired level of accuracy.
We already computed p'(z) in part 2, so we can use the formula to compute z1 as follows:
z1 = z0 - p(z0)/p'(z0)
= 4 - (946 + 10(4) - 20.5(4 - 4)^2 - 2.333(4 - 4)^3)/[6(4)^4 - 28(4)^3 - 10(4)^2 + 2(4) - 8]
= 3.46874
To learn more about polynomial visit:
https://brainly.com/question/11536910
#SPJ1
List all of the integer values that could take that would satisfy the inequality shown on the number line below.

Answers
Answer:
-2 ; -1 ; 0 ; 1
Step-by-step explanation:
the inequality is satisfied in this interval [-2.5,1].
We are searching the integers: -2 ; -1 ; 0 ; 1
All the values of x that satisfy the inequality will be;
⇒ x = - 2, - 1, 0, 1
What is Inequality?
A relation by which we can compare two or more mathematical expression is called an inequality.
Given that;
The inequality is given.
Now,
The solution of the inequality are given as;
⇒ x ∈ [- 2.5, 1]
But we can find the integers which satisfy the inequality.
Hence, All the values of x that satisfy the inequality will be;
⇒ x = - 2, - 1, 0, 1
Thus, All the values of x that satisfy the inequality will be;
⇒ x = - 2, - 1, 0, 1
Learn more about the inequality visit:
https://brainly.com/question/25275758
#SPJ2
I need help! I don’t understand!

Answers
Answer:
33
Step-by-step explanation:
just coint how much is on each side then multiply it by 3
PLz help i dont want to fail

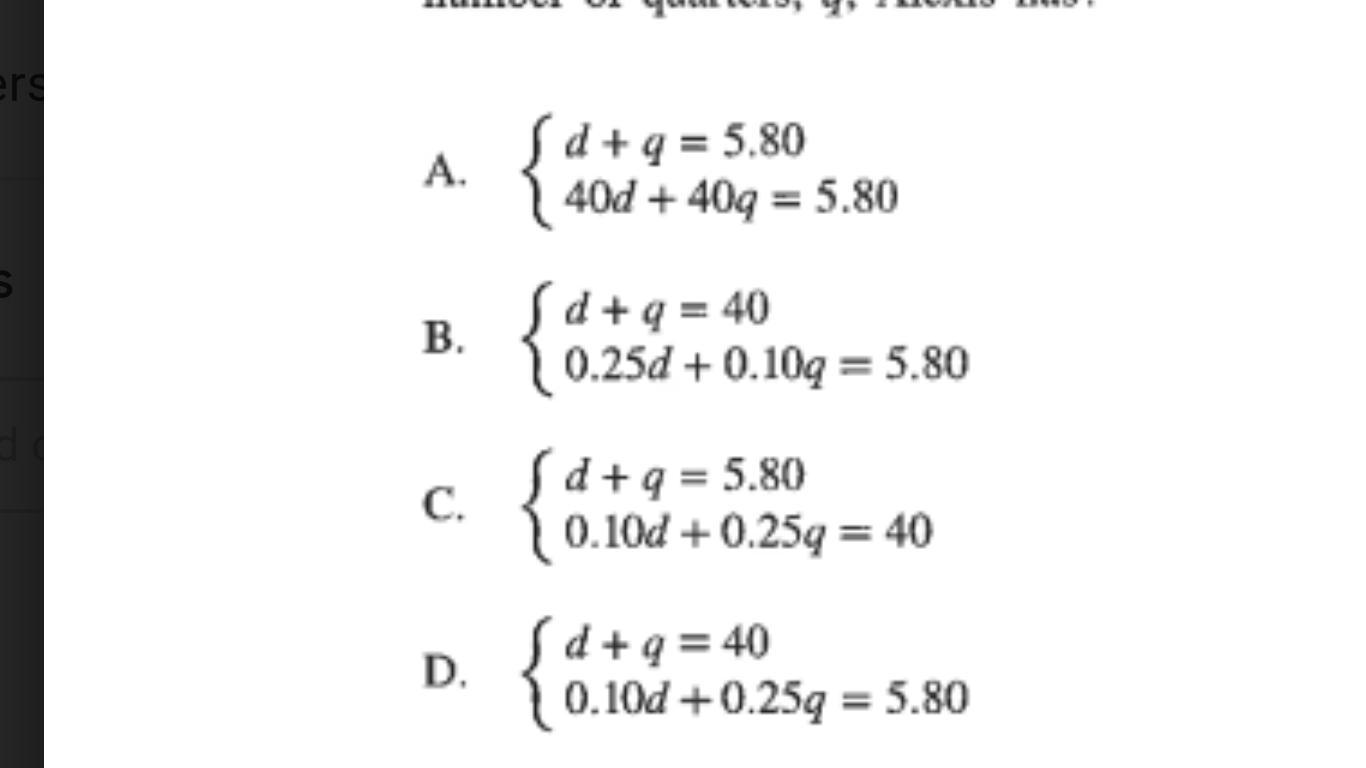
Answers
Answer:
D
Step-by-step explanation:
5x2.36 x+36 = 0
Which value of x is a solution to this equation
Answers
Answer:
x = -3.05
Step-by-step explanation:
(5×2.36)x + 36 = 0
11.8x + 36 = 0
(118/10) x + 36 = 0
118x + 360 = 0 × 10
118x = -360
x = -360/118
x = -180/59 ( -3.05)
The final exam grade of a statistics class has a skewed distribution with mean of 81. 2 and standard deviation of 6. 95. If a random sample of 42 students selected from this class, then what is the probability that the average final exam grade of this sample is between 75 and 80?
Answers
The probability that the average final exam grade of the sample is between 75 and 80 is approximately 0.294, or 29.4%.
To solve this problem, we need to calculate the z-scores for the lower and upper bounds of the average final exam grade range, and then use the z-scores to find the corresponding probabilities from the standard normal distribution.
First, let's calculate the z-score for the lower bound:
z1 = (75 - 81.2) / (6.95 / sqrt(42))
z1 = -6.2 / (6.95 / sqrt(42))
z1 ≈ -2.512
Next, let's calculate the z-score for the upper bound:
z2 = (80 - 81.2) / (6.95 / sqrt(42))
z2 = -1.2 / (6.95 / sqrt(42))
z2 ≈ -0.528
Now, we can use the z-scores to find the corresponding probabilities using a standard normal distribution table or a calculator.
The probability that the average final exam grade of the sample is between 75 and 80 is equal to the probability of having a z-score between z1 and z2.
P(z1 < Z < z2) = P(-2.512 < Z < -0.528)
By looking up the probabilities corresponding to these z-scores from a standard normal distribution table or using a calculator, we find:
P(-2.512 < Z < -0.528) ≈ 0.294
Know more about probability here;
https://brainly.com/question/31828911
#SPJ11
can anyone help please????

Answers
Answer:
Option A. \((f_of^{-1})(-2)=-2\)
Step-by-step explanation:
Point to remember while solving the question of function,
\((f_of^{-1})(x)=x\)
Here, 'f' is the parent function and \(f^{-1}\) is the inverse of the function 'f'.
So for the given function,
f(x) = 2x - 2
\((f_of^{-1})(x)=x\)
For x = -2
\((f_of^{-1})(-2)=(-2)\)
Therefore, Option A will be the correct answer.
What is the size of x when the opposite is 4.9 the hypotenuse is 7.2 i need to work out x which is where it meets with the hypotenuse and adjacent?
Answers
Answer:
Step-by-step explanation:
10
1. Find the derivative of the following function. Write your
answer in the simplest form. (3 marks)
f(x) = x^2e^−5x
2. A farmer wants to fence in a rectangular plot of land
adjacent to the south wal
Answers
The derivative of \(f(x) = x^2e^{(-5x)\) is:
\(f'(x) = 2xe^{(-5x)} - 5x^2e^{(-5x)\)
What is derivative?In mathematics, a quantity's instantaneous rate of change with respect to another is referred to as its derivative. Investigating the fluctuating nature of an amount is beneficial.
To find the derivative of the given function, we apply the product rule.
The product rule states that if we have a function f(x) = g(x) * h(x), where g(x) and h(x) are both differentiable functions, then the derivative of f(x) is given by f'(x) = g'(x) * h(x) + g(x) * h'(x).
In this case, g(x) = x² and h(x) = \(e^{(-5x)\). Taking the derivatives of g(x) and h(x), we get g'(x) = 2x and h'(x) = \(-5e^{(-5x)\).
Applying the product rule, we have:
f'(x) = g'(x) * h(x) + g(x) * h'(x)
\(= 2x * e^{(-5x)} + x^2 * (-5e^{(-5x)})\)
\(= 2xe^{(-5x)} - 5x^2e^{(-5x)\)
Therefore, the derivative of \(f(x) = x^2e^{(-5x)\) is \(f'(x) = 2xe^{(-5x)} - 5x^2e^{(-5x)}.\)
To learn more about derivative here:
https://brainly.com/question/29144258
#SPJ4
Raina's penny bank is 1/4 full. After she adds 360 pennies, it is 5/8 full. How many pennies can Raina's bank hold?
Answers
Answer:
960
Step-by-step explanation:
We start with the variable "x". Let's call "x" Raina's penny bank.
After adding 360 pennies, at the end, she has 5/8x, or 5/8.
So we start with
(1/4)x + 360 = 5/8x
Let's subtract 1/4x from both sides
360 = 5/8x - 1/4x
Remember, we need to use common denominators to subtract, so 1/4 becomes 2/8
360 = 5/8x - 2/8x
Now we simplify to get
360=3/8x
Multiply the reciprocal of 3/8 to both sides which is 8/3
360 * 8/3 = x
Answer is 960 pennies.
Therefore Raina's bank hold 960 pennies.
Answer:
we need to get the same number below to make it easier. so 1/4 will be equal to 2/8.
then she adds 360 pennies so it's 5/8 full.
therefore, the 360 pennies = 3/8 full
because 5/8 - 2/8 = 3/8.
now, we need to divide 360/3 so we can get how much pennies when it's 1/8 full.
360 pennies/3 = 120 pennies = 1/8 full.
now to get a full bank we just need to multiply 120 x 8 because 1/8 x 8 = 1 which means a full fraction.
120 pennies x 8 = 960 pennies.
Raina's bank can hold up to 960 pennies.
