The slope and Y-Intercept for y=-x+2
Answers
Answer:
1 and 2
Step-by-step explanation:
slope is 1
y intercept is 2
basically base it off the equation y = mx + b
the m is the slope, but since in this case there is no number before x, you just put 1, since 1 times x is just x and thats why its left out
the b is the y intercept, so in this case its 2
Related Questions
Three times a number increased by ten to equal to twenty less than six times the number. Find the number.
PLEASE HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
will mark brainlist.
Answers
Answer:
x =10
Step-by-step explanation:
3x + 10 = 6x -20
3x - 6x + 10 = -20
-3x + 10 = -20
-3x = -20 -10
-3x = -30
x = -30/-3
x = 10
Check:
3(10) + 10 = 6(10) - 20
30 + 10 = 60 - 20
40 = 40
(2x +9x^2 - 4x +10)/ (x+5)
Answers
Answer:
9x^2 - 2x + 10 / x +5
Step-by-step explanation:
I was not sure what you meant so I simplified it C:
Answer:
9x2−2x+10/x+5
this is simplified
If f(x) = 3x-6 and g(x) = 1/3x+1, then (g(f))^-1 (x) equals.
1-x
1/3(3x-1)
(x+1)
(x-1)
Answers
We need to find the inverse of the function gof (x). First we need to find the composite function gof (x) which is given by:
\(g(f(x)) = g(3x - 6)\)
= \((1/3)(3x - 6) + 1\)
= x - 1 + 1
= x
Thus,
gof (x) = x.
Now we need to find the inverse of the function gof (x) to obtain
\((gof)^-1 (x).\)
We have gof (x) = x
which implies\((gof)^-1 (x)\)
= gof (x)^-1
= x^-1
= 1/x,
x ≠ 0
Therefore,
\((gof)^-1 (x) = 1/x\)
which is option (3) (x+1) since 1/x can be written as 1/(x+1-1), where (x+1-1) is the denominator of 1/x.
Hence, the correct option is (3).
To know more about two functions visit:
https://brainly.com/question/19517220
#SPJ11
To find (g(f))^-1 (x), substitute the expression for f(x) into g(x) and simplify. The composition of g(f) is x and its inverse is also x. Therefore, (g(f))^-1 (x) equals x.
Explanation:To find (g(f))^-1 (x), we need to first find the composition of g(f) and then find its inverse. Start by substituting the expression for f(x) into g(x): g(f(x)) = g(3x-6) = \frac{1}{3}(3x-6) + 1 = x - 1 + 1 = x. So, g(f(x)) = x. Now, to find the inverse of g(f), we switch the x and y variables and solve for y: y = x. Therefore, (g(f))^-1 (x) = x.
Learn more about Composition of Functions here:https://brainly.com/question/33783470
#SPJ12
Which of the following is a requirement for a random sample? a Every individual has an equal chance of being selected. b The probabilities cannot change during a series of selections. c There must be sampling with replacement d All of the other 3 choices are correct.
Answers
The correct answer is a: every individual has an equal chance of being selected. A random sample is a subset of a population that is selected in a way that each member of the population has an equal probability of being chosen.
The randomness of the sample helps to ensure that the results obtained from the sample are representative of the entire population.
Option b, the probabilities cannot change during a series of selections, is a requirement for independent events but not necessarily for a random sample.
Option c, there must be sampling with replacement, is not always required for a random sample. Sampling with replacement means that after an individual is selected, they are returned to the population and can be selected again. This is not always necessary for a random sample.
Therefore, the correct answer is a: every individual has an equal chance of being selected.
To know more about random sample, visit the link given below:
https://brainly.com/question/29107208
#SPJ4
A ball has a mass of 140 g. What is the force needed to accelerate the ball at 25m/s 2
Answers
Answer:
3.5N
Step-by-step explanation:
140g=0.14kg
F=ma
F=0.14×25
F=3.5N
Which of these statements is true? Check all that apply. CDs have a higher mean than digital. The range of digital is 800. The median of CDs is 400. Both have the same interquartile range. Both have the same median. Digital's mean is around 467.
Answers
Bar chart associated with the question is attached below
Answer:
Range of digital is 800
CDs have a higher mean than digital
Digital's mean is around 467.
Both have the same interquartile range
Step-by-step explanation:
CDs have a mean higher than digital
Range of digital is 800 (900 - 100 = 800)
Both have the same interquartile range
(Q3 - Q1)
DIGITAL :
(900+700+500+300+300+100)
700 - 300= 400
CDs:
(1000+800+800+600+400+200)
800 - 400= 400
Digital mean :
(900+700+500+300+300+100) / 6
2800/6 = 466.67 = 467
CD mean :
(1000+800+800+600+400+200) /6
=633.333
Median of CD:
1000+800+800+600+400+200
(800+600)/ 2 = 700
Median of Digital :
(500+300)/2 = 400

Answer:
A: CDs have a higher mean than digital.
B: The range of digital is 800.
D: Both have the same interquartile range.
F: Digital’s mean is around 467.
Step-by-step explanation:
edg2020

Determine when, to the nearest year, $5,000 invested at 5% per year, compounded daily, will be worth $10,000.
____ yr
Answers
To the nearest year, $5,000 invested at 5% per year, compounded daily, will be worth $10,000 in approximately 14 years.
To determine the time it takes for the investment to double, we can use the compound interest formula: A = P(1 + r/n)^(n*t), where A is the future value, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years.
In this case, the principal amount (P) is $5,000, the annual interest rate (r) is 5% (or 0.05), and the investment is compounded daily, so the number of times interest is compounded per year (n) is 365. We want to find the number of years (t) it takes for the investment to reach $10,000.
Setting up the equation: 10,000 = 5,000(1 + 0.05/365)^(365*t), we can solve for t using logarithms or trial and error. The result is approximately 14 years. Therefore, it will take approximately 14 years for the $5,000 investment to grow to $10,000 at a 5% annual interest rate, compounded daily.
Learn more about compound interest formula
https://brainly.com/question/29639856
#SPJ11
the lenth of rectangle exceeds its breath by 9 cm if the lenght and breath increased by 3cm area of new rectangle will be 84^2cm more than that of the given rectangle, find the lenght & breath of the given rectangle
Answers
The length and breadth of the given rectangle is 17 cm and 8 cm, respectively.
Let's suppose the breadth of the given rectangle is 'b' cm.
So, the length of the rectangle will be '(b+9)'.
According to the problem, if we increase the length and breadth by 3 cm each, then the area of the new rectangle will be 84 sq cm more than the given rectangle.
Area of the given rectangle = lb = (b+9)b = b²+9b
Area of the new rectangle = (l+3)(b+3)
Area of new rectangle = lb + 3l + 3b + 9 [Since lb = area of the given rectangle]
Area of new rectangle = (b²+9b) + 3(b+9) + 3b + 9
Area of new rectangle = b² + 15b + 36
Let's consider the difference in area of the new rectangle and the given rectangle:
84 sq cm = (b²+15b+36) - (b²+9b)84 sq cm = 6b+3684 sq cm - 36 = 6b84 sq cm - 36 = 6b48 = 6bb = 8 cm
Therefore, the length of the rectangle will be '8+9=17 cm'.
To know more about area please visit :
https://brainly.com/question/25292087
#SPJ11
In a random sample of citizens in one town, 21 out of 200 people were left handed. Which of these is the best inference to
make?
Answers
Answer:
A about ten percent of the town is left handed
Step-by-step explanation:
20 of 200 is ten percent and this town could be an outlier in left handed populations.
vanya walks late at night along a straight street of length l, lit by n lanterns. consider the coordinate system with the beginning of the street corresponding to the point 0, and its end corresponding to the point l. then the i-th lantern is at the point ai. the lantern lights all points of the street that are at the distance of at most d from it, where d is some positive number, common for all lanterns. vanya wonders: what is the minimum light radius d should the lanterns have to light the whole street?
Answers
The minimum light radius d for the lanterns to light the whole street is the maximum distance between any two lanterns.
The minimum light radius d needed for the lanterns to light the whole street is the maximum distance between any two lanterns. To find this, first we need to calculate the distance between each pair of lanterns. This can be done by subtracting the coordinate of the first lantern from the coordinate of the second lantern. After calculating the distances between each pair of lanterns, we need to find the maximum distance of these. This maximum distance is the minimum light radius d needed to light the whole street. Thus, we can conclude that the minimum light radius d should be equal to the maximum distance between any two lanterns.
Learn more about minimum here
https://brainly.com/question/29499469
#SPJ4
Please help me! I will give brainliest if right

Answers
A company finds that on average, they use 43 minutes for each meeting.
An employee sketches a graph to show the total amount of time in minutes, T, used for m meetings. The graph shows the value of T for 1 to 5 meetings.
If the employee counts by 10's, what should be the largest value on the T-axis of his or her graph so that the scale is the most appropriate for the given information?
Answers
The largest value on the T-axis of his or her graph so that the scale is the most appropriate for the given information is 220.
How to plot a graph?Plotting a graph involves visually representing numerical data using a coordinate system. The following steps can be used as a general guide to plot a graph:
1. Determine the type of graph needed: There are different types of graphs such as line graphs, bar graphs, pie charts, etc. The type of graph you choose will depend on the nature of the data being represented.
2. Choose a scale: This involves selecting appropriate values for the x and y-axes of the graph. The scale should allow the data to be displayed clearly, and evenly spaced marks should be used to represent values.
3. Plot the data: Mark the points or bars representing the data on the graph, using the selected scale.
4. Label the axes: Label both the x and y-axes with a description of what each represents, and include units of measurement where applicable.
5. Title the graph: Give the graph a descriptive title that indicates the purpose of the graph.
6. Add any necessary details: Additional details such as a legend, data source, or notes can be included to provide further information about the data or the graph.
7. Review and revise: Check the graph to ensure that it accurately represents the data and is visually clear. Make any necessary revisions to improve the graph's effectiveness.
To determine the largest value on the T-axis of the graph, we need to first find the maximum possible value of T for the given information.
Since the average time used for each meeting is 43 minutes, the total time used for m meetings can be expressed as T = 43m.
To find the maximum value of T for 5 meetings, we substitute m = 5 into the equation:
T = 43(5) = 215
Therefore, the largest value on the T-axis should be slightly larger than 215 to provide a little bit of extra space on the graph.
If the employee counts by 10's, a good choice for the largest value on the T-axis would be 220. This would allow for the values of T for 1 to 5 meetings to be evenly spaced on the graph, with each mark on the T-axis representing 10 minutes of time.
To learn more about graphs visit:
brainly.com/question/17267403
#SPJ1
PLEASE HELP ILL GIVE BRAINLIEST
SHOW YOUR WORK

Answers
in humans, a widow's peak is dominant to having a straight hairline, and free earlobes are odminant to having attached ones. a woman who is homozygous for her widow's peak and heterozygous for her earlobes marries a man that has a straight hairline and is also heterozygous for his earlobes. determine the phenotypic ratio. what is the probability that they have a child who looks like mom?
Answers
The phenotypic ratio is 4:2:2:0, or 2:1:1:0. and the probability that they have a child who looks like mom is 9/16
The woman is homozygous for her widow's peak, which means that she has two dominant alleles (W). She is heterozygous for her earlobes, which means that she has one dominant allele (F) and one recessive allele (f). The man has a straight hairline, which means that he has two recessive alleles (w), and he is heterozygous for his earlobes (Ff).
To determine the phenotypic ratio of their offspring, we can use a Punnett square to combine the alleles of the parents. The Punnett square for this cross is:
W w
F W₁ w₁
f W₂ w₂
The possible genotypes of the offspring are WW₁₁, WW₁₂, Ww₁₁, Ww₁₂, ww₁₁, ww₁₂, and we can use the rules of dominance to determine the corresponding phenotypes:
Widow's peak and free earlobes (WW₁₁, WW₁₂, Ww₁₁, Ww₁₂): 4/4 = 100%
Widow's peak and attached earlobes (Ww₂₂, WW₂₂): 2/4 = 50%
Straight hairline and free earlobes (ww₁₁, ww₁₂): 2/4 = 50%
Straight hairline and attached earlobes (ww₂₂): 0/4 = 0%
Therefore, the phenotypic ratio is 4:2:2:0, or 2:1:1:0.
To find the probability that they have a child who looks like the mother (widow's peak and free earlobes), we need to consider the possible genotypes of the offspring that have at least one dominant allele for both traits. These are WW₁₁, WW₁₂, Ww₁₁, and Ww₁f₂
Therefore, the probability of having a child who looks like the mother is:
P(Widow's peak and free earlobes) = 4/4 + 2/4 + 2/4 + 1/4 = 9/16
In conclusion, the Punnett square can help us determine the possible genotypes and corresponding phenotypes of offspring from a cross between parents with known genotypes.
To learn more about probability click on,
https://brainly.com/question/13916726
#SPJ4
Find the amount to which $800 will grow under each of these conditions: a. 8% compounded annually for 9 years. Do not round intermediate calculations. Round your answer to the nearest cent. $ b. 8% compounded semiannually for 9 years. Do not round intermediate calculations. Round your answer to the nearest cent. $ C. 8% compounded quarterly for 9 years. Do not round intermediate calculations. Round your answer to the nearest cent. d. 8% compounded monthly for 9 years. Do not round intermediate calculations. Round your answer to the nearest cent. $ e. 8% compounded daily for 9 years. Assume 365-days in a year. Do not round intermediate calculations. Round your answer to the nearest cent. $ f. Why does the observed pattern of FVs occur?
Answers
The amount to which $800 will grow under each of the given conditions increases as the compounding period decreases.
The amount to which $800 will grow under each of these conditions is as follows:a) 8% compounded annually for 9 years
When compounded annually for 9 years at 8%, the formula is: Amount = Principal x [(1 + rate/n)^(n*t)]
Where: Principal = $800 Rate = 8% Time = 9 years
Compounded annually = n = 1 Amount = $1,447.91 (rounded to the nearest cent)
b) 8% compounded semiannually for 9 years Compounded semiannually for 9 years at 8%, the formula is:
Amount = Principal x [(1 + rate/n)^(n*t)]
Where: Principal = $800 Rate = 8% Time = 9 years Compounded semiannually = n = 2 Amount = $1,471.16 (rounded to the nearest cent)
c) 8% compounded quarterly for 9 years Compounded quarterly for 9 years at 8%, the formula is:
Amount = Principal x [(1 + rate/n)^(n*t)]
Where: Principal = $800 Rate = 8% Time = 9 years Compounded quarterly = n = 4 Amount = $1,491.03 (rounded to the nearest cent)
d) 8% compounded monthly for 9 years Compounded monthly for 9 years at 8%, the formula is: Amount = Principal x [(1 + rate/n)^(n*t)]
Where: Principal = $800 Rate = 8% Time = 9 years Compounded monthly = n = 12 Amount = $1,505.91 (rounded to the nearest cent)
e) 8% compounded daily for 9 years Compounded daily for 9 years at 8%, the formula is:
Amount = Principal x [(1 + rate/n)^(n*t)]
Where: Principal = $800 Rate = 8% Time = 9 years Compounded daily = n = 365Amount = $1,511.74 (rounded to the nearest cent)
The observed pattern of FVs (future values) occurs due to compounding. Compounding is the process of earning interest not only on the principal amount invested but also on the interest earned from the principal. This results in an increase in the interest earned and the future value of the investment. The more frequent the compounding, the higher the future value of the investment. Hence, the amount to which $800 will grow under each of the given conditions increases as the compounding period decreases.
To learn more about compound follow the given link
https://brainly.com/question/14782984
#SPJ11
What equation corresponds with the situation?
Story 1: Lin had 90 flyers to hang up around the school.
She gave 12 flyers to each of three volunteers. Then
she took the remaining flyers and divided them up
equally between the three volunteers.
Story 2: Lin had 90 flyers to hang up around the school.
After giving the same number of flyers to each of three
volunteers, she had 12 left to hang up by herself.
Write an equation corresponding to each story.
+ 12
Story A
Story B
3(12 + y) = 90
Answers
Answer:
Story 1
Step-by-step explanation:
For story 1:
Lin gave 12 flyers to 3 people. She took the remaining flyers (90 - (12*3)) and divided then into groups of 3 to give to the volunteers. That would be 3(12) + 3(y) = 90 which is also 3(12+y) = 90.
For story 2:
The equation would be "3(y) + 12 = 90" and not "3(12+y) = 90"
Using powers of 10, which would be the best choice for the first number to subtract in the division problem 956 87?
87
8,700
870
800
Answers
Answer:
the second one
Step-by-step explanation:
Answer:
87, I believe. The powers of 10, and 87 is in the powers of 10.
Step-by-step explanation:
Please help, i know you have to use pythagoras and the hypotenuse is 8.44 but i dont know how to get one of the sides

Answers
======================================================
Explanation:
Check out the diagram below.
I've defined the following points:
A = center of the circle, and center of the squareB, C, D, and E = vertices of the square that are on the circleF = midpoint of segment CDNow focus on triangle ACF. This is an isosceles right triangle with legs of 0.5x each. The hypotenuse is the radius of the circle. Let R be that unknown radius.
The area of the circle is given to us. It is 56 square cm. Use this to find the value of R.
\(A = \pi*(\text{radius})^2\\\\56 = \pi*R^2\\\\R^2 = 56/\pi\\\\R = \sqrt{56/\pi}\\\\R = 4.22200825\\\\\)
This value is approximate. I used the calculator's stored version of pi to get the most accuracy possible.
------------
We now know the hypotenuse of triangle ACF.
Use Pythagoras (aka Pythagorean Theorem) to have the following steps:
\(a^2+b^2 = c^2\\\\(0.5\text{x})^2+(0.5\text{x})^2 = 4.22200825^2\\\\0.25\text{x}^2+0.25\text{x}^2 = 17.82535366\\\\0.5\text{x}^2 = 17.82535366\\\\\text{x}^2 = 17.82535366/0.5\\\\\text{x}^2 = 35.65070732\\\\\text{x} = \sqrt{35.65070732}\\\\\text{x} = 5.97082132708726\\\\\text{x} = 5.97\\\\\)
The final answer is 5.97With the exception of 0.5 and 0.25, each decimal value mentioned is approximate.
Keep in mind that rounding to 3 sig figs means that we're rounding to 2 decimal places. The units digit is 1 sig fig, and the 2 decimal places give a total of 1+2 = 3 sig figs.
In short, we're rounding to the nearest hundredth.
--------------------
Check:
x = 5.97 is the square's side length.
It divides in half to get x/2 = 5.97/2 = 2.985 which gives each leg of triangle ACF.
Use a = 2.985 and b = 2.985 in the Pythagorean Theorem to find that c = 4.22142748 approximately. This is the approximate radius of the circle.
Use that radius to find the area of the circle.
A = pi*r^2
A = pi*(4.22142748)^2
A = 55.984594705958
A = 56.0
I'm rounding the area to 3 sig figs to keep consistent with the rounding done to x. We arrive at the circle area of 56 square cm, which helps confirm the answer is correct.

please help please please please please please please please please please please please please please please please please please please please please please please please please please please please please please please please please please please please

Answers
part 1 of the question is asking us to evaluate expressions to the power of 2. To do that let's remember the following:
\(a^2=a\times a\)Ther is, when a number is elevated to second power it means we have to multiply that number by itself. For example:
\(\begin{gathered} 1^2=1\times1=1 \\ 2^2=2\times2=4 \\ 3^2=3\times3=9 \end{gathered}\)In the second part of this question, we are asked to evaluate the square root of a number. Let's remember that the square root is the inverse operation of elevating a number to the second power. That is if we have:
\(\sqrt[]{a}=b\)it means:
\(b^2=b\times b=a\)For example:
\(\begin{gathered} \sqrt[]{1}=1 \\ \sqrt[]{4}=2 \\ \sqrt[]{9}=3 \end{gathered}\)The third part of the questions asks us to solve for "x" the following equation:
\(x^2=9\)To do that we take square root on both sides:
\(\sqrt[]{x^2}=\sqrt[]{9}\)Since the square root of a number to the second power is the same number and the square root of 9 is 3, we get:
\(x=3\)f(x) = 3x + 2
What is f(5)?
Answers
Answer:
17
Step-by-step explanation:
Substitute 5 in place of x
f(5) = 3*5 + 2
Assume you have a poker chip set containing blue, red, and white chips, all of the same size. This time, you place 18 blue chips, 23 red chips, and 9 white chips in a bag. Using the Law of Large Numbers, what is the probability of selecting a red chip from the bag?
Answers
Impulse, change in momentum, final speed, and momentum are all related concepts in the context of Newton's laws of motion. Let's go through each option and explain their relationships:
(a) Impulse delivered: Impulse is defined as the change in momentum of an object and is equal to the force applied to the object multiplied by the time interval over which the force acts.
Mathematically, impulse (J) can be expressed as J = F Δt, where F represents the net force applied and Δt represents the time interval. In this case, you mentioned that the net force acting on the crates is shown in the diagram. The impulse delivered to each crate would depend on the magnitude and direction of the net force acting on it.
(b) Change in momentum: Change in momentum (Δp) refers to the difference between the final momentum and initial momentum of an object. Mathematically, it can be expressed as Δp = p_final - p_initial. If the crates start from rest, the initial momentum would be zero, and the change in momentum would be equal to the final momentum. The change in momentum of each crate would be determined by the impulse delivered to it.
(c) Final speed: The final speed of an object is the magnitude of its velocity at the end of a given time interval.
It can be calculated by dividing the final momentum of the object by its mass. If the mass of the crates is provided, the final speed can be determined using the final momentum obtained in part (b).
(d) Momentum in 3 s: Momentum (p) is the product of an object's mass and velocity. In this case, the momentum in 3 seconds would be the product of the mass of the crate and its final speed obtained in part (c).
To rank these quantities from greatest to least for each crate, you would need to consider the specific values of the net force, mass, and any other relevant information provided in the diagram or problem statement.
Learn more about Momentum here:
https://brainly.com/question/24030570
#SPJ11
3x +y = -5
2x + 3y = -8
Answers
Answer:
Step-by-step explanation:
for 3x +y = -5
it's \(x = \frac{-5 -y}{3}\)
and for 2x + 3y = -8 it's
\(x = \frac{-8 - 3y}{2}\)
Solve the equation:5(3+6a)=-15+6(5+5a)
Answers
Answer:
0.5Step-by-step explanation:
To solve the equation 5(3+6a) = -15+6(5+5a), we need to use the rules of algebra to isolate the variable "a" on one side of the equation and simplify the other side.
First, we can distribute the 5 on the left side of the equation to obtain 53 + 56a = -15+6(5+5a). This gives us 15 + 30a = -15+6(5+5a).
Next, we can distribute the 6 on the right side of the equation to obtain 15 + 30a = -15+65 + 65a. This gives us 15 + 30a = -15+30 + 30a.
Now we can combine like terms on both sides of the equation to obtain 30a = -15 + 30, which simplifies to 30a = 15. Finally, we can divide both sides of the equation by 30 to obtain a = 0.5.
Therefore, the solution to the equation 5(3+6a) = -15+6(5+5a) is a = 0.5
Find the measure of AB
A. 20
B. 21
C. 22
D. 14

Answers
Answer:
\(CB.CA=CD .CK\)
\(9(9+2x+5)=10(10+2x+1)\)
\(9(2x+14)=10(2x+11)\)
\(18x+126=20x+110\)
\(126-110=20x-18x\)
\(16=2x->x=8\)
\(AB=2(18)+5\)
\(=21\)
So, your answer is B) 21
hope it helps...
Did americans work less than 40 hours a week on average in 1977? in 1977, the gss included questions about the number of hours that the respondent worked per week. The average number of hours worked per week was 34. 61 hours with a standard deviation of 14. 77 hours. A sample of 32 respondents was questioned. Find the test statistic.
Answers
The test statistic is, -2.06.
What is test statistic?
A programme and any related documentation are examined during static testing, a type of software testing that does not call for the programme to be run. Software testing also includes dynamic testing, which involves interacting with the application as it is being used.
Given: Americans work less than 40 hours a week on average in 1977?
In 1977, the GSS included questions about the number of hours that the respondent worked per week.
The average number of hours worked per week was 34. 61 hours with a standard deviation of 14. 77 hours.
A sample of 32 respondents was questioned.
So, the test statistics is,
Z = (x bar - μ)/(σ /√n)
= (34.61 - 40)/(14.77/sqrt(32))
Z = -2.06
Hence, the test statistics is -2.06.
To know more about the test statistic, click on the link
https://brainly.com/question/15980493
#SPJ4
A boy saves up $79 for a gift for his friend. However, upon reaching the store, he realizes that he saved 257% of the actual amount he needed to buy the present. How much does the present cost? Round to the nearest cent.
Hint: This is a Part = Percent × Whole problem.
You're given the part (79) and the percent (257%, or 2.57).
Substitute these into the equation to find the whole.
Answers
Answer:
$30.74
Step-by-step explanation:
Find the local maxima, local minima, and saddle points, if any, for the function z = 3x3 – 36xy – 3y3. (Use symbolic notation and fractions where needed. Give your answer as point coordinates in t
Answers
Answer:
(0,0) is a saddle point
(-4,4) is a local maximum
Step-by-step explanation:
\(\displaystyle z=3x^3-36xy-3y^3\\\\\frac{\partial z}{\partial x}=9x^2-36y\\\\\frac{\partial z}{\partial y}=-36x-9y^2\)
Determine critical points
\(9x^2-36y=0\\9x^2=36y\\\frac{x^2}{4}=y\)
\(-36x-9y^2=0\\-36x-9(\frac{x^2}{4})^2=0\\-36x-\frac{9}{16}x^4=0\\x(-36-\frac{9}{16}x^3)=0\\\\x=0\\\\-36-\frac{9}{16}x^3=0\\-36=\frac{9}{16}x^3\\-64=x^3\\-4=x\)
When x=0
\(9x^2-36y=0\\9(0)^2-36y=0\\-36y=0\\y=0\)
When x=-4
\(9x^2-36y=0\\9(-4)^2-36y=0\\9(16)-36y=0\\144-36y=0\\144=36y\\4=y\)
So, we need to check what kinds of points (0,0) and (-4,4) are.
For (0,0)
\(\displaystyle H=\biggr(\frac{\partial^2 z}{\partial x^2}\biggr)\biggr(\frac{\partial^2 z}{\partial y^2}\biggr)-\biggr(\frac{\partial^2 z}{\partial x\partial y}\biggr)^2\\\\H=(18x)(-18y)-(-36)^2\\\\H=(18(0))(-18(0))-(-36)^2\\\\H=-1296 < 0\)
Therefore, (0,0) is a saddle point since \(H < 0\).
For (-4,4)
\(\displaystyle H=\biggr(\frac{\partial^2 z}{\partial x^2}\biggr)\biggr(\frac{\partial^2 z}{\partial y^2}\biggr)-\biggr(\frac{\partial^2 z}{\partial x\partial y}\biggr)^2\\\\H=(18x)(-18y)-(-36)^2\\\\H=(18(-4))(-18(4))-(-36)^2\\\\H=(-72)(-72)-1296\\\\H=5184-1296\\\\H=3888 > 0\)
Because \(H > 0\) and since \(\frac{\partial^2z}{\partial x^2}=-72 < 0\), then (-4,4) is a local maximum
Solve for y in the two equations below using substitution.
3x - 9y = 9
-2x - 2y = 8

Answers
Answer:
C
Step-by-step explanation:
3x - 9y = 9 → (1)
- 2x +2y = 8 ( subtract 2y from both sides )
- 2x = - 2y + 8 ( divide through by - 2 )
x = y - 4
substitute x = y - 4 into (1)
3(y - 4) - 9y = 9
3y - 12 - 9y = 9
- 6y - 12 = 9 ( add 12 to both sides )
- 6y = 21 ( divide both sides by - 6 )
y = \(\frac{21}{-6}\) = - \(\frac{7}{2}\)
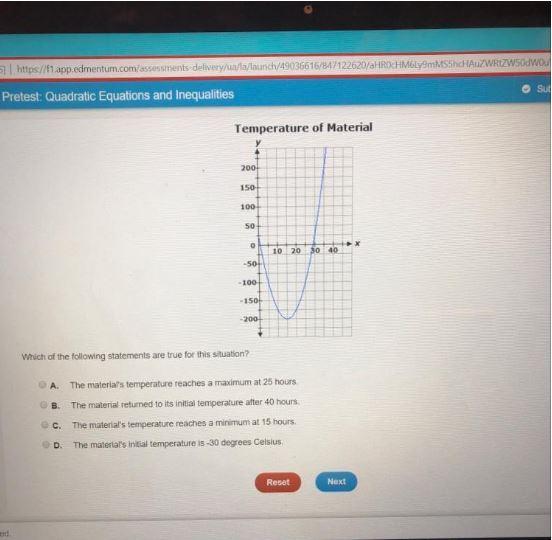
An engineering student is studying the effects of cryogenic treatments on a particular material. The treatment involves cooling the material with specific applications of liquid nitrogen.
The temperature of the material in degrees Celsius, y, can be modeled by the following graph, where x represents the time, in hours, since the treatment began.
Answers
The true statement about the graph from the attached image below is: The material's temperature reaches a minimum at 15 hours.
What is the parabolic graph of the quadratic equation?The parabolic graph is a curved U-shaped graph that is established from a quadratic equation.
The parabola of the graph can be downward creating a maximum or upward (minimum).
From the given image, the correct interpretation shows that as a result of cryogenic treatment, the material's temperature reaches a minimum at 15 hours.
Learn more about parabolic graphs here:
https://brainly.com/question/33428
#SPJ1
If a=21m and c=35m what is the length of side b using the pythagorean
theorem?
28m
28
45