the side of a triangle blowers extended a form and exterior angle of 144 degrees. find a value of x

Answers
A side of a triangle below has been extended a form and exterior angle of 144 degrees. Find a value of x
______________________________
The sum of supplementary angles is 180º
180- 144 = 36º
______________________________________________
Right angle 90 º
_________________________
____________________________
The sum of the angles of a triangle is 180º
180º= 36º + 90º + X
180º - 36º - 90º = X
x= 54º
___________________________
Answer
x= 54º



Related Questions
plss help me !!!!!!!!!!!

Answers
Answer:
\(9 \sqrt{2} \)
Step-by-step explanation:
\(3 \sqrt{6} \times \sqrt{3} \\ 3 \times \sqrt{2} \sqrt{3} \times \sqrt{3} \\ 3 \times 3 \sqrt{2} \\ 9 \sqrt{2} \)
WILL MAKE BRAINLIEST!!!
write the equation given the slope and y-intercept
1.) m= 1, b=2
2.) m= 1/4, b=0
3.) m= -3, b= 0.5
4.) m= 0.2, b=0.8

Answers
2) y=1/4x
3) y=-3x+0.5
4) y=0.2x+0.8
Please help me I wanna get out this class
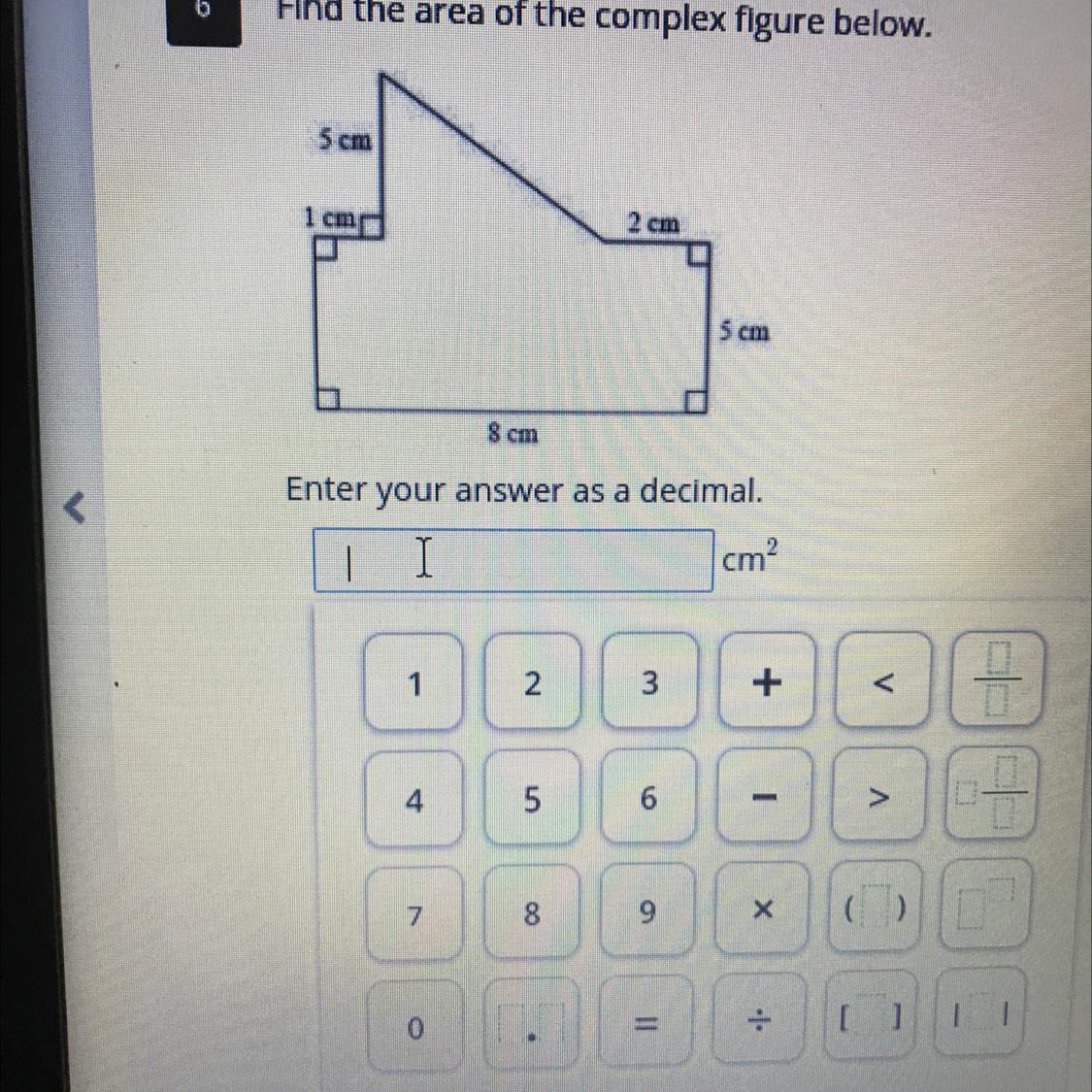
Answers
area of rectangle is length x width
8x5=40
area of triangle is base x height divide by 2
5x5=25
25 divide by 2 is 12.5
add them together
40+12.4 = 52.4
-
13. Marcus works 40 hours per week at a store.
• He earns $8.75 per hour.
• Each week $36 is deducted from his paycheck for taxes.
How much money does Mark earn, after taxes have been deducted,
during a 4-week period?
A $314
B. $386
C. $1,256
D. $1,364
Answers
36*4= 144
1400-144=$1,256 after tax deductions
The total amount of money Mark earns after taxes have been deducted,
during a 4-week period is $1256.
What is the total earnings of Mark?The first step is to detemine his total earnings in 4 weeks:
Total earnings = 4 (earnings per hour x total hour worked per week)
4 x 8.75 x 40 = $1400
The second step is to determine the total taxes for 4 weeks
4 x 36 = $144
Now subtract $144 from $1400
$1400- $144 = $1256
To learn more about taxes, please check: https://brainly.com/question/25311567
Max has 382 baseball cards, Ali has 4x more, how many more does Ali have? What is the total of the cards added together?
Answers
Answer:
Ali has 1528. She has 1146 more cards than Max. In total, there are 1910 cards.
Step-by-step explanation:
382 x 4 = 1528
1528 - 382 = 1146
1528 + 382 = 1910
Answer:
If Max=382 and Ali=4x\(4x = 4 \times 382 = 1448\)total cards added together is 328+1448=2776Select the correct answer.
Select the event that is impossible.
A flipped coin landing heads side up.
Having a birthday on the 32nd March.
Snow in March.

Answers
correct answer is snow in march
Answer:
32nd of March
Step-by-step explanation:
Maximum number of days to ever exist in March is 31. That will not change. The only changing month is February
The chair of the operations management department at Quality University wants to construct a p-chart for determining whether the four faculty teaching the basic P/OM course are in control with regard to the number of students who fail the course. Accordingly, he sampled 100 final grades from last year for each instructor, with the following results: Instructor Number of Failures Prof. A 13 Prof. B 0 Prof. C 11 Prof. D 16 What is the estimate of the standard deviation of the sampling distribution for an instructor's sample proportion of failures?
Answers
Answer:
0.03
Step-by-step explanation:
Given the following :
Instructor __no of failure __prop (failure /100)
A ________ 13__________0.13
B ________0___________0
C________11___________0.11
D________16__________0.16
Prof. B adds no proportion to the data and hence excluded in the estimation.
Mean(m) = 0.13 + 0.11 + 0.16) / 3
= 0.4 / 3
= 0.1333
Standard deviation :
Σ(X - m)² / N - 1
Σ(0.13 - 0.1333)² + (0.11 × 0.1333)² + ( 0.16 - 0.1333)² = 0.0012668689
= 0.0012668689 / 2
= 0.00063343445
√0.00063343445
= 0.0251681
= 0.03 To 2 decimal places
672,829
Word Form
Expanded Form
Unit Form
Answers
Answer and Step-by-step explanation:
The Word form is:
Six hundred, seventy-two thousand, eight hundred and twenty nine.
The Expanded form is:
600,000 + 70,000 + 2,000 + 800 + 20 + 9
The Unit form is:
6 one hundred thousands, 7 ten thousands, 2 thousands, 8 hundreds, 2 tens and 9 ones.
#teamtrees #PAW (Plant And Water)
The equation E = mgh gives the gravitational potential energy of an object, where g is the
acceleration due to gravity, m is the mass of the object, and h is the height of the object.
Solve for h in terms of E, m, and g.
Answers
Step-by-step explanation:
Starting with the equation E = mgh, we can solve for h in terms of E, m, and g as follows:
E = mgh
Divide both sides by mg:
E/mg = h
Therefore, h = E/mg.
So the solution for h in terms of E, m, and g is h = E/mg.
Find the sum of 2.53 x 1019 and 3.197 x 1017.
2.56197 x 1019
3.2223 x 1019
2.56197 x 1036
3.2223 x 1036
Answers
Taking into account the scientific notation, the result of the sum is 2.56197×10¹⁹.
Scientific notationScientific notation is a quick way to represent a number using powers of base ten.
The numbers are written as a product:
a×10ⁿ
where:
a is a real number greater than or equal to 1 and less than 10, to which a decimal point is added after the first digit if it is a non-integer number.n is an integer, which is called an exponent or an order of magnitude. Represents the number of times the comma is shifted. It is always an integer, positive if it is shifted to the left, negative if it is shifted to the right.Sum in scientific notationYou want to add the following two numbers in scientific notation:
2.53×10¹⁹3.197×10¹⁷When the numbers to be added do not have the same base 10 exponent, the base 10 power with the highest exponent must be found. In this case, the highest exponent is 19.
Then all the values are expressed as a function of the base 10 exponent with the highest exponent. In this case: 3.197×10¹⁷= 0.03197×10¹⁹
Taking the quantities to the same exponent, all you have to do is add what was previously called the number "a". In this case:
2.53×10¹⁹ + 0.03197×10¹⁹= (2.53 + 0.03197)×10¹⁹= 2.56197×10¹⁹
Finally, the result of the sum is 2.56197×10¹⁹.
Learn more about sum in scientific notation:
brainly.com/question/11403716
brainly.com/question/853571
#SPJ1
The function f(x)=−3x+2 is defined over the domain −1
Answers
The domain of the function f(x) = -3x + 2 is (-∞, +∞), representing all real numbers, and the range is (-∞, 2], representing all real numbers less than or equal to 2.
The function f(x) = -3x + 2 is a linear function defined by a straight line. To determine the domain of this function, we need to identify the range of values for which the function is defined.
The domain of a linear function is typically all real numbers unless there are any restrictions. In this case, there is no explicit restriction mentioned, so we can assume that the function is defined for all real numbers.
Therefore, the domain of the function f(x) = -3x + 2 is (-∞, +∞), which represents all real numbers.
Now, let's analyze the range of the function. The range of a linear function can be determined by observing the slope of the line. In this case, the slope of the line is -3, which means that as x increases, the function values will decrease.
Since the slope is negative, the range of the function f(x) = -3x + 2 will be all real numbers less than or equal to the y-intercept, which is 2.
Therefore, the range of the function is (-∞, 2] since the function values cannot exceed 2.
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
Please help me?!!!!!!

Answers
Answer:
Bargain Busters shop sells the cheapest soup
Step-by-step explanation:
Bargain Busters sell 4 cans of soup for £3.76
Bargain Busters sell 1 cans of soup for
3.76÷4
=0.94
cost cutters sell 3 cans of soup for £2.85
cost cutters sell 1 cans of soup for 2.85÷3
=0.95
so
Bargain Busters<cost cutters
0.94<0.95
therefore
Bargain Busters shop sells the cheapest soup
Can somebody answer this?

Answers
True
One from of the linear function is Y = mx + b where b is the y intercept.
The y intercept is where x is 0 so it would be at (0,6)
Let σ(n) be the sum of all positive divisors of the integer n and let p be any prime number.
Show that σ(n) < 2n holds true for all n of the form n = p²
Answers
The statement that "σ(n) < 2n holds true for all n of the form n = p²" has been proved.
Let p be any prime number, and let σ(n) be the sum of all positive divisors of the integer n.
As p is a prime number, and 2 is the smallest prime number, so, p\(\geq\)2
So, the positive divisors of the integer n are: 1,p,p².
As σ(n) represents the sum of all positive divisors of the integer n.
σ(n)=1+p+p²
In order to prove that σ(n) < 2n,for all n of the form n = p².
1+p+p²<2p²
p²-p-1>0
It is know that, p\(\geq\)2.
So, p²-p-1\(\geq\)1
Thus, σ(n) < 2n holds true for all n of the form n = p².
Learn more about prime numbers here:
https://brainly.com/question/145452
#SPJ1
(sinx) / (1-cosx) =cscx+cotx
Prove the identity.
Note that each Statement must be based on a Rule chosen from the Rule menu. To see a detailed description of a Rule, select the More Information Button to the right of the Rule.
Answers
\(~~\text{L.H.S}\\\\=\dfrac{\sin x}{1-\cos x}\\\\\\=\dfrac{\sin x(1+ \cos x)}{(1 -\cos x)(1+ \cos x)}\\\\\\=\dfrac{\sin x + \sin x \cos x}{1- \cos^2 x}\\\\\\=\dfrac{\sin x+ \sin x \cos x}{\sin^2 x}\\\\\\=\dfrac{\sin x}{ \sin^2 x}+ \dfrac{\sin x \cos x}{ \sin^2 x}\\\\\\=\dfrac{1}{ \sin x} + \dfrac{\cos x}{ \sin x}\\\\\\=\csc x + \cot x\\\\\\=\text{R.H.S}\\\\\text{Proved.}\)
List the steps that you will do in order to solve for 39 ÷ (12 + 1)− 2 × (4 + 15).
Answers
Answer: -35
1. Simplify 12 + 1 to 13.
39 divided by 13 - 2 (4 + 15)
2. Simplify 4 + 15 to 19.
39 divided by 13 - 2 • 19
3. Simplify 39 divided by 13 to 3.
3 - 2 • 19
4. Simplify 2 • 19 to 38.
3 - 38
5. Simplify.
-35
9514 1404 393
Answer:
simplify parenthesesdivide 39/13multiply 2(19)subtract 3-38Step-by-step explanation:
The order of operations tells you to evaluate parentheses first.
Step 1: simplify (12+1) and (4+15)
39÷13 -2×19
Then it tells you to do multiplication and division, left to right.
Step 2: divide 39÷13
3 -2×19
Step 3: multiply 2×19
3 -38
Finally, addition and subtraction are done, left to right.
Step 4: subtract 38 from 3
-35
HELP!!!! PLEASE NO LINK SCAM THO
Which graph shows all natural numbers less than 3?
OA)
-4 -3 -2 -1
+
4
o
1
2
3
+
+
OB) -4 -3 -2 -1
+
2 3
o
1
4
+
+
OC) -4 -3 -2 -1
+ +
2 3 4
o
1
OD)
-4 -3 -2 -1
+ +
+
0 1 2 3 4

Answers
Answer: C
Step-by-step explanation:
Answer:
The Answer Is B
Step-by-step explanation:
QUESTION 4
a) The numbers 3, x, (x + 6) form the first 3 terms of a positive geometric sequence. Find
i)
ii)
the possible value(s) of x
the tenth term of the sequence
5+6 2 marks
[2 marks]
[3 marks]
S
b) Let A =
6 1 1 2
2 3 -1 and B
1-3 1 – 2
-8
3
4.
e
3x1
i)
Write down the inverse of A V
[6 marks]
ii) Find a matrix X such that AX = B ✓
[4 marks]
c) Sketch the graph of the following polynomial and state the domain and the range.
22
f(x) = -(x + 3)(x + 2)(x - 1)3
0
3x3 ARV
ferse
7
15 marks]

Answers
3, x, x+6 are the first 3 terms of G.P
common ratio is x/3=x+6/x
so we cross multiply x×x=3×x+6
ײ= 3x+18 so we have x²-3x-18
(x-6)(x+3)=0
the possible value of x are 6 and -3
b) tenth term of the seauence
first of all the possible sequence are 3, 6, 12 and 3, -3, 3
but we need only the positive GP
so the common ratio of.the GP r is 6/3=2
the 10th term of a GP sequence is ar^10-1=ar^9
where a = first time
3×2^9=3×512=1536
the 10th term is 1536
List five numbers with eight in the ones place
Answers
Answer: 18, 28, 38, 48, 58
Step-by-step explanation:
Answer:
18, 28, 38, 48, 58
Step-by-step explanation:
I think this is pretty self explanatory.
yis inversely proportional to the square of x.
A table of values for x and y is shown.
a) Express y in terms of x.
b) Work out the positive value of x when y = 25
Answers
Answer:
(a) \(y = \frac{4}{x^2}\)
(b) \(x = \frac{2}{5}\)
Step-by-step explanation:
Given
Variation: Inverse proportional.
This is represented as:
\(y\ \alpha\ \frac{1}{x^2}\)
See attachment for table
Solving (a):
First convert variation to equation
\(y = k\frac{1}{x^2}\)
From the table:
\((x,y) = (1,4)\)
So, we have:
\(4 = k * \frac{1}{1^2}\)
\(4 = k * \frac{1}{1}\)
\(4 = k * 1\)
\(4 = k\)
\(k = 4\)
Substitute 4 for k in \(y = k\frac{1}{x^2}\)
\(y = 4 * \frac{1}{x^2}\)
\(y = \frac{4}{x^2}\)
Solving (b): x when y = 25.
Substitute 25 for y in \(y = \frac{4}{x^2}\)
\(25 = \frac{4}{x^2}\)
Cross Multiply
\(25 * x^2 = 4\)
Divide through by 25
\(x^2 = \frac{4}{25}\)
Take positive square roots of both sides
\(x = \sqrt{\frac{4}{25}\)
\(x = \frac{2}{5}\)

Solve the following linear programming problem. Maximize: z = 7x + 2y subject to: 7x-y≤ 16 2x+y≥ 10 X≥2 y≤9 The maximum value is
Answers
Answer:
To solve the linear programming problem, we need to first graph the feasible region determined by the constraints, and then evaluate the objective function at each corner point of the feasible region to find the maximum value of z.
Plotting the lines corresponding to the inequalities, we get:
Graph of the feasible region:
The feasible region is the shaded polygon in the graph. We can see that the vertices of the feasible region are (2, 9), (2, 12), (4, 7), and (8, 2).
Next, we evaluate the objective function at each of these vertices to find the maximum value of z.
At (2, 9): z = 7x + 2y = 7(2) + 2(9) = 23
At (2, 12): z = 7x + 2y = 7(2) + 2(12) = 31
At (4, 7): z = 7x + 2y = 7(4) + 2(7) = 35
At (8, 2): z = 7x + 2y = 7(8) + 2(2) = 58
Therefore, the maximum value of z is 58, which occurs at the point (8, 2).
Hence, the answer is: the maximum value of z is 58.
Find the height of the tower using the information given in the illustration.

Answers
using SOH CAH TOA
Tan 85.144 =h/130
h=tan 85.144*130
h=1530.19 fr

help please
A car was valued at $42,000 in the year 1994. The value depreciated to $11,000 by the year 2006.
A) What was the annual rate of change between 1994 and 2006?
r=------------ Round the rate of decrease to 4 decimal places.
B) What is the correct answer to part A written in percentage form?
r=------------%
C) Assume that the car value continues to drop by the same percentage. What will the value be in the year 2010 ?
value=$---------------- Round to the nearest 50 dollars.
Answers
(A) Between 1995 and 2003, there was a change at an annual rate of -0.1463
(B) Between 1995 and 2003, a change occurred at a rate of -14.63% per year.
(C) The automobile would be worth $5,844.24 in 2007.
What is depreciation?Depreciation is an annual income tax deduction that enables you to recoup the purchase price or other basis of a specific item over the course of its use.
It is a provision for the property's normal wear and tear, degeneration, or obsolescence.
As the years pass, the car's value drops.
This process is known as depreciation.
Depreciation is the decrease in asset value brought on by normal wear and tear.
Use this formula to calculate the annual rate of change:
g = (FV/PV)¹⁾ⁿ - 1
Now, using the formula calculate as follows:
(11000/3900)¹⁾⁸ - 1
-0.1463 = -14.63%
The following formula can be used to estimate a car's worth in 7 years:
FV = P (1 + g)ⁿ
$39,000 x (1 - 0.1463)¹²
$39,000 x 0.8537¹² = $5,844.24
Therefore, (A) between 1995 and 2003, there was a change at an annual rate of -0.1463
(B) Between 1995 and 2003, a change occurred at a rate of -14.63% per year.
(C) The automobile would be worth $5,844.24 in 2007.
Know more about depreciation here:
https://brainly.com/question/1203926
#SPJ1
Correct question:
A car was valued at $39,000 in the year 1995. The value depreciated to $11,000 by the year 2003.
A)What was the annual rate of change between 1995 and 2003? (Round to 4 decimal places)
B)What is the correct answer to part A written in percentage form?
C)Assume that the car value continues to drop by the same percentage. What will the value be in the year 2007?
The table describes the quadratic function h(x).
x h(x)
−3 −2
−2 −3
−1 −2
0 1
1 6
2 13
3 22
What is the equation of h(x) in vertex form?
h(x) = (x + 2)2 − 3
h(x) = (x + 1)2 − 2
h(x) = (x − 1)2 + 2
h(x) = (x − 2)2 + 3
Answers
The quadratic equation that describes the function is
f(x) = x² + 4x + 1
What is a quadratic equation?A quadratic equation is a equation that is of the form -
y = f{x} = ax² + bx + c
Given is the table that describes the quadratic function h(x) as follows -
{x} h{x}
−3 −2
−2 −3
−1 −2
0 1
1 6
2 13
3 22
The quadratic equation is of the form given -
y = ax² + bx + c
For the point (0, 1), we can write -
1 = c ..... Eq{1}
For the point (1, 6), we can write -
6 = a + b + 1
a + b = 5 ...... Eq{2}
For the point (2, 13), we can write -
13 = 4a + 2b + 1
4a + 2b = 12 ...... Eq{3}
From Eq{2}, we can write -
a = 5 - b
So, the equation 3 can be written as -
4(5 - b) + 2b = 12
20 - 4b + 2b = 12
20 - 2b = 12
2b = 8
b = 4 ...... Eq{4}
then
a = 1 ...... Eq{5}
So, we can write the quadratic equation as -
f(x) = x² + 4x + 1
Therefore, the quadratic equation that describes the function is
f(x) = x² + 4x + 1
To solve more questions on quadratic equations, visit the link below -
brainly.com/question/22412845
#SPJ1
Given: 5(2x-4)=10
Prove: x=3
Drag the correct reason to the box.

Answers
After simplifying an equation the value of x is x = 3.
What is solving an equation?
Unifying Principle for Equation Solving
By deleting parenthesis and grouping like terms, each side of the equation can be made simpler.
The variable term on one side of the equation can be separated using addition or subtraction.
To find the variable, use multiplication or division.
Consider, the given equation
5(2x - 4) = 10
10x - 20 = 10 Removing parenthesis
10x -20 + 20 = 10 + 20 Adding 20 on both sides
10x = 30 Simplifying
x = 3 Dividing both sides by 10
Hence, the value of x is, x = 3.
To know more about solving an equation, click on the link
https://brainly.com/question/22688504
#SPJ1
Discrete Mathematics
For each language L1 to L5, described below, you need to do the following:
• Create a regular expression that defines the language accurately.
The alphabet A = {a, b} will be used.
The languages are:
1. L1 which has exactly one a but any number of bs.
2. L2 which has an odd number of as and an even number of bs.
3. L3 which contains exactly two as or exactly two bs, although not necessarily adjacent.
4. L4 which has all the bs appearing before any of the as, or all the as appearing before any of the bs.
5. L5 where there can be any number of as but the number of bs must be even, although the bs do not have to be adjacent.
Answers
Note: ^ is for Start of the line, $ is for end of the line ,* means 0 or more, + means 1 or more, [ab] means either a or b and {} is for specific number of times, () is for grouping.
How to create regular expressions?A task in which it is necessary to create regular expressions to define five different languages. The alphabet used is A = {a, b}. The languages are:
L1, which has exactly one "a" but any number of "bs".
L2, which has an odd number of "as" and an even number of "bs".
L3, which contains exactly two "as" or exactly two "bs", although not necessarily adjacent.
L4, which has all "bs" appearing before any "a" or all "as" appearing before any "b".
L5, where there can be any number of "as", but the number of "bs" must be even, although the "bs" need not be adjacent.
Learn more about languages in brainly.com/question/20921887
#SPJ1
4/5 • 5/4 = 1 Determine the property illustrated.
Answers
The algebraic property illustrated is the commutative property of multiplication
What are the properties of algebra?
The properties of algebra are those properties mostly used in simplifying algebraic expressions.
Algebraic properties are:
Commutative property of additionCommutative property of multiplicationAssociative property of additionAssociative property of multiplicationDistributive Properties of Addition Over MultiplicationFrom the expression given we have
4/5 • 5/4 = 1
= 4/ 5 × 5/ 4
= 1
Thus, the algebraic property illustrated is the commutative property of multiplication
Learn more about algebraic property here:
https://brainly.com/question/855307
#SPJ1
To create a confidence interval from a bootstrap distribution using percentiles, we keep the middle values and chop off a certain percent from each tail.
(a) What percent of values must be chopped off from each tail for a 95% confidence interval?
(b) If the bootstrap distribution contains values for 1000 bootstrap samples, how many should be chopped off at each end to produce a 95% confidence interval?
Answers
Answer:
a
\(\frac{\alpha }{2} = 2.5 \%\)
b
\(N = 25\)
Step-by-step explanation:
From the question we are told that
The number of bootstrap samples is n = 1000
From the question we are told the confidence level is 95% , hence the level of significance is
\(\alpha = (100 - 95 ) \%\)
=> \(\alpha = 0.05\)
Generally the percentage of values that must be chopped off from each tail for a 95% confidence interval is mathematically evaluated as
\(\frac{\alpha }{2} = \frac{0.05}{2} = 0.025 = 2.5 \%\)
=> \(\frac{\alpha }{2} = 2.5 \%\)
Generally the number of the bootstrap sample that must be chopped off to produce a 95% confidence interval is
\(N = 1000 * \frac{\alpha }{2}\)
=> \(N = 1000 * 0.025\)
=> \(N = 25\)
Answer:
Step-by-step explanation:
Hey
Which of the following inequality’s matches the graph? A: x ≤ 5 B: x ≥ 5 C: y ≤ 5 D: y ≥ 5 what is the answer

Answers
Answer: Choice A
\(x \le 5\)
========================================
Explanation:
Any point in the shaded purple region has an x coordinate that is 5 or smaller. So we go for \(x \le 5\). Either x = 5 or x < 5. The boundary line is solid to indicate that points on the boundary are included in the solution set.
Write the answer without using exponents? -9^3
Answers
Answer:
1/729
Step-by-step explanation:
a negative exponent is fractioned like 1/9^3. Which can be simplified as 1/729 ans 9^3 = 729