Answers
Answer:
c
Step-by-step explanation:
the scale is balanced so its equal
Related Questions
DO THE MATH: Skipper has a credit card account that charges 19% APR using 31
day billing periods. On the first day of the billing period, Skipper buys marine-grade
rope for $933 on the credit card. No other purchases are made. Skipper pays off the
purchase on day 31 at the end of the billing period. What is Skipper's finance
charge? Round your answer to the nearest penny.
Purchase
Day Description
1
Marine-grade rope
Payment
4
Amount
$933.00
Day Amount
31 $933.00
The table below will help you calculate the finance charge.
Answers
Skipper's finance charge at the end of the billing period is given as follows:
$14.77.
How to obtain the finance charge?The finance charge is obtained using simple interest, as there is a simple compounding per year for the debt, and the charge is the amount of interest accrued during the period of one month.
The amount of interest accrued after t years, using simple interest, is given as follows:
I(t) = Prt.
The parameters for the equation are given as follows:
P is the principal.r is the interest rate, as a decimal.t is the time, in years.Considering a period of one month = 1/12 of an year, the values of these parameters for this problem are given as follows:
P = 933, r = 0.19, t = 1/12.
Hence the finance charge for Skipper's purchase is calculated as follows:
I = 933 x 0.19 x 1/12 = $14.77.
(rounding to the nearest penny = nearest cent).
More can be learned about simple interest at https://brainly.com/question/20690803
#SPJ1
Explain how to determine whether two quantities are proportional.
please help :)
Answers
Answer:
* Ratios are proportional if they represent the same relationship.
*If the reduced fractions are the same, your ratios are proportional.
*If two ratios are proportional is to write them as fractions and then reduce them.
Hope its helpful
Thank you
15 POINTS IF U ANSWER

Answers
Answer:
we need explaining of this question
Consider the line which passes through the point P(-5, 1, 4), and which is parallel to the line x=1+7t,y=2+1t,z=3+7t Find the point of intersection of
Answers
Question:
Consider the line which passes through the point P(-5, 1, 4), and which is parallel to the line x=1+7t,y=2+1t,z=3+7t. Find the point of intersection of this new line with each of the coordinate planes: xy-plane, xz-plane and yz-plane.
Answer:
The line intersects the xy plane at (-3, \(\frac{11}{7}\), 0)
The line intersects the xz plane at (-13, 0, -11)
The line intersects the yz plane at (0, \(\frac{13}{7}\), 2)
Step-by-step explanation:
Vector form of a line can be written as;
r(t) = r₀ + vt
Where;
r₀ = position vector of the point where the line passes through
v = direction or slope vector of the line.
From the question, we have a line passing through the point P(-5, 1, 4). This means that;
r₀ = (-5, 1, 4)
Also, the line is parallel to another line with parametric equations:
x=1+7t ------------------(i)
y=2+1t ----------------(ii)
z=3+7t ---------------(iii)
Since the first line is parallel to the second line, then their gradient or slope vector must be the same. This means that;
v = (7, 1, 7) [which are the coefficients of t in the parametric equations]
Therefore, the first line can be written as;
r(t) = (-5, 1, 4) + (7, 1, 7)t
Now, to get the point of intersection of this line with each of the coordinates;
(i) The line will intersect the the xy plane when z = 0
Substitute z = 0 into equation (iii)
0 = 3 + 7t
t = \(\frac{-3}{7}\)
Now substitute t = \(\frac{-3}{7}\) into equation(i)
x = 1 + 7(\(\frac{-3}{7}\))
x = -3
Also, substitute t = \(\frac{-3}{7}\) into equation (ii)
y = 2 + 1(\(\frac{-3}{7}\))
y = \(\frac{11}{7}\)
Therefore, the line intersects the xy plane at (-3, \(\frac{11}{7}\), 0)
(ii) The line will intersect the xz plance when y = 0
Substitute y = 0 into equation (ii)
0 = 2 + 1t
t = -2
Now substitute t = -2 into equation(i)
x = 1 + 7(-2)
x = 1 - 14
x = -13
Also, substitute t = -2 into equation (iii)
z = 3 + 7(-2)
z = 3 - 14
z = -11
Therefore, the line intersects the xz plane at (-13, 0, -11)
(iii) The line will intersect the yz plane when x = 0
Substitute x = 0 into equation (i)
0 = 1 + 7t
t = \(\frac{-1}{7}\)
Now substitute t = \(\frac{-1}{7}\) into equation(ii)
y = 2 + 1(\(\frac{-1}{7}\))
y = \(\frac{13}{7}\)
Also, substitute t = \(\frac{-1}{7}\) into equation (iii)
z = 3 + 7(\(\frac{-1}{7}\))
z = 3 - 1
z = 2
Therefore, the line intersects the yz plane at (0, \(\frac{13}{7}\), 2)
Mrs. Cook is a teacher whose salary is $23,125 for a 185-day school year. In Mrs. Cook's school district, substitute teachers are paid at a rate of $90 per day. If a substitute is paid to teach Mrs. Cook's class in her absence one day, how much less does the school district pay in salary by paying a substitute teacher instead of paying Mrs. Cook for that day? *

Answers
Answer:
$90
Step-by-step explanation:
Off course the school district will pay in salary by $90 less.
What is the equivalent ratio for 4
Answers
The equivalent ratios are 8: 6 and 12:9.
Equivalent ratios:Two ratios are equivalent if they represent the same proportion or relative size. To find an equivalent ratio, we can multiply both terms of the ratio by the same non-zero number. This doesn't change the condition between the two terms.
Here we have 4:3
To find equivalent ratios, we can multiply both terms by the same number.
Multiplying by 2
=> 4 × 2 : 3 × 2
=> 8 : 6
Multiplying by 3
=> 4 × 3 : 3 × 3
=> 12: 9
Therefore,
The equivalent ratios are 8: 6 and 12:9.
Learn more about Equivalent ratios at
https://brainly.com/question/29250986
#SPJ1
Complete Question
What is the equivalent ratio for 4: 3
Which equation has a constant of proportionality equal to 1
Answers
Answer:
Step-by-step explanation:
Is in
Here are four fractions. Write them small to large
2/3
3/5
5/8
7/11
Answers
Answer:
1. 3/5 2. 5/8 3. 7/11 4. 2/3
Step-by-step explanation:
Answer:
Step-by-step explanation:
Here are four fractions. Write them small to large 2/3 3/5 5/8 7/11
11+11 = 22
Line ac and df are parallel they are cut by transversal Hj with your partner find the seven unknown angle measures in the diagram explain your reasoning. What do you notice about the angles with vertex B and the angles with vertex E
Answers
The measure of the unknown angles in the parallel lines AC and DF with transversal HJ are as follow,
m ∠DEH = 63° , m ∠BEF = 63° ,m ∠CBJ = 63°, m ∠CBE = 117° , m ∠FEH = 117° , m ∠BED = 117° , and m ∠ABJ = 117°.
Two lines AC and DF are parallel to each other in the attached figure
Transversal HJ cut lines AC and DF at point B and E respectively.
Measure of ∠ABE = 63°.
Using the result based on corresponding angles, alternate interior angles , and vertically opposite angles of a parallel lines we get,
Measure of ∠ABE ≅ Measure of ∠DEH ( corresponding angles)
⇒Measure of ∠DEH = 63°
Measure of ∠ABE ≅ Measure of ∠BEF ( alternate interior angles)
⇒Measure of ∠BEF = 63°
Measure of ∠ABE ≅ Measure of ∠CBJ ( vertically opposite angles)
⇒Measure of ∠CBJ = 63°
Using the result of linear pair angles,
Measure of ∠ABE + Measure of ∠CBE = 180°
⇒ Measure of ∠CBE = 180° -63°
⇒ Measure of ∠CBE = 117°
Measure of ∠CBE ≅ Measure of ∠FEH ( corresponding angles)
⇒Measure of ∠FEH = 117°
Measure of ∠CBE ≅ Measure of ∠BED ( alternate interior angles)
⇒Measure of ∠BED = 117°
Measure of ∠CBE ≅ Measure of ∠ABJ ( vertically opposite angles)
⇒Measure of ∠ABJ = 117°
Therefore, the measure of the seven unknown angles formed in the parallel line are given by m ∠DEH = 63° , m ∠BEF = 63° ,m ∠CBJ = 63°, m ∠CBE = 117° , m ∠FEH = 117° , m ∠BED = 117° , and m ∠ABJ = 117°.
learn more about parallel lines here
brainly.com/question/18828966
#SPJ1
The above question is incomplete, the complete question is:
Lines AC and DF are parallel. They are cut by transversal HJ with your partner find the seven unknown angle measures in the diagram explain your reasoning. What do you notice about the angles with vertex B and the angles with vertex E.
In the attached figure.

The recommended dosage of a drug for pediatric patients is 200 mg per kilogram of a patient's weight. If Janine weighs 102 lb, how much of the drug should she receive? Use the fact that 1 lb = 0.45 kg
Janine should receive about ____ milligrams of the drug.
(Round to the nearest milligram as needed.)
Answers
Answer: 9180 mg
Step-by-step explanation:
First we must convert the patients weight from lb to kg.
102lb x \(\frac{0.45kg}{1lb}\) = 102 x 0.45 kg = 45.9 kg
Now to calculate the amount of the drug she should receive.
45.9 kg x \(\frac{200mg}{kg}\) = 9180 mg
[~S & (R V S) ] ≡ (Q ⊃ S) where A = T, S = F, R = F, Q = T
Answers
[~S & (R V S)] ≡ (Q ⊃ S) is true when A = T, S = F, R = F, and Q = T by substituting the propositional variables.
What is truth table?A truth table is a table used to determine the truth values of a compound proposition, which is a logical statement made up of simpler propositions using logical operators such as "and" (represented by "&"), "or" (represented by "V"), "not" (represented by "~"), conditional (represented by "⊃"), and biconditional (represented by "≡").
According to question:Let's substitute the given truth values for the propositional variables in the given statement:
[~F & (F V F)] ≡ (T ⊃ F)
Using the truth table for conjunction (represented by "&") and disjunction (represented by "V"), we can simplify the left-hand side of the equivalence:
[T & F] ≡ (T ⊃ F)
Using the truth table for conditional (represented by "⊃"), we can simplify the right-hand side of the equivalence:
F ≡ F
Since both sides of the equivalence have the same truth value, the statement is true.
Therefore, [~S & (R V S)] ≡ (Q ⊃ S) is true when A = T, S = F, R = F, and Q = T.
Learn more about truth table visit:
https://brainly.com/question/29155453
#SPJ1
61. The 2003 Statistical Abstract of the United States reported the percentage of people 18 years of age and older who smoke. Suppose that a study designed to collect new data on smokers and nonsmokers uses a preliminary estimate of the proportion who smoke of .30. a. How large a sample should be taken to estimate the proportion of smokers in the population with a margin of error of .02
Answers
Answer: Required minimum sample size = 2017
Step-by-step explanation:
Formula : Sample size(n) for population proportion(p):
\(n= p(1-p)(\frac{Z^c}{E})^2\) , where E = Margin of error
If p = proportion of smokers
Given: p =0.30 and E=0.02
\(z^c\) for 95% confidence level = 1.96
So,
\(n=0.30(1-0.30)(\dfrac{1.96}{0.02})^2\\\=0.30(0.70)(98)^2\\\\=2016.84\approx2017\)
Hence, required minimum sample size = 2017
Morganton Company makes one product and it provided the following information to help prepare the master budget:
The budgeted selling price per unit is $60. Budgeted unit sales for June, July, August, and September are 8,600, 17,000, 19,000, and 20,000 units, respectively. All sales are on credit.
Thirty percent of credit sales are collected in the month of the sale and 70% in the following month.
The ending finished goods inventory equals 25% of the following month’s unit sales.
The ending raw materials inventory equals 10% of the following month’s raw materials production needs. Each unit of finished goods requires 5 pounds of raw materials. The raw materials cost $2.40 per pound.
Thirty five percent of raw materials purchases are paid for in the month of purchase and 65% in the following month.
The direct labor wage rate is $14 per hour. Each unit of finished goods requires two direct labor-hours.
The variable selling and administrative expense per unit sold is $1.80. The fixed selling and administrative expense per month is $67,000.
5. If 96,250 pounds of raw materials are needed to meet production in August, how many pounds of raw materials should be purchased in July?
Answers
Raw materials purchases in July - Payment for raw materials purchases in July = Desired ending raw materials inventory for July
X pounds - 0.35 * X pounds = 9,500 pounds
Solving this equation will give us the value of X, which represents the pounds of raw materials that should be purchased in July.
To determine the number of pounds of raw materials that should be purchased in July, we need to calculate the raw materials production needs for August and then consider the inventory policies given in the information provided.
Each unit of finished goods requires 5 pounds of raw materials. The budgeted unit sales for August are 19,000 units. Therefore, the raw materials production needs for August would be 19,000 units multiplied by 5 pounds per unit, which equals 95,000 pounds.
The ending raw materials inventory equals 10% of the following month’s raw materials production needs. Therefore, the desired ending raw materials inventory for July would be 10% of 95,000 pounds, which is 9,500 pounds.
To calculate the raw materials purchases for July, we need to consider the payment terms provided. Thirty-five percent of raw materials purchases are paid for in the month of purchase and 65% in the following month.
Let's assume the raw materials purchases for July are X pounds. Then the payment for 35% of X pounds will be made in July, and the payment for 65% of X pounds will be made in August.
The payment for raw materials purchases in July (35% of X pounds) will be:
0.35 * X pounds
The payment for raw materials purchases in August (65% of X pounds) will be:
0.65 * X pounds
Since the raw materials purchases for July should cover the desired ending raw materials inventory for July (9,500 pounds), we can set up the following equation:
Raw materials purchases in July - Payment for raw materials purchases in July = Desired ending raw materials inventory for July
X pounds - 0.35 * X pounds = 9,500 pounds
Solving this equation will give us the value of X, which represents the pounds of raw materials that should be purchased in July.
for such more question on equation
#SPJ8
Khali has a box with the dimensions shown. He plans to cover the box with glitter What is the total surface area to be covered with glitter? Show your work

Answers
Answer:
162
Step-by-step explanation:
4.5x9x4
M Question 2 Unit 7 Chapter 10 %
https://ezto.mheducation.com/ext/map/index.html?
Account for 63859...Pay your trash bills...
Unit 7 Chapter 10 Quiz
2
Imported from inte...
Wait time
Inspection time
Process time
Seved
New folder
Imported from inte....
17 days
13 days
23 days
22 days
12 days
Navern Corporation manufactures and sells custom home elevators. From the time an order is
placed until the time the elevator is installed in the customer's home averages 87 days. This 87
days is spent as follows:
Help
Move time
Queue time
What is Navern's manufacturing cycle efficiency (MCE) for its elevators?
Seve & Exit
Su
Answers
Navern's manufacturing cycle efficiency (MCE) for its elevators is: 41.4%
How to solve the manufacturing cycle efficiencyThe formula for obtaining the manufacturing cycle efficiency is value-added time divided by the production cycle time * 100. In the data given, the process and inspection times qualify as a value-added time
Process time = 23 days
Inspection time = 13 days
Value added time = 23 + 13 = 36days
The production cycle time = Move time + process time + queue time + inspection time + wait time
= 22 + 12 + 23 + 13 + 17 days
= 87 days
So, the manufacturing efficiency time = 36/87 * 100
= 41.4%
Learn more about manufacturing efficiency here:
https://brainly.com/question/29645032
#SPJ1
Find the value of x.
A. 65
B. 32.5
C. 118
D. 130

Answers
Answer:
D. 130
Step-by-step explanation:
The lines are tangent to the circle therefore 90º which makes 65º + 25º. The small triangle with C is iso so the angle of C would be 130 and equivalent to x
Answer:
\(D.\ \ 130\)
Step-by-step explanation:
1. Approach
Refer to the attached diagram of the figure for further explanation. In this problem, one is asked to solve for the degree measure of arc (x). The easiest method to do so is to use the triangle (CAB). One can solve for the measure of angle (<CBA) by using the tangent to radius theorem. Then one can solve for the measure of angle (CAB) by using the base angles theorem. Then one can use the sum of angles in a triangle theorem to solve for angle (<BCA). Finally, one can use the central angles theorem to solve for the arc (x).
2. Find the measure of angles in the triangle
A. Find the measure of angle (<CBE)
As per the given image, lines (BE) and (AE) are tangent. This means that they intersect the circle at exactly one point. A radius is the distance from the center of a circle to the circumference or outer edge of a circle. All radii in a single circle are congruent. The radius of tangent theorem states that, when a tangent intersects a circle at a point of tangency, and a radius also intersects the point of tangency, the angle between the radius and the tangent is a right angle. One can apply this here by stating the following:
\(m<CBE = 90\)
Express angle (<CBE) as the sum of two other angles:
\(m<CBE = m<CBA + m<ABE\)
Substitute with the given and found information:
\(m<CBE = m<CBA + m<ABE\)
\(90 = m<CBA + 65\)
Inverse operations,
\(90 = m<CBA + 65\)
\(25= m<CBA\)
B. FInd the measure of angle (<CAB)
As stated above all radii in a single circle are congruent. This means that lines (CB) and (CA) are equal. Therefore, the triangle (CAB) is an isosceles triangle. One property of an isosceles triangle is the base angles theorem, this theorem states that the angles opposite the congruent sides of an isosceles triangle are congruent. Applying this theorem to the given problem, one can state the following:
\(m<CBA = m<CAB = 25\)
C. Find the measure of angle (<ACB)
The sum of angles in any triangle is (180) degrees. One can apply this theorem here to the given triangle by adding up all of the angles and setting the result equal to (180) degrees. This is shown in the following equation:
\(m<CAB + m<CBA + m<ACB = 180\)
Substitute,
\(m<CAB + m<CBA + m<ACB = 180\)
\(25 + 25 + m<ACB = 180\)
Simplify,
\(25 + 25 + m<ACB = 180\)
\(50 + m<ACB = 180\)
Inverse operations,
\(50 + m<ACB = 180\)
\(m<ACB = 130\)
3. Find the measure of arc (x)
The central angles theorem states that when an angle has its vertex on the center of the circle, its angle measure is equivalent to the measure of the surrounding arc. Thus, one apply this theorem here by stating the following:
\(m<ACB = (x)\\130 = x\)

find the product in lowest terms 24/18x2/17x34/3
Answers
Answer:
Step-by-step explanation:
To find the product of the given fractions in lowest terms, we can multiply the numerators and denominators together, and then simplify the resulting fraction:
(24/18) * (2/17) * (34/3)
First, we can simplify the fractions by reducing any common factors in the numerators and denominators:
24/18 = (212)/(29) = 12/9 = 4/3
2/17 = 2/17
34/3 = (2*17)/3 = 34/3
Now we can multiply the simplified fractions:
(4/3) * (2/17) * (34/3) = (4234)/(3173) = 272/153
The product of the given fractions in lowest terms is 272/153.
The Sugar Sweet Company is going to transport its sugar to market. It will cost $3500 to rent trucks, and it will cost an additional $150 for each ton of sugar transported. Let C represent the total cost (in dollars), and let S represent the amount of sugar (in tons) transported. Write an equation relating C to S. Then use this equation to find the total cost to transport 17 tons of sugar.
Answers
Answer:
C = $6050
Equation:
To write the equation, we have to remember that C is the total cost, so that means the equation should end in "= C". S is the amount of sugar, so the equation would look something like this:
\(3500+150(S)=C\)
3500 is at the beginning since that is the cost for the trucks, and each ton of sugar costs $150, and that would get multiplied by S amount of sugar, to get the total cost, C.
Solving the equation
To solve the equation when S = 17, we simply have to plug in S as 17 into our equation we wrote above.
\(3500+150(17)=C\)
150 * 17 is 2550, and 3500 + 2550 is 6050, which is C.
Our answer is: C = $6050
Is (7,-6) a solution to this system of equations?
y = 1/7x+ 7
X = 7
yes
no
Answers
If you want to get is
Y=mx+b
Y=1/7x+7
Y=1/7*7+7 Since x=7
Y=1+7 Compute 1/7*7
Y=8
Consider the following sets of sample data:A: $31,100, $25,800, $36,300, $30,200, $30,000, $19,800, $22,300, $22,600, $34,900, $21,700, $36,900, $30,800, $31,700, $37,100B: 3.18, 4.24, 4.27, 4.38, 3.87, 4.75, 3.43, 3.35, 4.16, 4.81, 2.98Step 1 of 2 : For each of the above sets of sample data, calculate the coefficient of variation, CV. Round to one decimal place.
Answers
The coefficient of variation for A is 20.37% and for B is 15.98%.
What is coefficient of variation?
In statistics, the relative standard deviation (RSD), commonly referred to as the coefficient of variation formula (CV), is a standardized way to assess how widely spaced out a probability distribution or frequency distribution is. Lower values of the coefficient of variation indicate that the data is highly stable and less variable.
We know that formula for coefficient of variation is
CV = Standard Deviation / Mean
A. $31,100, $25,800, $36,300, $30,200, $30,000, $19,800, $22,300, $22,600, $34,900, $21,700, $36,900, $30,800, $31,700, $37,100
Mean = 411200 / 14
Mean = $29371.42
Similarly,
Standard Deviation = $5984.52
So,
CV = 5984.52 / 29371.42 * 100
CV = 20.37%
B. 3.18, 4.24, 4.27, 4.38, 3.87, 4.75, 3.43, 3.35, 4.16, 4.81, 2.98
Mean = 43.42 / 11
Mean = $3.94
Similarly,
Standard Deviation = $0.63
So,
CV = 0.63 / 3.94 * 100
CV = 15.98%
Hence, the coefficient of variation for A is 20.37% and for B is 15.98%.
Learn more about coefficient of variation from the given link
https://brainly.com/question/30783938
#SPJ1
If a storage tank is holding 450 litres when it is three quarters full, how much will it contain when it is two thirds?
Answers
Answer:
400 litres
Step-by-step explanation:
what is 88,000 divided by 100
Answers
Answer:
880
Step-by-step explanation:
I hope this answer helps!
G = B. What is the length of CD?
CD = ___

Answers
Answer:
10
Step-by-step explanation:
Since G = B (and 284 + 76 = 360), then FE = CD
6b) (4.NF.B.4.c) One batch of brownies calls for 1 box of brownie mix and the added ingredients of eggs, water an oil. For "cake-like" brownies, 1 batch calls for 3 eggs, 1/4 cup of water and 1/4 cup of oil. How much of each of these ingredients are needed if you are baking 3 batches of brownies? *
Answers
Answer:
9 eggs, 3/4 cup water, 3/4 cups of water
EXPLANATION:so 1/4×3, 3 is 3/1 as a fraction
you just multiply 1/4 and 3/1 first 1×3=3 then 4×1=4 so 3/4
what is the area of the figure

Answers
Answer:
A = 2184 cm²
Step-by-step explanation:
the area (A) of the figure is calculated as
A = \(\frac{1}{2}\) h(b₁ + b₂)
where h is the perpendicular height between the bases b₁ and b₂
here h = 42 , b₁ = 52 , b₂ = 52 , then
A = \(\frac{1}{2}\) × 42 × (52 + 52) = 21 × 104 = 2184 cm²
Answer:
A = 2184 cm2
Step-by-step explanation:
Area of a parallelogram:
\(A = b*h\)
\(b=52,h=42\)
\(A=(42)(52)=2184cm^{2}\)
Hope this helps.
Write and simplify an expression for the volume of a rectangular prism with a length of 7.5 ft, width w ft, and height 4.2 ft. What is the volume if the width is 2 ft.
I will you as a brainliest please help me.
Answers
Answer:
63
Step-by-step explanation:
V=length x width x height.
V= 7.5*2*4.2
V=63
Write and simplify an expression for the volume of a rectangular prism with a length of 7.5 ft, width 2 ft, and height 4.2 ft. What is the volume if the width is 2 ft.
____________________Solution :-Given Information :-Length ➢ 7.5 ftWidth ➢ 2 ftHeight ➢ 4.2 ftTo Find :-The Volume of the rectangular prism Formula Used :-\( \boxed{ \sf{volume \: of \: rectangular \: prism = length \times width \times height}}\)Calculation :-Substituting the values given in the formula, We get,
⇒ Volume of rectangular prism = ( 7.5 × 2 × 4.2 ) ft³
⇒ Volume of rectangular prism = 63 ft³
____________________Final Answer :-Volume of the rectangular prism is 63 ft³
____________________Note :-Please scroll from right to left to see the whole solution.
Need help please thanks
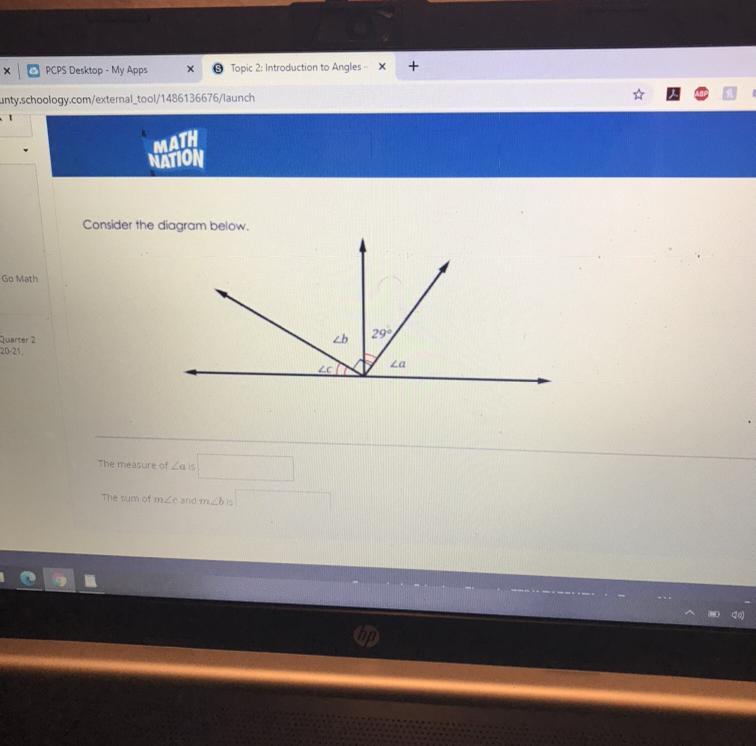
Answers
Answer:
the values of angle;
a=61
b=61
c=29
Answer: All of the angles combined are 180 degrees. Since b and its adjacent angle is 90 degrees, you would subtract 90-29, which gives you 61. b=61. You would then use both angle measures to determine the other two. You would need to find two values that add up to 90 degrees for c and a. Angle b+c would be equal to 90 degrees, and angle a and d (I used d to represent the 29 degree angle) would be equal to 90 degrees, equaling a total of 180 degrees. Angle a would be equal to 61, and angle c would be equal to 29. Hope this helps.
How many gallons of a 50% antifreeze solution must be mixed with 70 gallons of 10% antifreeze to get a mixture that is 40% antifreeze?
Answers
Answer: 180 gallons needed
Step-by-step explanation:
Zykeith,
Assume x gallons of 50% antifreeze is needed
Final mixture is x + 60 gallons
Amount of antifreeze in mixture is 0.4*(x+60)
Amount of antifreeze added is .5x + .1*60 = .5x + 6
so .5x + 6 = .4(x + 60)
.5x -.4x = 24 -6
.1x = 18
x = 180
Let x be the number of gallons of the 50% antifreeze solution needed. We know that the resulting mixture will be 70 + x gallons. To get a 40% antifreeze mixture, we can set up the following equation:
\({\implies 0.5x + 0.1(70) = 0.4(70 + x)}\)
Simplifying the equation:
\(\qquad\implies 0.5x + 7 = 28 + 0.4x\)
\(\qquad\quad\implies 0.1x = 21\)
\(\qquad\qquad\implies \bold{x = 210}\)
\(\therefore\) We need 210 gallons of the 50% antifreeze solution to mix with 70 gallons of 10% antifreeze to get a mixture that is 40% antifreeze.
\(\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}\)
Question: What is the fractional value of A?

Answers
Answer:&.&/
Step-by-step explanation:82
NO LINKS!! Please assist me with this problem Part 1m

Answers
Answer:
(x + 8)² + (y - 8)² = 64=======================
Given ConditionsTangent to x-axis,Tangent to y-axis,In the second quadrant,Radius is 8 units.SolutionEquation of circle:
(x - h)² + (y - k)² = r², where (h, k) is center and r - radiusThe center is the radius long distance from the x- axis to left and y-axis up same distance, this makes it in the second quadrant.
So the coordinates of the center are:
x = - 8, y = 8The equation is:
(x - (-8))² + (y - 8)² = 8²(x + 8)² + (y - 8)² = 64
Answer:
\((x+8)^2+(y-8)^2=64\)
Step-by-step explanation:
Required conditions:
Tangent to both axes.Center in the second quadrant.Radius = 8 units.If the circle is tangent to both axes, its center will be the same distance from both axes. That distance is its radius.
If the center of the circle is in quadrant II, the center will have a negative x-value and a positive y-value → (-x, y).
Therefore, the coordinates of the center will be (0-r, 0+r) where r is the radius.
If the radius is 8 units, then the center is (-8, 8).
\(\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-a)^2+(y-b)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(a, b)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}\)
Substitute the found center and given radius into the formula to create an equation for the circle that satisfies the given conditions:
\(\implies (x-(-8))^2+(y-8)^2=8^2\)
\(\implies (x+8)^2+(y-8)^2=64\)

