The length of a marathon race is 26 miles 385 yards. What is the total length of the marathon race in yards?
Answers
From the equation, it can be deduced that the length of the marathon race will be 47905yards.
Let the total length of the marathon race = x
It should be noted that 1 mile = 1760 yards.
Since the length of a marathon race is 26 miles 385 yards, the conversion in years will be:
x = (26 × 1760) + 385
x = 47520 + 385
x = 47905
Learn more about equations on:
https://brainly.com/question/13763238
Related Questions
Is my work right? Please tell me I’ll give brainliest !!!

Answers
Answer:
Yes Your Work Is correct.
James King
Hope This Helped
Have A Great Day
Answer:
it looks good to me!?
and your hand writing is amazing
Step-by-step explanation:
what is the next 10 numbers of pi?
3.14
Answers
Answer:
3.14159265358
Step-by-step explanation:
Answer:
3.141592653589
Step-by-step explanation:
pi = 3.14159265358979323846264338327950288419716939937510...
Answer: 3.141592653589
Let I be the line given by the span of A basis for L¹ is ={ 3 6 in R³. Find a basis for the orthogonal complement L¹ of L. -5
Answers
Another vector in the orthogonal complement L¹ is C = [0, 0, -15]. The basis for the orthogonal complement L¹ is {B, C} or {[-2, 1, 0], [0, 0, -15]}.
To find a basis for the orthogonal complement L¹ of the line L spanned by the basis vector A = [3, 6] in ℝ³, we need to find vectors that are orthogonal (perpendicular) to every vector in L.
Let's denote a vector in the orthogonal complement as B = [x, y, z]. For B to be orthogonal to A, their dot product must be zero:
A · B = 0
Substituting the values of A and B:
[3, 6] · [x, y, z] = 0
Using the dot product formula:
3x + 6y + 0z = 0
Simplifying the equation:
3x + 6y = 0
Dividing by 3:
x + 2y = 0
Now we have an equation that describes a line in the xy-plane. We can choose any value for y and find the corresponding value for x that satisfies the equation.
Let's choose y = 1. Plugging this into the equation, we have:
x + 2(1) = 0
x + 2 = 0
x = -2
Therefore, one vector in the orthogonal complement L¹ is B = [-2, 1, 0].
To obtain a basis for L¹, we can find another vector that is orthogonal to A and B. One way to do this is by taking the cross product of A and B:
C = A × B
Using the cross product formula:
C = [3, 6, 0] × [-2, 1, 0]
Expanding the cross product:
C = [0, 0, -15]
Therefore, another vector in the orthogonal complement L¹ is C = [0, 0, -15].
The basis for the orthogonal complement L¹ is {B, C} or {[-2, 1, 0], [0, 0, -15]}.
Note that the orthogonal complement is a subspace orthogonal to L, meaning any linear combination of vectors in L¹ will be orthogonal to every vector in L.
Learn more about orthogonal complement here
https://brainly.com/question/19952939
#SPJ11
Consider Jerry's decision to go to college. If he goes to college, he will spend $15,000 on tuition, $12,000 on room and board, and $2,000 on books. If he does not go to college, he will earn $27,000 working in a store and spend $10,000 on room and board. Jerry's cost of going to college is $29,000 $56,000 $46,000 $66,000
Answers
Jerry's cost of going to college is $29,000.
Jerry's cost of going to college is $29,000. The cost of going to college is a major concern for many students. As a result, making a sound financial plan is essential when considering post-secondary education. It is important to weigh the costs of going to college against the benefits of obtaining a degree. Jerry has to make a choice between going to college or working in a store. If he chooses to go to college, he will have to spend $15,000 on tuition, $12,000 on room and board, and $2,000 on books. Therefore, his total cost of attending college is
$29,000 ($15,000 + $12,000 + $2,000).
If he decides not to go to college, Jerry will earn $27,000 by working in a store and spend $10,000 on room and board. By adding up his earnings and expenses, he will have a total of
$17,000 ($27,000 - $10,000)
In this case, it is less expensive for Jerry not to go to college. He will have $12,000 more in his pocket ($17,000 - $29,000) if he does not go to college. Therefore, Jerry's cost of going to college is $29,000.
To know more about financial plan visit:
https://brainly.com/question/29763313
#SPJ11
can anyone tell me the answer to this problem (v-3)^2
Answers
Answer:
v^2 - 6v + 9
Step-by-step explanation:
(v-3)^2 can be written as
(v - 3) (v - 3)
v^2 -3v -3v + 9
v^2 -6v + 9
So, our answer is v^2 -6v + 9
Given are five observations collected in a regression study on two variables:
xi 2 6 9 13 20
yi 7 18 9 26 23
a) Develop a scatter diagram for these data.
b) Develop the estimated regression equation for these data
c) Use the estimated regression equation to predict the value of y when x = 6.
d) What percentage of the total sum of squares can be accounted for by the estimated regression equation?
e) What is the sample correlation coefficient?
f) What is the value of the standard error of the estimate?
g) Test for a significant relationship by using the t test. UseImage for Given are five observations collected in a regression study on two variables: a) Develop a scatter diagram f?=.05.
Answers
The given problem requires developing a scatter diagram, estimating the regression equation, predicting values, determining the percentage of total sum of squares accounted for, calculating the sample correlation coefficient, finding the standard error of the estimate, and conducting a t-test to test for a significant relationship between the variables.
To start, a scatter diagram is constructed by plotting the given data points (xi, yi) on a graph, where xi represents the independent variable and yi represents the dependent variable. This visual representation helps understand the relationship between the variables.
Next, the estimated regression equation is determined by finding the equation of the line that best fits the data. This equation is in the form of y = a + bx, where "a" represents the y-intercept and "b" represents the slope of the line. The equation is obtained through statistical calculations.
Using the estimated regression equation, the value of y can be predicted for a given x. In this case, the prediction is required when x = 6. By substituting this value into the regression equation, the corresponding y-value can be determined.
The percentage of the total sum of squares accounted for by the estimated regression equation is a measure of how well the regression line fits the data. It indicates the proportion of the variation in the dependent variable that can be explained by the independent variable.
The sample correlation coefficient, denoted by r, measures the strength and direction of the linear relationship between the variables. It ranges from -1 to +1, with positive values indicating a positive correlation, negative values indicating a negative correlation, and values close to zero indicating a weak or no correlation.
The standard error of the estimate provides an estimate of the average distance between the observed data points and the regression line. It quantifies the accuracy of predictions made using the regression equation.
Finally, a t-test is conducted to test the significance of the relationship between the variables. This involves determining whether the slope of the regression line is significantly different from zero. The t-test uses a significance level (often denoted as α) of 0.05 to assess the statistical significance of the relationship.
Learn more about statistical here: https://brainly.com/question/29000275
#SPJ11
The opposite of -8/9 is
Answers
Step-by-step explanation:
-9/8 is it's resiprocal
Please show how you got answer

Answers
Here we have -x+y=16
When you take x to other side you must change sign of it
Then y=16+x
Y=x+16
I hope u learn
Question: 4. P(Z < z) = 0.9251 a.) -0.57 b.) 0.98 c.) 0.37 d.) 1.44 e. ) 0.87 1 5
Answers
The value of z that satisfies P(Z < z) = 0.9251 is approximately 1.44(d).
The question asks for the value of z that corresponds to a cumulative probability of 0.9251.The value of z represents the standard score or z-score, which corresponds to a particular cumulative probability.To find this value, we can use a standard normal distribution table or a statistical software.
By looking up the closest probability value in the table, we find that the corresponding z-value is approximately 1.44. Therefore, the answer is option (d) 1.44.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ11
Consider this system of equations.
p=2n
p-5 = 1. 5n
What value of n makes the system of equations true?
Enter your answer in the box.
Answers
Therefore, the value of n that makes the system of equations true is n = 10.
Given:
p = 2n
p - 5 = 1.5n
Substituting the value of p from the first equation into the second equation, we have:
2n - 5 = 1.5n
Next, we can solve for n by subtracting 1.5n from both sides of the equation:
2n - 1.5n - 5 = 0.5n - 5
Simplifying further:
0.5n - 5 = 0
Adding 5 to both sides of the equation:
0.5n = 5
Dividing both sides by 0.5:
n = 10
Therefore, the value of n that makes the system of equations true is n = 10.
Learn more about equations here
https://brainly.com/question/29657992
#SPJ11
Change the Cartesian integral into an equivalent polar integral.l1,1 n(x^2 y^2 1) Then evaluate the polar integral.
Answers
The required polar integral is 0.14173.
To change the Cartesian integral into an equivalent polar integral, we can use the formula:
∫∫R f(x, y) dA = ∫θ₁ θ₂ ∫r₁ r₂ f(r, θ) r dr dθ
Given the Cartesian integral:
∫∫D f(x, y) dA = ∫₁ ₁ ∫₁ ₁ [n(x²y² + 1)] dx dy
We will convert this into a polar integral using the following transformations:
r = √(x² + y²)
θ = tan⁻¹(y/x)
Then, we replace x² + y² with r² and dx dy with r dr dθ.
Substituting r cos θ for x and r sin θ for y, we have:
r = √(x² + y²)
r = √(r² cos²θ + r² sin²θ)
r = √(r²(cos²θ + sin²θ))
r = √(r²) = r
Next, we need to change the limits of integration. The inequality x² + y² ≤ 1 represents a circle centered at the origin with a radius of 1. Thus, the region can be written as:
r cos θ² + r sin θ² ≤ 1
r² ≤ 1
Now we can evaluate the polar integral. Applying the transformation and integrating:
∫∫D f(x, y) dA = ∫₁ ₁ ∫₁ ₁ [n(x²y² + 1)] dx dy
∫∫D f(x, y) dA = ∫₀ ²π ∫₀ ¹ [n(r⁴ cos²θ sin²θ + 1)] r dr dθ
After obtaining the polar integral, we can evaluate it as follows:
Integrating with respect to r:
(r/5 + r³/3) ∣₀¹
Integrating with respect to θ:
(θ/10) ∣₀ π/10
Evaluating these expressions, we find:
0.14173
Learn more about polar integral
https://brainly.com/question/30142438
#SPJ11
A pair of shoes is on sale for $76.50 after a 15% discount was applied. What was the original price of the shoes?.
Answers
The original price of the shoe before the discount was applied is $88
How to calculate the original price the shoe?A pair of shoes is on sale for $76.50
A discount of 15% was applied on the shoe
The original price of the shoe can be calculated as follows
=15/100 × 76.50
= 0.15 × 76.50
= 11.5
= 11.5 + 76.50
= 88
Hence the original price of the shoes before the application of discount is $88
Read more on discount here
https://brainly.com/question/18631484
#SPJ1
Show that the Fundamental Theorem of Algebra must be true for all quadratic polynomial functions.
Answers
we can conclude that the Fundamental Theorem of Algebra must be true for all quadratic polynomial functions.
To show that the Fundamental Theorem of Algebra must be true for all quadratic polynomial functions, we need to demonstrate that every quadratic polynomial function has at least one complex root.
A quadratic polynomial function is of the form f(x) = ax^2 + bx + c, where a, b, and c are coefficients and a ≠ 0.
To find the roots of this quadratic function, we set f(x) equal to zero and solve for x:
ax^2 + bx + c = 0
To solve this quadratic equation, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a)
The discriminant, b^2 - 4ac, determines the nature of the roots. If the discriminant is positive, the quadratic has two distinct real roots. If the discriminant is zero, the quadratic has a repeated real root. And if the discriminant is negative, the quadratic has a pair of complex conjugate roots.
For a quadratic function, the discriminant can be expressed as D = b^2 - 4ac.
Now let's consider the three possible cases:
1. If the discriminant D > 0, then b^2 - 4ac > 0. This indicates that the quadratic equation has two distinct real roots.
2. If the discriminant D = 0, then b^2 - 4ac = 0. This means that the quadratic equation has a repeated real root.
3. If the discriminant D < 0, then b^2 - 4ac < 0. In this case, the quadratic equation does not have real roots. However, according to the Fundamental Theorem of Algebra, every polynomial equation of degree n has exactly n complex roots (counting multiplicity). Since a quadratic polynomial has degree 2, it must have two complex roots, even if they are not real.
Therefore, regardless of the values of a, b, and c in a quadratic polynomial function, the quadratic equation always has at least one complex root, which supports the Fundamental Theorem of Algebra.
Hence, we can conclude that the Fundamental Theorem of Algebra must be true for all quadratic polynomial functions.
To learn more about polynomial click here:
brainly.com/question/8827771
#SPJ11
3x+2=11 what is it ?
Answers
Answer: x = 3
Steps: 3x+2=11
3x + 2 - 2 = 11 - 2
3x = 9
3x/3 = 9/3
x = 3
It’s a linear equation. You can calculate its root through “isolating” the x:
3x = 11 - 2
3x = 9
x = 9/3 = 3
HELP ME PLEASEE!!!! BRAINLIEST FOR CORRECT ANSWER!!!

Answers
Answer: 69
Step-by-step explanation: You divide them into one square and three rectangles, find the area of all the shapes, and add them together, so you get:
9 + 15 + 18 + 27 = 69.
A region in the first quadrant is enclosed by the graphs of y=e 2x
,x=1, and the coordinate axes. If the region is rotated about the y-axis, the volume of the solid that is generated is represented by which of the following integrals? (A) 2π∫ 0
1
xe 2x
dx (B) 2π∫ 0
1
e 2x
dx (C) π∫ 0
1
e 4x
dx (D) π∫ 0
e
ylnydy (E) 4
π
∫ 0
e
ln 2
ydy
Answers
The volume of the solid generated by rotating the region in the first quadrant, enclosed by the graphs of y = e^(2x), x = 1, and the coordinate axes, about the y-axis can be represented by the integral:
(A) 2π∫[0 to 1] x*e^(2x) dx.
To find the volume of the solid, we use the method of cylindrical shells. We integrate the area of each cylindrical shell formed by rotating an infinitesimally thin strip of the region about the y-axis.
In this case, the height of each cylindrical shell is given by the function
y = e^(2x), and the radius is the corresponding x-value.
The limits of integration are from x = 0 to x = 1, as specified by the given region.
Using the formula for the volume of a cylindrical shell, V = 2π * radius * height * thickness, and substituting the height as y = e^(2x) and the radius as x, we get the integral 2π∫[0 to 1] x*e^(2x) dx, which represents the volume of the solid generated.
Therefore, the correct representation for the volume of the solid is option (A) 2π∫[0 to 1] x*e^(2x) dx.
Learn more about volume here:-brainly.com/question/1578538
#SPJ11
AlphaMart sells groceries at the west end of Main Street, a street that is one kilometre long. AlphaMart competes with BetaMarket, which is located at the east end of the street. AlphaMart and BetaMarket sell groceries that are identical in every respect, apart from the locations of the two stores. The marginal cost of an item of groceries is $3 to both retailers. Main Street is home to 200 consumers; the consumers are evenly spaced along the street. Each consumer demands one item of groceries, and faces a travel cost of $12 per kilometre. What price does BetaMarket choose in equilibrium? Hint: Keep a record of your answer for use in later questions.
Answers
If each consumer demands one item of groceries and faces a travel cost of $12 per kilometer. BetaMarket chooses the price of $33.33 in equilibrium.
AlphaMart sells groceries at the west end of Main Street, a street that is one kilometer long. AlphaMart competes with BetaMarket, which is located at the east end of the street. AlphaMart and BetaMarket sell groceries that are identical in every respect, apart from the locations of the two stores. The marginal cost of an item of groceries is $3 for both retailers.
Main Street is home to 200 consumers; the consumers are evenly spaced along the street. Each consumer demands one item of groceries and faces a travel cost of $12 per kilometer. To calculate the equilibrium price of BetaMarket, we first need to find out the quantity demanded at each price point.
The quantity demanded for each price point can be found by subtracting the number of consumers who are closer to AlphaMart than to BetaMarket from the total number of consumers. Let the price charged by BetaMarket be P. If BetaMarket charges P, then the demand for BetaMarket's groceries is given by:
QB = 200/2 - 1/2 (P + 12) = 100 - 1/2 (P + 12)
QB = 100 - 1/2P - 6
We can now write down BetaMarket's profit function as:
πB = QB(P - 3) = (100 - 1/2P - 6)(P - 3)
πB = 100P - 3/2P² - 309
From this, we can find the first-order condition for profit maximization by differentiating the profit function with respect to P and setting it equal to zero:
∂πB/∂P = 100 - 3P = 0P = 100/3
Thus, BetaMarket chooses to set the price at $33.33 in equilibrium.
You can learn more about equilibrium at: brainly.com/question/30694482
#SPJ11
This is the thing that I need help on pls helpppp

Answers
Answer:
144 in^2
Step-by-step explanation:
Using the A = s^2 and the text says that s= 12in
the answer is 12 in * 12 in = 144 in^2
A box contains 9 balls written B,E,R,N,H,E,A,R,T. Two balls are drawn at random without replacement. what is the probability of getting both balls written with R ?
Answers
Answer:
How many balls have “R” written on them initially? We can see this is 2.
How many balls are there initially? This is 9.
As a result, the probability of initially drawing a ball with an R on it is 2/9, as out of the 9 possible draws we could make, 2 of them result in a ball with R on it.
How many balls have “R” written on them now? We can see this is 1, since we just drew one ball with R on it and didn’t replace.
How many balls are there in total right now? This is 8, because we took away one.
As a result, the probability of drawing a ball with an R on it after having already done so is 1/8, as out of the 8 possible draws we could make, 1 results in a ball with R on it.
We then multiply these two values (2/9)*(1/8) = 2/72, which is our probability.
Another way to think about this is that there are 72 possible combinations of balls that we could draw, counting each ball uniquely. This is because of our denominator, since 8*9=72. Out of those 72 outcomes that could possibly happen, 2 outcomes will result in both balls being written with R.
Step-by-step explanation:
what is the ratio of 16 dogs and 12 cats
Answers
ratio of 16 dogs and 12 cats ↓
dogs : cats → 16 : 12
[ simplify both by 4 ]
→ \(\frac{16}{4}\) : \(\frac{12}{4}\)
→ 4 : 3
ratio of dogs : cats = 4 : 3
Solution:
To solve this question, we need to write the ratio in the form of:
(Number of dogs:Number of cats)Then, we need to simplify it to obtain the simplified ratio.
Writing the ratio:
(Number of dogs:Number of cats)=> (16:12)Simplifying the ratio:
(16:12 = 4 x 4:4 x 3)=> 4:3The ratio of 16 dogs and 12 cats is 4:3.
look at picture************^^^^

Answers
i need help with math can any one help
Answers
A) At approximately what production level, q, is profit maximized? B) What is the price of the productC) What are the fixed costs
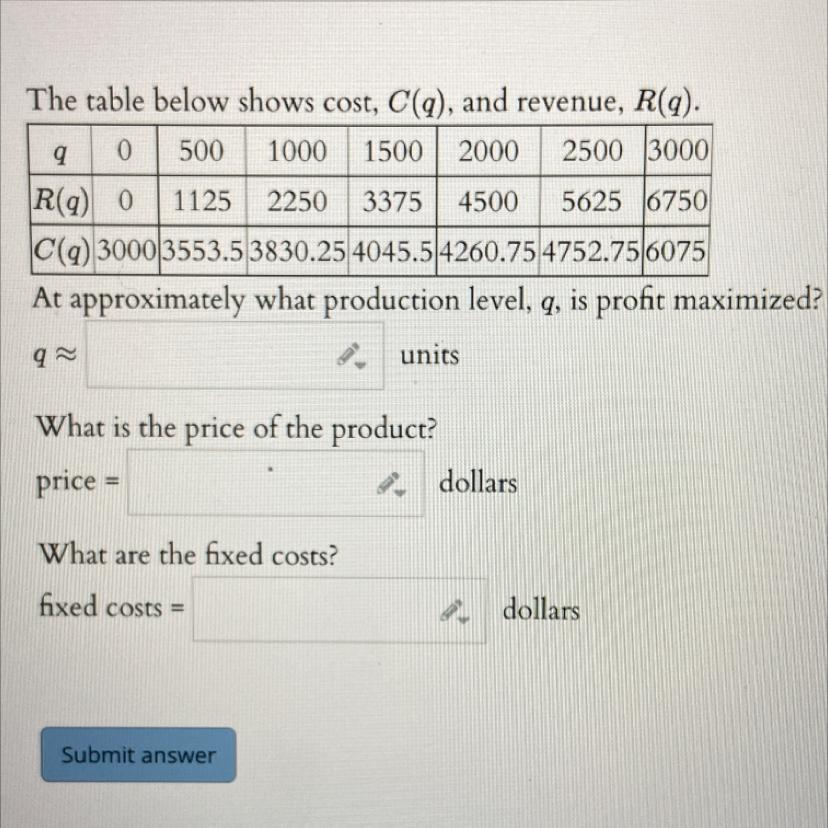
Answers
From the given table ,
\(\begin{gathered} \text{Profit = }Revenue\text{ - Cost} \\ \end{gathered}\)Profit is maximum at
\(5625-4752.75\text{ = 872.25}\)Therefore ,
\(q\text{ = 2500 units }\)Price of the product is
\(P\text{ = }\frac{R(q)}{q}=\text{ }\frac{5625}{2500}\text{ = 2.25}\)Therefore
\(\text{Price = 2.25 dollars}\)Thus the fixed cost is
\(C(0)\text{ = }3000\text{ dollars}\)help Please ill give branliest.
The juniors and seniors at a high school are ordering class shirts. The amounts ordered in each size are shown in the two-way frequency table below.
Small Medium Large X-Large Total
Juniors 65 84 68 23 240
Seniors 51 62 79 28 220
Total 116 146 147 51 460
Which statement is true about the information represented in the table?
A The percentage of Seniors who ordered a large shirt is greater than the percentage of students who ordered a large shirt who are also in the Senior class.
B The percentage of Seniors who ordered a small shirt is the same as the percentage of students who ordered a small shirt who are also in the Senior class.
C The percentage of Juniors who ordered a medium shirt is greater than the percentage of students who ordered a medium shirt who are also in the Junior class.
D The percentage of Juniors who ordered a medium shirt is less than the percentage of students who ordered a medium shirt who are also in the Junior class.
Answers
Answer:
it b
Step-by-step explanation:
To determine which statement is true, we need to calculate the percentages for each option and compare them and option c is correct.
Option A: The percentage of Seniors who ordered a large shirt is greater than the percentage of students who ordered a large shirt and are also in the Senior class. To calculate the percentage of Seniors who ordered a large shirt, we divide the number of Seniors who ordered a large shirt by the total number of Seniors:
Percentage of Seniors who ordered a large shirt =\((79 / 220) * 100 = 35.91\)% To calculate the percentage of students who ordered a large shirt and are also in the Senior class, we divide the number of Seniors who ordered a large shirt by the total number of students who ordered a large shirt: Percentage of students who ordered a large shirt and are also in the Senior class \(= (79 / 147) * 100 = 53.74\)% Since the percentage of students who ordered a large shirt and are also in the Senior class is greater than the percentage of Seniors who ordered a large shirt, statement A is false.
Similarly, we can calculate the percentages for the other options: Option B: The percentage of Seniors who ordered a small shirt is the same as the percentage of students who ordered a small shirt and are also in the Senior class. Percentage of Seniors who ordered a small shirt \(= (51 / 220) * 100 = 23.18\)% Percentage of students who ordered a small shirt and are also in the Senior class \(= (51 / 116) * 100 = 43.97\) % Since the percentages are not the same, statement B is false.
Option C: The percentage of Juniors who ordered a medium shirt is greater than the percentage of students who ordered a medium shirt and are also in the Junior class. Percentage of Juniors who ordered a medium shirt \(= (84 / 240) * 100 = 35\)% Percentage of students who ordered a medium shirt and are also in the Junior class \(= (84 / 146) * 100 = 57.53\)% Since the percentage of students who ordered a medium shirt and are also in the Junior class is greater than the percentage of Juniors who ordered a medium shirt, statement C is true.
Hence the correct option is C.
To know more about percentages visit:
https://brainly.com/question/32197511
#SPJ2
Solve for x:
42=3x+6
Question 2 options:
x=-16
x=16
x=12
x=14
Answers
Answer:
42=3x+6
subtract 6 from both sides
42-6=3x+6-6
to get
36=3x
divide both sides by 3 to isolate x
36/3=3x/3
to get
12=x
A rectangular pyramid has a base that is three times as long as it is wide. The volume of the pyramid is 75 ft³ and the height is 3 feet. What is the perimeter of the base?
Answers
The perimeter of the base of the rectangular pyramid is 40 ft.
To find the perimeter of the base of the rectangular pyramid, we first need to determine the dimensions of the base. Let's denote the width of the base as "w" and the length as "l".
Given that the base is three times as long as it is wide, we have:
l = 3w
To find the volume of the pyramid, we can use the formula:
Volume = (1/3) * Base Area * Height
Since the height is given as 3 feet and the volume is 75 ft³, we can rewrite the formula as:
75 = (1/3) * Base Area * 3
Simplifying the equation, we have:
Base Area = 75 / 1 = 75 ft²
The base area of a rectangle is given by the formula:
Base Area = Length * Width
Substituting the value of the length from the earlier equation (l = 3w), we have:
75 = 3w * w
75 = 3w²
Dividing both sides by 3, we get:
25 = w²
Taking the square root of both sides, we find:
w = √25
w = 5 ft
Substituting the value of w into the equation for l = 3w, we have:
l = 3 * 5 = 15 ft
Therefore, the width of the base is 5 ft and the length is 15 ft.
Now, we can calculate the perimeter of the base by adding up all the sides:
Perimeter = 2 * (Width + Length)
Perimeter = 2 * (5 + 15)
Perimeter = 2 * 20
Perimeter = 40 ft
Hence, the perimeter of the base of the rectangular pyramid is 40 ft.
Learn more about rectangular pyramid at https://brainly.com/question/32034890
#SPJ11
Someone can help me pls

Answers
1 1/2 ÷ 12=
please answer my question
Answers
Answer:
0.125
Step-by-step explanation:
Answer:
.125 bc I use a calendar
Step-by-step explanation:
that assignment
two families with four people in each family go to a movie theater. in how many ways can they be seated
Answers
According to probability, if both families want to sit together, they can be seated in a row a maximum of two times.
What seating configuration?The direction that each person is facing is crucial when arranging the people.
In order to determine how many ways they can be seated in a row if both families want to sit together, imagine that two families with four members each attend a movie theatre.
Given that the arrangement is important, we will apply the permutation rule. We'll divide the remaining four into two groups of four each.
There are two different ways to arrange the groups so they can sit together.
2! = 2 * 1
2! = 2ways
To know more about probability visit:-
brainly.com/question/11234923
#SPJ4
\( \sqrt{3x + 4} - \sqrt{x + 5} = 1\)
Answers
x=4
Good luck !!!
Answer:
x=4
Step-by-step explanation:
See some of the steps below:) you can use the app photo math. you just take a picture of the problem and it gives you the answer and explains the steps:)
![[tex] \sqrt{3x + 4} - \sqrt{x + 5} = 1[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/O45AmA3BTkqhrgkF0f3d2D304ZW85ALW.jpeg)