The graph represents a quadratic function. Write an equation of the function in standard form.

Answers
The equation for the quadratic function in standard form is 4x² - 16x - 9
Writing Quadratic equationFrom the question, we are to write an equation for the quadratic function in standard form.
From the given quadratic graph,
The roots of the function are -0.5 and 4.5.
That is,
x = -0.5 and x = 4.5
That is,
x = -1/2 and x = 9/2
Therefore,
2x = -1 and 2x = 9
The factors of the quadratic function are (2x + 1) and (2x - 9)
Thus,
We can write that
(2x + 1)(2x - 9) = 0
4x² - 18x + 2x - 9 = 0
Simplify
4x² - 16x - 9 = 0
Hence, the equation is f(x) = 4x² - 16x - 9
Learn more on Writing quadratic equation here: brainly.com/question/23991455
#SPJ1
Related Questions
What is 3(x-1)+4=12 ?
Answers
Answer:
3.66666. . . = 11/3 = 3 2/3
Step-by-step explanation:
Use distributive property.
3 ⋅ x = 3x
3 ⋅ (-1) = -3
3x - 3 + 4 = 12
Add -3 to 4
1
3x + 1 = 12
Subtract 1 from both sides.
3x = 11
Divide both sides by 3
3.666666. . .
This can also be written as 11/3
11/3 can be simplified to 3 2/3
Hope I helped :)
Please consider Brainliest :)
find the exact length of the curve. x = 5 12t2, y = 3 8t3, 0 ≤ t ≤ 3
Answers
To find the exact length of the curve defined by the parametric equations x = 5t^2 and y = 3t^3, where 0 ≤ t ≤ 3, we can use the arc length formula for parametric curves.
The arc length formula for a parametric curve defined by x = f(t) and y = g(t) over the interval [a, b] is given by:
L = ∫[a,b] √[ (dx/dt)^2 + (dy/dt)^2 ] dt
In this case, we have x = 5t^2 and y = 3t^3, with the parameter t ranging from 0 to 3.
First, we need to find the derivatives of x and y with respect to t:
dx/dt = d/dt (5t^2) = 10t
dy/dt = d/dt (3t^3) = 9t^2
Next, we substitute these derivatives into the arc length formula:
L = ∫[0,3] √[ (10t)^2 + (9t^2)^2 ] dt
L = ∫[0,3] √(100t^2 + 81t^4) dt
Now, we can integrate the expression inside the square root with respect to t:
L = ∫[0,3] √(100t^2 + 81t^4) dt
L = ∫[0,3] t√(100 + 81t^2) dt
Unfortunately, this integral does not have a simple closed-form solution. We would need to evaluate it numerically using numerical integration techniques or computer software.
So, the exact length of the curve cannot be determined algebraically. However, it can be approximated using numerical methods.
Learn more about length here: brainly.com/question/32388292
#SPJ11
Let t represent the number of months since January. The number of termites in a nest in any given month can be represented by the function < f(t)=4(3)t The number of ants in a box can be represented by the function in the table:
Month 0 1 2 3 4
Number 20 45 101 228 513
What is the positive difference between the original number of termites in the nest and the original number of ants in the box?
Answers
The positive difference between the original number of termites in the nest and the original number of ants in the box is 16
Calculating the positive difference between original number of termites and original number of antFrom the question, we are to determine the positive difference between the original number of termites in the nest and the original number of ants in the box
From the given information,
The number of termites is represented by the function
f(t) = 4(3)^t
The original number of termites is the number of termites present at 0 months
To determine the original number of termites, we will set t = 0
f(t) = 4(3)^t
f(0) = 4(3)^0
f(0) = 4(1)
f(0) = 4
Therefore original number of termites is 4
Now, we will determine the original number of ants in the box
From the given table,
The original number of ants is 20
Thus,
The positive difference = 20 - 4
The positive difference = 16
Hence, the positive difference is 16
Learn more on Calculating positive difference here: https://brainly.com/question/28868405
#SPJ1
Answer: it is 16. i got it right on the test!

Una compañía de renta de carros. Si renta un auto chico su cuenta se divide en dos partes: $300 por día, $2 por kilometro recorrido, supón que rentas el auto por un día. 1.- si rentas el auto por un día y recorres 50 kilómetros, ¿Cuál es el precio de renta? 2.- determina una función que relacione el precio de renta con los kilómetros recorridos 3.- Si rentas el auto por un día ¿Cuántos kilómetros podrás recorrer si deseas que el precio de renta sea de $500? 4.- La función determinada en el puntos es: A) Constante B) Lineal C) Racional D)Trascendente
Answers
Si alquilas el auto por un día y recorres 50 kilómetros, el precio del alquiler es de $400
Si rentas un auto por un día y recorres 50 kilómetros, el precio de renta será
$300 por día + $2 por kilómetro recorrido * 50 kilómetros
= $300 + $100 = $400.
La función que relaciona el precio de renta con los kilómetros recorridos se puede expresar como
P = 300 + 2K,
donde P es el precio de renta en dólares y K es la cantidad de kilómetros recorridos.
Si rentas un auto por un día y deseas que el precio de renta sea de $500, podemos utilizar la función determinada en el punto 2 para calcular la cantidad de kilómetros que puedes recorrer.
Reemplazando P = 500 en la función, tenemos
500 = 300 + 2K, entonces 200 = 2K, entonces K = 100.
Por lo tanto, puedes recorrer 100 kilómetros si deseas que el precio de renta sea de $500.
La función determinada en el punto 2 es lineal, ya que relaciona una variable dependiente (el precio de renta) con una variable independiente (los kilómetros recorridos) de manera lineal. Por lo tanto, la respuesta es is Lineal.
To learn more about precio :
https://brainly.com/question/19129430
#SPJ4
Solve the above que no. 55

Answers
Answer:
Let \(\left(1+\frac{1}{\tan^{2}A} \right)\cdot \left(1+\frac{1}{\cot^{2}A} \right)\), we proceed to prove the trigonometric expression by trigonometric identity:
1) \(\left(1+\frac{1}{\tan^{2}A} \right)\cdot \left(1+\frac{1}{\cot^{2}A} \right)\) Given
2) \(\left(1+\frac{\cos^{2}A}{\sin^{2}A} \right)\cdot \left(1+\frac{\sin^{2}A}{\cos^{2}A} \right)\) \(\tan A = \frac{1}{\cot A} = \frac{\sin A}{\cos A}\)
3) \(\left(\frac{\sin^{2}A+\cos^{2}A}{\sin^{2}A} \right)\cdot \left(\frac{\cos^{2}A+\sin^{2}A}{\cos^{2}A} \right)\)
4) \(\left(\frac{1}{\sin^{2}A} \right)\cdot \left(\frac{1}{\cos^{2}A} \right)\) \(\sin^{2}A+\cos^{2}A = 1\)
5) \(\frac{1}{\sin^{2}A\cdot \cos^{2}A}\)
6) \(\frac{1}{\sin^{2}A\cdot (1-\sin^{2}A)}\) \(\sin^{2}A+\cos^{2}A = 1\)
7) \(\frac{1}{\sin^{2}A-\sin^{4}A}\) Result
Step-by-step explanation:
Let \(\left(1+\frac{1}{\tan^{2}A} \right)\cdot \left(1+\frac{1}{\cot^{2}A} \right)\), we proceed to prove the trigonometric expression by trigonometric identity:
1) \(\left(1+\frac{1}{\tan^{2}A} \right)\cdot \left(1+\frac{1}{\cot^{2}A} \right)\) Given
2) \(\left(1+\frac{\cos^{2}A}{\sin^{2}A} \right)\cdot \left(1+\frac{\sin^{2}A}{\cos^{2}A} \right)\) \(\tan A = \frac{1}{\cot A} = \frac{\sin A}{\cos A}\)
3) \(\left(\frac{\sin^{2}A+\cos^{2}A}{\sin^{2}A} \right)\cdot \left(\frac{\cos^{2}A+\sin^{2}A}{\cos^{2}A} \right)\)
4) \(\left(\frac{1}{\sin^{2}A} \right)\cdot \left(\frac{1}{\cos^{2}A} \right)\) \(\sin^{2}A+\cos^{2}A = 1\)
5) \(\frac{1}{\sin^{2}A\cdot \cos^{2}A}\)
6) \(\frac{1}{\sin^{2}A\cdot (1-\sin^{2}A)}\) \(\sin^{2}A+\cos^{2}A = 1\)
7) \(\frac{1}{\sin^{2}A-\sin^{4}A}\) Result
L2.10.2 Quir. Bisectors and Midsegments
The Dragram snOWS ARC When termes des point
M
O A. Circumcenter
O B. Incenter
O c. Centrold
O d. Orthocenter
Answers
susan is making a blanket. she bought 1/3 pf a yard of material to use for the border for the blanket.susant cut the material into 4 same-size strips. what part of a whole yard is each strip
Answers
The fraction of the material that each strip represents is 1/12 of a yard.
Susan bought 1/3 of a yard of material to use for the border for the blanket. She cut the material into 4 same-size strips. The problem is asking for the part of a whole yard that each strip represents.
Since Susan has 1/3 of a yard of material and she cut it into 4 same-size strips, we can use division to find the fraction of the material that each strip represents.
Therefore, the fraction of the material that each strip represents is 1/3 ÷ 4.
To divide fractions, we multiply the first fraction by the reciprocal of the second fraction.
The reciprocal of 4 is 1/4, so we can rewrite the expression as:
1/3 ÷ 4 = 1/3 × 1/4
Now we can multiply the fractions:
1/3 × 1/4 = 1/12
Therefore, each strip represents 1/12 of the whole yard of material.
To know more about the "fraction": https://brainly.com/question/27903912
#SPJ11
Distributive Property to solve the equation. 5(x - 6) + 8 = 7x- 8 (Type the value of x.)
Answers
Answer:
x=−7
Solving for X:
Step 1: Simplify both sides of your equation.
5x−22=7x−8
Step 2: Subtract 7x from both sides.
5x−22−7x=7x−8−7x
−2x−22=−8
Step 3: Add 22 to both sides.
−2x−22+22=−8+22
−2x=14
Step 4: Divide both sides by -2.
-2x/-2 = 14/-2
^ x = -7
THEREFORE:
x is −7
ANSWER SOON PLSSSSI'm so sorry for asking lots of questions! Tyler wants to go to the County Fair on Wednesday with his friends. On Wednesday, you can buy a wristband that allows an unlimited number of rides all night.
If the cost is $7.50 for 1 wrist band, how many would 3 wrist bands cost?
Answers
Answer:
22.50 per 3 wristbands is the cost
A 6-sided die is tossed. Find P (even | less than 3).
Answers
The value of probability P (even | less than 3) is, 1/3.
What is mean by Probability?The term probability refers to the likelihood of an event occurring. Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one.
Given that;
A 6-sided die is tossed.
Here, Two numbers 1 and 2 are less than 3.
Hence, The value of P (even | less than 3) is,
⇒ 2 / 6
⇒ 1 / 3
Thus, The value of P (even | less than 3) is, 1/3.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
If p=180−0.2D, calculate the optimal profit if the total cost is $30,500.
Answers
To calculate the optimal profit, we need to find the value of D when the total cost is \($30,500\) and then substitute it into the given equation.
To find D, we can rearrange the equation to solve for D: Given:\(p = 180 - 0.2D\) and total cost =\($30,500\) Now, substitute the total cost ($30,500) into the equation to find D:
Since D cannot be negative in this context, it means that the given equation is not applicable for a total cost of \($30,500\). it is not possible to calculate the optimal profit using the given equation and the total cost of \($30,500\).
To know more about cost visit:
https://brainly.com/question/14566816
#SPJ11
A nurse is providing discharge education to the parents of preschooler who is prescribed acetaminophen (Tylenol) 300 mg every 4 hr as needed. The acetaminophen liquid suspension that has been prescribed provides 120 mg/S mL. How many teaspoons should the nurse teach the parents to administer per does?
Answers
The nurse should teach the parents to administer 2.5 teaspoons of the acetaminophen liquid suspension per dose.
The prescribed dosage of acetaminophen is 300 mg every 4 hours as needed. The liquid suspension provides 120 mg of acetaminophen per 5 mL (1 teaspoon). To determine the number of teaspoons required for the prescribed dosage, we can set up a proportion:
120 mg / 5 mL = 300 mg / x mL
Cross-multiplying, we get:
120 mg * x mL = 5 mL * 300 mg
Simplifying, we have
120x = 1500
Dividing both sides by 120, we find:
x = 1500 / 120 = 12.5 mL
Since there are 5 mL (1 teaspoon) in each dose, we can convert 12.5 mL to teaspoons:
12.5 mL / 5 mL = 2.5 teaspoons
Therefore, the nurse should teach the parents to administer 2.5 teaspoons of the acetaminophen liquid suspension per dose to ensure the child receives the prescribed dosage of 300 mg.
Learn more about proportion here:
https://brainly.com/question/31010676
#SPJ11
A baby was born with a weight of 10 pounds and then began to gain 2 pounds per month. Write an equation for W, in terms of t, representing weight, in pounds, of the newborn baby t months after birth
Answers
Answer: 10+2t
Step-by-step explanation: I guess not sure sorry
An isosceles triangle has an angle that measures 118°. Which other angles could be in that isosceles triangle? Choose all that apply. a 69° b 31 c 118 d 54
Answers
Answer:
b. 31.
Step-by-step explanation:
The other 2 angles in the triangle are congruent so they are:
(180 - 118) / 2
= 31 degrees.
The possible measure of two similar angles in an isosceles triangle could be b. 31 °
What is a triangle?A triangle is a three-sided closed-plane figure formed by joining three noncolinear points. Based on the side property triangles are of three types they are Equilateral triangle, Scalene triangle, and Isosceles triangle.
We know in an isosceles triangle two sides are equal and angles opposite sides to the equal side are also equal.
We also know that the sum of all the interior angles in a triangle is 180°.
Let, The similar angles be 'x'.
Therefore,
x + x + 118 = 180
2x = 62.
x = 31°.
learn more about the isosceles triangle here :
https://brainly.com/question/2456591
#SPJ2
drop downs are for the first one


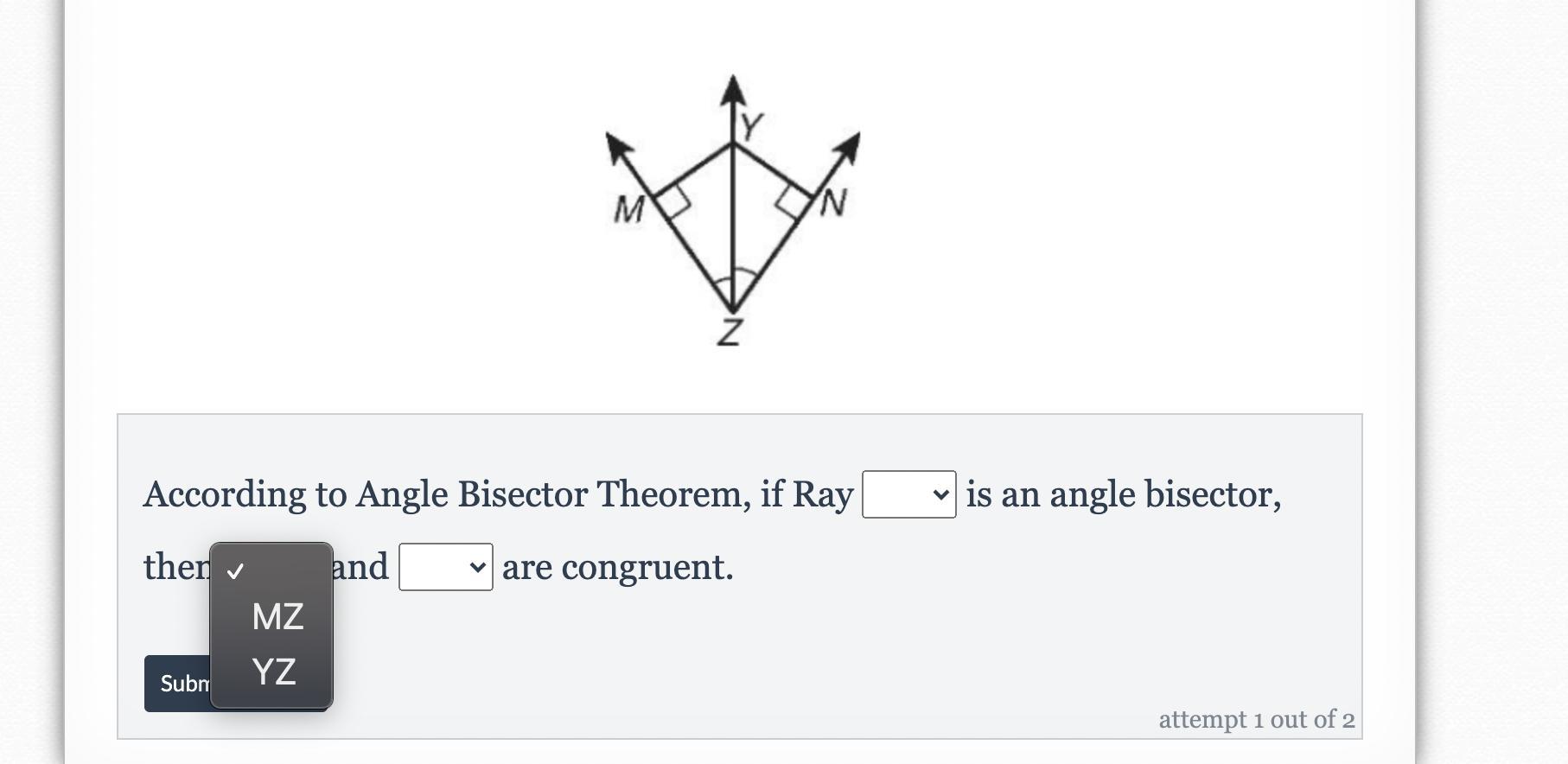


Answers
Answer:
According to Angle Bisector Theorem, if Ray YZ is an angle bisector, then MZ and NZ are congruent.
EH= 23. It is shown that ray FH bisects EFG, EF and EH are perpendicular, FG and HG are perpendicular. Then EH and GH are congruent. Therefore since GH= 23, then EH= 23
Find the percent of change when 23 is increased to 34. If necessary, round your answer to the nearest tenth.
A. 32.4% decrease
B. 47.8% increase
C. 32.4% increase
D.47.8% decrease
Answers
Answer:
B. 47.8% increase
Step-by-step explanation:
34-23= 11
11/23= 0.478 or 47.8%
In Exercises 43 through 46, solve the given separable initial value problem. 43. dx/dy =−2y;y=3 when x=0 44. dx/dy =xy;y=1 when x=0 45. dx/dy = e^x+y
;y=0 when x=0 46. dx/dy = √(y/x);y=1 when x=1
Answers
The solution to the initial value problem is √x = (1/3) \(y^{\frac{3}{2} }\) + 2/3.
Given: dx/dy = -2y, y = 3 when x = 0
To solve this, we'll separate the variables and integrate:
dx = -2y dy
Integrating both sides:
∫ dx = ∫ -2y dy
x = - \(y^{2}\) + C
Now we can apply the initial condition y = 3 when x = 0:
0 = - \(3^{2}\) + C
C = -9
Therefore, the solution to the initial value problem is x = - \(y^{2}\) - 9.
Given: dx/dy = xy, y = 1 when x = 0
We'll again separate the variables and integrate:
dx = xy dy
Integrating both sides:
∫ dx = ∫ xy dy
x = (1/2)\(y^{2}\) + C
Applying the initial condition y = 1 when x = 0:
0 = (1/2) \(1^{2}\) + C
C = -1/2
Thus, the solution to the initial value problem is x = (1/2)\(y^{2}\) - 1/2.
Given: dx/dy = \(e^{x+y}\), y = 0 when x = 0
Separating the variables and integrating:
dx = \(e^{x+y}\) dy
∫ dx = ∫ \(e^{x+y}\) dy
x = \(e^{x+y}\) + C
Using the initial condition y = 0 when x = 0:
0 = \(e^{0+0}\) + C
C = -1
Hence, the solution to the initial value problem is x = \(e^{x+y}\) - 1.
Given: dx/dy = √(y/x), y = 1 when x = 1
Again, separating the variables and integrating:
dx/√x = √y dy
Integrating both sides:
2√x = (2/3)\(y^{\frac{3}{2} }\) + C
Simplifying:
√x = (1/3)\(y^{\frac{3}{2} }\) + C
Applying the initial condition y = 1 when x = 1:
1 = (1/3)\(1^{\frac{3}{2} }\) + C
C = 2/3
Therefore, the solution to the initial value problem is √x = (1/3) \(y^{\frac{3}{2} }\) + 2/3.
To learn more about exponent, refer:-
brainly.com/question/30066987
#SPJ4
Which expression is equivalent to
(6x-9x) - (2x - 3)?

Answers
Answer:
6x^2 -9x -2x-3
6x^2 -11x +3
Step-by-step explanation:
Answer: -5x+3 hope this helps
Step-by-step explanation:
x + y = -2 .
- 3x + y=6
solve the system of linear equations by substitution
Answers
What is the most prescise classification of this shape?

Answers
Answer:
the answer for this question isnparallelogram
Answer:
Parallelogram
Step-by-step explanation:
How large should we choose n so that the trapezoid-rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001? (Use the error bound given in Section 5.9 of the course text.)
Answers
The trapezoidal rule is a numerical integration method that uses trapezoids to estimate the area under a curve. The trapezoidal rule can be used for both definite and indefinite integrals. The trapezoidal rule approximation, Tn, to the integral sin r dz is given by:
Tn = (b-a)/2n[f(a) + 2f(a+h) + 2f(a+2h) + ... + 2f(b-h) + f(b)]where h = (b-a)/n. To determine how large n should be so that Tn is accurate to within 0.00001, we can use the error bound given in Section 5.9 of the course text. According to the error bound, the error, E, in the trapezoidal rule approximation is given by:E ≤ ((b-a)³/12n²)max|f''(x)|where f''(x) is the second derivative of f(x). For the integral sin r dz, the second derivative is f''(r) = -sin r. Since the absolute value of sin r is less than or equal to 1, we have:max|f''(r)| = 1.
Substituting this value into the error bound equation gives:E ≤ ((b-a)³/12n²)So we want to choose n so that E ≤ 0.00001. Substituting E and the given values into the inequality gives:((b-a)³/12n²) ≤ 0.00001Simplifying this expression gives:n² ≥ ((b-a)³/(0.00001)(12))n² ≥ (b-a)³/0.00012n ≥ √(b-a)³/0.00012Now we just need to substitute the values of a and b into this expression. Since we don't know the upper limit of integration, we can use the fact that sin r is bounded by -1 and 1 to get an upper bound for the integral.
For example, we could use the interval [0, pi/2], which contains one full period of sin r. Then we have:a = 0b = pi/2Plugging in these values gives:n ≥ √(pi/2)³/0.00012n ≥ 5073.31Since n must be an integer, we round up to the nearest integer to get:n = 5074Therefore, we should choose n to be 5074 so that the trapezoidal rule approximation, Tn, to the integral sin r dz is accurate to within 0.00001.
To know more about integration visit :
https://brainly.com/question/31744185
#SPJ11
Manuel runs 4.06 kilometers every morning. One day, he runs 1.94 kilometers and then stops
to take a break. How much further does Manuel have left to run?
Answers
Answer:
2.12 kilometers
Step-by-step explanation:
Manuel needs to run a total of 4.06 kilometers. He only has 1.94, so to find the amount he still needs, we can make an equation of 4.06-1.94 = x. Solve that and we get x = 2.12, so Manuel still needs to run 2.12 kilometers to run 4.06 kilometers.
Which linear equation is represented by the table?
X-2 136
Y 7 4 2-1
A. y = -x + 5
B. y = 2x - 1
c. y = x + 3
D. y = -3x + 11
Answers
Answer:
A
Step-by-step explanation:
Find the rise over run (gradient) between two points. Choosing x=-2 and x=1 we get (1 - - 2) / (4 - 7) = -3/3 = -1. This means that m in y=mx+c is -1 so it is either A or C. If we then try a pair of x and y with y = -x + c we can get c. Using the first pair: 7=-1*-2+c = 2 + c so c = 5, leaving us with y = -x + 5.
Alternatively try all 4 with the numbers, if plugging in that value of x gives you that value of y then it is the correct equation.
Answer:
a
Step-by-step explanation:
Which of the following expressions are undefined?
Choose all answers that apply:
A
C
3
-0
033 10

Answers
The expressions (a) 3 / -0 and (c) 3 / 0 are undefined.
To determine which of the following expressions are undefined, let's analyze each expression:
a. 3 / -0:
Division by zero is undefined in mathematics. Therefore, the expression 3 / -0 is undefined.
b. 0 / 3:
This expression represents the division of zero by a non-zero number. In mathematics, dividing zero by a non-zero number is defined and yields the value of zero. Thus, the expression 0 / 3 is defined.
c. 3 / 0:
Similar to expression (a), division by zero is undefined in mathematics. Therefore, the expression 3 / 0 is also undefined.
In conclusion, the expressions that are undefined are (a) 3 / -0 and (c) 3 / 0.
for such more question on expression
https://brainly.com/question/4344214
#SPJ8
On 1 st March, 2020 Mr. Mohit started a Furniture business in GANDHI NAGAR Mr. Mohit invested Rs 50,00,000.
Answers
Answer:
Answer to the following question is as follows;
Step-by-step explanation:
Given:
Amount invested by Mr. Mohit = Rs. 50,00,000
Computation:
Books of (...... LTD)
Journal entries
Date Particular Debit Credit
March 1 Cash A/C Dr. 50,00,000
To Capital A/C Cr. 50,00,000
(Being Amount invested in new business)
For what values of m does the graph of y = 3x^2+ 7x + m have two x-intercepts?
Answers
Answer:
m < 49/12
Step-by-step explanation:
The portion of the quadratic formula under the square root sign is the discriminant.
If the discriminant is > 0 then there are two real roots.
b² -4ac > 0
-----------------------------
7² - 4(3)m > 0
49 - 12m > 0
Subtract 49 from both sides
-12m > -49
Divide both sides by -12
(when multiplying or dividing by a negative the inequality must be reversed)
m < 49/12
Prove the triangles are similar.

Answers
Answer:
SAS similarity
Step-by-step explanation:
The two triangles MON and MQP are such that
Angle M = Angle M
MO/MQ = MN/MP
Therefore, Triangle MON ~ Triangle MQP (SAS similarity)
Answer the following questions below: True or False
- A survey timeline indicates the date for activation of the measurement instrument.
True or False
- Instrument disposition can involve the creation and delivery to a dropbox for paper-and-pencil instruments.
True or False
- Participant data entry can increase the accuracy of a data record.
True or False
- A significant number of "Don’t Know" responses to a closed measurement question may mean that the measurement instrument failed to provide appropriate response categories.
True or False
- When cross-tabulation is used in CFA for testing purposes, it’s called a contingency table.
True or False
- Percentages translate the data to a base of 100, paving the way for relative comparisons between variables.
True or False
Answers
The answer to the questions on instrument are:
True
True
True
True
False
True
How to answer the questions below: True or False?True: A survey timeline typically includes various dates related to the survey administration, such as the start and end dates for participant recruitment, the date for activation of the measurement instrument, and the deadline for completing the survey. The date for activation of the measurement instrument refers to the date on which the survey respondents can begin answering the questions.
True: Instrument disposition refers to the process of distributing and collecting the measurement instruments. This can involve various methods, such as mailing the instruments to the participants or delivering them to a dropbox for paper-and-pencil instruments.
True: Participant data entry can increase the accuracy of a data record because it eliminates the need for manual data entry, which can introduce errors. With participant data entry, the participants themselves enter their responses directly into a computer or mobile device, ensuring that the data is accurate and complete.
True: A significant number of "Don’t Know" responses to a closed measurement question may indicate that the measurement instrument failed to provide appropriate response categories. If the survey respondents are unsure about how to answer a question and there is no appropriate response option available, they may select "Don’t Know" instead.
False: Cross-tabulation in CFA (Confirmatory Factor Analysis) is typically used to examine the relationship between two or more variables, and it is not called a contingency table. A contingency table is a table used to display the frequencies and/or percentages of two or more categorical variables.
True: Percentages are a way of expressing data in relation to a base of 100, making it easier to compare variables. For example, if 80 out of 100 respondents answered "Yes" to a question, we can say that the percentage of respondents who answered "Yes" is 80%. This allows us to compare the percentage of "Yes" responses to other questions or variables in the survey.
Learn more about measurement instrument on:
https://brainly.com/question/787793
#SPJ1
Determine the value of y, if x is 4.
y= | x - 7 |

Answers
Answer: y = 3
Step-by-step explanation:
A student plays a total of 20
rounds of Rock Paper
Scissors. He wins 75% of
them. How many rounds did
he win?
Answers
Answer: The student wins 15 rounds.
Step-by-step explanation:
The number of rounds the student won is required.
The number of rounds the student won was 15.
The total number of rounds played is \(20\).
The percentage the student wins is \(75\%\)
The number of times he won was
\(20\times 75\%\\ =20\times \dfrac{75}{100}\\ =20\times 0.75\\ =15\)
The number of rounds the student won was 15.
Learn more:
https://brainly.com/question/23318129
https://brainly.com/question/14532195