The graph of the parent function f(x) = xº is translated to form the graph of g(x) = (x - 4) 3 - 7. The point (0, 0) on the
graph of f) corresponds to which point on the graph of g(x)?
Answers
Answer: The point (0, 0) corresponds to the point (4, -7)
Step-by-step explanation:
We have the function f(x) = x^3
And we transform this to get:
g(x) = (x - 4)^3 - 7
Here we have a vertical translation and a horizontal shift, let's define these two shifts:
Vertical shift.
If we have a function f(x), a vertical shift of N units is written as:
g(x) = f(x) + N
This will move the graph of f(x) up or down a distance of N units.
if N is positive, then the shift is upwards
if N is negative, then the shift is downwards.
Horizontal shift.
If we have a function f(x), a horizontal shift of N units is written as:
g(x) = f(x + N)
This will move the graph of f(x) to the right or left a distance of N units.
if N is positive, then the shift is to the left
if N is negative, then the shift is to the right.
Then if we start with f(x), g(x) is a translation of 7 units down and 4 units to the right.
This means that any point (x, y) that belongs to the graph of f(x), after the transformation will be (x + 4, y - 7)
Then the point (0, 0) of the original function corresponds to the point (0 + 4, 0 - 7) = (4, - 7) of the function g(x)
We can check this, we need to evaluate the function g(x) in x = 4
g(4) = (4 - 4)^3 - 7= 0 - 7 = -7
g(4) = -7
Then the point (4, -7) belongs to the graph of g(x).
Related Questions
Given the kite below, if NO = 5 and OM = 12, what is the value of NM?

Answers
Answer:
NM = 13
Step-by-step explanation:
pythagorean theorem: \(a^{2} + b^{2} = c^{2}\)
a or NO = 5
b or OM = 12
c or NM = ?
plug in what is known:
⇒ \(5^{2} + 12^{2} = c^{2}\)
⇒ \(25 + 144 = c^{2}\)
⇒ 169 = \(c^{2}\)
square root each side of the equation:
⇒ \(\sqrt{169} = \sqrt{c^{2} }\)
solve:
⇒ 13 = c
devide 240g in to the ratio 5:3:4
Answers
• 5/12 * 240 = 100
• 3/12 * 240 = 60
• 4/12 * 240 = 80
Find all solutions in the interval [0,2π). Give exact answers.
tan 2x = √3
Answers
Answer:
The exact solutions in the interval [0,2π) are x = π/6, 5π/6, 7π/6 and 11π/6
Step-by-step explanation:
yw;)
Work through the following steps to find the area under f(x)=x^2+3 on [0,9], using the limit definition.
a) We know that a=_____ and b=_____
b) Using n subintervals, Δx= ______
c) Assume that the sample points in each interval are right endpoints. Find the following sample points:
x_1= _____
x_2= _____
x_3= _______
In general, the i th sample point is xi= _____
Note: your answer will be an expression in terms of i and n.
Answers
The value of i th sample point is xi = 9i/n.
a) The given function is f(x) = x² + 3 and we need to find the area under the curve of the function on [0, 9]. Here a is the lower limit of the interval and b is the upper limit of the interval.
So, we have a = 0 and b = 9.
b) We are required to use n subintervals to evaluate the area.Δx is the width of each subinterval.
So, we have
Δx = (b - a) / n
= (9 - 0) / n
= 9/n
c) The sample points for the right endpoints for each interval can be determined as follows:
x1 = a + Δx
= 0 + 9/n
= 9/nx2
= a + 2
Δx = 0 + 2(9/n)
= 18/n
x3 = a + 3
Δx = 0 + 3(9/n) = 27/n
and in general
xi = a + i
Δx = 0 + i(9/n) = 9i/n
Therefore, the value of i th sample point is xi = 9i/n.
Note: As we need to find the area using limit definition, the expression would be a summation of f(xi)Δx where i goes from 1 to n, i.e., ∑f(xi)Δx from i = 1 to n.
To learn more about function visit;
https://brainly.com/question/30721594
#SPJ11
the scores on a mathematics exam have a mean of 70 and a standard deviation of 5. find the x-value that corresponds to the z-score 2.33.
Answers
x-value that corresponds to the z-score of 2.33 is 81.65.
Mean = 70
Standard deviation = 5
z score = 2.33
Using the z-score formula:
z = (x - mean) / SD
Plug the values:
2.33 = (x-70)/5
x = 5(2.33) +70
x = 81.5
Find out more information about the z-score here: brainly.com/question/17436641
#SPJ4
What is the mathematical expression for modified Reynolds Analogy, also known as Chilton-Colburn analogy?
Answers
The modified Reynolds analogy, also known as the Chilton-Colburn analogy, is expressed mathematically as Nu = f * Re^m * Pr^n. It relates the convective heat transfer coefficient (h) to the skin friction coefficient (Cf) in fluid flow. This equation is widely used in heat transfer analysis and design applications involving forced convection.
The modified Reynolds analogy is a useful tool in heat transfer analysis, especially for situations involving forced convection. It provides a correlation between the heat transfer and fluid flow characteristics. The Nusselt number (Nu) represents the ratio of convective heat transfer to conductive heat transfer, while the Reynolds number (Re) characterizes the flow regime. The Prandtl number (Pr) relates the momentum diffusivity to the thermal diffusivity of the fluid.
The equation incorporates the friction factor (f) to account for the energy dissipation due to fluid flow. The values of the constants m and n depend on the flow conditions and geometry, and they are determined experimentally or by empirical correlations. The modified Reynolds analogy is widely used in engineering calculations and design of heat exchangers, cooling systems, and other applications involving heat transfer in fluid flow.
Learn more about Prandtl number here:
https://brainly.com/question/32353670
#SPJ11
What is the answer to 24 divided by -3.2??
Please provide instructions if you can.

Answers
Answer:-7.5
Step-by-step explanation:
If we take out the negative and make it 24 ÷ 3.2, it would be 7.5 since 3.2 would go into 24 7.5 times. But since we changed it to figure it out, we have to change it back with the rule that "a negative x negative is a positive" meaning that the
24 ÷ 3.2 = 7.5
would change to
24 ÷ (-3.2) = -7.5 OR
Positive ÷ negative = negative
(And this goes with any operation)
What will 2(x-4) simplify to?
Answers
Answer:
2x-8
Step-by-step explanation:
Answer:
2x-8
Step-by-step explanation:
If your doing distributive property then you multiply the 2 by the x and the 8 which will give you
2x-8
80 points please help

Answers
Answer:
216
Step-by-step explanation:
gof(6) means g(f(6))
f(6)=2(6)-6=6
g(6)=6^3=216
Use the following statements to write a compound
statement for the disjunction -p or -q. Then find its truth
value.
p: There are 14 inches in 1 foot.
q: There are 3 feet in 1 yard.
Answers
The disjunction of -p or -q can be written as (-p) v (-q). So, we have to find the truth value of (-p) v (-q). So, the compound statement for the disjunction of -p or -q is (-p) v (-q), and its truth value is true.
using the following statements: p: There are 14 inches in 1 foot.
q: There are 3 feet in 1 yard.
Solution: We know that 1 foot = 12 inches, which means that there are 14 inches in 1 foot can be written as 14 < 12. But this statement is false because 14 is not less than 12. Therefore, the negation of this statement is true, which gives us (-p) as true.
Now, we know that 1 yard = 3 feet, which means that there are 3 feet in 1 yard can be written as 3 > 1. This statement is true because 3 is greater than 1. Therefore, the negation of this statement is false, which gives us (-q) as false.
Now, we can use the values of (-p) and (-q) to find the truth value of (-p) v (-q) using the disjunction rule. The truth value of (-p) v (-q) is true if either (-p) or (-q) is true or both (-p) and (-q) are true. Since (-p) is true and (-q) is false, the disjunction of (-p) v (-q) is true. Hence, the compound statement for the disjunction of -p or -q is (-p) v (-q), and its truth value is true.
For more questions on: compound statement
https://brainly.com/question/28794655
#SPJ8
What is the measurement of the angle shown below?
A. 120
B. 60
C. 30
D. 180

Answers
Answer:
120°
Hope it helped you
₹7,000 is borrowed at 3.5% rate of interest p.a. borrowed for 2 years. Find the
amount to be paid at the end of the second year
Answers
Hope this helps (:

Evaluate the following by writing it as a difference of two squares first:
103^2 − 97^2
Answers
Answer:
1200
Step-by-step explanation:
A difference of 2 squares factors in general as
a² - b² = (a - b)(a + b) , then
103² - 97²
= (103 - 97)(103 + 97)
= 6 × 200
= 1200
The correct answer is 1200.
What is the difference between two squares called?Where one perfect square is subtracted from another, is called a difference of two squares. It arises when (a − b) and (a + b) are multiplied together. This is one example of what is called a special product.
A difference of 2 squares factors in general is written as
a² - b² = (a - b)(a + b) , then
103² - 97²
= (103 - 97)(103 + 97)
= 6 × 200
= 1200
Learn more about the difference of 2 squares here https://brainly.com/question/3189867
#SPJ2
find the order of the matrix product ab and the product ba, whenever the products exist. a is 4 x 2, b is 2 x 4.A) AB is 2 x 2, BA is 4 x 4. B) AB is nonexistent, BA is 2x2. C) AB is 4 x 4, BA is nonexistent. D) AB is 4 x 4, BA is 2 x 2
Answers
The correct answer is (D) AB is 4 x 4, BA is 2 x 2.
What is order of a matrix?
The order of a matrix refers to the number of rows and columns in the matrix. If a matrix has m rows and n columns, we say that it is an m x n matrix. The order of the matrix is written as "m x n".
In general, if A is an m x n matrix and B is an n x p matrix, then the product AB is an m x p matrix and the product BA is an n x n matrix.
In this case, A is a 4 x 2 matrix and B is a 2 x 4 matrix. Therefore, the product AB is a 4 x 4 matrix, and the product BA is a 2 x 2 matrix.
So the answer is (D) AB is 4 x 4, BA is 2 x 2.
To learn more about order of a matrix, visit the link:
https://brainly.com/question/31373779
#SPJ4
Keitaro walks at a pace of 3 miles per hour and runs at a pace of 6 miles per hour. Each month, he wants to complete at least 36 miles but not more than 90 miles. The system of inequalities represents the number of hours he can walk, w, and the number of hours he can run, r, to reach his goal. What are the two inequalities in this system
Answers
The two inequalities in the system for Keitaro to reach his monthly goal of at least 36 miles but not more than 90 miles are: 3w + 6r ≥ 36 and 3w + 6r ≤ 90, where w represents the number of hours he walks and r represents the number of hours he runs.
To form the inequalities, we need to consider the distances covered by Keitaro while walking and running, as well as the minimum and maximum monthly goals.
Let's start with the minimum goal of 36 miles. We know that the walking pace is 3 miles per hour. Therefore, the distance covered by walking can be expressed as 3w, where w represents the number of hours Keitaro walks. Similarly, the distance covered by running can be expressed as 6r, where r represents the number of hours he runs.
To reach at least 36 miles, the total distance covered (3w + 6r) must be greater than or equal to 36. Hence, the first inequality is 3w + 6r ≥ 36.
Now let's consider the maximum goal of 90 miles. To ensure that the total distance covered is not more than 90 miles, the second inequality is 3w + 6r ≤ 90.
Therefore, the system of inequalities is 3w + 6r ≥ 36 and 3w + 6r ≤ 90, where w represents the number of hours Keitaro walks and r represents the number of hours he runs. These inequalities ensure that Keitaro's monthly distance falls within the desired range of at least 36 miles but not exceeding 90 miles.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ11
I need the answer and maybe someone can tell me how to do it? Please and Thanks!! :))
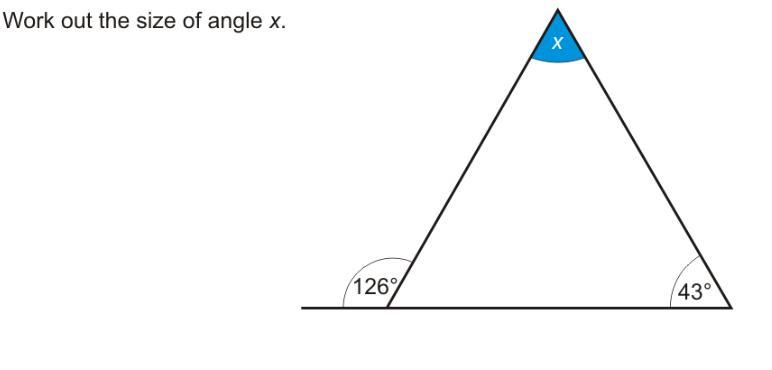
Answers
Answer:
83
Step-by-step explanation:
The 126 angle is an exterior angle of the triangle.
The 43 and x angles are the two remote interior angles of the 126 angle.
Theorem:
The measure of an exterior angle of a triangle equals the sum of the measures of the remote interior angles.
x + 43 = 126
x = 83
Answer:
x = 83
Step-by-step explanation:
The exterior angle of a triangle is equal to the sum of the opposite interior angles
126 = x+43
Subtract 43 from each side
126-43 = x+43-43
83 = x
Tick the calculations that would increase 275 by 10%.
A 275 + 10
B
110
x 275
100
С
10
x 275
100
D 275 + 27.5
Answers
Answer:
D & B
Step-by-step explanation:
Mike deposits $145 in his savings account. Each week after that, he deposits $15. How much is in Mike's account during week 6?
Answers
Answer:235
Step-by-step explanation:i got it right on test
Solve for x. Enter the solutions from least to greatest.
(x + 7)² - 49 = 0
lesser x =
greater x =
Answers
Answer:
Lesser x = -14
Greater x = 0
Step-by-step explanation:
Given equation:
\(\sf (x+7)^2-49=0\)
Add 49 to both sides:
\(\implies \sf (x+7)^2-49+49=0+49\)
\(\implies \sf (x+7)^2=49\)
Square root both sides:
\(\implies \sf \sqrt{(x+7)^2}=\sqrt{49}\)
\(\implies \sf x+7=\pm7\)
Solve for x:
\(\implies \sf x+7=7 \implies x=0\)
\(\implies \sf x+7=-7 \implies x=-14\)
As -14 < 0
Lesser x = -14Greater x = 0do you compare a negative decimal to a positive decimal?
Answers
Answer:
Positive: Decimals are a part of a whole just like fractions are a part of a whole. Therefore, a positive decimal is always greater than a negative decimal.
Negative: When you have two negative decimals, the one closer to zero is always greater. The farther a negative decimal is from zero, the smaller its value.
All of it put together (same text as above):
Decimals are a part of a whole just like fractions are a part of a whole. Therefore, a positive decimal is ALWAYS greater than a negative decimal. When you have two negative decimals, the one closer to zero is always greater. The farther a negative decimal is from zero, the smaller its value.
Consider the upper bound for total numerical error E h2 eh) + M h 6 Prove that e(h) has a minimum at h = : 3€/M
Answers
To prove that e(h) has a minimum at h = 3€/M, we need to first understand the terms involved. The upper bound for total numerical error E h2 eh) + M h 6 refers to the maximum possible error in a numerical computation.
It includes two types of error: the truncation error (E h2) which results from approximating a mathematical function using a finite number of terms, and the round-off error (eh) which results from the limited precision of computer arithmetic.
The numerical error e(h) is a function of the step size h used in numerical approximations. It is given by e(h) = E h2 + M h 6 + eh.
Now, to prove that e(h) has a minimum at h = 3€/M, we can take the derivative of e(h) with respect to h and set it to zero.
de(h)/dh = 2Eh - Mh5 + eh'
Setting this equal to zero, we get:
2Eh - Mh5 + eh' = 0
Rearranging and solving for h, we get:
h = (2E/Me')^(1/4)
Substituting this value of h in e(h), we get:
e(h) = (4/3)^(3/4) * (EM)^(1/4) * eh'
Since eh' is a constant, e(h) is minimized when EM is minimized.
Therefore, we need to find the minimum value of EM, which is achieved when h = 3€/M.
Thus, we can conclude that e(h) has a minimum at h = 3€/M.
Visit here to learn more about numerical computation:
brainly.com/question/29555380
#SPJ11
The roots of the quadratic function are -2 and -6.Which of the following are the two factors of the quadratic expression?X + 2X-2X - 6X + 6X + 8X - 8
Answers
roots = {-2, -6}
Factors: (x + 6) and (x + 2)
A surveyor is 40m from the edge of a building. The angle of elevation from the surveyor to the top of the building is 55° . What is the height of the building?
Answers
Answer:
Height of building is 57.12 m.
Step-by-step explanation:
Let us try to understand the given dimensions as per the attached diagram.
Please refer to attached image (Right angled \(\triangle OBT\))
with \(\angle B =90^\circ\)
Let O be the point where the Surveyor is standing.
B be the point of the base of building.
T be the point of top of building.
As per question statement,
\(\angle O = 55^\circ\)
Side OB = 40 m
To find: Side BT = ?
Using tangent trigonometric identity:
\(tan\theta =\dfrac{Perpendicular}{Base}\)
\(tanO =\dfrac{BT}{BO}\\\Rightarrow tan55^\circ = \dfrac{BT}{40}\\\Rightarrow BT = tan55^\circ \times 40\\\Rightarrow BT = 1.43\times 40\\\Rightarrow BT = 57.12 m\)
So, height of building is 57.12 m.

Please I need some answer only a few is fine

Answers
Answer:
a) 64
b) 9
c) 1
d) 49
Step-by-step explanation:
8^2 = 64
same as 8*8
1^2 = 1
same as 1*1
3^2 = 9
same as 3*3
7^2 = 49
same as 7*7
a: 64, b:9, c:1, d:49
Step-by-step explanation:
because 8 squared is 64, 3 squared is 9(3×3=9), 1 squared is 1(1×1), and 7 squared is 49.
Which side is the smallest?

Answers
Answer:
WX
Step-by-step explanation:
The distance between vertex X and vertex W is much smaller then from X to Y or W to Y.
- there is a theorem but i can't remember the name but it basically says if you have a triangle and have all three angles you can tell the sides and the side lengths by the angle.
- so angle y is 27 degrees so the opposite side of that angle is the shortest side since it is the smallest angle
- angle x is 92 degrees so the opposite side would be the largest side since it is the largest angle.
i hope this helps you!
4 Gina drew three small congruent circles
beside one large circle.
2 cm
Based on the diagram, which answer
choice is closest to the area of the large
circle?
F 28.3 cm?
H 18.8 cm?
G 12.6 cm? J 24.4 cm?
7.9B
Answers
Answer:
c
Step-by-step explanation:
find the points on the ellipse 3x2 2y2=1 where f(x,y)=xy has its extreme values.
Answers
The extreme values of f(x, y) = xy occur at the points (2, 1) and (-2, -1) on the ellipse \(3x^{2} +2y^{2} =1\).
To find the extreme values of f(x, y) = xy on the ellipse \(3x^{2} +2y^{2} =1\), we can use the method of Lagrange multipliers.
Define the function g(x, y) = \(3x^{2} +2y^{2} -1\). We need to find points (x, y) where the gradient of f is proportional to the gradient of g:
∇f = λ∇g
The gradient of f is ∇f = (y, x), and the gradient of g is ∇g = (6x, 4y). Therefore, we have the following system of equations:
y = 6λx
x = 4λy
Substitute the second equation into the first:
y = 6λ(4λy)
y = \(24λ^{2y}\)
If y ≠ 0, then 1 = \(24λ^{2}\), and λ = ±1/2. Plugging this value into the second equation gives x = ±2. Thus, we have two potential extreme points: (2, 1) and (-2, -1).
Now consider the case when y = 0. The constraint equation becomes \(3x^{2} =1\), and x = ±1/√3. However, these points correspond to f(x, y) = 0, which is not an extreme value.
Therefore, the extreme values of f(x, y) = xy occur at the points (2, 1) and (-2, -1) on the ellipse \(3x^{2} +2y^{2} =1\).
Know more about Extreme values here:
https://brainly.com/question/29667439
#SPJ11
Use a Riemann sum with 4 rectangles of equal width to approximate the area between y=3x^(2)+1 and the x-axis on the interval -1,5. Use the left -hand endpoint of each subinterval.
Answers
The approximate area between y=3x^(2)+1 and the x-axis on the interval -1 to 5 is 136.6875.
We can approximate the area between y=3x^(2)+1 and the x-axis on the interval -1 to 5 using a Riemann sum with 4 rectangles of equal width. The left-hand endpoint of each subinterval will be used.
The width of each rectangle is the length of the interval (5-(-1)) divided by the number of rectangles (4). Therefore, the width of each rectangle is
(5-(-1))/4 = 6/4 = 1.5.
Since we are using the left-hand endpoint of each subinterval, the x-values of the left-hand endpoints of the rectangles are
-1, -1+1.5
-1+1.5+1.5
-1+1.5+1.5+1.5 = -1+4.5=3.5
The height of each rectangle is determined by the value of y at the corresponding x-value.
Therefore, the heights of the rectangles are
3(-1)^2+1=2
3(-1+1.5)^2+1=7.125
3(3.5)^2+1=35.125
3(3.5+1.5)^2+1=46.875
The area of each rectangle is the product of its width and height, so the areas of the rectangles are
2*1.5=3
7.125*1.5=10.6875
35.125*1.5=52.6875
46.875*1.5=70.3125.
Therefore, the approximate area between y=3x^(2)+1 and the x-axis on the interval -1 to 5 is 136.6875.
Learn more about Riemann sum here:
https://brainly.com/question/28969415
#SPJ4
Which function is a quadratic function?
O p(x) = 2x(x2 + 6) + 1
m(x) = -4(x + 3) - 2
Ot(x) = -8x²(x2 – 6) + 1
Oh(x) = 3x(x - 2) - 4
Answers
What is the value of the expression below?
-8 + 19 + 8
0
11
19
35
Answers
Answer:
19
Step-by-step explanation:
-8+8=0
0+19=19
Hope it helps.
Answer:
19
Step-by-step explanation:
I just took the quiz