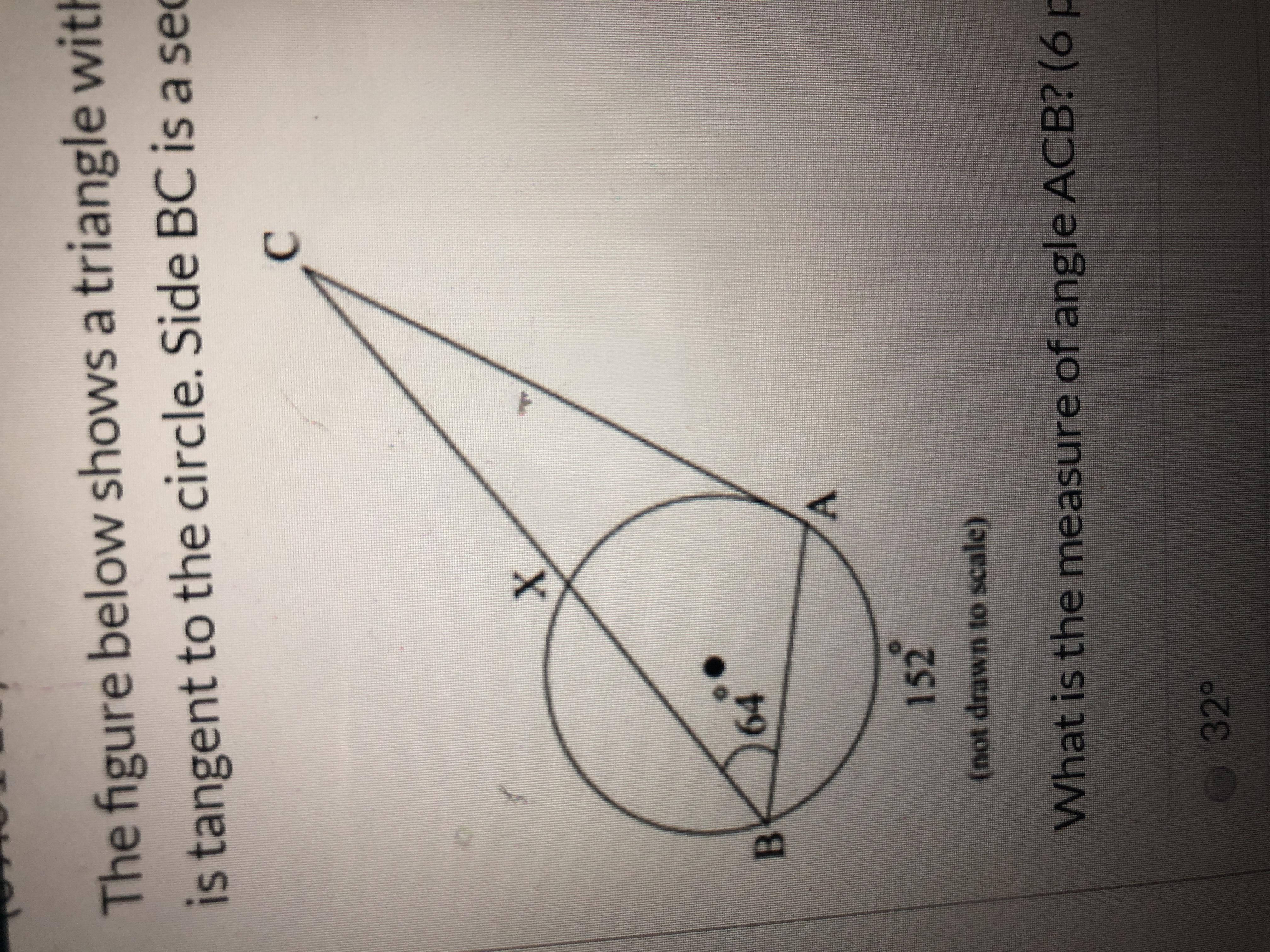
The Figure below shows a triangle with vertices a and B on a circle and vertex C outside it Side AC is tangent to the circle side BC is a sink and intersecting the circle at point X what is the measure of angle ACB

32
6
24
12

Solution

We want to graph the parabola

To find the vertex, We will equate

Coordinate of the vertex is (-2, -5)

To the left of the vertex, let us pick x = -3 and x = -5

when x = -3

Coordinate is (-3, -6)

When x = -5

Coordinate is (-5, -14)

To the right of the vertex

We can pick x = 0 and x = 1

W

EXPLANATION

Replacing the given functions into the following:

Removing the parentheses and simplifying:

Simplifying like terms:

Hence,

The required, 68.2 divided by 0.4 is equal to quotient 170.5, as per the given condition.

In mathematics, it deals with numbers of operations according to the statements. There are four major arithmetic operators, addition, subtraction, multiplication, and division,

Here,
68.2 divided by 0.4 is given as,

To divide a decimal value by another decimal value, you can use the same process as dividing whole numbers, but you need to make sure that the decimal points are lined up correctly.

= 68.2 / 0.4

= 682/4
= 170.5

Therefore, 68.2 divided by 0.4 is equal to 170.5.

Learn more about arithmetic here:

https://brainly.com/question/29111583
#SPJ9

Answer:  A

Step-by-step explanation:

Benny's Pizza

13.60 + 2.50(3)

13.60 + 7.50

21.10

Ricco's Pizza

14.60 + 2(3)

14.60 + 6

21.60

Answer:

TV = 9.71

Step-by-step explanation:

sin 47° = TV/13.28

0.7314 = TV/13.28

TV = 9.71

Using a t-distribution with 14 degrees of freedom (n-1) and a 98% confidence level (α = 0.02/2 = 0.01 for each tail), we have:

sample mean (x) = (2051+2061+2162+2167+2169+2171+2180+2183+2186+2195+2196+2198+2205+2210+2211)/15 = 2180.6

sample standard deviation (s) = 39

standard error of the mean (SEM) = s/√n = 39/√15 ≈ 10.077

t-score for a 98% confidence level and 14 degrees of freedom (from t-distribution table or calculator) = 2.977

Margin of error (ME) = t-score × SEM = 2.977 × 10.077 ≈ 30.05

Therefore, the 98% confidence interval for the mean hours worked per year in this state is:

(x- ME, x+ ME) = (2180.6 - 30.05, 2180.6 + 30.05) = (2150, 2211)

Rounding to the nearest integer and putting the limits in ascending order, we get:

(2150, 2211)

Visit here to learn more about confidence level brainly.com/question/22851322

#SPJ11

Answer:

A. -20p - 2

General Formulas and Concepts:

Pre-Algebra

Algebra I

Step-by-step explanation:

Step 1: Define

2 - 4(5p + 1)

Step 2: Simplify

Answer:

Step-by-step explanation:

Apply the distributive property

2-20p-4

Simplify expression

-20p-2

Answer choice A is correct

Answer:

15

Step-by-step explanation:

Since the angles are complementary, that means that when the angles are added together, they are equal to 90*. With this information, we can make the equation: x + (3x + 30) = 90

From this we can add like terms and get 4x + 30 = 90

After this, subtract 30 from both sides: 4x = 60

Divide both sides by 4

x = 15

(Ignore the degree sign in my picture, sorry!)

17j+7 is the algebraic expression for Seven more than the product of 17 and Julie's savings.

Expression is a combination of variables, operators and numbers.

The given phrase is

"Seven more than the product of 17 and Julie's savings"

and j is variable to represent Julie's savings.

In the phrase we have Seven more than, it means we are adding 7 to something.

According to problem we are adding 7 to "product of 17 and Julie's savings"

Product means multiplying a number with another factor. Here the factor is julies saving j.

17j+7 is the translated algebraic expression.

Hence 17j+7 is the translation of  Seven more than the product of 17 and Julie's savings.

To learn more on expressions click:

https://brainly.com/question/14083225

#SPJ1

The piece of meat has a weight of 1,800g.

So, as the question says allow 30 minutes of cooking to each 450g.

Similarly,

Therefore, the piece of meat has a weight of 1,800g.

Know more about mathematical operations here:

brainly.com/question/28294142

#SPJ9

Answer:

1800

Step-by-step-explanation:

The aquarium with dimensions 16 in. × 8 in. × 10 in. can hold approximately 30.6 liters of water and approximately 8.09 gallons.

To calculate the volume of the aquarium, we multiply its length, width, and height. Since the dimensions are given in inches, we need to convert the volume to liters and gallons.

First, let's calculate the volume in cubic inches:

Volume = Length × Width × Height = 16 in. × 8 in. × 10 in. = 1280 cubic inches.

To convert cubic inches to liters, we divide the volume by 61.024:

Volume in liters = 1280 in³ / 61.024 = 20.96 liters (rounded to two decimal places).

To convert liters to gallons, we divide the volume by 3.78541:

Volume in gallons = 20.96 liters / 3.78541 = 5.53 gallons (rounded to two decimal places).

Therefore, the aquarium can hold approximately 30.6 liters of water and approximately 8.09 gallons.

Learn more about dimensions here:

https://brainly.com/question/31106945

#SPJ11

Answer:

True

Step-by-step explanation:

If the coefficient of determination is 0.94, we can say that ninety-four percent of the total variation of the dependent variable is explained by the independent variable. The correct answer is: ninety-four percent of the total variation of the dependent variable is explained by the independent variable.

This means that there is a strong positive relationship between the two variables. The coefficient of determination, represented as R², measures the proportion of the total variation in the dependent variable that is explained by the independent variable. In this case, an R² of 0.94 indicates that 94% of the total variation in the dependent variable can be explained by the independent variable. The coefficient of determination does not provide information about the direction or strength of the relationship. The correct answer therefore is ninety-four percent of the total variation of the dependent variable is explained by the independent variable.

More on coefficient of determination: https://brainly.com/question/28975079

#SPJ11

The z-score for which the area under the standard normal curve to its left is 0.96 is approximately 1.75.

What is a normal distribution?

A normal distribution is a type of probability distribution that is often used in statistical analysis. It is a continuous probability distribution that is symmetric around its mean and bell-shaped, with the majority of the data points falling close to the mean and fewer data points farther away from the mean.

We can use a standard normal distribution table or a calculator to find the z-score that corresponds to a left-tail area of 0.96.

Using a standard normal distribution table, we look for the row corresponding to 0.9 in the left-hand column and the column corresponding to 0.06 in the top row. The intersection of these rows and columns gives us a value of 1.75. This means that the area to the left of z = 1.75 under the standard normal curve is approximately 0.96.

Alternatively, we can use a calculator that has a built-in function to calculate the inverse cumulative distribution function (also called the inverse normal function) to find the z-score. For example, using the qnorm() function in R, we can compute:

qnorm(0.96)

which gives us a value of approximately 1.75.

Therefore, the z-score for which the area under the standard normal curve to its left is 0.96 is approximately 1.75.

To learn more about normal distribution from the given link:

https://brainly.com/question/29509087

#SPJ1

Answer:

b.rests

Step-by-step explanation:

HOPE IT'S HELP

#PHILIPPINES

Answer:

x = \(\frac{5}{8}\)

Step-by-step explanation:

Given

- 4(3 + x) + 5 = 4(x + 3) ← distribute parenthesis on both sides

- 12 - 4x + 5 = 4x + 12 , that is

17 - 4x = 4x + 12 ( subtract 4x from both sides )

17 - 8x = 12 ( subtract 17 from both sides )

- 8x = - 5 ( divide both sides by - 8 )

x = \(\frac{-5}{-8}\) = \(\frac{5}{8}\)

Answer:

4r^3+8r^2-5r-10

= 4r^2(r+2)-5(r+2) [Factorise out like terms; distributive law of multiplication to check]

=(4r^2-5)(r+2) [Combine expressions]

  El 1 y el 20 no se consideran para formar grupos debido a que tienen una propiedad especial en común. El número 1 es un elemento neutro en la multiplicación y el número 20 es un múltiplo común para todos los números del 1 al 20.

  Por lo tanto, cualquier grupo que incluya 1 no afectará la multiplicación de los otros números del grupo y cualquier grupo que incluya 20 siempre tendrá un múltiplo común que lo hace irrelevante para la agrupación.

  De esta manera, se evita la redundancia y se maximiza la eficiencia en la formación de grupos al resolver problemas de matemáticas o estadísticas.

According to the values in the table, no, x and y does not have a proportional relationship. Therefore, the correct answer option is: B. no.

In Mathematics, a proportional relationship is a type of relationship that generates equivalent ratios and it can be modeled or represented by the following mathematical expression:

y = kx

Where:

Next, we would determine the constant of proportionality (k) for the relationship between the x-values and y-values in this table as follows:

Constant of proportionality, k = y/x

Constant of proportionality, k = 93/1.1 ≠ 95/1.3 ≠ 98/1.6 ≠ 100/1.8

Since the constant of proportionality (k) for the relationship between the x-values and y-values are different, we can logically deduce that this is not a proportional relationship.

Read more on proportional relationship here: brainly.com/question/20167968

#SPJ1

FINDING THE DIFFERENCE WE SUBRACT

\(8 - 4 \\ = 4\)

FINDING THE QUOTIENT WE DIVIDE

\(8 \div 4 \\ = 2\)

HOPE THIS HELPS

The only function whose range includes all real values and is both odd and even is the constant function f (x) = 0, which is precisely zero.

The constant function that is precisely zero, f (x) = 0, is the only function whose range encompasses all real values and is both odd and even. When two functions are added together, they are either even or odd.

F(x) = 0, which is defined for all real numbers, is the unique function that is both even and odd. This is merely a line that is located on the x-axis. A function that is even is the result of two even functions. An even function is the result of two odd functions. An odd function is created when an even function and an odd function are combined.

Neither an even nor an odd function is a function f(x) in which f(x) ≠ f(−x) and −f(x) ≠ f(−x) for any value of x. These functions aren't symmetrical either about the origin or the y-axis on a graph.

To learn more about function refer to;

https://brainly.com/question/11624077

#SPJ4

Answer: The value Tₙ of the machine after n years using flat rate depreciation is Tₙ = $4620 - $385n.

Step-by-step explanation:

To determine the value of the machine after a given number of years using flat rate depreciation, we need to find the common difference in value per year.

Let's denote the initial value of the machine as V₀ and the common difference in value per year as D. We are given the following information:

After 5 years, the value of the machine is $2695.

After a further 7 years, the value becomes $0.

Using this information, we can set up two equations:

V₀ - 5D = $2695    ... (Equation 1)

V₀ - 12D = $0      ... (Equation 2)

To solve this system of equations, we can subtract Equation 2 from Equation 1:

(V₀ - 5D) - (V₀ - 12D) = $2695 - $0

Simplifying, we get:

7D = $2695

Dividing both sides by 7, we find:

D = $2695 / 7 = $385

Now, we can substitute this value of D back into Equation 1 to find V₀:

V₀ - 5($385) = $2695

V₀ - $1925 = $2695

Adding $1925 to both sides, we get:

V₀ = $2695 + $1925 = $4620

Therefore, the initial value of the machine is $4620, and the common difference in value per year is $385.

To find the value Tₙ of the machine after n years, we can use the formula:

Tₙ = V₀ - nD

Substituting the values we found, we have:

Tₙ = $4620 - n($385)

So, To determine the value of the machine after a given number of years using flat rate depreciation, we need to find the common difference in value per year.

Let's denote the initial value of the machine as V₀ and the common difference in value per year as D. We are given the following information:

After 5 years, the value of the machine is $2695.

After a further 7 years, the value becomes $0.

Using this information, we can set up two equations:

V₀ - 5D = $2695    ... (Equation 1)

V₀ - 12D = $0      ... (Equation 2)

To solve this system of equations, we can subtract Equation 2 from Equation 1:

(V₀ - 5D) - (V₀ - 12D) = $2695 - $0

Simplifying, we get:

7D = $2695

Dividing both sides by 7, we find:

D = $2695 / 7 = $385

Now, we can substitute this value of D back into Equation 1 to find V₀:

V₀ - 5($385) = $2695

V₀ - $1925 = $2695

Adding $1925 to both sides, we get:

V₀ = $2695 + $1925 = $4620

Therefore, the initial value of the machine is $4620, and the common difference in value per year is $385.

To find the value Tₙ of the machine after n years, we can use the formula:

Tₙ = V₀ - nD

Substituting the values we found, we have:

Tₙ = $4620 - n($385)

So, the value Tₙ of the machine after n years using flat rate depreciation is Tₙ = $4620 - $385n.

Learn more about depreciation:https://brainly.com/question/1203926

#SPJ11

If a scatterplot of standardized, bivariate data displays data that are mostly lying in the upper left and lower right-hand quadrants, then the Pearson correlation is typically going to be negative. The above statement is false.

Bivariate data involves studying and comparing two separate variables. For example, a researcher may record how long it takes people to complete a crossword puzzle while measuring the stress levels of the participants. In this example, the two variables that the researcher is examining are time and stress.

Scatterplots display these bivariate data sets and provide a visual representation of the relationship between variables. In a scatterplot, each point represents a paired measurement of two variables for a specific subject, and each subject is represented by one point on the scatterplot.

When the points on a scatterplot graph produce a lower-left-to-upper-right pattern, we say that there is a positive correlation between the two variables. This pattern means that when the score of one observation is high, we expect the score of the other observation to be high as well, and vice versa.

When the points on a scatterplot graph produce a upper-left-to-lower-right pattern, we say that there is a negative correlation between the two variables. This pattern means that when the score of one observation is high, we expect the score of the other observation to be low, and vice versa.

In statistics, the Pearson correlation coefficient ― also known as Pearson's r, the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).

The Pearson correlation method is the most common method to use for numerical variables; it assigns a value between − 1 and 1, where 0 is no correlation, 1 is total positive correlation, and − 1 is total negative correlation. This is interpreted as follows: a correlation value of 0.7 between two variables would indicate that a significant and positive relationship exists between the two. A positive correlation signifies that if variable A goes up, then B will also go up, whereas if the value of the correlation is negative, then if A increases, B decreases.

Learn more about Pearson Correlation:

https://brainly.com/question/15353989

#SPJ4

Answer:

Step-by-step explanation:

\(\sqrt{\frac{36}{100} } \\\\\sqrt{36} =6\\\sqrt{100} =10\\\\=\frac{6}{10}\\\\Simplify\\\\6\div 2=3\\10\div 2 =5\\\\\frac{3}{5}\)

Answer:

To solve the inequality -18x + 9 > 9 for x, you need to isolate the variable x on one side of the inequality symbol. Here's how to do it:

First, subtract 9 from both sides of the inequality:

-18x + 9 - 9 > 9 - 9

Simplify:

-18x > 0

Next, divide both sides of the inequality by -18, remembering to reverse the direction of the inequality symbol because you are dividing by a negative number:

x < 0/(-18)

x < 0

Therefore, the solution to the inequality -18x + 9 > 9 is x < 0.

Answer:

x<0

Step-by-step explanation:

First you want to isolate -18x.

-18x > 0

That means -18x is greater than 0

Then we have to divide -18 by both sides and we need to flip the relation because the factor is negative.

x<0/-18

x<0

Answer:

x=4 y=5

Step-by-step explanation:

Answer:

It’s b

Step-by-step explanation

Answer: B

Step-by-step explanation:

Answer: 6 years

Step-by-step explanation:

Formula to calculate compound amount: \(A=P(1+r)^t\), where P= Principal , r=rate of interest, t= time

Given: P = £400, r = 3% = 0.03 , A= 475

Required equation: \(400(1+0.03)^t\geq475\)

\(400(1.03)^t\geq475\\\\\Rightarrow\ (1.03)^t\geq\dfrac{475}{400}\\\\\Rightarrow\ (1.03)^t\geq1.1875\)

Taking log on both sides , we get

\(t \log 1.03\geq\log1.1875\\\\\Rightarrow\ t(0.0128372)\geq(0.0746336)\\\\\Rightarrow\ t\geq\dfrac{0.0746336}{0.0128372}=5.81385\approx6\)

Hence, he needs to invest the money for 6 years to get atleast £475.