The equation of a circle is given below. (x-0.5)^{2}+(y-3.5)^{2} = 16(x−0.5) 2 +(y−3.5) 2 =16left parenthesis, x, minus, 0, point, 5, right parenthesis, squared, plus, left parenthesis, y, minus, 3, point, 5, right parenthesis, squared, equals, 16 What is its center? ((left parenthesis ,,comma ))right parenthesis What is its radius? If necessary, round your answer to two decimal places. units
Answers
Answer:
The radius is 4 units long.Step-by-step explanation:
The given equation is
\((x-0.5)^{2} +(y-3.5)^{2} =16\)
This equation belongs to a circle, which center is at (0.5, 3.5) and its radius is 4.
You can deduct its elements, becase this equation of the circle is explicit, which means the constant term represents the square power of the radius. Solving that, we have
\(r^{2} = 16\\r=\sqrt{16}\\ r=4\)
Therefore, the radius is 4 units long.
Related Questions
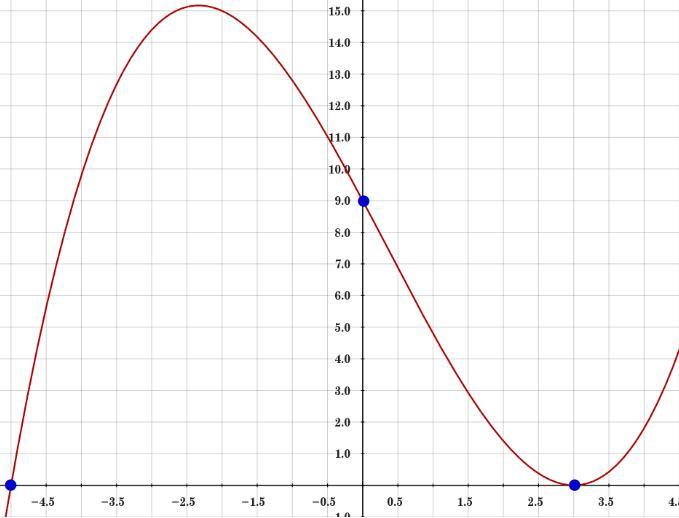
Find a polynomial function f(x) of least possible degree having the graph shown

Answers
first off let's notice a few things on that function.
the graph "passes" -5, that's a root, the graph "touches" 3 and goes back up, that's another root, but that's a root with an "even multiplicity", the heck does that mean? well, it means there are at least two roots, could be 4 or 6 or 18, so long is even, but we're shooting for the least degree, so we'll settle for 2.
now hmm, let's reword that
what's the equation of a function with roots at -5 and 3 twice, that it passes through (0 , 9)?
\(\begin{cases} x = -5 &\implies x +5=0\\ x = 3 &\implies x -3=0\\ x = 3 &\implies x -3=0\\ \end{cases} \\\\[-0.35em] ~\dotfill\\\\ \stackrel{original~polynomial}{a ( x +5 )( x -3 )( x -3 ) = \stackrel{0}{y}}\hspace{5em}\textit{we also know that } \begin{cases} x=0\\ y=9 \end{cases} \\\\\\ a ( 0 +5 )( 0 -3 )( 0 -3 ) = 9\implies 45a=9\implies a=\cfrac{9}{45}\implies a=\cfrac{1}{5} \\\\[-0.35em] ~\dotfill\)
\(\cfrac{1}{5}(x+5)(x-3)^2=y\implies \cfrac{1}{5}(x+5)(x^2-6x+9)=y \\\\\\ \cfrac{1}{5}(x^3-x^2-21x+45)=y\implies {\Large \begin{array}{llll} \cfrac{x^3}{5}-\cfrac{x^2}{5}-\cfrac{21x}{5}+9=y \end{array}}\)
Check the picture below.
The box plot represents the distribution of the number of points scored by a cross country team at 12 meets.
22 24 26 28 30 32 34 36 38 40 42
points
If possible, find the mean. If not possible, explain why not.
Answers
Answer:It is not possible
Step-by-step explanation: It is not possible because we need 12 plot to solve for an accurate mean but there is only 11 data which is impossible.
If f(x) = -2x + 4, then f-1(x) =
Answers
if the volume of a ball is 32,490 cubic millimeters, what is the volume of the ball in cubic centimeters?
Answers
The volume of ball is 32.49 cubic centimeter.
What is volume ?
Every three-dimensional item takes up space in some way. The volume of this area is what is used to describe it. The area occupied within an object's three-dimensional bounds is referred to as its volume. The object's capacity is another name for it.
Here ,
The volume of a ball = 32490 cubic millimeters
To convert into cubic millimeter into cubic centimeter by dividing by 1000, Then,
=> 32490/1000
=> 32.49 cubic centimeter.
Hence the volume of ball in cubic centimeter is 32.49 .
To learn more about volume
https://brainly.com/question/14197390
#SPJ4
Given J(x, -8) and K(-1, -5) and the graph
of l line I below, find the value of x so that
JK || l.

Answers
The value of x for which the points j(x, -8) and K(-1, -5) is parallel to the line l is -2
What is an intercept?An intercept is any point on the graph where the line or curve touches the x or y axes.
If the intercept is on the y-axis the coordinate of x is 0 and if the intercept is on the x-axis the coordinate of y is 0.
For the line l, the coordinates of the marked points are (0, 2) and (-2, -4)
The slope of the line is \(\frac{y_{2} - y_{1} }{x_{2} - x_{1} }\)
\(x_{1}\) = 0, \(x_{2}\) = -2 , \(y_{1}\) = 2, \(y_{2}\) =-4
Slope of the line = -4 -2 / -2 - 0
slope = -6/-2
slope(P) = 3
slope(R) for the line formed by the two points J(x, -8) and K(-1, -5)
R = -5 - -8 / -1 -x
R = 3/-1 -x
For two parallel lines, their slopes are equal, that is
R = P
3/-1 -x = 3
By cross multiplying
3(-1 -x) = 3
-3 -3x = 3
-3x = 3 + 3
-3x = 6
x = 6/-3
x = -2
In conclusion, the value of x for which JK // l is -2
Learn more about parallel lines: https://brainly.com/question/26961508
#SPJ1
An Arrow-Debreu security pays $1 at expiry node (6,2). The upstate risk neutral probability is π=0.4 and the return over one time-step is R=1.05. What is the premium of this Arrow-Debreu security?
Answers
The value of the Arrow-Debreu security is calculated as the present value of its expected payoff, discounted at the risk-neutral rate. As a result, the premium of the Arrow-Debreu security can be computed using the following formula: \($P_{t}=\frac{1}{(1+R)^{n-t}}\times \pi$,\)
where π=0.4, R=1.05, n=6, and t=2 (expiry node).
By substituting the values, we obtain:
\($P_{2}=\frac{1}{(1+1.05)^{6-2}}\times 0.4 = \frac{0.4}{(1.05)^4} \approx 0.3058$.\)
Therefore, the premium of the Arrow-Debreu security is approximately $0.3058.
Arrow-Debreu securities are typically utilized in financial modeling to simplify the pricing of complex securities. They are named after Kenneth Arrow and Gerard Debreu, who invented them in the 1950s. An Arrow-Debreu security pays $1 if a particular state of the world is realized and $0 otherwise.
They are generally utilized to price derivatives on numerous assets that can be broken down into a set of Arrow-Debreu securities. The value of an Arrow-Debreu security is calculated as the present value of its expected payoff, discounted at the risk-neutral rate. In other words, the expected value of the security is computed using the risk-neutral probability, which is used to discount the value back to the present value.
The formula is expressed as:
\($P_{t}=\frac{1}{(1+R)^{n-t}}\times \pi$\),
where P_t is the price of the Arrow-Debreu security at time t, π is the risk-neutral probability of the security’s payoff, R is the risk-free rate, and n is the total number of time periods.However, Arrow-Debreu securities are not traded in real life. They are used to determine the prices of complex securities, such as options, futures, and swaps, which are constructed from a set of Arrow-Debreu securities.
This process is known as constructing a complete financial market, which allows for a more straightforward pricing of complex securities.
The premium of the Arrow-Debreu security is calculated by multiplying the risk-neutral probability of the security’s payoff by the present value of its expected payoff, discounted at the risk-neutral rate.
The formula is expressed as
\($P_{t}=\frac{1}{(1+R)^{n-t}}\times \pi$,\)
where P_t is the price of the Arrow-Debreu security at time t, π is the risk-neutral probability of the security’s payoff, R is the risk-free rate, and n is the total number of time periods. Arrow-Debreu securities are not traded in real life but are used to price complex securities, such as options, futures, and swaps, by constructing a complete financial market.
To know more about risk-neutral probability :
brainly.com/question/32719566
#SPJ11
how to determine if an integral is convergent or divergent
Answers
A. To determine if an integral is convergent, we analyze the function's behavior, integrability, apply integration techniques, and examine its limits, ensuring they are finite, leading to a finite result.
B. To determine if an integral is divergent, we look for infinite limits, vertical asymptotes, and erratic behavior within the integration interval, indicating the lack of a finite value for the integral.
A. To determine if an integral is convergent, we need to consider several approaches. First, we check for basic convergence criteria such as infinite limits or vertical asymptotes.
Then, we examine integrability, ensuring the function is continuous or has a finite number of discontinuities. Next, we simplify the integral using integration techniques.
Finally, we analyze the behavior of the function at infinity and apply comparison tests if necessary to establish convergence.
B. To determine if an integral is divergent, we follow a series of steps. First, we check for basic divergence criteria such as infinite limits or vertical asymptotes.
Then, we examine integrability, looking for discontinuities that prevent integration. Next, we simplify the integral using integration techniques. Finally, if the integral does not converge, it is deemed divergent.
for such more question on convergence
https://brainly.com/question/23558817
#SPJ8
In a bag there are 20 red cubes & 16 black cubes
One cube is picked at random.
What is the probability a red cube is picked?
Simplify your answer.
Answers
Answer:
I think that the probability is 5/4
Tara makes two batches of purple food coloring. The table show the number of drops of red and blue coloring she uses for each batch. Do the two batches use the same number of drops of red per drop of blue.

Answers
Given data:
The number of red drops for first batch are r=100.
The number of blue drops for first batch are b=20.
The number of red drops for second batch are r'=75.
The number of blue drops for second batch are b'=15.
The expression for the red per blue drop for first batch is,
n=r/b
Substitute the given values in the above expression.
n=100/20
=5
The expression for the red drop per blue drop of the second batch is,
n'=r'/b'
Substitute the given values in the above expression.
n'=75/15
=5
Thus, yes the ratio of red to the blue drop is same for both batches.
Question 12 3 pts If we know that the length of time it takes a college student to find a parking spot in the library parking lot follows a normal distribution with a mean of 2.5 minutes and a standard deviation of 0.75 minute, find the probability that a randomly selected college student will find a parking spot in the library parking lot in less than 3 minutes. 0.3085 0.3551 0.6915 0.7475
Answers
The probability that a randomly selected college student will find a parking spot in the library parking lot in less than 3 minutes is found as `0.7475`. Hence, the option D is correct.
The length of time it takes a college student to find a parking spot in the library parking lot follows a normal distribution with a mean of 2.5 minutes and a standard deviation of 0.75 minute.
We are supposed to find the probability that a randomly selected college student will find a parking spot in the library parking lot in less than 3 minutes.
So, we need to find `P(x < 3)` where `x` is the time taken to find a parking spot in the library parking lot.
Now, z-score will be
`z = (3 - 2.5)/0.75
= 0.67`
By looking at the z-score table, the probability that corresponds to z = 0.67 is 0.2514.
Therefore,
`P(x < 3) = P(z < 0.67)
= 0.2514 + 0.5
= 0.7514
≈ 0.7475 (approx)`
So, the correct option is `0.7475`. Hence, the answer is option D.
Know more about the standard deviation
https://brainly.com/question/475676
#SPJ11
HELPPP frenss!!! HURRY

Answers
Answer:
8
Step-by-step explanation:
When you calculate it -4/3 times is 4 so add 4 to that and you get 4. Hope this helps
Find each sum or difference
1. (4a - 5)+(3a + 6)
2. (6x + 9)+ (4x^2 - 7)
3. (6xy + 2y + 6x) + (4xy - x)
Answers
1. (4a - 5)+(3a + 6) = 7a + 1.
To solve, you simply combine the like terms (4a and 3a) to get 7a, and then combine the constants (-5 and 6) to get 1.
2. (6x + 9)+ (4x^2 - 7) = 4x^2 + 6x + 2.
To solve, you combine the like terms (6x and 4x^2) to get 4x^2 + 6x, and then combine the constants (9 and -7) to get 2.
3. (6xy + 2y + 6x) + (4xy - x) = 10xy + 2y + 6x - x = 10xy + 2y + 5x.
To solve, you combine the like terms (6xy and 4xy) to get 10xy, then combine the constants (2y and -x) to get 2y - x, and finally combine the like terms (6x and 5x) to get 11x. The final answer is 10xy + 2y + 5x.
Know more about constants here:
https://brainly.com/question/27983400
#SPJ11
How many small cubes, with a side length of 1/2 cm, will fill the larger rectangular prism below?

Answers
Answer: I believe 20 1/2 cm cubes would fit in the rectangular prism
Step-by-step explanation:
if a thin lamina with uniform density has a shape of an equilateral triangle whose side at the bottom is sitting horizontally on the -axis and the top vertex is on the -axis, then the center of mass is a point located ?
Answers
The center of mass of the thin lamina with uniform density in the shape of an equilateral triangle, whose side at the bottom is sitting horizontally on the x-axis and the top vertex is on the y-axis, is located on the y-axis at a distance of 1/3 times the height of the triangle from the origin.
The center of mass of a thin lamina is the point at which the entire mass of the lamina can be considered to be concentrated. The center of mass of an equilateral triangle is located at the intersection of its medians, which are the line segments joining each vertex to the midpoint of the opposite side.
In this case, the triangle has its bottom side sitting horizontally on the x-axis, so the midpoint of the bottom side is at x = 1/2. The height of the equilateral triangle is h = (sqrt(3)/2) times the length of one of its sides, so the height of this triangle is h = (sqrt(3)/2) times the length of the bottom side. Since the bottom side is sitting on the x-axis, its length is equal to the x-coordinate of the top vertex.
Therefore, the coordinates of the top vertex of the triangle are (x, y) = (h/sqrt(3), h). The medians of the triangle are the lines passing through the vertices and the midpoints of the opposite sides. The median passing through the top vertex has equation x = h/sqrt(3), while the median passing through the midpoint of the bottom side has equation y = (sqrt(3)/2)x.
The intersection of these medians is the center of mass of the triangle. Substituting x = h/sqrt(3) into the equation for the median passing through the midpoint of the bottom side, we get y = (sqrt(3)/2)(h/sqrt(3)) = h/2. Therefore, the center of mass is located at the point (h/sqrt(3), h/2).
Since the top vertex of the triangle is located at (h/sqrt(3), h), the distance between the origin and the center of mass is the y-coordinate of the center of mass, which is h/2. Therefore, the center of mass is located on the y-axis at a distance of h/2 from the origin. Substituting h = (sqrt(3)/2) times the length of the bottom side, we get the distance of the center of mass from the origin as (sqrt(3)/4) times the length of the bottom side.
Since the bottom side is sitting on the x-axis, its length is equal to the x-coordinate of the top vertex, which is h/sqrt(3). Therefore, the distance of the center of mass from the origin is (sqrt(3)/4) times (h/sqrt(3)) = 1/4 times the height of the triangle.
However, the question asks for the distance of the center of mass from the y-axis, not the origin. Since the center of mass is located on the y-axis, its x-coordinate is 0, and the distance of the center of mass from the y-axis is the absolute value of its y-coordinate, which is h/2.
Therefore, the center of mass is located on the y-axis at a distance of 1/3 times the height of the triangle from the origin
To learn more about center of mass here:
brainly.com/question/28996108#
#SPJ11
I need help with this please

Answers
Find the slope for the line that runs through points (2,5) and (-3, 7). Write your answer as a fraction using the slash as your fraction bar.
A) 2/5
B) 5/2
C) -2/5
D) -5/2
Answers
Answer:
c.
Step-by-step explanation:
5-7 = -2
2 - -3=5
-2/5
A sample of a radioactive substance decayed to 95.5% of its original amount after a year. (Round your answers to two decimal places.) (a) What is the half-life of the substance? (b) How long would it take the sample to decay to 5% of its original amount?
Answers
(a) The half-life of the substance can be determined by finding the time it takes for the substance to decay to 50% of its original amount. (b) To find the time it would take for the substance to decay to 5% of its original amount, we can use the same exponential decay formula.
(a) The half-life of a radioactive substance is the time it takes for the substance to decay to half of its original amount. In this case, the substance decayed to 95.5% of its original amount after one year. To find the half-life, we need to determine the time it takes for the substance to decay to 50% of its original amount. This can be calculated by using the exponential decay formula and solving for time.
(b) To find the time it would take for the substance to decay to 5% of its original amount, we can use the same exponential decay formula and solve for time. We substitute the decay factor of 0.05 (5%) and solve for time, which will give us the duration required for the substance to reach 5% of its original amount.
By calculating the appropriate time values using the exponential decay formula, we can determine both the half-life of the substance and the time it would take for the sample to decay to 5% of its original amount.
Learn more about exponential decay formula here:
https://brainly.com/question/28566787
#SPJ11
5x -3 (3x - 3 + 2x) >2( 3x - 20 + 4x)
Answers
Here is ur answer
- BRAINLIEST answerer


5x -3 (3x - 3 + 2x) >2( 3x - 20 + 4x)5x -3 (3x - 3 + 2x) >2( 3x - 20 + 4x)know i need points
Step-by-step explanation:
hi
Simplify the expression:
3p+–p
Answers
Answer:
3p-p
Step-by-step explanation:
I always think of the negative sign out ruling the positive sign so let's do that for the -p part.
3p-p is what it becomes
Your question says simplify but just in case you want the answer here it is:
-p is also the same as -1p
So therefore we have
3p-1p
And we subtract the coefficients and keep the variable
2p would be your answer but once again I don't know if you wanted that so just to be sure I put 3p-p as my "answer".
Molly was curious if quadrilateral A, B, C, D and E, F, G, H were congruent, so she tried to map one figure onto the other using transformations.


Answers
Answer: Choice C. No error. Molly is correct
Note how BC is 4 units high while FG is 5 units high. We don't have a match. So there is no way the figures are the same regardless of rigid transformations.
Answer:
Its c
Step-by-step explanation:
I got it right on khan academy
A computer was on sale for 270 if the original price was cut by 40% what was the original price
explain.
Answers
Answer: 108
Step-by-step explanation: The 40% percent taken away from $270 would be $108, because I round it to 50% percent off and that would $135 but since it's 40% off not 50% so I took away 10% from $135, and that's how I found my answer .
Which assertion relating to sales is most directly addressed when the auditors compare a sample of shipping documents to related sales invoices
Answers
When auditors compare a sample of shipping documents to related sales invoices, they are most directly addressing the assertion of accuracy of sales transactions.
What assertion do auditors address by comparing a sample of shipping documents to related sales invoices?Accuracy assertion refers to the correctness of the amounts and other details in the financial statements.
The shipping documents and sales invoices are important documents that provide evidence of sales transactions. The comparison of these documents helps to ensure that the sales invoices accurately reflect the goods shipped and the prices charged.
By comparing a sample of shipping documents to related sales invoices, auditors can verify that the sales recorded in the financial statements are accurate and complete.
Any discrepancies between the shipping documents and sales invoices can be investigated and resolved, which helps to ensure the accuracy of the sales transactions recorded in the financial statements. Therefore, the accuracy assertion is most directly addressed by this comparison.
Cutoff assertion refers to the timing of transactions recorded in the financial statements.
By comparing shipping documents to sales invoices, auditors can verify that sales have been recorded in the correct accounting period. Any shipping documents that relate to sales that occurred in a different period than the sales invoice can be investigated and corrected if necessary, which helps to ensure the accuracy of the sales transactions recorded in the financial statements.
Overall, comparing shipping documents to related sales invoices is an important procedure that helps auditors gather evidence to support the accuracy, completeness, and cutoff assertions related to sales transactions in the financial statements.
Learn more about Assertion
brainly.com/question/31568667
#SPJ11
Complete the explanation of how you can use equations with variables on both sides to solve real-world problems. (PLEASE HELP I GOT SCAMMED SEVERAL TIMES D:)
You can (blank) the costs of service that charge hourly or weekly rates.
A. Separate
B. Match
C. Compare
Answers
You can "compare" the costs of services that charge hourly or weekly rates using equations with variables on both sides.
Equations with variables on both sides can be used to solve real-world problems, such as comparing the costs of services that charge hourly or weekly rates.
For example, if a car rental company charges a weekly rate of $200 plus $0.25 per mile and another company charges a weekly rate of $150 plus $0.30 per mile, you can use equations with variables on both sides to determine which company offers the better deal based on the number of miles driven.
Let x be the number of miles driven and y be the total cost, then we can write two equations for the two companies:
Company A: y = 0.25x + 200
Company B: y = 0.30x + 150
We can then solve for x by setting the two equations equal to each other:
0.25x + 200 = 0.30x + 150
0.05x = 50
x = 1000
So if the number of miles driven is less than 1000, Company A is the better deal; if it's more than 1000, Company B is the better deal. Equations with variables on both sides can be used in various real-world situations to compare costs, determine rates, and solve other practical problems.
For more questions like Company click the link below:
https://brainly.com/question/30532251
#SPJ11
he vertices of a rectangle are plotted.
A graph with both the x and y axes starting at negative 8, with tick marks every one unit up to 8. The points negative 5 comma 2, 4 comma 2, negative 5 comma negative 4, and 4 comma negative 4 are each labeled.
What is the area of the rectangle?
15 square units
30 square units
45 square units
54 square units
Answers
Therefore, the area of the rectangle is 54 square units.
What must m∠QPS be for PQRS to be a parallelogram?
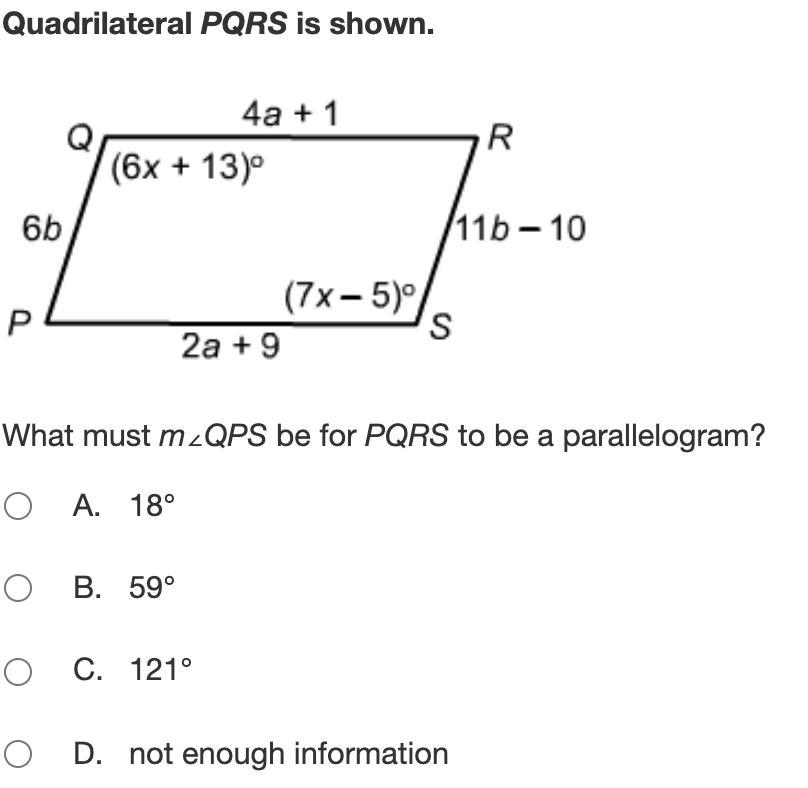
Answers
Answer:
18
Step-by-step explanation:
Alex’s times for running a mile are Normally distributed with a mean time of 5.28 minutes and a standard deviation of 0.38 seconds. Chris’s times for running a mile are Normally distributed with a mean time of 5.45 seconds and a standard deviation of 0.2 seconds. Ten of Alex’s times and 15 of Chris’s times are randomly selected. Let x Overbar Subscript Upper A Baseline minus x Overbar Subscript Upper C represent the difference in the mean times for Alex and Chris. Which of the following represents the standard deviation of the sampling distribution for x Overbar Subscript Upper A Baseline minus x Overbar Subscript Upper C?
0.09
0.13
0.17
0.18
Answers
The sampling distribution for x Overbar Subscript Upper A Baseline minus x Overbar Subscript Upper C is 0.13.
What is formula of standard deviation?The standard deviation of the sampling distribution for the difference in sample means can be calculated using the formula:
Standard deviation of the sampling distribution = √[(σ\(A^2\)/nA) + (σ\(C^2\)/nC)]
Where nA and nC are the sample sizes for Alex and Chris, respectively, and A and C are the standard deviations of the population for Alex and Chris, respectively.
Substituting the given values, we get:
Standard deviation of the sampling distribution = \(\sqrt{[(0.38^2/10) + (0.2^2/15)]}\)
= \(\sqrt{0.01444 + 0.00222}\)
= \(\sqrt{0.01666}\)
= 0.129
Therefore, the answer is 0.13.
know more about standard deviation visit :
https://brainly.com/question/23907081
#SPJ1
What is the answer to this equation (5+12i)+(7-5i)
Answers
The answer to the equation (5+12i) + (7-5i) is found to be 12-7i.
The provided equation is a simple algebraic relation between two complex numbers.
The given complex numbers are 5+12i and 7-5i.
We have to add these two complex numbers.
We will add the real part of the complex number to the real part and complex part of one complex number to the complex part of the complex number.
Sum of number = (5+12i) + (7-5i)
Sum of number = 12-7i
The sum of the two complex numbers is also complex number that has a real part has 12 and the imaginary or the complex part as -7.
To know more about Complex number, visit,
https://brainly.com/question/10662770
#SPJ4
Find the zeros and the axis of symmetry of the parabola.
a. zeros: 3, 5; x = 4
b. zeros: 3, 5; x = 8
c. zeros: 2, 4; x = 6
d. zeros: 2, 4; x = 3

Answers
Answer:
ok i think its D
Step-by-step explanation:
2,4; x= 3
i am not 100% but like i looked up examples and that seems to be the only one that looks right
Answer:
d. zeros: 2, 4 axis of symmetry: x = 3
Step-by-step explanation:
The zeros are the values of x where the graph crosses the x-axis
zeros = 2, 4
The axis of symmetry is the vertical line thru the vertex of the parabola
The vertex is (3, -1), so x = 3 is the axis of symmetry
Arrange from shortest to longest time:
3.44 ns
7.48 x 10^2 ps
1.55 x 10^-3 ms
Answers
To arrange the given times from shortest to longest, let's convert all the times to a common unit for easier comparison. Let's convert all the times to seconds (s). The correct arrangement from shortest to longest time is: 7.48 x \(10^{-4}\)µs, 3.44 x \(10^{-3}\) µs, 1.55 µs
1 ns = 10^-9 s (nanoseconds to seconds)
1 ps = 10^-12 s (picoseconds to seconds)
1 ms = 10^-3 s (milliseconds to seconds)
3.44 ns = 3.44 x 10^-9 s
7.48 x 10^2 ps = 7.48 x 10^-10 s
1.55 x 10^-3 ms = 1.55 x 10^-6 s
Arranging the times from shortest to longest:
7.48 x 10^-10 s (ps)
3.44 x 10^-9 s (ns)
1.55 x 10^-6 s (ms)
Therefore, the arranged times from shortest to longest are:
7.48 x 10^-10 s (ps) < 3.44 x 10^-9 s (ns) < 1.55 x 10^-6 s (ms)
Learn more about shortest to longest here:
brainly.com/question/32044710
#SPJ11
y = x sq+ 10 ; x = 3 find the value of the function rule
Answers
The value of the function is, y = 3.61
What is the value of the function?
The objective function's value at a solution is given by the value function of an optimization problem, which only depends on the problem's parameters.
Consider the given function,
\(y = \sqrt{x+10}\)
We have to find the value of y at x = 3.
So, plug x = 3 in the above equation.
We get,
\(y = \sqrt{3 + 10} = \sqrt{13} = 3.61\)
When we plug x = 3 then we get y = 3.61.
Therefore, the value of the given function is, y = 3.61
To know more about the Value of the function, click on the link
https://brainly.com/question/25638609
#SPJ1