The degree of precision of a quadrature formula whose error term is 27" (T) is: 22 5 2 3
Answers
The degree of precision of a quadrature formula with an error term of 27" (T) is 2.
To understand why the degree of precision is 2, let's first define what the degree of precision means in the context of quadrature formulas. The degree of precision refers to the highest power of x up to which the formula can integrate exactly. In other words, if a quadrature formula has a degree of precision of 2, it means that the formula can integrate exactly all polynomials of degree 2 or lower.
Now, to determine the degree of precision based on the given error term of 27" (T), we need to consider the approximation error. The error term T represents the maximum absolute difference between the exact integral and the approximate integral obtained using the quadrature formula.
In this case, the error term is given as 27" (T). The presence of the quotation mark (") indicates that the error term is measured in arc seconds. This suggests that the error is related to numerical integration over angles or circular arcs.
Since the error term is specified as 27" (T), we can conclude that the error is proportional to the square of the step size used in the quadrature formula. Therefore, the error term is of the order h^2, where h represents the step size.
Since the error term is of order h^2, it implies that the degree of precision is 2. This means that the quadrature formula can provide an exact result for polynomials of degree 2 or lower.
To know more about quadrature formulas , refer here:
https://brainly.com/question/31475940#
#SPJ11
Related Questions
Mr. McCoy's new ice cream shop is doing great! Last month, he sold out of his Boldly Buttered Popcorn ice cream and his Lovely Lavender Lemon ice cream. He sold x pints of Boldly Buttered Popcorn and y pints of Lovely Lavender Lemon. Each pint cost him $4 to make, and he charged $10 for each
Answers
After selling x pints of Boldly Buttered Popcorn icecream and y pints of Lovely Lavender Lemon on the charged of $10 for each, his profit equation is written as P = 6x + 6y = 6( x + y).
We have, Mr. McCoy's new ice cream shop. He sold two flavors of icecream. He sold his Boldly Buttered Popcorn ice cream and his Lovely Lavender Lemon ice cream. The quantity of sold Boldly Buttered Popcorn ice cream = x pints
The quantity of sold Lavender Lemon ice cream = y pints
Cost of each pint of ice cream = $4
Selling price of each pint of ice cream
= $10
First, total pints of icecream he sold
= pints of Boldly Buttered Popcorn ice cream+ pints of Lavender Lemon ice cream = ( x + y) pints
Now, Cost of (x + y) pints of ice cream
= $4 ( x + y)
Similarly, selling price of ( x + y ) pints of icecream = $ 10 ( x + y)
As we know, when selling price is greater than cost price then profit will occur. Equation for profit P = selling price - cost price = $ 10 ( x + y) - $4 ( x + y)
= 10 x + 10y - 4x - 4y
P = 6(x + y)
Hence, required equation is 6x + 6y.
For more information about equation, visit :
https://brainly.com/question/22688504
#SPJ4
Complete question:
Mr. McCoy's new ice cream shop is doing great! Last month, he sold out of his Boldly Buttered Popcorn ice cream and his Lovely Lavender Lemon ice cream. He sold x pints of Boldly Buttered Popcorn and y pints of Lovely Lavender Lemon. Each pint cost him $4 to make, and he charged $10 for each. Write an equation for his profit or loss on ice cream selling.
A vendor has $22.00 and wants to buy bushels of corn. The vendor finds a farmer who sells each bushel of corn for $3.00 and charges a fixed delivery fee of $5.50.
Answers
With $22.00 in hand, a $3.00 price per bushel, and a $5.50 delivery fee, the vendor can buy a maximum of 5 bushels of corn.
The vendor has $22.00.
The farmer sells each bushel of corn for $3.00.
The farmer also charges a fixed delivery fee of $5.50.
To determine how many bushels of corn the vendor can buy, we need to consider the cost of the corn itself and the delivery fee.
First, let's calculate how much money the vendor has left after deducting the delivery fee:
$22.00 (total money available) - $5.50 (delivery fee) = $16.50
Now, we know that the vendor has $16.50 remaining to spend on buying corn.
Next, we need to find out how many bushels of corn the vendor can purchase with the remaining amount. Since each bushel of corn costs $3.00, we divide the remaining money by the price per bushel:
$16.50 (remaining money) / $3.00 (price per bushel) = 5.5 bushels
However, we have a problem here. The vendor cannot buy a fraction of a bushel, as bushels are typically sold as whole units. Therefore, the vendor can only purchase a maximum of 5 bushels of corn.
In summary, with $22.00 in hand, a $3.00 price per bushel, and a $5.50 delivery fee, the vendor can buy a maximum of 5 bushels of corn.
Learn more about fraction here:
https://brainly.com/question/8482939
#SPJ11
Use standard Maclaurin Series to find the series expansion of f(x)=3e¹ ln(1 +82). a) Enter the value of the second non-zero coefficient: b) The series will converge if-d
Answers
a) The coefficient of x² in the given series expansion is [ln(83)]²/2!
b) The limit is less than 1, the series converges. The given series converges for all x.
The solution of the given problem is as follows:
a) Using standard Maclaurin series to find the series expansion of
f(x)=3e^(ln(1+82))
We have,
f(x)=3e^(ln(1+x))
Let
y=ln(1+x)
Then, x=e^(y)-1
So, f(x)=3e^(y)
Now, we can expand this function using standard Maclaurin Series which is given by
e^x=1 + x + x^2/2! + x^3/3! + …...
Therefore,
f(x)=3e^(y)=3[1 + y + y^2/2! + y^3/3! + …]
Now, substituting
y=ln(1+x) in the above series, we get
f(x)=3[1 + ln(1+x) + [ln(1+x)]^2/2! + [ln(1+x)]^3/3! + …]
The value of the second non-zero coefficient is as follows:
The second non-zero coefficient is the coefficient of x² in the given series expansion.Therefore, the coefficient of x² in the given series expansion is [ln(83)]²/2!
which is the value of the second non-zero coefficient.
b) The series will converge if-d
Let us first consider the radius of convergence of the series. Since the given function is analytic at x=0, the Maclaurin Series will converge within a radius of convergence.
So, we need to find the radius of convergence of the series.
To find the radius of convergence, we can use the ratio test which is given by:
|a_(n+1)/a_n|
= lim_(x→∞) (a_(n+1)/a_n)
Where, a_n is the nth term of the series expansion and
n=0, 1, 2, 3, ……
Here,
a_n = [ln(83)]^n/n!
So,
|a_(n+1)/a_n|
= |[ln(83)]^(n+1)/(n+1)!|/|[ln(83)]^n/n!|
taking limit n→∞,
we get
|a_(n+1)/a_n| = lim_(x→∞) |[ln(83)]^(n+1)/(n+1)!|/|[ln(83)]^n/n!|
= lim_(x→∞) [ln(83)/(n+1)] = 0
Thus, since the limit is less than 1, the series converges. The given series converges for all x.
To know more about series converges visit:
https://brainly.com/question/32549533
#SPJ11
3x^2-9x+2 in standard form
Answers
The standard form of 3x² - 9x + 2 is 3x² - 9x + 2.
What is a quadratic function?A polynomial function with one or more variables, where the largest exponent of the variable is two, is referred to as a quadratic function. In other terms, a "polynomial function of degree 2" is a quadratic function.
Given:
A quadratic function,
3x² - 9x + 2.
The standard form of the quadratic function is
ax² + bx + c.
The standard form of 3x² - 9x + 2 is 3x² - 9x + 2.
Therefore, 3x² - 9x + 2.
To learn more about the quadratic function;
https://brainly.com/question/11485644
#SPJ1
en el diagrama de venn donde van ubicados estos numeros?
0,88888....
1 sobre 7 pi
-6 sobre 3
4E
55 sobre 0
56 sobre 9
-0,65999999
Answers
Answer:
Step-by-step explanation:
a local travel office has 10 employees. their monthly salaries are given below. find the mean. 1550, 1710, 1630, 1000, 1400, 1610, 1890, 1300, 2700, 5800
Answers
The mean is a measure of central tendency that represents the average value of a set of data. To find the mean of the monthly salaries of the 10 employees in the local travel office, we need to add up all the salaries and divide by the total number of employees.
So, if we add up all the salaries, we get:
1550 + 1710 + 1630 + 1000 + 1400 + 1610 + 1890 + 1300 + 2700 + 5800 = 19,940
Then, we divide this sum by the total number of employees, which is 10.
Mean = 19,940 / 10 = 1,994
Therefore, the mean monthly salary for the 10 employees in the local travel office is $1,994.
It's important to note that the mean is a useful measure of central tendency, but it can be affected by outliers. In this case, the salary of $5,800 is significantly higher than the other salaries, which may skew the mean. To get a better understanding of the distribution of salaries, it may be useful to also look at other measures such as the median and mode.
To find the mean monthly salary of the 10 employees at the local travel office, follow these steps:
1. Add up all the monthly salaries: 1550 + 1710 + 1630 + 1000 + 1400 + 1610 + 1890 + 1300 + 2700 + 5800 = 20,590.
2. Divide the total sum by the number of employees (10): 20,590 / 10 = 2,059.
The mean monthly salary of the 10 employees at the local travel office is 2,059. The mean represents the average salary of the employees, providing a general idea of the salary level at the office. In this case, the mean gives a local perspective on the financial situation of the employees within the travel office, allowing for comparisons with other companies or the industry standard.
More on Mean: https://brainly.com/question/1136789
#SPJ11
Patrick collects baseball cards. He currently has 30 cards, and buys 4 new cards a week. How many cards will Patrick have in 12 weeks.
Answers
Answer:
The answer would be 78
Step-by-step explanation:
4 x 12 = 48
48 + 30 = 78
Therefore the answer is 78
(Why? Use this equation: 30(12 x 4). After using order of operations, you will get 78.)
this pentagonal right pyramid has a base area of 30 m 2 30 m 2 30, start text, space, m, end text, squared. a pentagonal right pyramid with a triangular face height of seven meters, a triangular face side of eight meters, and the pyramid's vertical height of five meters. what is the volume of the figure? m 3 m 3
Answers
The z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
The z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
How to find the Z score
P(Z ≤ z) = 0.60
We can use a standard normal distribution table or a calculator to find that the z-score corresponding to a cumulative probability of 0.60 is approximately 0.25.
Therefore, the z-score for P(? ≤ z ≤ ?) = 0.60 is approximately 0.25.
For the second question:
We want to find the z-score such that the area under the standard normal distribution curve to the right of z is 0.30. In other words:
P(Z ≥ z) = 0.30
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to a cumulative probability of 0.30 is approximately -0.52 (since we want the area to the right of z, we take the negative of the z-score).
Therefore, the z-score for P(z ≥ ?) = 0.30 is approximately -0.52.
Read more on Z score here: brainly.com/question/25638875
#SPJ1
Which of the following statements about a least-squares regression analysis is true?
a. If the least squares regression line of yon xis y = 4 + 2x, then the least squares regression line of xon y is x=-2 +0.5y. b. The percentage of variation in y explained by x (or by the regression model y on x) is the same as the percentage of variation in x explained by y (or by the regression model of xony). c. There is no unit measurement for the slope of the regression line. d. The y-intercept and slope of the regression line have the same unit measurement. e. Correlation and slope of the regression line have the same unit measurement.
Answers
The correct statement about a least-squares regression analysis is: The y-intercept and slope of the regression line have the same unit measurement. The correct option is d.
a. This statement is false. If the least squares regression line of y on x is y = 4 + 2x, the least squares regression line of x on y would be x = -2 + 0.5y.
b. This statement is false. The percentage of variation in y explained by x is not necessarily the same as the percentage of variation in x explained by y. The correlation coefficient measures the strength and direction of the linear relationship between two variables.
c. This statement is false. The slope of the regression line does have a unit measurement. It represents the change in the dependent variable (y) for a one-unit change in the independent variable (x).
d. This statement is true. The y-intercept and slope of the regression line have the same unit measurement. The y-intercept represents the value of the dependent variable (y) when the independent variable (x) is zero, and the slope represents the change in y for a one-unit change in x.
e. This statement is false. Correlation and slope of the regression line do not have the same unit measurement. The correlation coefficient is a dimensionless measure that ranges from -1 to 1, indicating the strength and direction of the linear relationship between two variables. The slope of the regression line has a unit measurement based on the units of the dependent and independent variables. The correct option is d.
To know more about least-squares regression analysis, refer here:
https://brainly.com/question/28298210#
#SPJ11
Jorge wants to order tickets online so that he and 4 of his friends can go together to a movie. The cost of the tickets is $12.00 per person. The website also charges a transaction fee of $2.75 for the tickets online. Write an expression in terms of m that represents the cost of ordering m tickets online.Jorge wants to order tickets online so that he and 4 of his friends can go together to a movie. The cost of the tickets is $12.00 per person. The website also charges a transaction fee of $2.75 for the tickets online. Write an expression in terms of m that represents the cost of ordering m tickets online.
Answers
Answer:
if m stands for number of tickets
then amount would be
12+2.75*m
14.75m
Step-by-step explanation:
chegg a 12 ft ladder is leaning against a wall. if the top of the ladder slides down the wall at a rate of 4 ft/s, how fast (in ft/s) is the bottom moving along the ground when the bottom of the ladder is 6 ft from the wall?
Answers
The bottom is moving at a rate of \(4\sqrt{3}\) ft/s along the ground when the botton of the ladder is at a distance of 6 ft from the wall.
Here we have been mentioned that a 12 feet ladder is leaning against the wall which is represened by AC in the below given triangle.
We have AB = y = distance of top of the ladder from the wall
BC = x = distance of bottom of the ladder from the wall
AC = z = height of the ladder = 12 ft (given)
The top of the ladder AB is sliding down at a rate of 4 \(ft/s\)
∴ \(\frac{dy}{dt}\) = - 4 ft/s (negative sign indicates that the top is sliding downwards)
Let the rate at which the bottom of the ladder is sliding be \(\frac{dx}{dt}\)
Now in the right angled triangle \(ABC\) by using Pythagoras theorem we have,
\(AB^{2} + BC^{2} =\)\(AC^{2}\)
\(y^{2} +x^{2} = z^{2}\) (equation 1)
When x = 6ft and z = 12 ft,
\(y^{2} +6^{2} = 12^{2}\)
⇒ \(y^{2} = 144 - 36\)
⇒ \(y^{2} = 108\)
⇒ y = √108
⇒ y = 6 √3 ft
Differentiating equation 1 with respect to \(time\) we get,
\(\frac{d}{dt} (y^{2} +x^{2} ) = \frac{d}{dt} (z^{2})\)
⇒ 2y\(\frac{dy}{dt}\) + 2x\(\frac{dx}{dt}\) = 2z\(\frac{dz}{dt}\)
Putting the values of dz/dt = 0 (as the height is constant) , dy/dt = - 4 ft/s , y = 6 √3 ft, x = 6ft and z = 12ft we have,
∴ 2(6√3) (-4) + 2(6)\(\frac{dx}{dt}\) = 2(12)(0)
⇒ -48√3 + 12\(\frac{dx}{dt}\) = 0
⇒ 12\(\frac{dx}{dt}\) = 48√3
⇒ \(\frac{dx}{dt} = \frac{48\sqrt{3} }{12}\)
⇒ \(\frac{dx}{dt} = 4\sqrt{3}\) ft/s
Hence the rate at which the bottom of the ladder is sliding is \(\frac{dx}{dt} = 4\sqrt{3}\) ft\s
To know more about rate click here:
https://brainly.com/question/25146836
#SPJ4

13. A class has 10 students of which 4 are male and 6 are female. If 3 students are chosen at random from the class, find the probability of selecting 2 females using binomial approximation. a) 0.288 b) 0.720 c) 0.432 d) 0.240
Answers
C. 0.432 is the probability of selecting 2 females using binomial approximation.
The given problem can be solved by using the binomial distribution formula, which is given by:
p(x) = C(n, x) * p^x * q^(n-x)
Where:
p(x) = probability of x successes in n trials
C(n, x) = combination of n things taken x at a time
p = probability of success
q = probability of failure
q = 1 – p
In this case, the probability of selecting 2 females is to be determined. Therefore, x = 2.
Let us substitute the given values in the formula:
p(x = 2) = C(n, x) * p^x * q^(n-x) = C(3, 2) * (6/10)^2 * (4/10)^1 = 0.432
Therefore, the probability of selecting 2 females using binomial approximation is 0.432, which is option c.
To learn more about probability, refer below:
https://brainly.com/question/31828911
#SPJ11
Colleen is attending a carnival. The price of admission to the carnival is shown. It costs $3 to play a game. Colleen has $35.
A Ferris wheel is shown. Carnival admission is eight dollars.
What is the greatest number of games she can play?
Answers
Answer:
9
Step-by-step explanation:
Reduce the admission fee. Then divide the rest with cost per game
35 - 8 = 27
=> 27/3 = 9
. let u = <4,8>, v = <-2, 6>. find u + v. (1 point)
how to find find u+v?
Answers
The sum of vectors u = <4,8>,and v = <-2, 6> i.e. (u+v) is <2, 14>
To find the sum of vectors u and v (u+v), you need to perform the following steps:
1. Identify the components of vectors u and v: u = <4, 8> and v = <-2, 6>.
2. Add the corresponding components of both vectors: To find the sum (u+v), add the x-components (4 and -2) and the y-components (8 and 6) separately.
3. Calculate the sum of the x-components: 4 + (-2) = 2.
4. Calculate the sum of the y-components: 8 + 6 = 14.
5. Combine the results to form the new vector (u+v): <2, 14>.
So, the sum of vectors u and v (u+v) is <2, 14>.
To know more about vectors refer here:
https://brainly.com/question/13322477#
#SPJ11
Describe how to compare the two ratios 5:8 to 7:9. Tell each step to set up the ratios, then explain what to do to be able to compare the ratios. Finally make sure to answer how the ratios compare. ~ 100 POINTS AND ILL GIVE YOU BRAINLIEST IF YOU ANSWER CORRECTLY AND 5 SENTENCES NEEDED
Answers
Answer:
5/8 is smaller.
Step-by-step explanation:
A ratio is just a different type of fraction, a 5:8 ratio means 5/8 which is 0.625. A 7:9 ratio equals 7/9 which is 0.777777
Then to compare them you see which is smaller or bigger.
0.77777 is bigger than 0.625 so we know that 0.77777777 which was the 7:9 ratio is the bigger one.
Steps:-
First rewriteThen convert to fractionsThen divide both\(\\ \rm\rightarrowtail 5:8::7;9\)
\(\\ \rm\rightarrowtail 5/8:7/9\)
\(\\ \rm\rightarrowtail \dfrac{5(9)}{8(9)}:\dfrac{7(8)}{9(8)}\)
\(\\ \rm\rightarrowtail \dfrac{45}{72}:\dfrac{56}{72}\)
\(\\ \rm\rightarrowtail \dfrac{45}{56}\)
Second one is biggerHelp me please with this problem

Answers
Step-by-step explanation:
Area of a rhombus = ab/2 where a is 12cm and b is 10cm (diagonals)
Area = 12 x 10 /2 =120/2
Area = 60cm
the pitcher's mound in softball is 40 feet from home plate if it takes 5.4 second for the pitch to reach home plate how fast is the pitch
PLZ HELP
Answers
Answer:
7.4/feetStep-by-step explanation:
40 : 5.4 = 7.4
#Let'sLearn

Helpppppppppo meeeee plsssss

Answers
Answer:
Step-by-step explanation:
\(38.7=\) \(38.7 / 10^{2}\)
\(38.7= 38.7 times 10^{3}\)
\(38.7=38.7 times 10^{4}\)
Hope this helps :)
PLZ HELP DUE IN AN HOUR plz do number 9

Answers
Answer:
part one: her pay is raised by 0.91 per hour
part 2: $325 before raise; $347.75 after raise
Step-by-step explanation:
How to solve this Q?

Answers
Answer:
\( \frac{61}{20} \)
Step-by-step explanation:
\( \frac{3}{4} + ( \frac{4}{3} - \frac{1}{2} + \frac{2}{3} + \frac{4}{5} ) \\ \\ \frac{3}{4} + (( \frac{4}{3} - \frac{1}{2}) - \frac{2}{3} + \frac{4}{5} ) \\ \\ \frac{3}{4} + ( \frac{4 + 3}{3} - \frac{1}{2} + \frac{4}{5} \\ \\ \frac{3}{4} + ( \frac{6}{3} - \frac{1}{2} + \frac{4}{5}) \\ \\ \frac{3}{4} + (2 - \frac{1}{2} + \frac{4}{5} )\\ \\ \frac{3}{4} + \frac{20 - 5 + 8}{10} \\ \\ \frac{3}{4} + \frac{15 + 8}{10} \\ \\ \frac{3}{4} + \frac{23}{10} \\ \\ \frac{15 + 46}{20} \\ \\ \frac{61}{20} \)
in each of problems 38 through 42, a differential equation and one solution y1 are given. use the method of reduction of order as in problem 37 to find a second linearly independent solution y2.38. x2y′′+xy′−9y=0(x>0);y1 (x)=x339. 4y′′−4y′+y=0;y1 (x)=ex/2 40. x2y′′−x(x+2)y′+(x+2)y=0(x>0);y1 (x)=x41. (x+1)y′′−(x+2)y′+y=0(x>−1);y1 (x)=ex42. (1−x2)y′′+2xy′−2y=0(−1
Answers
By using the method of reduction of order as in differential equation to find a second linearly independent solution of the: Equation x2y" + xy' – 9y = 0 (x > 0); yı(x) = x3 has general solution is y(x) = c1x^3 + c2x^(-2),
Equation 4y" – 4y' + y = 0; yı(x) = ex/2 general solution is y(x) = c1exp(x/2) + c2*exp(-x/2),
Equation x2y" – x(x + 2)y' + (x + 2)y = 0 (x > 0); yı(x) = x has general solution y2(x) = (C3x^(3/2) + C4)e^(-x).
Equation (x + 1)y" - (x + 2)y' + y = 0 (x > -1); yı(x) = ex has the general solution y(x) = c1ex + [c2 - ln(|2x + 1|)/2]ex.
Using the method of reduction of order, assume a second solution of the form y2(x) = u(x)y1(x). Then we have:
y'1(x)u(x) + y1(x)u'(x) = 0
u'(x) = -y'1(x)u(x)/y1(x)
Integrating both sides:
ln|u(x)| = -ln|y1(x)| + C
u(x) = K/x^3
Plugging this into the differential equation:
x^2y'' + xy' - 9y = 0
x^2[u''(x)y1(x) + 2u'(x)y1'(x) + u(x)y1''(x)] + x[u'(x)y1(x) + u(x)y1'(x)] - 9u(x)y1(x) = 0
Simplifying and dividing by x^2y1(x):
u''(x) - 6/x^2 u(x) = 0
Equation r(r-1) - 6 = 0, which has roots r = 3 and r = -2. Therefore, the general solution is y(x) = c1x^3 + c2x^(-2).
Using the method of reduction of order, assume a second solution of the form y2(x) = u(x)y1(x). Then we have:
y'1(x)u(x) + y1(x)u'(x) = 0
u'(x) = -y'1(x)u(x)/y1(x)
Integrating both sides:
ln|u(x)| = -2ln|y1(x)| + C
u(x) = Kexp(-x/2)
Plugging this into the differential equation:
4y'' - 4y' + y = 0
4[u''(x)y1(x) + 2u'(x)y1'(x) + u(x)y1''(x)] - 4[u'(x)y1(x) + u(x)y1'(x)] + u(x)y1(x) = 0
Simplifying and dividing by 4y1(x):
u''(x) - u(x)/4 = 0
equation r^2 - 1/4 = 0, has roots r = 1/2 and r = -1/2. Therefore, the general solution is y(x) = c1exp(x/2) + c2*exp(-x/2).
Let y2(x) = v(x)y1(x), where v(x) is a function to be determined.
Then, y'2(x) = v'(x)y1(x) + v(x)y'1(x) and y"2(x) = v"(x)y1(x) + 2v'(x)y'1(x) + v(x)y"1(x).
Substituting y1(x) and y2(x) into the given differential equation, we get:
x^2(v"(x)y1(x) + 2v'(x)y'1(x) + v(x)y"1(x)) - x(x+2)(v'(x)y1(x) + v(x)y'1(x)) + (x+2)v(x)y1(x) = 0
Simplifying and dividing by x^2y1(x), we obtain:
v"(x) + (2/x - (x+2)/x^2)v'(x) + ((x+2)/x^2 - 1/x^2)v(x) = 0
Let u(x) = v'(x). Then, the above equation can be written as a first-order linear differential equation:
u'(x) + (2/x - (x+2)/x^2)u(x) + ((x+2)/x^2 - 1/x^2)v(x) = 0
Using an integrating factor of exp(∫[(2/x - (x+2)/x^2)dx]), we get:
u(x)/x^2 = C1 + C2∫exp(-2lnx)exp((x+2)/x)dx
u(x)/x^2 = C1 + C2/x^2e^(x+2)
v(x) = C3x^(1/2)e^(-x) + C4x^(-3/2)e^(-x)
Therefore, the second linearly independent solution is:
y2(x) = (C3x^(3/2) + C4)e^(-x)
41. (x + 1)y" - (x + 2)y' + y = 0, one solution y1(x) = ex.
We assume that the second solution has the form y2(x) = v(x)ex.
We can then find y2'(x) and y2''(x) as follows:
y2'(x) = v'(x)ex + v(x)ex
y2''(x) = v''(x)ex + 2v'(x)ex + v(x)ex
We can substitute y1(x) and y2(x) into the differential equation and simplify using the above expressions for y2'(x) and y2''(x):
(x + 1)[v''(x)ex + 2v'(x)ex + v(x)ex] - (x + 2)[v'(x)ex + v(x)ex] + v(x)ex = 0
Simplifying and dividing by ex, we get:
xv''(x) + (2x + 1)v'(x) = 0
This is a first-order linear differential equation, which we can solve using separation of variables:
v'(x) = -1/(2x + 1) dv/dx
Integrating both sides
v(x) = C1 - ln(|2x + 1|)/2
where C1 is a constant of integration.
Therefore, the second linearly independent solution is:
y2(x) = v(x)ex = [C1 - ln(|2x + 1|)/2]ex
So, the general solution is:
y(x) = c1ex + [c2 - ln(|2x + 1|)/2]ex
where c1 and c2 are constants of integration.
To know more about Differential equation;
https://brainly.com/question/28099315
#SPJ4
____The given question is incomplete, the complete question is given below:
In each of Problems 38 through 42, a differential equation and one solution yı are given. Use the method of reduction of or- der as in Problem 37 to find a second linearly independent solution y2. 38. x2y" + xy' – 9y = 0 (x > 0); yı(x) = x3 39. 4y" – 4y' + y = 0; yı(x) = ex/2 40. x2y" – x(x + 2)y' + (x + 2)y = 0 (x > 0); yı(x) = x 41. (x + 1)y" - (x + 2)y' + y = 0 (x > -1); yı(x) = ex
as the number of degrees of freedom become large, the t distribution approaches the binomial distribution. group of answer choices true false
Answers
As the number of degrees of freedom become large, the t distribution actually approaches the normal distribution, not
the binomial distribution. The correct answer is false.
The t distribution is used when the sample size is small and the population standard deviation is unknown, while the
binomial distribution is used for discrete data where there are only two possible outcomes.
The binomial distribution is a discrete probability distribution that models the number of successes in a fixed number of
independent trials with a constant probability of success, whereas the t distribution is a continuous probability
distribution that models the variability of sample means from a normal population.
for such more question on t distribution
https://brainly.com/question/24277447
#SPJ11
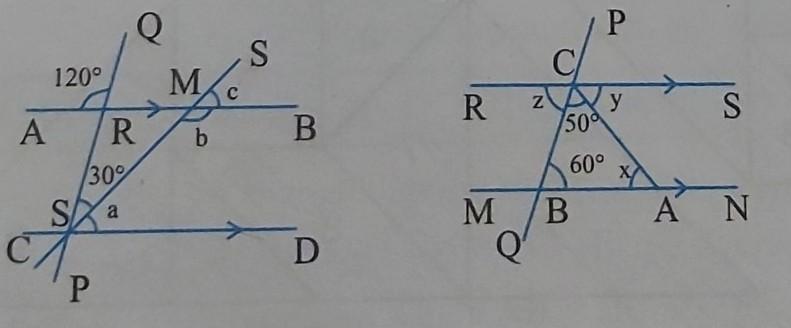
find the value of A , B and C from the following figure
Answers
Step-by-step explanation:
Question 1 :Here in the given figure b and 30° are alternate to each other so it can be name as alternative angle....
b = 30°
Now...
a + 30° = 180° ( being supplementary angle )
a = 180° - 30°
a = 150°
Now the value of c will be 150° being corresponding
angle with a
c = 150°
Question 2 :z = 60° ( being alternative angle )
Now let's find the value of x.....
here ,
60° + 50° + x = 180° ( the sum of interior angle of triangle is 180°
x = 180° - 110°
x = 70°
Now...
y = 70° ( alternative angle )
\(....\)
(it urgent)
Find the AREA of the SHADED REGION

Answers
Answer:
i will answer but there is no picture
Step-by-step explanation:
sorry
Find g(x), where g(x) is the translation 6 units left and 4 units up of f(x)=x2
Answers
The transformation of f(x) to g(x) is g(x) = (x + 6)² + 4
Describing the transformation of f(x) to g(x).From the question, we have the following parameters that can be used in our computation:
The functions f(x) and g(x)
Where, we have
f(x) = x²
The translation 6 units left and 4 units up means that
g(x) = f(x + 6) + 4
So, we have
g(x) = (x + 6)² + 4
This means that the transformation of f(x) to g(x) is g(x) = (x + 6)² + 4
Read more about transformation at
brainly.com/question/27224272
#SPJ1
− 2|5 − 1| − 3 =− 11 Pls help
The lines mean absolute value.
Answers
Not sure what the question is, but both sides are equal to each other. -11=-11, so if the question is if both sides are equal, then it's true
7. Refer to the bar chart in question 6. Which age group recorded the highest number of children

Answers
Answer:
The age group that recorded the highest number of children is 7.
Step-by-step explanation:
We can clearly can see from the graph, that the 7 year old age group has 5 children, which is more than the rest of the age groups.
Hope this helps:) Goodluck!
Any Gaokao Questions?
PLEASE I WANT ONE
Answers
Answer:
what is Gaokao birthday
Answer:
What motivating factors contribute to students preparing so hard for the gaokao test? What are they hoping to accomplish by passing it? What happens to those who don't pass?
Step-by-step explanation:
The speeds of the fastballs thrown by major league baseball pitchers were measured by radar gun. The mean speed was 87 miles per hour. The standard deviation of the speeds was 3 mph. Which of the following speeds would be classified as an outlier?
a. 84 mph b. 92 mph c. 97 mph d. 81 mph
Answers
Thus, the answer is option (c) 97 mph.
An outlier is a value that lies significantly away from the rest of the values in the dataset. For a given dataset, we can determine outliers using z-scores.According to the problem statement, the mean speed of the fastballs thrown by major league baseball pitchers is 87 mph, and the standard deviation is 3 mph. To determine which speed is an outlier, we need to find its corresponding z-score.z = (x - μ) / σHere, x is the speed we want to test, μ is the mean speed, and σ is the standard deviation of speeds.Using the formula above, we can calculate the z-scores for each speed given in the options:a. z = (84 - 87) / 3 = -1b. z = (92 - 87) / 3 = 1.67c. z = (97 - 87) / 3 = 3.33d. z = (81 - 87) / 3 = -2Since a z-score of ±2 or higher is generally considered an outlier, the speeds of 97 mph and 81 mph are classified as outliers. Thus, the answer is option (c) 97 mph.
To know more about speed,
https://brainly.com/question/13943409
#SPJ11
Explain why 2 is NOT a solution of x 7 5
Answers
Based on the information provided, 2 is not a solution of x>5 because a possible solution requires a number greater than 5.
How to solve inequality?Inequalities include symbols such as >, ≤, ≥, among others that should be interpreted correctly to solve the inequality. In this case, the symbol in the inequality is >, which means greater than. Based on this, the value of x should be greater than 5, for example, 7, 19, 2948, etc.
Therefore, 2 is not a solution to the inequality x>5 because a number greater than 5 rather than less than 5 is required to solve this expression.
Note: This question is incorrect and incomplete; here is the complete question:
Explain why 2 is NOT a solution of x>5
Learn more about inequalities in https://brainly.com/question/30231190
#SPJ1