The cost of 3 scarves is $72.75. What is the unit price?
Answers
Answer: $8.75
Step-by-step explanation:

Related Questions
Solve Laplace's equation inside a circular annulus (a < r < b) with the following boundary conditions;
(∂u/∂r)(a,θ) = f(θ),
(∂u/∂r)(b,θ) = g(θ)
Is there a solvability constraint on this problem? If so, what is it?
Answers
There is a solvability constraint on this problem which is B₀ = 0.Note: The function u(r,θ) is not uniquely defined if B₀ ≠ 0.
The Laplace's equation inside a circular annulus (a < r < b) with the following boundary conditions is given as;∂u/∂r (a,θ) = f(θ),∂u/∂r (b,θ) = g(θ)
The expression for Laplace's equation inside a circular annulus is given as;∂²u/∂r² + 1/r ∂u/∂r + 1/r² ∂²u/∂θ² = 0.
The general solution of the above Laplace's equation is given as;
u(r,θ) = (A₀ + B₀ ln(r)) + ∑ [Aₙ rⁿ + Bₙ r⁻ⁿ] (n = 1,2,3,....)×[Cₙ cos(nθ) + Dₙ sin(nθ)]where, A₀, B₀, Aₙ, Bₙ, Cₙ and Dₙ are constants.
The solvability constraint on this problem is the problem of uniqueness. The function u(r,θ) has a unique solution if the constant B₀ = 0 which is the solution of the Laplace's equation inside a circular annulus (a < r < b) with the following boundary conditions.
Therefore, there is a solvability constraint on this problem which is
B₀ = 0.
Note: The function u(r,θ) is not uniquely defined if B₀ ≠ 0.
To know more about: Laplace's equation
https://brainly.com/question/31583797
#SPJ11
you need to add lines, segments, and angles to create your ultimate circle. you need to incorporate specific theorems. Each problem must ask for a missing measure(an arc measure, segment length or angle measure. Provide information that someone would need to solve at the top of the puzzle could include angle measures, arc measures, tangent lines, parallel ect. You must list which problem number is used for each listed theorem show all work.

Answers
Some information that someone might use to solve problems related to a circle design is the Tangent Arc theorem.
What is the tangent arc theorem?The tangent arc theorem states that if an angle is formed by two secants, one secant, one tangent, or two tangents, and also intersects in a space outside of the circle, then the value obtained will be equal to the difference of the values of the intercepted arcs divided by one and a half.
Also, note that angles outside a circle are those whose vertex or arc is pointed outwards and their sides are either secants or tangents. With this information, it will be possible to solve problems related to tangent lines and arc measures.
Learn more about the tangent arc theorem here:
https://brainly.com/question/29239907
#SPJ1
2x + 3 = 23 steps for x?
Answers
Answer:
x=10
Step-by-step explanation:
work in the photo

Answer:
x=10
Step-by-step explanation:
Subtract 3 from both sides
2x=23-3
Simplify 23-3 to 20
2x=20
Divide both sides by 2
x= 2 0/2
Simplify 20/2 to 10
x=10
I need help like asap !!!
only numbers and decimal points

Answers
Answer:
a = 4.52 km
Step-by-step explanation:
Formula we use,
→ (AC)² = (BC)² + (AB)²
Now the value of a will be,
→ (7.2)² = a² + (5.6)²
→ 51.84 = a² + 31.36
→ a² = 51.84 - 31.36
→ a = √20.48
→ [ a = 4.52 km ]
Hence, value of a is 4.52 km.
Mary and Bill both are saving money. Mary already has $30 and is able to save $5.50 every week. Bill already has $45 and is able to save $4.25 every week. When will Mary and Bill have the same amount of money?
Answers
Answer: 12 weeks
Step-by-step explanation:
Let the week that both of them will have thesame amount of money be represented by x.
Since Mary already has $30 and is able to save $5.50 every week, this will be denoted as: 30 + 5.50x
Since Bill already has $45 and is able to save $4.25 every week, this will be debited by 45 + 4.25x. Then we'll equate both equations and this will be:
30 + 5.50x = 45 + 4.25x
5.50x - 4.25x = 45 - 30
1.25x = 15
x = 15/1.25
x = 12
They'll have thesame amount of money in 12 weeks.
At a local restaurant the amount of time that customers have to wait for their food is normally distributed with a mean of 42 minutes and a standard deviation of 2 minutes. using the empirical rule, what percentage of customers have to wait between 36 minutes and 48 minutes?
Answers
By using empirical rule, 99.7% of the customers have to wait between 36 minutes and 48 minutes.
To determine the percentage of customers who have to wait between 36 minutes and 48 minutes, we can use the empirical rule (also known as the 68-95-99.7 rule) for a normal distribution.
According to the empirical rule:
Approximately 68% of the data falls within one standard deviation of the mean.Approximately 95% of the data falls within two standard deviations of the mean.Approximately 99.7% of the data falls within three standard deviations of the mean.In this case, the mean is 42 minutes and the standard deviation is 2 minutes.
To find the percentage of customers who have to wait between 36 minutes and 48 minutes, we can calculate the z-scores for these values and then determine the percentage of data within that range.
The z-score is calculated using the formula:
z = (x - mean) / standard deviation
For 36 minutes:
z₁ = (36 - 42) / 2 = -3
For 48 minutes:
z₂ = (48 - 42) / 2 = 3
Since the z-scores fall within the range of -3 to 3, which is within three standard deviations of the mean, we can conclude that approximately 99.7% of the customers will have to wait between 36 minutes and 48 minutes.
To learn more about standard deviation:
https://brainly.com/question/475676
#SPJ11
Answer:
95%
Step-by-step explanation:
W Answer
if you roll a two fair 6 sided dice the sum is 4 and higher
Answers
The probability that the sum is 4 or higher is 11/12.
What is the probability?Probability in mathematics is the possibility of an event in time. In simple words, how many times does that incident is happening in any given time interval.
Given:
You rolled two fair 6 sided dice.
The total number of outcomes = 6 x 6 = 36.
The sample space that does not satisfy the condition,
S = {1 + 1, 1 + 2, 2 + 1}
The possible outcomes = 36 - 3 = 33
The probability that the sum is 4 or higher,
= 33/36
= 11/12
Therefore, 11/12 is the probability.
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
7. IfQ, and Q2 are orthogonal 1 X matrices, show that the product QO2 is orthogonal.
Answers
The product of the two matrices Q₁Q₂ is orthogonal
What i orthogonal matrix?In linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal vectors. ... {\displaystyle Q^{\mathrm {T} }Q=QQ^{\mathrm {T} }=I,} where QT is the transpose of Q and I is the identity matrix.
It is said to be an orthogonal matrix if its transpose is equal to its inverse matrix, or when the product of a square matrix and its transpose gives an identity matrix of the same order.
If A is an n*n orthogonal matric, then A*A¹ = A¹*A
Therefore A*A¹ = A¹*A = 1
This implies that the product Q₁O₂ is orthogonal.
Learn more about orthogonal matrix on https://brainly.com/question/31053015
#SPJ4
Round $\frac{100}{111}$ to the nearest thousandth.
Answers
The value of the expression 100 ÷ 111 nearest to the thousandth will be 0.901.
What is Algebra?Algebra is the study of algebraic expressions, while logic is the manipulation of those concepts.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This rule is used to answer the problem correctly and precisely.
The numbers are given below.
100 and 111
Then the division of the numbers 100 and 111 will be given by putting a division sign between them. Then we have
⇒ 100 ÷ 111
⇒ 100 / 111
⇒ 0.900900900
⇒ 0.901
The worth of the articulation 100 ÷ 111 closest to the thousandth will be 0.901.
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
A small corporation borrowed $500,000 to expand its software line with
an interest $43,500. Some of the money was borrowed at 8%, some at
9%, and some at 10%. The amount borrowed at 8% was two and half
times the amount borrowed at 10%. How much did the corporation invest
at 9% interest? (Write only the amount.)
Answers
Answer:
i have no ideo
Step-by-step explanation:
The population for Rainbow City is 36,000. The growth rate is 3%. About how many people will it have after 5 years
Answers
Answer:
41,500 people
Step-by-step explanation:
First you find 3% of 36,000= 1,080
Then you do 1080 x 5= 4,500
Then finally do 36,000 + 4,500= 41,500
How many players had a single rate of greater than 0.2 per plate appearance over 1999-2001?
Answers
The exact number of players meeting your criteria will depend on the specific database you use and the parameters you set for the search.
To determine the number of players who had a single rate greater than 0.2 per plate appearance over the period from 1999 to 2001, we would need access to a comprehensive database of baseball statistics for that time frame. Unfortunately, as an AI language model, my knowledge cutoff is in September 2021, and I don't have real-time access to current or future sports statistics.
However, I can guide you on how to obtain the information you're looking for. You can consult baseball reference websites, such as Baseball-Reference.com or Fangraphs.com, which provide detailed player statistics for different seasons and allow you to filter data based on specific criteria.
Using these websites, you can search for players who played in Major League Baseball from 1999 to 2001 and examine their individual statistics, including their single rate (number of singles divided by plate appearances). By applying a filter for a single rate greater than 0.2, you can determine the number of players who meet that criteria.
Keep in mind that the exact number of players meeting your criteria will depend on the specific database you use and the parameters you set for the search.
Learn more about rate here:
https://brainly.com/question/31784109
#SPJ11
in auto racing, a pit crew claims that its mean pit stop time (for 4 new times mph level) is less than 13 seconds. a random selection of 32 pit stop times has a
Answers
There is not enough evidence to support the claim made by the pit crew at α = 0.01.
From the question above, that n = 32, sample mean (X) = 12.9 seconds, standard deviation (s) = 0.19 seconds and level of significance (α) = 0.01
We need to check whether there is enough evidence to support the claim made by the pit crew at α = 0.01.
That means, we need to test the following hypotheses:
Null hypothesis: H₀: μ ≥ 13 (The mean pit stop time is greater than or equal to 13 seconds)
Alternate hypothesis: H1: μ < 13 (The mean pit stop time is less than 13 seconds)
This is a one-tailed test with the rejection region on the left side of the distribution. The critical value can be found using the t-distribution table with (n - 1) degrees of freedom at α = 0.01.
The degree of freedom is (n - 1) = 32 - 1 = 31
From the t-distribution table with 31 degrees of freedom and α = 0.01, we get the critical value t = -2.479.
The test statistic can be calculated using the formula:t = (X - μ) / (s / sqrt(n))
Substituting the given values, we get
t = (12.9 - 13) / (0.19 / sqrt(32))
t = -1.216
The calculated test statistic is -1.216.
It falls outside the rejection region (-2.479 to -∞) and therefore, we fail to reject the null hypothesis.
Therefore, there is not enough evidence to support the claim made by the pit crew at α = 0.01.
Your question is incomplete but most probably your full question was:
In auto racing, a pit crew claims that its mean pit stop time (for 4 new tires and fuel) is less than 13 seconds. A random selection of 32 pit stop times has a sample mean of 12.9 seconds and a standard deviation of 0.19 second.
Is there enough evidence to support the claim at α = 0.01?
Learn more about the mean at:
https://brainly.com/question/32334686
#SPJ11
A data warehouse allows users to specify certain dimensions, or characteristics. True or false
Answers
True, a data warehouse allows users to specify certain dimensions or characteristics.
In a data warehouse, dimensions represent the different aspects or characteristics by which data can be categorized or analyzed. These dimensions can include various attributes or variables that provide context and organize the data.
Users of a data warehouse can specify these dimensions based on their analytical needs and the nature of the data being stored.
For example, in a sales data warehouse, common dimensions may include product, customer, time, and location.
By specifying these dimensions, users can slice and dice the data based on different criteria and gain insights from various perspectives.
By defining dimensions, users can navigate through the data warehouse and perform multidimensional analysis using tools such as OLAP (Online Analytical Processing).
Dimensions provide a structure for organizing and querying data in a way that facilitates analysis and reporting.
In summary, a data warehouse allows users to specify dimensions or characteristics that help organize and analyze the data stored in the warehouse. These dimensions provide a framework for users to navigate and explore the data from different perspectives.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
determine the solutions of the equation: absolute value of the quantity one fifth times x plus 2 end quantity minus 6 equals two.
Answers
Answer: The solutions of the absolute value equation are given by:
x = -41 and x = 49.
What is the absolute value function?
The absolute value function is defined by:
|x| = x, x >= 0.
|x| = -x, x < 0.
The absolute value function measures the distance of a point x to the origin, that is, the distance to x = 0. From this, we get that |x| = a can mean either that:
x = a, or;
x = -a.
In this problem, the equation is given by:
Hence:
0.2|x - 4| = 9
|x - 4| = 45
The first possible solution is:
x - 4 = 45
x = 49.
The second possible solution is:
-x + 4 = 45
-x = 41
x = -41.
Hence the solutions are x = -41 and x = 49.
More can be learned about the absolute value function at brainly.com/question/24734454
Step-by-step explanation:
What is the area of this trapezoid?

Answers
Answer:
Area of trapezoid = 19.84 in^2
Step-by-step explanation:
Area of trapezoid = (b1+b2)/2 * Height
to find the height we have to use the Pythagorean formula for the left triangle
\(X^2 + Y^2 = Hypotenuse^2\)
we sub the values in the formula
\(3^2 = Y^2 + 4^2\)
Y = \(\sqrt{7}\) which the height of the triangle
now we sub the values in the trapezoid formula
Area of trapezoid = (5+10)/2 * sqrt{7}
Area of trapezoid = 19.84 in^2
Which of the following sets contains all the roots of a polynomial
F(x)=2x^3+x^2-3x
A- {0,1 3/2}
B- {-3/2, 1}
C- {-3/2, 0,1}
D- { -1, -3/2}
Answers
The set that contains all the roots of the polynomial is given by:
C. {-3/2, 0,1}
What are the roots of a polynomial F(x)?They are the values of x for which F(x) = 0.
In this problem, the polynomial is given by:
F(x) = 2x³ + x² - 3x.
Hence:
2x³ + x² - 3x = 0.
2x(x² + 0.5x - 1.5) = 0.
2x = 0 -> x = 0.
x² + 0.5x - 1.5 = 0 -> (x + 1.5)(x - 1) = 0.
Then, this means that the other two roots are:
x + 1.5 = 0 -> x = -1.5.x - 1 = 0 -> x = 1.Hence the correct option is:
C. {-3/2, 0,1}
More can be learned about the roots of a polynomial at https://brainly.com/question/2833285
#SPJ1
9. The amount of money Allen earns varies directly with the amount of time he works. He earns
$19 for working 2 hours. How much can Allen earn if he works 5 hours?
Answers
Answer:
47.5
Step-by-step explanation:
19÷2=9.5x5=47.5
Why is this correct? Please answer i have to turn in tomorrow

Answers
what’s the answer ??

Answers
The equation of the function is (d) g(x) = 4ˣ ⁻ ⁴ + 2
How to calculate the equation of the function g(x)From the question, we have the following parameters that can be used in our computation:
The functions f(x) and g(x)
In the graph, we can see that
f(x) = 4ˣ
The transformation on the graph is
The function f(x) is shifted up by 2 unitsThe function f(x) is shifted right by 4 unitsThis means that
g(x) = f(x - 4) + 2
Recall that
f(x) = 4ˣ
So, we have
g(x) = 4ˣ ⁻ ⁴ + 2
This means that the equation of the function is g(x) = 4ˣ ⁻ ⁴ + 2
Read more about transformation at
brainly.com/question/27224272
#SPJ1
Mickey used these calculations to find how much he would spend on 7 cartons of eggs, if 12 cartons of eggs cost $22.20. Describe his error.
12 cartons(+22.20)
--------------------------
$22.22(+22.20)
Unit price = $0.54 50.54(7) = $3.78
Answers
Answer:Mickey set up the equivalent rate wrong. The cartons of eggs should be in the denominator, because you need to find the unit price for 1 carton of eggs
Step-by-step explanation:
Answer:
Sample student response: Mickey set up the equivalent rate wrong. The cartons of eggs should be in the denominator, because you need to find the unit price for 1 carton of eggs.
Step-by-step explanation:
Using Rolle's theorem for the following function, find all values c in the given interval where f'(c) = 0. If there are multiple values, separate them using a comma. 45x2 f(x) = 2x3 + + 21x – 2 over 2 over (-4,2] 2 Provide your answer below: C=
Answers
There are no values of c in the interval where f'(c) = 0. Therefore, the answer is C = (no values)
To use Rolle's theorem, we need to check that the function is continuous on the closed interval [-4,2] and differentiable on the open interval (-4,2). Both conditions are satisfied by f(x) = (2x³ + 21x - 2)/2, so we can proceed with finding the values of c where f'(c) = 0.
First, we find the derivative of f(x):
f'(x) = 6x² + 21/2
Next, we set f'(x) = 0 and solve for x:
6x² + 21/2 = 0
6x² = -21/2
x² = -7/4
x = ±√(-7/4) = ±(i√7)/2
Since these values are not in the given interval (-4,2], we conclude that the correct option is C.
You can learn more about intervals at: brainly.com/question/13708942
#SPJ11
What is the perimeter of the composite figure?
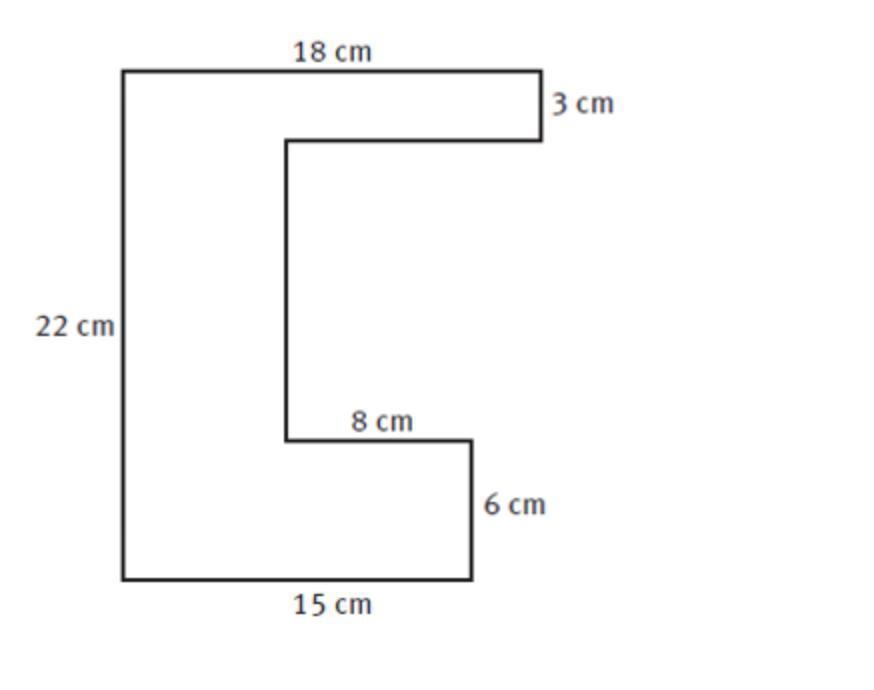
Answers
Answer: 96 cm
Step-by-step explanation:
The perimeter is the combined sum of the sides.
So 18 + 22 + 3 + 8 + 6 + 15 = 72
To find the 2 missing sides we use the information we already have.
On the top, we can see 18 is overall the largest line from the missing side.
So we'll need to subtract something from 18.
15 - 8 = 7 ( Inferencing )
18 - 7 = 11 ( length of the top missing side )
22 - 9 = 13
11 + 13 + 72 = 96 cm
Answer: The perimeter is 85 cm
Step-by-step explanation:
To find the perimeter you will need to add the distance around the shape.
But there seem to be one missing side .
To find that missing side we will have to add 3cm and 6 cm then subtract it from 22.
3 + 6 = 9
22 - 9 = 13
Now add the distance around the shape plus the 13.
22 + 15 + 6 + 8 + 13 + 3 + 18 = 85
A certain disease has an incidence rate of 0.2%. If the false negative rate is 4% and the false positive rate is 5%, compute the probability that a person who tests positive actually has the disease.
Answers
The probability that a person who tests positive actually has the disease is 3.8%.
The probability that a person who tests positive actually has the disease can be computed using Bayes' Theorem. Let D be the event that a person has the disease, and T be the event that a person tests positive.
Then, using Bayes' Theorem:
P(D|T) = P(T|D) * P(D) / [P(T|D) * P(D) + P(T|~D) * P(~D)]
where P(T|D) is the true positive rate (1 - false negative rate), P(T|~D) is the false positive rate, and P(D) is the incidence rate of the disease.
Substituting the given values:
P(D|T) = (0.996 * 0.002) / [(0.996 * 0.002) + (0.05 * 0.998)]
= 0.038
Therefore, the probability that a person who tests positive actually has the disease is 3.8%.
This calculation illustrates the importance of considering both the false positive and false negative rates when interpreting diagnostic test results.
A positive test result may not necessarily mean that a person has the disease, especially if the false positive rate is relatively high. In this case, the false positive rate of 5% means that 5 out of 100 people who do not have the disease would test positive, leading to a relatively low probability of actually having the disease given a positive test result.
To know more about probability, refer here:
https://brainly.com/question/12629667#
#SPJ11
How can I substitute this equation using a substitution method for b) y = 2x + 5
y = -3x - 10
Answers
Answer:
y = 2x + 5
y = -3x - 10= -23
Step-by-step explanation:
y = 2x + 5
y = -3x - 10 = -23
=====================================================
Explanation:
y = 2x+5 .... start with the first equation
-3x-10 = 2x+5 .... replace y with -3x-10 since y = -3x-10
The term "substitution" is the same as "replacement". Think of how the substitute teacher is a temporary replacement for your actual teacher.
Now we solve for x. Get all the x terms to one side and the non x terms to the other side
-3x-10 = 2x+5
-10-5 = 2x+3x
-15 = 5x
5x = -15
Next we divide both sides by 5 to isolate x
5x/5 = -15/5
x = -3
Now that we have the value of x, we can use this to find y. Pick any of the two equations to plug in this x value
y = 2x+5 = 2*(-3)+5 = -6+5 = -1
or
y = -3x-10 = -3(-3)-10 = 9-10 = -1
Either way, x = -3 leads to y = -1.
The fact we get the same y value helps us confirm we have the correct x value.
The solution to the system is (x,y) = (-3, -1)
This linear system is considered consistent and independent.
If you graph y = 2x+5 and y = -3x-10, you will find that the two lines intersect at (-3, -1) as the diagram shows below.

Let P(k) be a statement that 1/1*2+1/2*3+ ... + 1/k*(k+1)=
for: The basis step to prove P(k) is that at k = 1, _____ is true.
for:Show that P(1) is true by completing the basis step proof. Left side of P(k) and Right side of P(k)
for: Identify the inductive hypothesis used to prove P(k).
for: Identify the inductive step used to prove P(k + 1).
Answers
For: The basis step to prove P(k) is that at k = 1, _____ is true. for series .
What is series and sequence?
The foundational concepts in arithmetic are sequence and series. A sequence is an ordered collection of components where repetitions of any kind are permitted, but a series is the accumulation of all elements.
One of the many illustrations of a sequence or series is a mathematical progression.
Let P(k) be a statement that 1/1*2+1/2*3+ ... + 1/k*(k+1)=
The basis step to prove P(k) is that at k = 1, _____ is true.
Basic step - P(1) is true,
to show that 1/1.2 = 1/1+1
the left hand side of the equation is 1/1.2 = 1/2 right hand side
1/1 + 1 = 1/2
1/2 = 1/2
Learn more about sequence and series
brainly.com/question/12429779
#SPJ4
Rewrite each equation as y-k=a(x-h)^(2) or x-h=a(y-k)^(2). Find the vertex, focus, and directrix of the parabola.
10+5x=-(1-y)^2

Answers
\(\textit{horizontal parabola vertex form with focus point distance} \\\\ 4p(x- h)=(y- k)^2 \qquad \begin{cases} \stackrel{vertex}{(h,k)}\qquad \stackrel{focus~point}{(h+p,k)}\qquad \stackrel{directrix}{x=h-p}\\\\ p=\textit{distance from vertex to }\\ \qquad \textit{ focus or directrix}\\\\ \stackrel{"p"~is~negative}{op ens~\supset}\qquad \stackrel{"p"~is~positive}{op ens~\subset} \end{cases}\)
so hmm by looking at the expression, pretty much the squared variable is the "y" variable, namely the parabola is a horizontal parabola, let's put it in the vertex with focus point distance form as above
\(10+5x=-(1-y)^2\implies 10+5x=-(1-2y+y^2) \\\\\\ 10+5x=-(y^2-2y+1)\implies 10+5x=-(y-1)^2 \\\\\\ 5(2+x)=-(y-1)^2\implies 5(x+2)=-(y-1)^2\implies -5(x+2)=(y-1)^2 \\\\\\ \stackrel{4p}{-5}( ~~ x-(\stackrel{h}{-2}) ~~ )=(y-\stackrel{k}{1})^2\hspace{5em}\stackrel{vertex}{(-2~~,~~1)} \\\\[-0.35em] ~\dotfill\\\\ 4p=-5\implies p=-\cfrac{5}{4}\)
well, first off, let's notice that the "p" distance is negative, meaning the horizontal parabola is opening to the left, so hmmm if we move from the vertex 5/4 to the left, we'll ge the focus point, and 5/4 to the right, we'll get the directrix equation.
\(-2-\cfrac{5}{4}\implies -\cfrac{13}{4}\implies -3\frac{1}{4}\hspace{10em}\stackrel{focus~point}{\left( -3\frac{1}{4}~~,~~1 \right)} \\\\[-0.35em] ~\dotfill\\\\ -2+\cfrac{5}{4}\implies -\cfrac{3}{4}\hspace{16em}\stackrel{directrix}{x=-\cfrac{3}{4}}\)
Check the picture below.

The required vertex, focus, and directrix are (-2, 1), (-13/4, 1) and -3/5 respectively,
Given that,
To Find the vertex, focus, and directrix of the parabola, when 10+5x=-(1-y)² and Rewrite each equation as y-k=a(x-h)² or x-h=a(y-k)²
A parabola is a cross-section cut out of the cone and represented by an equation
Here,
The standard equation in the parabola,
(x - h) = a(y - k)²
Now given the equation,
10 + 5x = -(1 - y)²
5(x + 2 ) = - (1 -y)²
(x - (-2)) = -1/5 (y - 1)²
where, h = -2, k = 1 and a = -1/5 or 4p = -5, p = -5/4 .
So vertex = (-2, 1)
Focus = (-2 - 5/4, 1)
Focus = (-13/4, 1)
Directrix = h - p
Directrix = -2 + 5/4
Directrix = -3/5
Thus, the required vertex, focus, and directrix are (-2, 1), (-13/4, 1) and -3/5 respectively.
Learn more about parabola here:
brainly.com/question/4074088
#SPJ2
is anyone able to answer this for me? GIVING BRAINLIEST! hurry!


Answers
1
5
17
53
161
Ian’s pattern:
0
1
3
7
15
Ordered pair:
(1, 0)
(5, 1)
(17, 3)
(53, 7)
(161, 15)
Table 1 -
Sequence 1:
9
11
13
15
17
Sequence 2:
5
8
11
14
17
Ordered pair:
(9, 5)
(11, 8)
(13, 11)
(15, 14)
(17, 17)
Table 2 -
Sequence 1:
20
16
12
8
4
Sequence 2:
20
17
14
11
8
Ordered pair:
(20, 20)
(16, 17)
(12, 14)
(8, 11)
(4, 8)
Table 3 -
Sequence 1:
1
3
7
15
31
Sequence 2:
40
24
16
12
10
Ordered pair:
(1, 40)
(3, 24)
(7, 16)
(15, 12)
(31, 10)
4x^2-15x-4
factorise please
Answers
______________________________
1.) Change the equation using factored transformation: \(4x^2-15x-4=0\)- Quadratic polynomial can be factored using the transformation \(ax^2+bx+c=a(x-x_{1})(x-x_{2})\), where \(x_{1}\) and \(x_{2}\) are the solutions of the quadratic equation \(ax^2+bx+c=0\).
- This steps basically means change you current equation using the formula \(ax^2+bx+c=0\).
2.) Turn the factored form into the quadratic equation form:\(x=\frac{-(-15)\frac{+}{}\sqrt{(-15)^2-4\bold{x}4(-4)}}{2\bold{x}4}\)- All equations of the form \(ax^2+bx+c=0\) can be solved using the quadratic formula: \(\sqrt{\frac{-b\frac{+}{}\sqrt{b^2-4ac}}{2a} }\).
- The quadratic equation formula gives two solutions, one when \(\frac{+}{}\) is addition and one when it is subtraction.
3.) Square -15:\(-15^2=225\)
Equation at the end of Step 3:
\(x=\frac{-(-15)\frac{+}{}\sqrt{225-4\bold{x}4(-4)}}{2\bold{x}4}\)4.) Multiply −4 times 4:\(-4\) × \(4=-16\)Equation at the end of Step 4:
\(x=\frac{-(-15)\frac{+}{}\sqrt{225-16(-4)}}{2\bold{x}4}\)5.) Multiply −16 times −4:\(-16\) × \(-4=64\)Equation at the end of Step 5:
\(x=\frac{-(-15)\frac{+}{}\sqrt{225+64}}{2\bold{x}4}\)6.) Add 225 to 64:\(225+64=289\)Equation at the end of Step 6:
\(x=\frac{-(-15)\frac{+}{}\sqrt{289}}{2\bold{x}4}\)7.) Take the square root of 289:\(\sqrt{289}=17\)Equation at the end of Step 7:
\(x=\frac{-(-15)\frac{+}{}17}{2\bold{x}4}\)8.) Change -15 to positive 15:\(-15=15\)Equation at the end of Step 8:
\(x=\frac{15\frac{+}{}17}{2\bold{x}4}\)9.) Multiply 2 by 4:\(2\) × \(4=8\)Equation at the end of Step 9:
\(x=\frac{15\frac{+}{}17}8}\) 10.) Now Solve:Now solve the equation \(x=\frac{15\frac{+}{}17}8}\) when \(\frac{+}{}\) is plus.
Add 15 to 17:
\(15+17=32\)\(x=\frac{32}{8}\)Divide 32 by 8:
\(32\) ÷ \(8=4\)\(x=4\)Now solve the equation \(x=\frac{15\frac{+}{}17}8}\) when \(\frac{+}{}\) is minus.
Subtract 15 by 17:
\(15-17=-2\)\(x=\frac{-2}{8}\)Reduce the fraction to lowest terms by extracting and canceling out 2:
\(-2\) ÷ \(-2=-1\) \(8\) ÷ \(-2=-4\)\(x=-\frac{1}{4}\)11.) Factor the expression:Factor the original expression using \(ax^2+bx+c=a(x-x_{1})(x-x_{2})\). Substitute 4 for \(x_{1}\) and \(-\frac{1}{4}\) for \(x_{2}\):
\(4x^2-15x-4=4(x-4)(x-(-\frac{1}{4}))\)Simplify all the expressions of the form \(p-(-q)\) to \(p+q\):
\(4x^2-15x-4=4(x-4)(x+\frac{1}{4})\)Add \(\frac{1}{4}\) to x by finding a common denominator and adding the numerators. Then reduce the fraction to lowest terms if possible:
\(4x^2-15x-4=4(x-4)\bold{x}(\frac{4x+1}{4})\)Cancel out 4, the greatest common factor in 4 and 4:
\(4x^2-15x-4=(x-4)(4x+1)\)______________________________
Convert 2 grams into milligrams.
*Note: you must use these exact conversion factors to get this question right.
1 pound (lb) = 16 ounces (oz)
1 kilogram (kg) = 1000 grams (g)
1 ton (ton) = 2000 pounds (lb)
1 ounce (oz) = 28.35 grams (g)
1 gram (g) = 1000 milligrams (mg)
1 pound (lb) = 0.454 kilograms (kg)

Answers
2 grams = 2000 milligrams
Conversion between different units of measurement of the same quantity is called as conversion of units.
The process of conversion depends on the specific situation and the precision and accuracy of measurement.
Conversions from one unit to another should be exact, without changing the precision of the first. This is sometimes called soft conversion. It does not involve changing of the physical configuration of the unit being calculated.
'g' is the same as grams and similarly 'mg' is the same as milligrams.
Thus, when asked to convert 2 g to mg, as in the given question,
first multiply the value in grams by the conversion factor '1000'.
So, 2 grams = 2 × 1000 = 2000 milligrams.
A gram is larger unit than a milligram.
To know more about conversion of units, refer
https://brainly.com/question/97386
#SPJ13