The circumference of a hula hoop is 86\pi \text{ cm}86π cm86, pi, start text, space, c, m, end text. What is the radius of the hula hoop? \text{cm}cm
Answers
Answer:
43 cmStep-by-step explanation:
Circumference formula:
C = 2πrGiven:
C = 86πFind r:
r = C/2π = 86π / 2π = 43 cmNow
ATQ
\(\\ \rm\Rrightarrow C=2\pi r\)
\(\\ \rm\Rrightarrow 2\pi r=86\pi\)
\(\\ \rm\Rrightarrow r=\dfrac{86\pi}{2\pi}\)
\(\\ \rm\Rrightarrow r=\dfrac{86}{2}\)
\(\\ \rm\Rrightarrow r=43cm\)
Related Questions
select the appropriate reagents for the transformation at −78 °c.
Answers
For the transformation at -78 °C, appropriate reagents include lithium aluminum hydride (LiAlH4) and diethyl ether.
What reagents are suitable for -78 °C transformations?At -78 °C, certain chemical reactions require the use of specific reagents to achieve the desired transformation. One commonly used reagent is lithium aluminum hydride (LiAlH4), which acts as a strong reducing agent. It is capable of reducing various functional groups, such as carbonyl compounds, to their corresponding alcohols.
Diethyl ether is typically employed as a solvent to facilitate the reaction and ensure efficient mixing of the reactants. Researchers often utilize this low temperature for reactions involving sensitive or reactive intermediates, as it helps control the reaction and prevent unwanted side reactions.
The use of LiAlH4 and diethyl ether provides a reliable combination for achieving the desired transformation at this temperature, enabling chemists to manipulate and modify compounds in a controlled manner.
Learn more about reagents
brainly.com/question/28504619
#SPJ11
. (3, 6) and (6,9)
slope of the line
Answers
Answer:
1
Step-by-step explanation:
→ Write down slope formula
\(\frac{y2-y1}{x2-x1}\)
→ Identify the values
y₂ = 9, y₁ = 6, x₂ = 6 and x₁ = 3
→ Substitute in values into formula
\(\frac{9-6}{6-3}\)
→ Simplify
1
Write an equation in terms of x and y for the function that is described by the given characteristics. a cosine curve with a period of , an amplitude of 1, a left phase shift of , and a vertical translation down by 9/2 of a unit.
Answers
The equation for the described function can be written as:
y = cos(x - π) - 9/2
Let's break down the components of the equation:
The cosine function, cos(x), produces a periodic wave with an amplitude of 1.
The period of the cosine curve is determined by the coefficient in front of the angle, which is 1 in this case. A period of 1 corresponds to one complete cycle of the cosine curve.
The left phase shift of π shifts the entire curve to the right by π units.
The vertical translation down by 9/2 units shifts the entire curve downwards by 9/2 units.
Therefore, the equation y = -cos(x - π) - 9/2 represents a cosine curve with the given characteristics.
Learn more about the cosine curve here
brainly.com/question/13516498
#SPJ4
Please Help! Ill give brainliest no fakes PLEASE!!

Answers
Answer:
4 and then 15
Step-by-step explanation:
second one: 6:4
last one: 15:10
How do I solve 18=6(2x-8)
Answers
Answer:
x= 5.5
Step-by-step explanation:
18=12x-48
-12x= -48-18
-12x= -66
x= -66/-12
x= 5.5
Answer:
Okay so first you distribute 6 into the parenthesis that gives you
18=12x-48
Then you add 48 on both sides
66=12x
then you divide
X=5.5
Step-by-step explanation:
What is the angle between the vectors − 2i 3j k and i 2j − 4k?
Answers
The angle between the vectors can be found using the dot product. The formula is θ= |A| =√(x12 + y12 + z12) The angle between the vectors -2i + 3j + k and i + 2j - 4k is approximately 137.8 degrees.
v1 • v2 = (-2i + 3j + k) • (i + 2j - 4k)
= -2 - 6 + 1 = -7
|v1| = \(\sqrt{((-2)^2 + 3^2 + 1^2)}\)
=\(\sqrt{(4 + 9 + 1)}\)
=\(\sqrt{14}\)
|v2| = \(\sqrt{((1)^2 + 2^2 + (-4)^2)}\)
= \(\sqrt{(1 + 4 + 16) }\)
= (\(\sqrt{21}\)
θ= |A| (-7/\(\sqrt{14}\)\(\sqrt{21}\))
= |A| (-7/21*14)
= |A|(-7/294)
= 137.8 degrees
The angle between two vectors can be found using the dot product formula. This formula isθ= |A| =√(x12 + y12 + z12). In the case of the vectors -2i + 3j + k and i + 2j - 4k, this formula can be used to find the angle between them. The dot product of the two vectors is -2 - 6 + 1 = -7. The magnitude of the first vector, |v1|, can be found using the Pythagorean theorem, which is
\(\sqrt{((-2)^2 + 3^2 + 1^2)}\)
= \(\sqrt{(4 + 9 + 1)}\)
= \(\sqrt{14}\).
The magnitude of the second vector, |v2|, can be found using the Pythagorean theorem, which is
\(\sqrt{((1)^2 + 2^2 + (-4)^2)}\)
= \(\sqrt{(1 + 4 + 16)}\)
= \(\sqrt{21}\)
Once the dot product and magnitudes are known, the angle between the two vectors can be found using the formula .Therefore, the angle between the two vectors is approximately 137.8 degrees.
Learn more about vector here
https://brainly.com/question/15709504
#SPJ4
.Specifications for a piece of material used in the manufacture of a bed mattress require that the piece be between 63.76 and 64.24 inches. The process that produces the piece yields a mean of 64 and a standard deviation of 0.1 inches. The distribution of output is normal. What percentage of the pieces will meet the length specs?
Answers
The correctanswer is-the percentage of the pieces that will meet the length specs is 98.78%.
The given data may be a random variable that takes after the normal distribution with mean μ=64 and standard deviation σ=0.1
The required value is to discover the rate of the pieces that will meet the length specs which is between 63.76 and 64.24 inches.
To find the required percentage, standardize the given limits as follows: Lower Limit: (63.76 - μ) / σ= (63.76 - 64) / 0.1 = -2.4
Upper Limit: (64.24 - μ) / σ= (64.24 - 64) / 0.1 = 2.4
Using the Standard Normal Distribution Table, the probability that the value will fall between -2.4 and 2.4 is found to be 0.9878.
The required percentage is then found by multiplying the probability by 100, which is: Percentage = 0.9878 x 100% = 98.78%
Therefore, the percentage of the pieces that will meet the length specs is 98.78%.
know more about Normal Distribution
https://brainly.com/question/15103234
#SPJ11
1. (The first paragraph provides some context that I hope makes the problem more interesting, but the information in this paragraph is not necessary to correctly answer the questions below.) Suppose you work for an automotive manufacturer and are setting terms for a new vehicle leasing program. In particular, the manufacturer must set the lease-end residual value for the lease contract; this is the expected value of the vehicle at the end of the lease period. The lease customer ("lessee") could choose to purchase the vehicle at this price at the end of the lease. - If the manufacturer sets the lease-end residual value too low, then it gives the lessee a windfall (the lessee could purchase the car and resell it at a higher price). - If the manufacturer sets the lease-end residual value too high, then it discourages leasing because the customer cost (down payment and lease payments) will be higher. Suppose we have determined that for a vehicle with a retail price of 40 thousand dollars when new and which is driven 12,000 miles per year and which receives all recommended maintenance, the market value of the vehicle after t years of service is given by (1) y=40exp(−0.025−0.2t)=40e
−0.025−0.2t
Where market value y is measured in thousands of dollars; e.g., y=20 means $20,000 market value. A. Using non-linear equation (1), calculate the market value y after three years of service (t=3) and after five years of service. Further, calculate the simple (discrete) proportional change in y when the vehicles goes from three years of service to five years of service (i.e., the market value with three years of service is the base for the calculation). B. Apply the natural log transformation to equation (1). Does the transformed equation exhibit constant marginal effect? Explain briefly. C. (i) Use the slope term from your transformed equation from part B to directly calculate the continuous proportional change in y when years of service increases from three years to five years. decreases from $2.50 to $2.
Answers
The continuous proportional change in y when years of service increases from three years to five years is:Δy/y = (y_5 - y_3) / y_3= e^(ln(y_5) - ln(y_3)) / y_3= e^(-0.2Δt) = e^(-0.2*2)= e^(-0.4)≈ 0.6703The proportional change in y when years of service increases from three years to five years is approximately 0.6703.
A. Using non-linear equation (1), we are to calculate the market value y after three years of service (t=3) and after five years of service. Further, calculate the simple (discrete) proportional change in y when the vehicles go from three years of service to five years of service (i.e., the market value with three years of service is the base for the calculation).Given equation is y = 40e^(-0.025-0.2t)Where t = 3, the market value y is:y = 40e^(-0.025-0.2(3))= 40e^(-0.625)= 22.13 thousand dollarsWhere t = 5, the market value y is:y = 40e^(-0.025-0.2(5))= 40e^(-1.025)= 14.09 thousand dollarsSo, the discrete proportional change in y when the vehicles go from three years of service to five years of service is:proportional change in y = (y_5 - y_3) / y_3 * 100%= (14.09 - 22.13) / 22.13 * 100%= -36.28%B. We need to apply the natural log transformation to equation (1).
Therefore, we take the natural log of both sides of the equation.y = 40e^(-0.025-0.2t)ln(y) = ln(40e^(-0.025-0.2t))= ln(40) + ln(e^(-0.025-0.2t))= ln(40) - 0.025 - 0.2tSo, we get the transformed equation as:ln(y) = -0.025 - 0.2t + ln(40)Now, let's take the derivative of both sides of this transformed equation, with respect to t. We get:1 / y * dy/dt = -0.2This equation doesn't exhibit constant marginal effect because dy/dt depends on y. Therefore, we can't say that a one unit increase in x would always lead to the same proportional change in y.C. (i) Use the slope term from your transformed equation from part B to directly calculate the continuous proportional change in y when years of service increases from three years to five years. Given transformed equation is:ln(y) = -0.025 - 0.2t + ln(40)When years of service increases from three years to five years, then change in t is:Δt = 5 - 3 = 2
for more search question proportional
https://brainly.com/question/870035
#SPJ8
Yvonne is using a coordinate grid cor the first time. She wants to find the location of the ordered pair (3 ,7) on the grid. Starting at the origin , which movement should Yvonne do first? A- Move right along the x-axis to 3 B- Move up right along the y-axis to 7 C- Move right along the y-axis to 7 D- Move up along the x-axis to 7
Answers
Answer:
6,3
Step-by-step explanation:
Please help I'm begging a ACE OR GENES To help me please please help please please ASAP please please help please please ASAP please please help

Answers
Answer:
3/2
Step-by-step explanation:
WX/AB = 12/8 = 3/2
Answer: 3/2
Which table represents a function?

Answers
Answer:
Table 4 represents a function because each x-value corresponds to exactly one y-value.
To investigate the relationship between age and preference for two new building plans on city property, a random sample of city residents was surveyed. The residents were asked whether they preferred the city build a new condominium project to increase the city revenue or a new park. Each resident was classified into one of three age groups (under 25, 25-40, over 40). The test statistic for the appropriate hypothesis test was 4.108. Approximately what is the probability that the observed responses would be as far or farther from the expected responses if there is no association between age-group and preference
Answers
The approximate probability that the observed responses would be as far or farther from the expected responses if there is no association between age-group and preference is approximately 0.1282.
To determine the probability that the observed responses would be as far or farther from the expected responses if there is no association between age-group and preference, we need to calculate the p-value associated with the test statistic.
Since the p-value is not provided directly, we cannot determine the exact probability. However, we can make an estimation based on the given options.
The p-value represents the probability of obtaining a test statistic as extreme or more extreme than the observed value, assuming no association between the variables. A smaller p-value indicates stronger evidence against the null hypothesis of no association.
Among the given options, the smallest value is 0.0001. If this were the correct option, it would suggest a very small probability of the observed responses occurring by chance alone if there were no association.
To make an estimation, we typically compare the p-value to a significance level (usually 0.05) to determine statistical significance. If the p-value is smaller than the significance level, we reject the null hypothesis in favor of the alternative hypothesis.
Based on the options provided, the closest value to the conventional significance level of 0.05 is 0.1282. This suggests that if the p-value associated with the test statistic of 4.108 is approximately 0.1282 or larger, the observed responses would not be considered statistically significant, and we would fail to reject the null hypothesis of no association between age-group and preference.
For more such questions on probability
https://brainly.com/question/23417919
#SPJ8
A list of numbers ordered from least value to greatest value is
shown. One number is missing.
18, 3.71, ____, V17
5
Which number could be the missing number?
A 4.5
B 3.8%
C
57
15
D (3.9) ²
Answers
Answer:
Step-by-step explanation:
The answer is A 4.5.
To determine this, we need to look at the given numbers and find the missing number that would fit logically in the sequence. We can see that the numbers are ordered from least to greatest and that the missing number falls between 3.71 and V17.
Option A, 4.5, falls within this range and could logically be the missing number. Options B, C, and D are not within this range and do not fit logically in the sequence.
Solve for x.
18 - X= 5
A.X=-13
B.x= 23
C.x= 13
D.x = -23
Answers
A surveyor measures the angle of elevation to a point on a mountain to be 12. The point on the mountain is horizontally 5 miles away from the surveyor. The vertical change in elevation from the point where the surveyor is standing to the point on the mountain is _____ miles. (Round your answer to the nearest hundredth of a mile.)
Answers
The vertical change in elevation is 1.06 miles.
The angle of elevation is an angle that is formed between the horizontal line and the line of sight. If the line of sight is upward from the horizontal line, then the angle formed is an angle of elevation.
From the right triangle formed, the adjacent side to the angle of elevation is 5 miles and the vertical change in elevation is the opposite side. From the trigonometric function, the tangent of an angle,
tan 12° = x / 5 miles
The value of x from the equation is 1.06 miles.
Thus, the vertical change in elevation is 1.06 miles.
To know more about elevation visit: brainly.com/question/29477960
#SPJ4
The vertical change in elevation from the point where the surveyor is standing to the point on the mountain = 1.06 miles
Here, angle of elevation θ = 12°
Let y be the the vertical change in elevation from the point where the surveyor is standing to the point on the mountain and x be the horizontal distance between the point on the mountain and the surveyor.
x = 5 miles
We need to find the value of y.
Consider tangent of angle of elevation θ
tan(θ) = y/x
tan(12°) = y/5
0.2126 = y/5
y = 0.2126 × 5
y = 1.06 miles
So, the vertical change in elevation = 1.06 miles
Learn more abot the angle of elevation here:
https://brainly.com/question/21137209
#SPJ4
Solve.
y=3x – 4
9x – 3y = 14
Use the substitution method.
O The solution is (12, 14).
O The solution is (14, 12)
O There is no solution.
O There are an infinite number of solutions.
please please please hurry i really need help
Answers
Answer:
The answer is 12,14
Step-by-step explanation:
hope this helps
gravel is being dumped from a conveyor belt at a rate of 10 cubic feet per minute. it forms a pile in the shape of a right circular cone whose base diameter and height are always equal. how fast is the height of the pile increasing when the pile is 25 feet high?
Answers
Below is the answer
Learn more about circular cone at https://brainly.com/question/30355649
#SPJ4

Evaluate the limit or determine that it does not exist. (Give an exact answer. Use symbolic notation and fractions where needed. Enter DNE if the limit does not exist.)
lim ( x , y ) → ( 0 , 0 ) ( x + y + 3 ) e ^ (− 1 / ( x ^ 2 + y ^ 2 )) =
Answers
The limit exists and the exact answer is 0.
To evaluate the limit or determine that it does not exist, we need to find the value of the function as (x,y) approaches (0,0).
lim ( x , y ) → ( 0 , 0 ) ( x + y + 3 ) e ^ (− 1 / ( x ^ 2 + y ^ 2 ))
First, we can simplify the expression by substituting (0,0) for (x,y):
lim ( 0 , 0 ) → ( 0 , 0 ) ( 0 + 0 + 3 ) e ^ (− 1 / ( 0 ^ 2 + 0 ^ 2 ))
This simplifies to:
lim ( 0 , 0 ) → ( 0 , 0 ) ( 3 ) e ^ (− 1 / 0 )
As the denominator in the exponent approaches 0, the value of the exponent approaches negative infinity. This means that the value of e to the negative infinity approaches 0:
lim ( 0 , 0 ) → ( 0 , 0 ) ( 3 ) ( 0 )
The limit of this expression is 0, so the limit of the original expression is also 0:
lim ( x , y ) → ( 0 , 0 ) ( x + y + 3 ) e ^ (− 1 / ( x ^ 2 + y ^ 2 )) = 0
For more similar questions on limit:
brainly.com/question/12017456
#SPJ11
a x b = 60 work out the value of 4b/a
Answers
Answer:
240/a^2
Step-by-step explanation:
4b/a=240/a^2 we can't find it's value in numbers. if a=1 then b=60
if a=2 then. b=30 etc.
Use the dice lattice shown below to answer the question that follows.
When Martha rolled the dice 36 times, she got a sum of 8 seven times. Explain why Martha's
experimental probability is different than a theoretical probability.
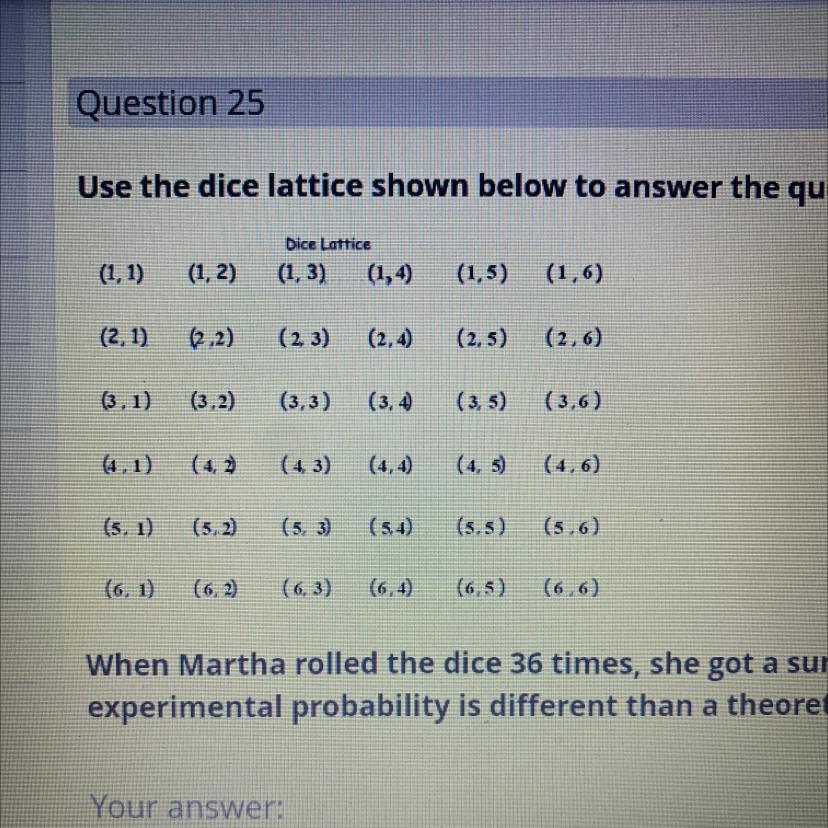
Answers
Answer:
Theoretical probability is what is expected and experimental probability is the answer.
Step-by-step explanation:
Theoretical probability is what you expected the answer to be. In reality the experimental probability is the actual answer.
i need help with this lol

Answers
Answer:
32 i think
Step-by-step explanation:
hi guys can you guys answer this pls and explain plss

Answers
Answer:
Symmetry is correspondence of the form and arrangement of elements or parts on opposite sides of a dividing line. imagine that this ractangle is a piece of paper, you need to fold it two times, different ways. in this case when you fold it over the horizontal colored line all colored parts will match, same case when you fold it vertically.

The Cartesian coordinate system can be applied to three-dimensional solids. Instead of two axes, the coordinate system has three. What are the labels? Check all that apply.
A. z
B. y
C. a
D. x
E. w
Answers
Answer:
its z y and x
Step-by-step explanation:
can i pls get brainliest
Let (X, Y) denote a uniformly chosen random point inside the
unit square
[0, 2]2 = [0, 2] × [0,2] = {(x, y) : 0 ≤ x, y ≤
2}.
What is the probability P(|X−Y| ≤ 1/2)?
Answers
The probability P(|X - Y| ≤ 1/2) is equal to 1 or 100%.
To find the probability P(|X - Y| ≤ 1/2), we need to determine the area of the region where the absolute difference between X and Y is less than or equal to 1/2.
Consider the unit square [0, 2] × [0, 2]. We can divide it into two triangles and two rectangles:
Triangle A: The points (x, y) where x ≥ y.
Triangle B: The points (x, y) where x < y.
Rectangle C: The points (x, y) where x ≥ y + 1/2.
Rectangle D: The points (x, y) where x < y - 1/2.
Let's calculate the areas of these regions:
Area(A) = (base × height)/2 = (2 × 2)/2 = 2
Area(B) = (base × height)/2 = (2 × 2)/2 = 2
Area(C) = 2 × (2 - 1/2) = 3
Area(D) = 2 × (2 - 1/2) = 3
Now, let's calculate the area of the region where |X - Y| ≤ 1/2. It consists of Triangle A and Triangle B, as both triangles satisfy the condition.
Area(|X - Y| ≤ 1/2) = Area(A) + Area(B) = 2 + 2 = 4
Since the total area of the unit square is 2 × 2 = 4, the probability P(|X - Y| ≤ 1/2) is the ratio of the area of the region to the total area:
P(|X - Y| ≤ 1/2) = Area(|X - Y| ≤ 1/2) / Area([0, 2]2) = 4 / 4 = 1
Therefore, the probability P(|X - Y| ≤ 1/2) is equal to 1 or 100%
To know more about probability refer here:
https://brainly.com/question/32560116?#
#SPJ11
Without using the formula, work out the gradient of the graph shown.

Answers
Answer:
1/3
Step-by-step explanation:
i really need help with this please!! i need it by 12:00 tonight

Answers
Passes through (-3,7) and has vertex (-5,4)
Answers
Answer:
y
=
−
3
x
2
+
30
x
−
71
Explanation:
the equation of a parabola in
vertex form
is.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
∣
∣
∣
2
2
y
=
a
(
x
−
h
)
2
+
k
2
2
∣
∣
∣
−−−−−−−−−−−−−−−−−−−−−
where
(
h
,
k
)
are the coordinates of the vertex and a
is a multiplier
here
(
h
,
k
)
=
(
5
,
4
)
⇒
y
=
a
(
x
−
5
)
2
+
4
to find a substitute
(
7
,
−
8
)
into the equation
−
8
=
4
a
+
4
⇒
a
=
−
3
⇒
y
=
−
3
(
x
−
5
)
2
+
4
←
in vertex form
distributing and simplifying gives
y
=
−
3
(
x
2
−
10
x
+
25
)
+
4
y
=
−
3
x
2
+
30
x
−
75
+
4
⇒
y
=
−
3
x
2
+
30
x
−
71
←
in standard form
Step-by-step explanation:
5 solve the literal equation 2y = x+3 for x
Answers
Answer:
\(x=2y-3\)
Step-by-step explanation:
So we have the equation:
\(2y=x+3\)
And we want to solve it for x. In other words, we want to isolate the x-variable. To start, first subtract 3 from both sides. The right side cancels:
\((2y)-3=(x+3)-3\\2y-3=x\)
And, that's it :)
If preferred, we can also switch the equation around using the symmetric property:
\(x=2y-3\)
Answer:
\(\Large \boxed{\sf{x=2y-3}}\)
Step-by-step explanation:
\(\sf We \ have \ the \ equation: \\ \\ 2y = x+3 \\ \\ We \ need \ x \ on \ one \ side \of \ the \ equation. \\ Solve \ for \ x. \\ \\ Subtract \ 3 \ from \ both \ sides. \\ \\ 2y-3=x+3-3 \\ \\ Simplify \ the \ equation. \\ \\ 2y-3=x\)
The critical value approach specifies a region of values, called the ______. If the test statistic falls into this region, we reject the ______.
Answers
The critical value approach specifies a region of values, called the critical region or rejection region. If the test statistic falls into this region, we reject the null hypothesis.
In hypothesis testing, the critical value approach is a method used to determine whether to reject or fail to reject the null hypothesis. This approach involves specifying a level of significance, alpha (α), which is the maximum probability of making a Type I error (rejecting the null hypothesis when it is true).
Learn more about null hypothesis
https://brainly.com/question/28920252
#SPJ4
Please help me on this, I'm really stuck. It would also be awesome if you elaborated on how you got the Lower Quartile (LQ) and Upper Quartile (UQ).
IQR - Inner Quartile Range

Answers
All statements are true except last statement is false
What is Inner quartile range and its formula?The inner quartile range (IQR) is a measure of statistical dispersion, which is the spread of data. The formula to find the inner quartile range takes the value of the third quartile and subtracts the value of the first quartile. Similarly, the inner quartile range is the range between the 75th and 25th percentiles (75 - 25 = 50% of the data).
We can make the following observations from this boxplot:
IQR is 6
5 represents the number of students in or below the lowest quartile
each share is 25%
The median is greater than the IQR
You can find the IQR by finding the difference between the upper and lower quartiles
If a new student moved into the classroom and read 25 books, that would increase the selection
Therefore, the following statements are true:
IQR is 6
5 represents the number of students in or below the lowest quartile
each share is 25%
The median is greater than the IQR
You can find the IQR by finding the difference between the upper and lower quartiles
If a new student moved into the classroom and read 25 books, that would increase the selection
The following statement is false:
Most data represents 10 or more books (since most data appears to be 0-8 books)
Learn more about inner quartile range here
https://brainly.com/question/30368446
#SPJ1