The area of the shaded region is 42 ft2 . What is the area of the unshaded region? A) 7 ft 2B) 21 ft2C) 42 ft2D) 84 ft2


Answers
Area of a Rectangle
Given a rectangle of width W and length L, its area can be calculated as:
\(A=W\cdot L\)If we cut the rectangle by its diagonal, we get to congruent triangles, each one with half the area of the rectangle, that is:
\(A_t=\frac{A}{2}_{}\)The shaded region corresponds to one of these triangles, thus the unshaded region must have the same area as the shaded region.
Area of the shaded region: 42 ft2
Area of the unshaded region: 42 ft2
Area of the rectangle: 84 ft2
Related Questions
What percent of students prefer to watch football on the weekend?
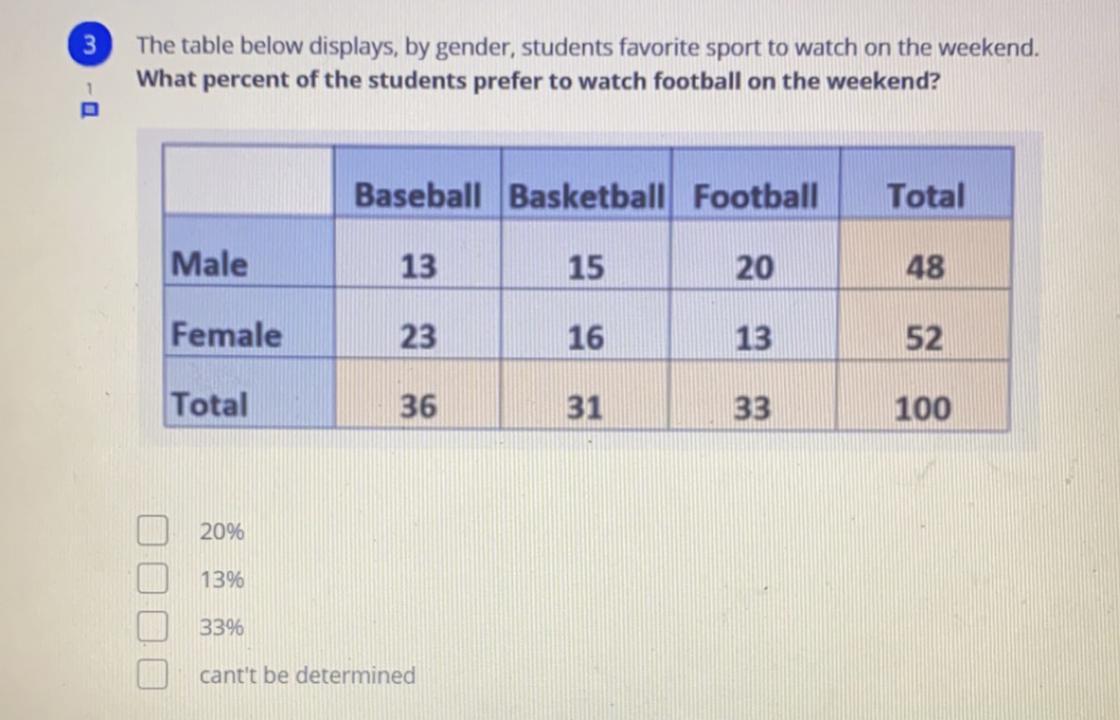
Answers
Answer:
20%
Step-by-step explanation:
48+52=100
20 out of 100= 20
Tina baked some cookies. 12 of her cookies were peanut butter. 12 of the peanut butter cookies also had chocolate chips. What fraction of the cookies were peanut butter and had chocolate chips?
Answers
Answer:
12/12 or 1
Step-by-step explanation:
Tina baked 12 peanut butter cookies, and it is said that 12 of them had chocolate chips. So, we can make a fraction, being 12/12
A robot can complete 6 tasks in 7/10 hour. Each task takes the same amount of time. a. How long does it take the robot to complete one task? b. How many tasks can the robot complete in one hour?
Answers
Answer:
7/60 hour or 7 minutes b) 8 or 8 4/7 depending if you consider a fraction of a task is yes or no
Step-by-step explanation:
Tessellations
Determine whether the given figure tessellates the plane.
a. yes
b. no
Please select the best answer from the choices provided

Answers
Answer:
B. No
Step-by-step explanation:
I calculated it logically
Identify the graph of the inequality 2(2x-1)+7< 13 or -2x+5-10.

Answers
From the resulting solution, the correct linear inequality graph is Graph C.
Solving inequality expressionGiven the inequality equation below:
2(2x-1)+7< 13 or -2x+5 ≤ -10.
Simplify the expression
2(2x-1)+7< 13
Expand
4x - 2 + 7 < 13
4x + 5 < 13
4x < 13 - 5
4x < 8
x < 2
For the inequality -2x+5 ≤ -10.
-2x+5 ≤ -10
-2x ≤ -15
x ≥ 7.5
Hence the solution to the given system of inequalities are x < 2 and x ≥ 7.5
Learn more on inequality graph here: https://brainly.com/question/24372553
#SPJ1
help please help please

Answers
Step-by-step explanation:
first choice
ggiteesxdgcJ gray y atcha
a car rental company charges a daily rate of $22 plus $.10 per mile for a certain car. suppose that you rent that car for a day and your bill (before taxes) is "$55." how many miles did you drive?
Answers
Answer:
330 miles
Step-by-step explanation:
Use the slope intercept form of a line.
y = mx + b
b will be the constant or the daily cost to rent the car. The x is the number of miles. The y is the total cost and the m is the cost per mile.

Give the coordinates of point D.
A. (-2,-4)
B. (-4,2)
C. (-4,-2)
D. (4, -2)

Answers
explanation:
Which statement is true about the graph of the line 8x+3y=0It is a vertical lineIt is a horizontal lineIt passes through (8,3)It passes through the origin
Answers
Vertical ine is in the form
x = a where a is a number
Horizontal line is in the fomr
y = b, where b is a number
Clearly the equatin isn't a vertical or hirzontal line.
Now, 3rd and 4th hoice evaluate:
(8,3) --- point it passes
let's plug in:
8x + 3y
8(8) + 3(3) = 0 ??? NO!!
T
This choice is not right.
Now, 4th choice:
passes through origin (0,0)
8x + 3y = 0
Now plugging in:
8(0) + 3(0)
= 0
So, this is correct.
It passes through the origin
number 4 pls help plssssssssssssss I will pay u plssssssssssss help me out. its number 4

Answers
Answer:
40%
Step-by-step explanation:
i used a calculator
1. ALUMMUNI PLC. Produces three models of tractors: Metakeb, Mewesson, Metekem Each unit of Metakeb, Mewesson and Metekem requires the following amounts of time in minumtes in each of the indicated departments.
Machining dep't
Inspection dep't
(in minutes)
(in minutes)
(in minutes)
Metakeb
1200
2400
600
Mewesson
1800
1200
3000
Metekem
3000
Assembly dep't
2400
1200
Suppose the total time available per month in machining, assembly and inspection departments are 1050, 1160 and 830 hours respectively.
Required:
Determine the number of units of each product to be produced in a month to use up all the available resources (use Gaussaian method)
Answers
The company should produce 235 units of Metakeb, 96 units of Mewesson, and 17 units of Metekem per month to use up all the available resources.
What is the Gaussian method?
The Gaussian method, also known as Gaussian elimination or row reduction, is a technique for solving systems of linear equations. It involves performing a sequence of operations on the rows of a matrix to transform it into an equivalent matrix that is in row echelon form or reduced row echelon form.
To use the Gaussian method, we need to set up a system of linear equations based on the given information. Let x, y, and z be the number of units of Metakeb, Mewesson, and Metekem produced per month, respectively. Then we have:
Machining department: 1200x + 1800y + 3000z = 1050(60)
Inspection department: 2400x + 1200y = 1160(60)
Assembly department: 600x + 3000y = 830(60)
Simplifying these equations, we get:
Machining department: 20x + 30y + 50z = 3150
Inspection department: 8x + 4y = 232
Assembly department: x + 5y = 139
Now we can use the Gaussian method to solve for x, y, and z:
Step 1: Write the augmented matrix:
| 20 30 50 | 3150 |
| 8 4 0 | 232 |
| 1 5 0 | 139 |
Step 2: Use row operations to get the matrix in row echelon form:
R2 → R2 - 4/5 R3
R1 → R1 - 20R3
| 0 -2 50 | 850 |
| 0 2 -4 | -28 |
| 1 5 0 | 139 |
R2→ -1/2 R2
R1 → R1 + R2
| 0 1 -25 | 407 |
| 0 1 -2 | 14 |
| 1 5 0 | 139 |
R1→ R1 - R2
| 0 0 -23 | 393 |
| 0 1 -2 | 14 |
| 1 5 0 | 139 |
R3→ R3 - 5R2
| 0 0 -23 | 393 |
| 0 1 -2 | 14 |
| 1 0 10 | 65 |
R1→ -1/23 R1
| 0 0 1 | -17 |
| 0 1 -2 | 14 |
| 1 0 10 | 65 |
R2 → R2 + 2R3
| 0 0 1 | -17 |
| 0 1 0 | 96 |
| 1 0 10 | 65 |
R3 → R3 - 10R1
| 0 0 1 | -17 |
| 0 1 0 | 96 |
| 1 0 0 | 235 |
Step 3: Read off the solution from the row echelon form:
z = -17
y = 96
x = 235
Therefore, the company should produce 235 units of Metakeb, 96 units of Mewesson, and 17 units of Metekem per month to use up all the available resources.
To know more about the gaussian method visit:
brainly.com/question/28537650
#SPJ1
A loan is being paid off by payments of 1,000, 2,000, ..., 10,000 at the end of years 1, 2, ..., 10.
The effective annual interest rate is 18%.
Determine the amount of interest in the 7th payment.
Answers
Therefore, the interest portion of the seventh payment is:7,000 x (1 + r + r2 + r3 + r4 + r5 + r6) / r7 - 7,000.
We have the following payments and their corresponding times of payment:At the end of year 1: $1,000At the end of year 2: $2,000At the end of year 3: $3,000At the end of year 4: $4,000At the end of year 5: $5,000At the end of year 6: $6,000At the end of year 7: $7,000
At the end of year 8: $8,000At the end of year 9: $9,000At the end of year 10: $10,000The present value of these payments is:PMT x [(1 - (1 + r)-n) / r]where PMT is the payment, r is the interest rate per year, and n is the number of years till payment.
For the first payment (end of year 1), the present value is:1,000 x [(1 - (1 + r)-1) / r]which equals
1,000 x (1 - 1 / (1 + r)) / r = 1,000 x ((1 + r - 1) / r) = 1,000
For the second payment (end of year 2), the present value is:2,000 x [(1 - (1 + r)-2) / r]which equals 2,000 x (1 - 1 / (1 + r)2) / r = 2,000 x ((1 + r - 1 / (1 + r)2) / r) = 2,000 x (1 + r) / r2
For the seventh payment (end of year 7), the present value is:
7,000 x [(1 - (1 + r)-7) / r]
which equals
7,000 x (1 - 1 / (1 + r)7) / r = 7,000 x ((1 + r - 1 / (1 + r)7) / r) = 7,000 x (1 + r + r2 + r3 + r4 + r5 + r6) / r7
For such more question on corresponding
https://brainly.com/question/11853802
#SPJ8
During summer vacation, Alexa read, on average, 10 pages per night. Now that she has returned to school, she is averaging 80% fewer. How many pages per night is Alexa averaging now?
Answers
During summer vacation, Alexa read, on average, 10 pages per night. The number of pages per night Alexa averaging now is 2 pages.
What is the percentage?A % is a quantity or ratio that, in mathematics, represents a portion of one hundred. A dimensionless relationship between two numbers can be represented in a variety of ways, such as through ratios, fractions, and decimals.
By calculating the percentage of the original Wesley is now reading, we can make the inquiry a little simpler. He is reading 20% of what he used to read rather than 80% less, for example.
Now we need to set up a proportion to solve the problem.
20% of the 10
20/100 = x/10
Cross multiply
20 x 10 = 200
200/100 = 2
He is currently reading 2 pages per night
Thus, the number of pages is 2.
Learn more about percentages, here:
https://brainly.com/question/23442343
#SPJ1
HELPPP PLEASE!!!!!!!!!

Answers
B) 340.34cm3

Last year, the cost of a family-sized dinner at a picnic was $8.50. This year, the cost is $11.56. What is the percent of increase of the price? ( I need a step-by-step explanation not just the answer) ill give brainliest
Answers
price increase = $11.56 - $8.50 = $3.06
percentage increase = $3.06/$11.56 x 100%
= 26.47% (or 26.5%)
hope the explanation was able to help!!
A fancy restaurant put dishes of butter at each table. They divided 4/5 of a kilogram of butter evenly to put 1/5 of a kilogram in each dish. How many butter dishes did they fill?
Answers
Answer: 4
This problem requires basic division. If the restaurant divided 4/5 kg of butter with 1/5 kg on each dish, you would need to compute 4/5 divided by 1/5.
4/5 ÷ 1/5
Using the "KFC" method, or Keep, Change, Flip, you would keep the first number (in this case, 4/5), change the division sign, and flip the fraction to 5/1, or 5. We now have this:
4/5 x 5
To compute this equation, you must multiply the numerators of both of the numbers together. In this case, you would compute (4x5)/5, resulting with 20/5, or 4.
You can check this answer by re-multiplying the numbers together. 1/5 kg of butter per dish, multiplied by the total amount of dishes, 4, you would result in the original 4/5 kg of butter.
Hope this helps!
solve the equation by using the quadratic formula. x^2+2x=6
Answers
Answer:
\(\Huge \boxed{{x=-1\pm \sqrt{7}}}\)
Step-by-step explanation:
x² + 2x = 6
Subtract both sides by 6.
x² + 2x - 6 = 0
ax²+bx+c=0
a=1, b=2, and c=-6
We can apply the quadratic formula.
\(\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
Plug in the values.
\(\displaystyle x=\frac{-2\pm\sqrt{2^2-4(1)(-6)}}{2(1)}\)
Evaluate.
\(\displaystyle x=\frac{-2\pm\sqrt{4-(-24)}}{2}\)
\(\displaystyle x=\frac{-2\pm\sqrt{28}}{2}\)
\(\displaystyle x=\frac{-2\pm 2\sqrt{7}}{2}=-1 \pm \sqrt{7}\)
Answer: Edmentum and Plato
Step-by-step explanation:

Find the volume of the cone shown as a decimal rounded to the nearest tenth.

Answers
Answer:
a. 392.7 yd³Step-by-step explanation:
volume = 1/3 π r² h
where h = 15 yd.
r = 5 yd.
plugin values into the equation:
volume = 1/3 π r² h
= 1/3 * π * 5² * 15
= 392.7 yd³
Answer:
A. 392•8yd^3
Step-by-step explanation:
V= 1/3hπr^21/3×15×22/7×5×58250/21= 392•8yd^3There are 110 students on the team. 100% of them will be off for break. How many students are on break?
Answers
Answer:
110
Step-by-step explanation:
100% of 110 means all of 110, which is just 110.
Are you sure you didn't make a typo here because I'm pretty sure this wouldn't be given on a homework. Just wondering.
What is the probability of drawing to green cards if the first card is replaced before the second draw assume the first card drawn is a green
Answers
If we assume that the first card drawn is green and it is replaced before the second draw, then the probability of drawing two green cards in a row is 12/51, or approximately 0.235.
If we assume that the first card drawn is green and it is replaced before the second draw, then we can say that each draw is independent of the other, and the probability of drawing a green card on each draw is the same.
Let's assume that the deck of cards contains 52 cards, with 13 green cards. Since we know that the first card drawn is green, there are now 51 cards left in the deck, with 12 green cards.
The probability of drawing a green card on the second draw is 12/51, since there are 12 green cards left in the deck out of a total of 51 cards.
To find the probability of drawing two green cards in a row, we need to multiply the probability of drawing a green card on the first draw (which we assumed to be 1 since we know the first card is green) by the probability of drawing a green card on the second draw:
P(drawing two green cards) = 1 x 12/51
Simplifying this expression, we get:
P(drawing two green cards) = 12/51
Therefore, the probability of drawing two green cards is approximately 0.235.
To learn more about card drawn please click on below link
https://brainly.com/question/30505132
#SPJ1
What is the quotient of 4 and 2 over 3Division sign 2 over 3?
Answers
Answer:
9 1/3
Step-by-step explanation:
4 2/3 ÷ 2/3
=14/3 ÷ 2/4
=14/3 · 4/2
=28/3
=9 1/3
Indicated measure for circle o

Answers
Answer:
number a should be half of 82 which is 41
for question b is two times 26 which is 52
the largest orange in a bag has the circumference of 9 5/8 inches. The smallest orange has a circumference
of 7 13/16 inches. Write the difference of the circumferences of the smallest orange and the largest orange
Answers
Answer:
1.81 inches
Step-by-step explanation:
Given that,
The circumference of the largest orange in a bag is \(9\dfrac{5}{8}\ \text{inches}\) and that of smallest orange is \(7\dfrac{13}{16}\ \text{inches}\).
Difference = largest orange - smallest orange
= \(9\dfrac{5}{8}-7\dfrac{13}{16}\\\\=\dfrac{77}{8}-\dfrac{125}{16}\\\\=\dfrac{29}{16}\\\\=1.81\ \text{inches}\)
So, difference of the circumferences of the smallest orange and the largest orange is 1.81 inches
Two different types of injection-molding machines are used to form plastic parts. Two random samples, each of size 300, are selected. 15 defective parts are found in the sample from machine 1 and 8 defective parts are found in the sample from machine 2. Is it reasonable to assume that both machines have the same defective rate
Answers
Answer:
No it is not since there is 15 defectice parts in 2machines and there is 8 broken parts in the one machine
Hope This Helps!!!
Mrs.Robertson sells online math and reading games. His revenue for each game (in dollars) is modeled by the given equations, where x is the number of days since the games went on sale.
Math Game: M(d)=2x^2+8x+2
Reading Game: R(d)=3x+5
Solve the system algebraically. After how many days is the revenue for each game the same? Show your work and explain your answer.
Graph this system to show the solutions. Label each axis appropriately.
Answers
Answer:
Step-by-step explanation:
The reading game equation is 3x + 5. That means that every day the game is for sale he will make $3. The math game is parabolic and doesn't have a slope for which to make the same statement about the amount of money made per day. Where they intersect is where the revenue for each will be the same. On the x axis we have the number of days and on the y axis we have the number of dollars. Solving them algebraically:
\(2x^2+8x+2=3x+5\) and get everything on one side and set it equal to 0:
\(2x^2+5x-3=0\) and factor that however you have learned to factor that quadratic to get:
x = 1/2, -3
The x value indicates the number of days that it would take for the revenue for the games to be the same. Since time can never be negative, we discount the value of -3 and say that it would take 1/2 of a day for the revenue for the games to be the same. As far as the graph goes, I attached a pic below. The red line is the reading game graph and the blue line is the math game parabola. We only need the first quadrant when we graph something like this because, again, days can never be negative so quadrant 2 and 3 are out where x is negative; likewise, the number of dollars will never be negative either, so quadrants 3 and 4 are out. Where those 2 graphs intersect is the number of days that the revenues are the same.

Use Stokes´ Theorem to evaluate ∬s.curl F•nds. Assume that the Surface S is oriented upward.
F= (6yz)i+(5x)j+ (yz(e^(x^2)))k. ; S that portion of the paraboloid z=(1/4)x^2+y^2 for 0≤z≤4
Answers
The surface integral in terms of ρ and θ ∫∫S.((6y - 5)e^(x^2))
To evaluate ∬s.curl F•nds using Stokes' Theorem, we first need to find the curl of the vector field F and then compute the surface integral over the given surface S.
Given vector field F = (6yz)i + (5x)j + (yz(e^(x^2)))k, let's find its curl:
∇ × F = ∂/∂x (yz(e^(x^2))) - ∂/∂y (5x) + ∂/∂z (6yz)
Taking the partial derivatives, we get:
∇ × F = (0 - 0) i + (0 - 0) j + (6y - 5)e^(x^2)
Now, let's parametrize the surface S, which is the portion of the paraboloid z = (1/4)x^2 + y^2 for 0 ≤ z ≤ 4. We can use cylindrical coordinates for this parametrization:
r(θ, ρ) = ρcos(θ)i + ρsin(θ)j + ((1/4)(ρcos(θ))^2 + (ρsin(θ))^2)k
where 0 ≤ θ ≤ 2π and 0 ≤ ρ ≤ 2.
Next, we need to find the normal vector n to the surface S. Since S is oriented upward, the normal vector points in the positive z-direction. We can normalize this vector to have unit length:
n = (∂r/∂θ) × (∂r/∂ρ)
Calculating the partial derivatives and taking the cross product, we have:
∂r/∂θ = -ρsin(θ)i + ρcos(θ)j
∂r/∂ρ = cos(θ)i + sin(θ)j + (1/2)(ρcos(θ))k
∂r/∂θ × ∂r/∂ρ = (-ρsin(θ)i + ρcos(θ)j) × (cos(θ)i + sin(θ)j + (1/2)(ρcos(θ))k)
Expanding the cross product, we get:
∂r/∂θ × ∂r/∂ρ = (ρcos(θ)(1/2)(ρcos(θ)) - (1/2)(ρcos(θ))(-ρsin(θ)))i
+ ((1/2)(ρcos(θ))sin(θ) - ρsin(θ)(1/2)(ρcos(θ)))j
+ (-ρsin(θ)cos(θ) + ρsin(θ)cos(θ))k
Simplifying further:
∂r/∂θ × ∂r/∂ρ = ρ^2cos(θ)i + ρ^2sin(θ)j
Now, we can calculate the surface integral using Stokes' Theorem:
∬s.curl F•nds = ∮c.F•dr
= ∫∫S.((∇ × F)•n) dS
Substituting the values we obtained earlier:
∫∫S.((∇ × F)•n) dS = ∫∫S.((6y - 5)e^(x^2))•(ρ^2cos(θ)i + ρ^2sin(θ)j) dS
We can now rewrite the surface integral in terms of ρ and θ:
∫∫S.((6y - 5)e^(x^2))
for such more question on surface integral
https://brainly.com/question/20771646
#SPJ8
Explain and given an example for each of the logarithmic properties listed below:1. Product rule2. Quotient rule3. Power rule
Answers
Given:
Logarithmic properties:
Find: Product rule, Quotient rule, Power rule.
Sol:.
(1)
Product rule:
\(\log (m\times n)=\log m+\log n\)(2)
Quotient rule:
\(\log (\frac{m}{n})=\log m-\log n\)(3)
Power rule:
\(\log (m^n)=n\log m\)Philip ran 438 miles yesterday. Michael ran 158 miles yesterday.
How much farther did Philip run than Michael?
A. 338 miles
B. 212 miles
C. 314 miles
D. 234 miles
Answers
Step-by-step explanation:
Distance ran by Philip=438 miles
Distance ran by Michael=158 miles
Distance Philip run farther than Michael=(Distance ran by Philip-Distance ran by Michael)
438 miles-138miles
=280miles
Hope it helps you
The weights (in pounds) of 15 preschool children are42, 46, 31, 45, 49, 37, 47, 25, 50, 30, 48, 43, 35, 39, 29Send data to calculatorFind 10th and 75th percentiles for these weights.(If necessary, consult a list of formulas.)(a)(b)The 10th percentile: 9 poundsThe 75th percentile: pounds

Answers
ANSWER:
The 10th percentile: 27.4 pounds
The 75th percentile: 47 pounds
EXPLANATION:
Given:
42, 46, 31, 45, 49, 37, 47, 25, 50, 30, 48, 43, 35, 39, 29
To find:
The 10th and 75th percentiles
Step-by-step solution:
Step 1: Arrange the data in ascending order
25, 29, 30, 31, 35, 37, 39, 42, 43, 45, 46, 47, 48, 49, 50
Step 2: Use the percentile rank formula to determine the 10th percentile;
\(Percentile\text{ }rank=\frac{p}{100}(n+1)\)where;
p = the percentile
n = total number of items in the data set
where p = 10 and n = 15, we'll have;
\(\begin{gathered} Percentile\text{ }rank=\frac{10}{100}(15+1) \\ \\ =\frac{1}{10}(16) \\ \\ =1.6 \end{gathered}\)Since the rank is not an integer, we'll go ahead and use the interpolation method as seen below;
\(\begin{gathered} 1.6-1=0.6 \\ \\ 10th\text{ percentile}=25+0.6(29-25) \\ \\ =25+0.6(4) \\ \\ =25+2.4 \\ \\ =27.4 \end{gathered}\)Therefore, the 10th percentile is 27.4 pounds
Where p = 75 and n = 15, we'll have;
\(\begin{gathered} Percentile\text{ }rank=\frac{75}{100}(15+1) \\ \\ =\frac{75}{100}(16) \\ \\ =12 \end{gathered}\)Since the rank is an integer, we can see that the 75th percentile is 47 pounds
sherry and chris live in different cities. they are planning to meet in nashville, but each will need to drive several days to grt there. they have each calculated the distance in kilometers. sherry uses an equation ans chris uses a table to convert the distance sherry plans to drive each day. the equation and part of the table are shown.
Answers
Answer:
i need to see the table lol do you have a pic?
Step-by-step explanation: