Ten is less than or equal to the difference of a number and negative 4:
Four times the sum of a number and 5 is at least 48:
Answers
Answer:
n - (-4) ≥ 10
4(n+5) ≥ 48
Step-by-step explanation:
n - (-4) ≥ 10
n + 4 ≥ 10
n ≥ 6
4(n+5) ≥ 48
4n + 20 ≥ 48
4n ≥ 28
n ≥ 7
Related Questions
Consider a hash table of size 6. Place the keys 31, 32, and 19 in this table using chaining. Draw the evolution of the hash table for each key placement
Answers
In a hash table of size 6 with chaining, the keys 31, 32, and 19 will be placed in the table as follows:
Key 31: The hash value of 31 will be calculated using a hash function, which will generate a value between 0 and 5. Let's assume that the hash function generates a value of 1 for key 31. The value 31 will be placed in the linked list at index 1 of the hash table.
Key 32: The hash value of 32 will be calculated using the same hash function, which may generate a value different from 1. Let's assume that the hash function generates a value of 3 for key 32. The value 32 will be placed in the linked list at index 3 of the hash table.
Key 19: The hash value of 19 will be calculated using the same hash function, which may generate a value different from 1 and 3. Let's assume that the hash function generates a value of 0 for key 19. The value 19 will be placed in the linked list at index 0 of the hash table.
The evolution of the hash table for each key placement can be illustrated as follows:
Initially, the hash table is empty:
| | | | | | |
After placing key 31 in index 1:
| |31| | | | |
After placing key 32 in index 3:
| |31| |32| | |
After placing key 19 in index 0:
|19|31| |32| | |
As you can see, the values are placed in the linked lists at the respective indices of the hash table. This allows for efficient retrieval of values based on their keys, as the hash table can quickly locate the linked list where the value is stored.
To learn more about hash function : brainly.com/question/31579763
#SPJ11
When Crossett Corporation was organized in January Year 1, it immediately issued 5,200 shares of $50 par, 6 percent, cumulative preferred stock and 9,500 shares of $14 par common stock. Its earnings history is as follows: Year 1, net loss of $13,500; Year 2, net income of $64,700; Year 3, net income of $93,600. The corporation did not pay a dividend in Year 1.
Assume that the board of directors declares a $42,700 cash dividend at the end of Year 2 (remember that the Year 1 and Year 2 preferred dividends are due). How will the dividend be divided between the preferred and common stockholders? (Amounts to be deducted should be indicated with minus sign. Do not round your intermediate calculations.)
Amount Distributed to Shareholders
Preferred Common
Total dividend declared $42,700 0 0
Year 1 Arrearage $15,600 0
Year 2 Preferred dividends 15,600 0
Available for common 42,700
Distributed to common 0 $11,500
Total distribution $31,200 $11,500
Answers
Preferred stockholders will receive $31,200 and common stockholders will receive $11,500 from the $42,700 cash dividend declared at the end of Year 2.
Crossett Corporation issued 5,200 shares of $50 par, 6 percent cumulative preferred stock, and 9,500 shares of $14 par common stock when it was organized in January Year 1. In Year 1, the company experienced a net loss of $13,500 and did not pay a dividend. At the end of Year 2, after a net income of $64,700, the board of directors declared a cash dividend of $42,700.
Preferred stockholders are entitled to receive their dividends first, including any unpaid dividends from previous years. In Year 1, the preferred stockholders were entitled to a dividend of $15,600 (5,200 shares x $50 x 6%), which remained unpaid. In Year 2, they are again entitled to $15,600.
The total amount due to preferred stockholders is $31,200 ($15,600 for Year 1 arrearage + $15,600 for Year 2 preferred dividends). Since the total dividend declared is $42,700, the remaining $11,500 ($42,700 - $31,200) will be distributed to the common stockholders.
You can learn more about stockholders at: brainly.com/question/16225453
#SPJ11
factor the following expression 5x^5-3x^2-10x^3+6
Answers
Answer:hope this helps
Step-by-step explanation:
(x^2 - 2) (5 x^3 - 3)
(x (5 x^2 - 10) - 3) x^2 + 6
Polynomial discriminant:
Δ = -1772976600
Derivative:
d/dx(5 x^5 - 3 x^2 - 10 x^3 + 6) = x (25 x^3 - 30 x - 6)
Indefinite integral:
integral(6 - 3 x^2 - 10 x^3 + 5 x^5) dx = (5 x^6)/6 - (5 x^4)/2 - x^3 + 6 x + constant
Given g(x)=-x+3g(x)=−x+3, find g(1)
Answers
Answer:
g(1) = 2
Step-by-step explanation:
g(x)=−x+3
g(1)=
Let x = 1
g(1) = -1+3 = 2
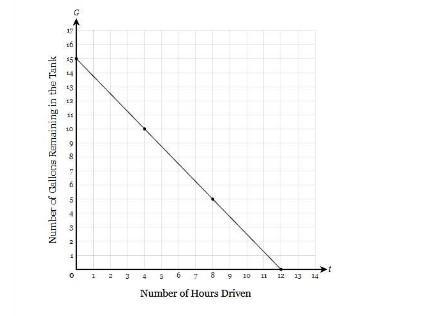
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
Please help me with question 4 thank you !!

Answers
Answer:
The answer is B
Step-by-step explanation:
Got it right
Use the theorems given in this section to answer the following: (a) Let S be a subset of an n-dimensional vector space V. Suppose S contains less than n vectors. Explain why S cannot span V. (b) What is the smallest possible nullity for a 4 x 7 matrix? What is the largest possible rank? Explain. (c) What is the smallest possible nullity for a 7 x 4 matrix? What is the largest possible rank? Explain.
Answers
(a) Let S be a subset of an n-dimensional vector space V. Suppose S contains less than n vectors. Then, the maximum number of linearly independent vectors in S is also less than n. Therefore, the dimension of the span of S is less than n, and hence, S cannot span V.
(b) The nullity of a matrix is the dimension of its null space, which is the set of all solutions to the homogeneous equation Ax = 0, where A is the matrix. The smallest possible nullity for a 4 x 7 matrix is 3, since the nullity cannot be greater than the minimum of the number of rows and columns. The largest possible rank is 4, since the rank cannot be greater than the number of rows.
(c) The smallest possible nullity for a 7 x 4 matrix is also 3, since the nullity cannot be greater than the minimum of the number of rows and columns. The largest possible rank is 4, since the rank cannot be greater than the number of columns. This follows from the rank-nullity theorem, which states that the rank plus the nullity of a matrix equals its number of columns.
To know more about matrix here
https://brainly.com/question/1279486
#SPJ4
Consider the following function f(x)=x4+3, x>=0.Find an explicit formula for f^-1
Answers
The explicit formula for f^-1 is (x-3)^(1/4) and this is obtained by switching the roles of x and y and solving for y in terms of x.
To find the inverse function of f(x)=x^4+3, we need to switch the roles of x and y, and solve for y.
Let y = x^4+3
Subtract 3 from both sides to get:
y - 3 = x^4
Take the fourth root of both sides to isolate x:
(x^4)^(1/4) = (y-3)^(1/4)
Simplify:
x = (y-3)^(1/4)
So the inverse function of f(x) is:
f^-1 (x) = (x-3)^(1/4)
This is the explicit formula for the inverse function of f(x).
To know more about explicit formula visit:
https://brainly.com/question/18069156
#SPJ11
smallest number to be subtracted from 32 to make it a perfect cube
Answers
Answer:
2
Step-by-step explanation:
Answer:
2 is the smallest number
suppose the number of calls received at a call center follows a poisson distribution. suppose the average time between calls received at a call center is 2 minutes. what is the probability that the waiting time until the next call is more than three minutes
Answers
So the probability that the waiting time until the next call is more than three minutes is approximately 0.223.
The Poisson distribution is a probability distribution that describes the number of events occurring in a fixed interval of time or space, given that these events occur independently and at a constant rate.
In this case, we are dealing with the number of calls received at a call center, and we are told that the average time between calls is 2 minutes.
If the number of calls follows a Poisson distribution, we can use the Poisson probability formula to calculate the probability of getting a certain number of calls in a given time period.
However, in this case, we are interested in the waiting time until the next call, which is not directly related to the number of calls. To solve this problem, we can use the fact that the time between two consecutive calls follows an exponential distribution,
which is a continuous probability distribution that describes the time between two events occurring independently and at a constant rate.
The probability density function of the exponential distribution is given by f(x) = λe^(-λx), where λ is the rate parameter (i.e., the reciprocal of the average time between events) and x is the waiting time.
In this case, λ = 1/2 (since the average time between calls is 2 minutes), and we are interested in the probability that the waiting time until the next call is more than three minutes. This can be expressed mathematically as P(X > 3), where X is the waiting time.
To calculate this probability, we can use the cumulative distribution function (CDF) of the exponential distribution, which gives the probability that X is less than or equal to a certain value.
The CDF of the exponential distribution is given by F(x) = 1 - e^(-λx). Therefore, P(X > 3) = 1 - P(X ≤ 3) = 1 - F(3) = 1 - (1 - e^(-1.5)) = e^(-1.5) ≈ 0.223, So the probability that the waiting time until the next call is more than three minutes is approximately 0.223.
This means that there is about a 22.3% chance that the call center will not receive a call for more than three minutes, given that the calls arrive independently and at a constant rate.
To know more about probability click here
brainly.com/question/15124899
#SPJ11
Hello, can u help me out please i will give brainlist :)

Answers
Answer:
$5.75
Step-by-step explanation:
Find the difference between the weeks as this will give you the difference hence the amount deposited each week
0->1
is 12.00->17.75
diffrence is $5.75
1->2
is 17.75->23.50
diffrence is $5.75
the amount saved each week is $5.75
Use the box method to distribute and simplify (5x – 3) (-4x – 5). Drag and drop
the terms to the correct locations of the table.
(5x – 3) (- 4x – 5)
NEED HELEOEO

Answers
Answer:
your answer is below
-20x +15
3. A rocket is launched from a height of 3 meters with an initial velocity of 15 meters per second.
a. Model the situation with a quadratic equation.
b. What is the maximum height of the rocket? When will this occur?
c. What is the height of the rocket after four seconds? What does this mean?
d. When will the rocket hit the ground?
e. At what time will the rocket be 13 meters from the ground?
Answers
Let the rocket is launched at an angle of \theta with respect to the positive direction of the x-axis with an initial velocity u=15m/s.
Let the initial position of the rocked is at the origin of the cartesian coordinate system where the illustrative path of the rochet has been shown in the figure.
As per assumed sine convention, the physical quantities like displacement, velocity, acceleration, have been taken positively in the positive direction of the x and y-axis.
Let the point P(x,y) be the position of the rocket at any time instant t as shown.
Gravitational force is acting downward, so it will not change the horizontal component of the initial velocity, i.e. \(U_x=U cos\theta\) is constant.
So, after time, t, the horizontal component of the position of the rocket is
\(x= U \cos\theta t \;\cdots(i)\)
The vertical component of the velocity will vary as per the equation of laws of motion,
\(s=ut+\frac12at^2\;\cdots(ii)\), where,s, u and a are the displacement, initial velocity, and acceleration of the object in the same direction.
(a) At instant position P(x,y):
The vertical component of the initial velocity is, \(U_y=U sin\theta\).
Vertical displacement =y
So, s=y
Acceleration due to gravity is \(g=9.81 m/s^2\) in the downward direction.
So, \(a=-g=-9.81 m/s^2\) (as per sigh convention)
Now, from equation (ii),
\(y=U sin\theta t +\frac 12 (-9.81)t^2\)
\(\Rightarrow y=U \sin\theta \times \frac {x}{U \cos\theta} +\frac 12 (-g)\times \left(\frac {x}{U \cos\theta} \right)^2\)
\(\Rightarrow y=U^2 \tan\theta-\frac 1 2g U^2 \sec^2 \theta\;\cdots(iii)\)
This is the required, quadratic equation, where \(U=15 m/s\) and \(g=9.81 m/s^2\).
(b) At the highest point the vertical velocity,v, of the rocket becomes zero.
From the law of motion, \(v=u+at\)
\(\Rightarroe 0=U\sin\theta-gt\)
\(\Rightarroe t=\frac{U\sin\theta}{g}\cdots(iv)\)
The rocket will reach the maximum height at \(t= 1.53 \sin\theta s\)
So, from equations (ii) and (iv), the maximum height, \(y_m\) is
\(y_m=U\sin\theta\times \frac{U\sin\theta}{g}-\frac 12 g \left(\frac{U\sin\theta}{g}\right)^2\)
\(\Rightarrow y_m=23 \sin\theta -11.5 \sin^2\theta\)
In the case of vertical launch, \(\theta=90^{\circ}\), and
\(\Rightarrow y_m=11.5 m\) and \(t=1.53 s\).
Height from the ground= 11.5+3=14.5 m.
(c) Height of rocket after t=4 s:
\(y=15 \sin\theta \times 4- \frac 12 (9.81)\times 4^2\)
\(\Rightarrow y=15 \sin\theta-78.48\)
\(\Rightarrow -63.48 m >y> 78.48\)
This is the mathematical position of the graph shown which is below ground but there is the ground at \(y=-3m\), so the rocket will be at the ground at t=4 s.
(d) The position of the ground is, y=-3m.
\(-3=U\sin\theta t-\frac 1 2 g t^2\)
\(\Rightarrow 4.9 t^2-15 \sin\theta t-3=0\)
Solving this for a vertical launch.
\(t=3.25 s\) and \(t=-0.19 s\) (neglecting the negative time)
So, the time to reach the ground is 3.25 s.
(e) Height from the ground is 13m, so, y=13-3=10 m
\(10=U\sin\theta t-\frac 1 2 g t^2\)
Assume vertical launch,
\(4.9 t^2-15 \sin\theta t+10=0\) [using equation (ii)]
\(\Rightarrow t=2.08 s\) and \(t=0.98 s\)
There are two times, one is when the rocket going upward and the other is when coming downward.

NO JOKE 70 POINTS!!!!!!!! I WILL GIVE BRANLIEST AND RATE!!!! MATH EXPERTS COME HELP!!! AT LEAST TAKE A LOOK!!! LIKE WHERE ARE THE GENIUSES!!EASY I AM JUST DUMBREAD THIS AND THEN ANSWER THE QUESTION
READ THIS THEN ANSWER THE QUESTION:
There are so many items for sale in our world! Some of the items you can buy will appreciate in value. This means that as time passes, the value of the item increases. If you decide to sell the item at a later time, you should be able to sell it for more than you paid. Some common examples of items that appreciate in value include houses, stocks, and some types of art.
Other items you can buy will depreciate in value. This means that as time passes, the value of the item decreases. If you decide to sell the item at a later time, you will likely have to sell it for less than you paid for it. Cars, game systems, and jewelry are examples of items that usually depreciate as time passes. The majority of items that depreciate never reach a value of $0. Their worth attains some minimum, positive value that is greater than $0 and then their price stabilizes.
In 1981, IBM manufactured and sold one of the first personal computers. The machine was called the IBM Personal Computer (PC) 5150 and the full model retailed for $3,000. Similar to modern technology, the value of this item depreciated over time. The function that models how the PC 5150 depreciated as time passed is , where x is the number of years after 1981 and f(x) is the value of the PC 5150.
1. Evaluate the depreciation function at f(0). Show your work and use function notation as needed. What does this number represent?
2. Find the vertex of the depreciation function. What does this point represent in context of this problem? Show your work and explain your process.
Answers
Answer:
The quadratic equation is f(x)=20x^{2} -400x +3000.
1. This number represents the amount of money it was sold for.
2. Vertex =(10,1000)
Step-by-step explanation:
This point represents the amount of money the computer was worth at its lowest point.
[just answering so you can give the other guy brainiest]
Joe kept track of how much TV she watched each day for two weeks how many hours did she spend watching TV
Answers
The total hours joe spent watching TV each day for two weeks is 12 1/2 hours
Total hours spent watching TVTotal hours spent watching TV for two weeks = Number of hours × days
= (0 × 1) + (1/4 × 1) + (1/2 × 1) + (3/4 × 3) + (1 × 3) + (1 1/4 × 4) + (1 1/2 × 1)
= 0 + 1/4 + 1/2 + 9/4 + 3 + 5 + 3/2
= 8 + (1+2+9+6) / 4
= 8 + 18/4
= 8 + 4 2/4
= 8 + 4 1/2
= 12 1/2 hours
Learn more about number line:
https://brainly.com/question/24644930
#SPJ1

solve the system:
y = 4x - 19
y = - 3x + 23
Answers
Answer:
( 6 , 5 )
Step-by-step explanation:
Solve for the first variable in one of the equations, then substitute the result into the other equation.

Negative three times the difference of x and y
Answers
will mark brainlist if its right

Answers
Answer: S<\-2
Hope i was some help.
Step-by-step explanation: sorry I can’t put the right sign my keybored won’t let me but you know what it stands for.
3s+6s</-5(s+2)
start off with -5(s+2) you multiply -5 with s and it is -5s then you do the same for +2 take -5 and multiply by +2 pos times a neg is always a neg so it’s -10.
3s+6<\-5s-10
So you have to get rid of the -5s so your going to do the inverse which is add 5 to -5 and it will get rid of -5s but then you have to add 5 to 3s and that will be 8s.
8s+6</-10
Now your going to get rid of the +6 and to do that you do the inverse you subtract 6 and it will get rid of it now you have to do the same for -10 so you will subtract 6 to -10 and that will equal -16.
Now you have to divide!
8s/8 </ -16/8
And it should equal s <\-2
PLS HELP! WILL GIVE BRAINLIST!!!!
The following expression is a polynomial: 3x^2y^2 - 2xy
Part A: Classify the polynomial according to its number of terms. Explain how you know your answer is correct.
Part B: Classify the polynomial according to its degree. Explain how you know your answer is correct
Answers
Answer:
It is a trinomal because there is 3 terms
It is a quadratic because the highest degree is x^2
All in all, It is a Quadratic Trinomal
Step-by-step explanation:
the researcher is interested in determining whether there is evidence that the two processes yield different average errors. the population standard deviations are unknown but are assumed equal. assume that process a is the first population. if we test the null hypothesis at the 1% level of significance, what is the decision?
Answers
The conclusion of the hypothesis is that we fail to reject the null hypothesis and conclude that the means are different.
What is the conclusion of the Hypothesis?Let us first define the hypothesis;
Null Hypothesis; H₀: μ_a = μ_b
Alternative Hypothesis; Hₐ: μ_a ≠ μ_b
From the given significance value, we can say that we will reject H₀ if the calculated test statistic is greater than 2.797 or t is less than 2.797.
The pooled variance from the attached table with the aid of a statistics calculator gives;
Pooled variance = 0.5938
The test statistic from online calculator is; t = -3.299 or 3.299
This test statistic falls falls within the rejection region and so we reject the null hypothesis and conclude that there is a difference in the average errors of the two processes.
Read more about Hypothesis Conclusion at; https://brainly.com/question/15980493
#SPJ1

LEVEL 3! HELP PLEASE!
Write the correct order
of letters to the finish line
С
B
А
Example
ABCGH
Answers
According to the given example, the correct order of letters to the finish line is А, B, C, G, H.
Based on the given example "ABCGH," we can determine the correct order of letters to the finish line. Comparing the given example with the options, we find that the first letter is "A." Moving on, the next letter in the given example is "B," followed by "C."
Therefore, the correct order of the first three letters is "А, B, C." As for the remaining letters, "G" appears after "C" in the given example, and finally "H" is the last letter. Combining all the identified letters, the correct order of letters to the finish line is "А, B, C, G, H."
Learn more about Letters here: brainly.com/question/13943501
#SPJ11
A(-9, 4), b(-7, -2) and c(a, 2) are the vertices of a triangle that is right-angled at b. find the value of a.
Answers
A has a value of 6.875.
We have a right-angled triangle at vertex B. Therefore, its hypotenuse will be the longest side, and it will be opposite the right angle. The hypotenuse will connect the points A and C. As a result, we may use the Pythagorean Theorem to solve for A. The distance between any two points on the coordinate plane may be calculated using the distance formula.
So, we'll use the distance formula to calculate AC and BC, then use the Pythagorean Theorem to solve for a.
AC² = (a + 9)² + (2 - 4)² = (a + 9)² + 4
BC² = (-7 - (a + 9))² + (-2 - 4)² = (-a - 16)² + 36
By the Pythagorean Theorem, a² + 16² + 36 = (a + 16)².
Then:a² + 256 + 36 = a² + 32a + 256
Solve for a on both sides: 220 = 32a
a = 6.875
Therefore, a has a value of 6.875.
Know more about Pythagorean Theorem here,
https://brainly.com/question/14930619
#SPJ11
Find the lowest common denominator for the set of fractions.
\(\frac{7}{x^{2}+4x+4} ,\frac{5}{4-x^{2} }\)
Answers
A regular pentagon and a regular hexagon are both inscribed in the circle below. Which shape has a bigger area? Explain your reasoning.
I don't understand how to find either of their areas, if anyone could walk me through it I would appreciate it.

Answers
The polygon shape that possesses the bigger area from the two given is: Hexagon
How to identify the area of a Polygon?Polygons are defined as closed shapes that are two-dimensional. They possess straight sides and have the same number of sides as they have angles. Polygons have names that relate to how many sides they have.
A hexagon has more sides than a pentagon.
A hexagon is a polygon that has six sides and a pentagon is a polygon that has five sides.
Now, the more sides the polygon has, the more area it covers inside the circle as it will obviously be wider.
Thus, we can infer that the hexagon will have a bigger area.
Read more about Polygon area at: https://brainly.com/question/8409681
#SPJ1
please help me on this question!
* I will give brainlist!

Answers
Answer:
x = 84 m---------------------------
Given similar triangles:
ΔDOT ~ ΔPANWe know that corresponding sides of similar triangles have same ratio.
The ratios are:
DO/PA = DT/PNSubstitute values and solve for x:
24/16 = x/563/2 = x/56x = 56*3/2x = 84Please help me with this! I will give brainlist!

Answers
Answer:
Its the 2nd Dot
Step-by-step explanation:
What is the third angle of a right triangle if one of the angles measures 51.1 degrees
Answers
Answer:
38.9°
Step-by-step explanation:
The three angles in a triangle add up to 180°. Also, a right triangle has a right angle in it. A right angle is 90°.
90° + 51.1° + x = 180°
141.1 + x = 180°
subtract 141.1°
x = 38.9°
A random sample of 9 pins has an mean of 3 inches and variance of .09. Calculate the 99% confidence interval for the population mean length of the pin. Multiple Choice 2.902 to 3.098 2.884 to 3.117 2.864 to 3.136 2.228 to 3.772 2.802 to 3.198
Answers
The 99% confidence interval for the population mean length of the pin is (3 - 0.3355, 3 + 0.3355) approximately equal to 2.864 to 3.136.
The equation for the certainty interim for the populace mean is:
CI = test mean ± t(alpha/2, n-1) * \((test standard deviation/sqrt (n))\)
Where alpha is the level of importance (1 - certainty level), n is the test estimate, and t(alpha/2, n-1) is the t-value for the given alpha level and degrees of opportunity (n-1).
In this case, the test cruel is 3 inches, the test standard deviation is the square root of the fluctuation, which is 0.3 inches, and the test estimate is 9.
We need a 99% certainty interim, so alpha = 0.01 and the degrees of flexibility are 9-1=8. Looking up the t-value for a two-tailed test with alpha/2=0.005 and 8 degrees of opportunity in a t-table gives an esteem of 3.355.
Substituting these values into the equation gives:
CI = 3 ± 3.355 * (0.3 / sqrt(9))
CI = 3 ± 0.3355
So the 99% confidence interval for the population mean length of the pin is (3 - 0.3355, 3 + 0.3355), which simplifies to (2.6645, 3.3355).
The closest choice is 2.864 to 3.136.
learn more about standard deviation
brainly.com/question/23907081
#SPJ4
Lola uses 4 cups of sugar for 3 gallons of lemonade. How many cups of sugar would she need for a
one gallon of lemonade?
Answers
Answer:
4=3
x=1
4=3x
4/3=x
1.3=x
what is the smallest positive integer a such that the intermediate value theorem guarantees a zero exists between 0 and a?
Answers
The smallest positive integer that the intermediate value theorem guarantees a zero exists between 0 and a is 3.
What is the intermediate value theorem?
Intermediate value theorem is theorem about all possible y-value in between two known y-value.
x-intercepts
-x^2 + x + 2 = 0
x^2 - x - 2 = 0
(x + 1)(x - 2) = 0
x = -1, x = 2
y intercepts
f(0) = -x^2 + x + 2
f(0) = -0^2 + 0 + 2
f(0) = 2
(Graph attached)
From the graph we know the smallest positive integer value that the intermediate value theorem guarantees a zero exists between 0 and a is 3
For proof, the zero exists when x = 2 and f(3) = -4 < 0 and f(0) = 2 > 0.
Your question is not complete, but most probably your full questions was
Given the polynomial f(x)=− x 2 +x+2 , what is the smallest positive integer a such that the Intermediate Value Theorem guarantees a zero exists between 0 and a ?
Thus, the smallest positive integer that the intermediate value theorem guarantees a zero exists between 0 and a is 3.
Learn more about intermediate value theorem here:
brainly.com/question/28048895
#SPJ4
