Suppose you invested $1200 for four years. You earned $312 in simple
interest. What is the interest rate?
Answers
Answer: 6.5%
Step-by-step explanation: 312/4 = 78
78/1200 = 0.065
0.065 x 100 = 6.5%
Related Questions
The set of numbers whose decimal representations are neither.
Answers
The set of numbers whose decimal representations are neither repeating nor terminating is known as the set of irrational numbers.
Irrational numbers are numbers that cannot be expressed as fractions and have non-repeating and non-terminating decimal representations. Examples of irrational numbers include √2, π (pi), and e (Euler's number). These numbers are infinite and non-repeating, meaning their decimal representation goes on forever without following a specific pattern. The proof that √2 is irrational was first demonstrated by the ancient Greeks, and the irrationality of π and e was proven much later in history. Irrational numbers play a significant role in mathematics and are essential for understanding concepts like limits, calculus, and geometry.
Learn more about Irrational numbers here
brainly.com/question/29194459
#SPJ11
What is the mathematical term for the set of numbers whose decimal representations are neither terminating (finite decimal) nor repeating (infinite periodic decimal)?
NEED HELP WITH MATH GEOMETRY

Answers
The perimeter of parallelogram ABCD is given as follows:
360 units.
What is the perimeter of a polygon?The perimeter of a polygon is given by the sum of all the lengths of the outer edges of the figure, that is, we must find the length of all the edges of the polygon, and then add these lengths to obtain the perimeter.
On a parallelogram, the opposite sides are congruent, hence the equations relating x and y are given as follows:
9x + 68 = 6y + 14.19x = 5y + 1.The solutions to the system are given as follows:
x = 4 and y = 15.
Hence the side lengths are:
Base: 6y + 14 = 6 x 15 + 14 = 104.Height: 19 x 4 = 76.The perimeter is of:
P = 2 x (76 + 104)
P = 360 units.
More can be learned about the perimeter of a polygon at https://brainly.com/question/3310006
#SPJ1
CAN SOMEONE HELP ME WITH THIS IXL ITS P.7 EIGHTH GRADE!!!!
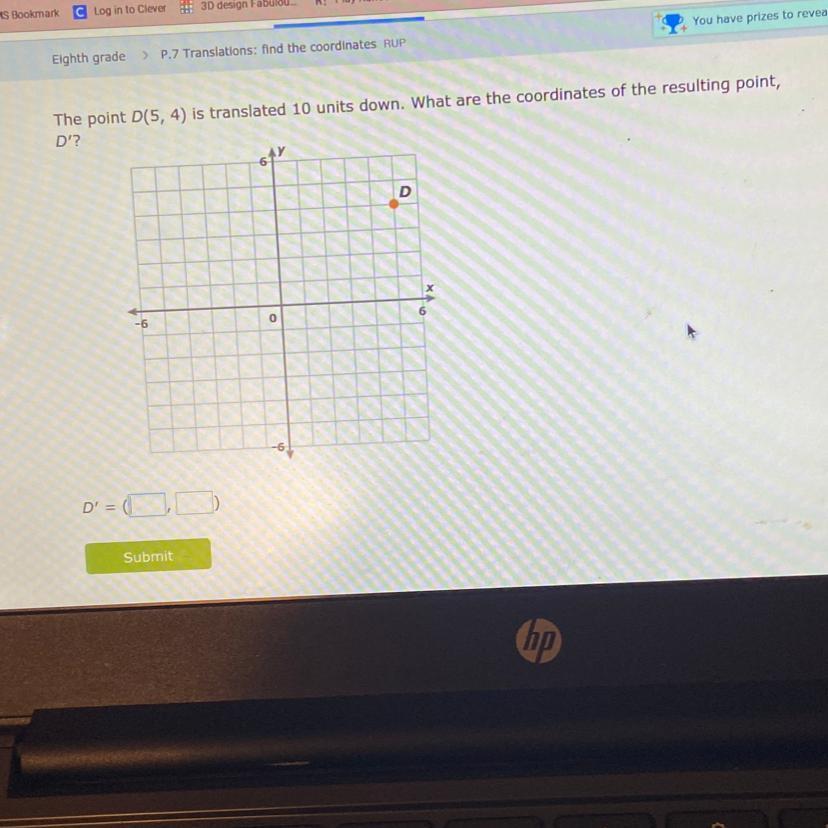
Answers
1/3^3= 1/27 I will need this answer soon as possible plz

Answers
Reduce by cancelling the common factors.
(13)x−1=27 Convert the exponential equation to a logarithmic equation using the logarithm base (13) of the right side (27) equals the exponent (x−1)log13(27)=x−1
write an equation in y=mx+b form for the following data
x y
-2 6
0 5
2 4
6 2
Answers
i’m so confused on this question

Answers
Answer:
l: y = 4
m: y = -2x + 4
n: y = x - 1
p: undefined
Step-by-step explanation:
See attached graph

what is the annual percentage yield (apy) for money invested at the given annual rate? round results to the nearest hundredth of a percent. 3.5% compounded continuously. a. 3.56%. b. 35.5%.c. 35.3%. d. 3.50%
Answers
The correct answer is option c. 35.3%. The annual percentage yield (apy) for money invested at the given annual rate of 3.5% compounded continuously is 35.3%.
The annual percentage yield (APY) is a measure of the total interest earned on an investment over a year, taking into account the effects of compounding.
To calculate the APY for an investment with continuous compounding, we use the formula:
\(APY = 100(e^r - 1)\),
where r is the annual interest rate expressed as a decimal.
In this case, the annual interest rate is 3.5%, which, when expressed as a decimal, is 0.035. Plugging this value into the APY formula, we get:
\(APY = 100(e^{0.035} - 1).\)
Using a calculator, we find that \(e^{0.035\) is approximately 1.03571. Substituting this value back into the APY formula, we get:
APY ≈ 100(1.03571 - 1) ≈ 3.571%.
Rounding this value to the nearest hundredth of a percent, we get 3.57%.
Among the given answer choices, option c. 35.3% is the closest to the calculated value.
Options a, b, and d are significantly different from the correct answer.
Therefore, option c. 35.3% is the most accurate representation of the APY for an investment with a 3.5% annual interest rate compounded continuously.
To learn more about annual percentage yield visit:
brainly.com/question/30774234
#SPJ11
1) A pair of die is tossed. What is the probability that the total is less than 11
2) There are 8 college basketball teams in a certain Sub-Division.
How many different Top 5 Ranking lists are possible?
Answers
The probability that the total is less than 11 when a 1) pair of dice is tossed is 1. 2) The number of permutations of 8 teams taken 5 at a time can be represented as P(8, 5) and can be calculated as 8!/(8-5)! = 8!/3! = (8 * 7 * 6 * 5 * 4)/(5 * 4 * 3 * 2 * 1) = 56.
When two dice are tossed, the maximum possible sum is 12 (when both dice show 6). Since we are interested in the probability that the total is less than 11, it means we are considering all the possible outcomes where the sum of the dice is less than 11.
We can analyze all the possible outcomes:
When the sum is 2, there is only one combination (1 and 1).When the sum is 3, there are two combinations (1 and 2, 2 and 1).When the sum is 4, there are three combinations (1 and 3, 2 and 2, 3 and 1).When the sum is 5, there are four combinations (1 and 4, 2 and 3, 3 and 2, 4 and 1).When the sum is 6, there are five combinations (1 and 5, 2 and 4, 3 and 3, 4 and 2, 5 and 1).When the sum is 7, there are six combinations (1 and 6, 2 and 5, 3 and 4, 4 and 3, 5 and 2, 6 and 1).When the sum is 8, there are five combinations (2 and 6, 3 and 5, 4 and 4, 5 and 3, 6 and 2).When the sum is 9, there are four combinations (3 and 6, 4 and 5, 5 and 4, 6 and 3).When the sum is 10, there are three combinations (4 and 6, 5 and 5, 6 and 4).Summing up all the possible outcomes, we find that there are 36 possible outcomes when tossing a pair of dice. Since all the outcomes have a sum less than 11, the probability of getting a sum less than 11 is 1.
To find the number of different Top 5 Ranking lists possible with 8 college basketball teams, we need to calculate the number of permutations of the teams taken 5 at a time.
This can be done using the formula for permutations: P(n, r) = n!/(n-r)!, where n is the total number of items and r is the number of items being selected.
In this case, we have 8 teams and we want to select 5 teams. So, P(8, 5) = 8!/(8-5)! = 8!/3! = (8 * 7 * 6 * 5 * 4)/(5 * 4 * 3 * 2 * 1) = 56.
Therefore, there are 56 different Top 5 Ranking lists possible.
To know more about probability, refer here:
https://brainly.com/question/31469353#
#SPJ11
I need help it’s a major grade



Answers
Answer:
Look to explanation
Step-by-step explanation:
The question says the original mosaic is surrounded by a 3 inch by 5 inch frame. The length has 5 squares & the width has 3 squares, so that means each square is an inch long.
1. Perimeter is adding up how long all the sides are. So for the original you add 3 + 5 + 3 + 5 = 16 inches
2. Area is length x width, so we multiply 3 x 5 = 15 inches squared
3. Since each square is an inch, to find the length we add up all the squares & we get 10. Then we do the same for the width & get 6. To figure perimeter, we add up all the sides 10 + 6 + 10 + 6 = 32 inches
4. Area is length x width, so 10 x 6 = 60 inches squared
5. For the original we needed 16 inches of steel. For the larger one, we needed 32 inches. 32 inches is 2x bigger than 16.
6. For the original we had an area of 15 inches squared. For the larger one we had 60 inches squared. 60 is 4x bigger than 15.
Analyze the diagram below and complete the instructions that follow.
Find m

Answers
Answer:
D. 70.53
Step-by-step explanation:
To solve this problem, one must use the right angle trigonometric rations. These ratios can be used to describe the ratio between the sides and an angle in a right triangle. Please note, each side is named relative to the angle that one is looking at, thus the same side can acquire different names based on the angle one uses to describe it. The trigonometric ratios are the following:
\(sin(\theta)=\frac{opposite}{hypotenuse}\\\\cos(\theta)=\frac{adjacent}{hypotenuse}\\\\tan(\theta)=\frac{opposite}{adjacent}\)
In this case, one is asked to find the measure of (<CBA), one is given the hypotenuse (the side opposite the right angle), and the side adjacent to this angle. Therefore, one should use the cosine (cos) function to find this angle.
\(cos(\theta)=\frac{adjacent}{hypotenuse}\)
Substitute,
\(cos(CBA) = \frac{3}{9}\)
Simplify
\(cos(CBA) = \frac{1}{3}\)
Inverse operations,
\(CBA=cos^-1(\frac{1}{3})\)
Compute,
m<CBA = 70.53
Factor the polynomial expression 4x2 +9.
Answers
Answer:
Step-by-step explanation:
Factor it by first setting it equal to 0:
\(4x^2+9=0\) Now subtract 9 from both sides:
\(4x^2=-9\) Divide both sides by 4:
\(x^2=-\frac{9}{4}\) Then take the square root of both sides:
x = ±\(\sqrt{-\frac{9}{4} }\) , which of course is not allowed. Therefore, we have to allow for the imaginary numbers in this solution. Knowing that,
x = ±\(\sqrt{-1*\frac{9}{4} }\) is an equivalent radicand, we can now replace -1 with its imaginary counterpart:
x = ±\(\sqrt{i^2*\frac{9}{4} }\)
Each one of the elements in the radicand are perfect squares, so we simplify as follows:
x = ±\(\frac{3}{2}i\)
And there you go!
Solve the following system:
4x+3y=-2 and 6y=-4-8x
Answers
To solve this system, first multiply the first equation by 2 to get 8x+6y=-4.
What is equation?An equation is a mathematical statement that expresses two values or ideas as equal. It consists of two parts: an expression and an equals sign. The expression on the left side of the equals sign is compared to the expression on the right side of the equals sign. An equation may be used to describe relationships between physical, chemical, and mathematical quantities.
Then add the two equations to get 14x=-8. Therefore,
x=-8/14 and substituting x=-8/14
into the first equation yields y=3/2.
Thus, the solution to the system is x=-8/14 and y=3/2.
To know more about Equation click-
https://brainly.com/question/2972832
#SPJ1
if john gives allen 5 dollars and allen gives frank 2 dollars, the 3 boys will have the same amount of money. how much more money does john have than allen
Answers
Answer:
0$ or 3$
Step-by-step explanation:
If you are saying right now, then the answer would be zero. But, when we start, we can make and equation. Let's use J as John, A as Allen, and F and Frank. They all have n amount of money. Now, we work backwards: If A didn't give F 2$, then F now has n-2 and A has n+2. If J didn't give A 5$, then J would have n+5 and A would have n+2-5=n-3. The difference between those two is 8. Therefore, John has 8$ more.
13. Zahra likes to go rock climbing with her friends. In the past, Zahra has climbed to the top of the
wall 7 times in 28 attempts. Determine the odds against Zahra climbing to the top.
A. 3:1
B. 4:1
C. 3:11
D. 3:4
Answers
Answer:
the odds against Zahra climbing to the top are,
B. 4:1
Step-by-step explanation:
Since she has climbed 7 times in 28 attempts,
the probability of a successful climb is,
P = 7/28
P = 1/4
So, the odds against Zahra climbing to the top are 4:1
For this right triangle drawn on the coordinate plane what calculation could be used to find the length of a C?

Answers
Answer:
AB^2 + BC^2 = AC^2
Step-by-step explanation:
the pythagorean theorem( a^2 + b^2 = c^2) is used to solve for the hypotenuse which in this case is AC
^2 means squared incase you didnt know
hope this helped!
Determine the interval of convergence I and radius of convergence for the following series: (-1) n=1 -(x-2) ngh The interval of convergence is and the radius of convergence is R
Answers
The interval of convergence is (-1, 3) and the radius of convergence is R = 1.
To determine the interval of convergence and radius of convergence for the given series \((-1)^n=1 * (x-2)^n,\) we need to use the ratio test.
The ratio test states that if we take the limit of the absolute value of the ratio of the n+1th term and the nth term as n approaches infinity, and the limit is less than 1, then the series converges absolutely. If the limit is greater than 1, the series diverges, and if the limit is equal to 1, then the test is inconclusive.
Applying the ratio test to the given series, we have:
\(|((-1)^n+1 * (x-2)^(n+1))/((-1)^n * (x-2)^n)|= |(-1)*(x-2)|= |x-2|\)
Taking the limit as n approaches infinity, we have:
lim (|x-2|) = |x-2|
Since the limit is less than 1 for |x-2| < 1, the series converges absolutely.
To find the radius of convergence, we need to find the value of x for which the limit is exactly 1.
lim (|x-2|) = 1
|x-2| = 1
x - 2 = 1 or x - 2 = -1
x = 3 or x = 1
Therefore, the interval of convergence is (-1, 3) and the radius of convergence is R = 1.
for more questions on convergence
https://brainly.com/question/3402595
#SPJ11
Find the difference between (1.3 × 108) and (3.8 × 107). write the final answer in scientific notation. −2.5 × 101 2.5 × 10−1 9.2 × 107 9.2 × 108
Answers
Answer: i need help on the same question
Step-by-step explanation:
please
A researcher wants to set up a regression equation where Y is a function X. Evaluate the researcher’s options given the following scenarios: (3)
i. Y is I(0); X is I(0)
ii. Y is I(2); X is I(0)
iii. Y is I(1); X is I(1); and the error term is I(0).
Answers
The appropriate regression model depends on the stationarity properties of both the dependent and independent variables, as well as the error term. The researcher can use a standard OLS regression model with first-order differencing of both Y and X.
In the first scenario, both Y and X are I(0), which means they are stationary time series. In this case, the researcher can perform a standard linear regression analysis, as the stationary series would lead to a stable long-run relationship. The answer from this model will be reliable and less likely to suffer from spurious regressions. In the second scenario, Y is I(2) and X is I(0). This implies that Y is integrated of order 2 and X is stationary. In this case, the researcher should first difference Y twice to make it stationary before performing a regression analysis. However, this approach might not be ideal as the integration orders differ, which can lead to biased results.
In the third scenario, Y and X are both I(1) and the error term is I(0). This indicates that both Y and X are non-stationary time series, but their combination might be stationary. The researcher should employ a co-integration analysis, such as the Engle-Granger method or Johansen test, to identify if there is a stable long-run relationship between Y and X. If co-integration is found, then an error correction model can be used for more accurate predictions.
To know more about regression visit:-
https://brainly.com/question/28168620
#SPJ11
The coefficient of variation is a better measure of risk than the standard deviation if the expected returns of the securities being compared differ significantly.
A. True
B. False
Answers
True. The coefficient of variation is a better measure of risk than the standard deviation if the expected returns of the securities being compared differ significantly.
The coefficient of variation (CV) is a relative measure of risk that takes into account the standard deviation and the mean of a distribution. It is a better measure of risk than the standard deviation when comparing securities with significantly different expected returns because it adjusts for the differences in the means.
The CV is calculated as the ratio of the standard deviation to the mean, and it allows for the comparison of the risk of investments with different expected returns on a standardized basis. Therefore, it is a useful tool for investors who want to compare the risk of investments that have different levels of expected returns. However, it should be noted that the CV has limitations and should not be the sole measure of risk used in investment analysis.
For more questions like Variation visit the link below:
https://brainly.com/question/14095452
#SPJ11
A rectangular garden will be fenced using 400 feet of fencing material. One side of the garden is partly covered by the barn and that part will not be fenced. If the barn is 50 feet long, what are the dimensions that will maximize the area of the garden? what is the largest possible area?.
Answers
The dimension of the max garden is 125*125 and the max area is 15625 square feet.
Let the length and width of the garden be L and B.
Now, let the barn is along the width. So, now the width became = B-50
So the perimeter = 2(L+B-50)
Now to fence the garden we need 400 feet material.
So, 2(L+B-50) = 400
L+B-50 = 200
B = 250-L .........(i)
So the area of the total garden is given by,
A = LB = L(250-L) \(=250L-L^2\)
So now differentiating the area with respect to length,
dA/dL = 250-2L
\(\frac{d^2A}{dL^2}=\) -2
Now, dA/dL = 0 gives,
250-2L = 0
2L = 250
L= 125
At L = 125, \(\frac{d^2A}{dL^2}=-2 < 0\)
Max A = \(250\times125-125^2=15625\) square feet
So area is maximum when L = 125 feet.
Then the width = B = 250-125 = 125 feet.
Hence the dimension of the max garden is 125*125 and the max area is 15625 square feet.
To know more about Dimension refer to:
https://brainly.com/question/26740257
#SPJ4
helppppp please !!!!

Answers
Explanation:
25300(0.85) ^7 =
81110.60033…
help me out? :)
don't guess, if u dont know just dont answer. NO LINKS.

Answers
Answer:
A cube
Step-by-step explanation:
If you fold it, you'll see
NEED HELP IN NEED THE ANSWER BY TO NIGHT PLE.
A deli sells small, medium, and large sack lunches. Each bottle of water costs $1, and each apple costs $1. Each sandwich costs s dollars. Some customers buy sack lunches, and some customers buy items separately.
Amy buys 8 sandwiches and 12 waters. Her total cost is 8s + 12.
Bob buys 8 small sack lunches. These sack lunches include 1 sandwich, 1 water, and 1 apple. His total cost is 8(s + 2).
Cathy buys 4 medium sack lunches. These sack lunches do not include water. Her total cost is 4(2s + 3).
Part C
Dave buys 5 sandwiches for $31.25. Write an expression that can be used to find the cost of x sandwiches. Show your work or explain your answer.
Fill in the missing values in this table.
Part D
How much did Amy pay? How much did Bob pay? How much did Cathy pay? Show your work or explain your answer.

Answers
Answer:
Step-by-step explanation:
1 sandwich is 6.25 (because 31.25/5)
2 sandwiches is 12.5
3 sandwiches are 18.75
4 sandwiches are 25
5 sandwiches are 31.25
6 sandwiches are 37.5
Amy - 8s + 12
8(6.25) +12 = 62
Amy paid $62.
Bob - 8(s + 2)
8(6.25 + 2) = 66
Bob pays $66.
Cathy - 4(2s + 3)
4(2 x 6.25 + 3) = 62
Cathy paid $62.
Determine the value for x in the equation x over 5 and 7 tenths equals 2 and 3 tenths.
Answers
Answer: i believe your answer is 21x=100
Step-by-step explanation: hope this helps
How many paths are there from $A$ to $B,$ if you travel along the edges? You can travel along each edge at most once, but you can pass through the same point more than once. (You can pass through $B,$ as long as you end up at the point $B.$) [asy] unitsize(1.5 cm); draw((0,0)--dir(60)--(1,0)); draw((0,0)--(1,0)); draw((0,0)--dir(-60)--(1,0)); label("$A$", (0,0), W); label("$B$", (1,0), E); [/asy]
Answers
Answer:
There are $\boxed{3}$ paths from $A$ to $B.$
WILL GIVE BRAINLIEST AND THANKS. find the value of x
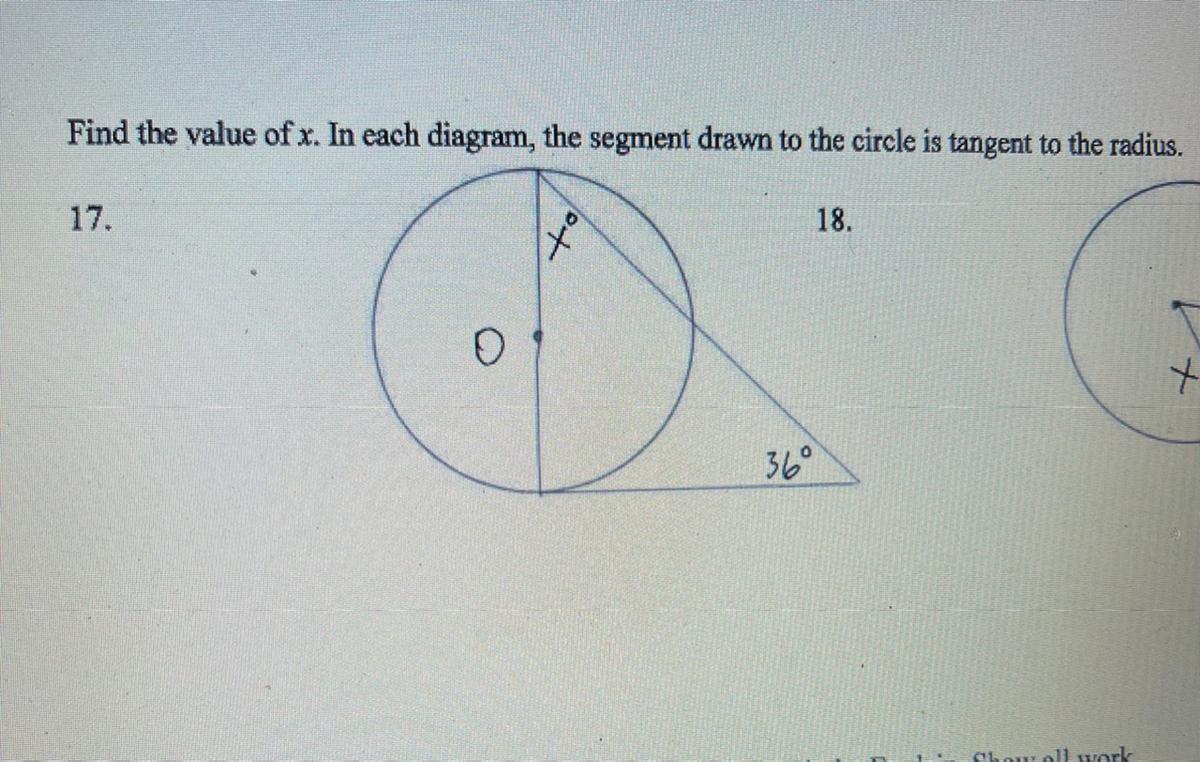
Answers
Answer:
180 - 36? I dont exactly remember how to do this
Step-by-step explanation:
Sorry if its not right
Find the minimum value of the function f(x) = 0.8x2 + 11.2x + 42 to the
nearest hundredth.
Answers
Answer:
The minimum value is 2.8. The vertex is (-7, 2.8).
Step-by-step explanation:
Through the x^2 term we identify this as a quadratic function whose graph opens up. The minimum value of this function occurs at the vertex (h, k). The x-coordinate of the vertex is
-b 11.2
x = --------- which here is x = - ------------ = -7
2a 2(0.8)
We need to calculate the y value of this function at x = -7. This y-value will be the desired minimum value of the function.
Substituting -7 for x in the function f(x) = 0.8x^2 + 11.2x + 42 yields
f(-7) = 0.8(-7)^2 + 11.2(-7) + 42 = 2.8
The minimum value is 2.8. The vertex is (-7, 2.8).
a is subset of b. b must include everything a has and at least one additional element. how many ways can a and b have subsets?
Answers
The number of ways that A and B can have subsets is the product of the number of subsets of A and the number of subsets of B, or (2^n) * (2^m) = 2^(n+m).
Subset Ways CalculationA set is a collection of distinct objects, and a subset is a set that contains only elements that are also in another set. If set A is a subset of set B, then all elements of A are also elements of B.
The number of subsets of a set with n elements is 2^n. So, if set A has n elements and set B has m elements (where m > n), the number of subsets of A is 2^n and the number of subsets of B is 2^m. The number of ways that A and B can have subsets is the product of the number of subsets of A and the number of subsets of B, or (2^n) * (2^m) = 2^(n+m).
Learn more about Subset Ways Calculation here:
https://brainly.com/question/13391651
#SPJ4
calculate the distance travelled by the object in the diagram. 27 meter northwest 27 meters 405 meters northwest 21 meters 20 meters northwest next
Answers
The object traveled a total distance of 500 meters.
To calculate the total distance traveled by the object, we can add up the individual distances traveled in each direction.
The distances traveled in each direction are as follows:
- 27 meters northwest
- 27 meters
- 405 meters northwest
- 21 meters
- 20 meters northwest
To calculate the total distance traveled, we add these distances together:
27 + 27 + 405 + 21 + 20 = 500 meters
Therefore, the object traveled a total distance of 500 meters.
To know more about total distance, refer here:
https://brainly.com/question/19339844
#SPJ4
work out the total surface area of the pyramid

Answers
The total surface area of the pyramid is 335 square centimeters
How to determine the total surface areaThe formula for determining the total surface area of a pyramid is expressed as;
TSI = 1/2(PI) + B
Given that;
TSI is the total surface area of the pyramidP is the base perimeter of the pyramidI is the slant height of the pyramidB is the base area of the pyramidNow, let's determine the base perimeter
Perimeter = 2( l + w)
Substitute the values
Perimeter = 2 ( 8 + 12)
Perimeter = 40 centimeters
The base area is given as;
Base area = 8(12)
Base area = 96 square centimeters
Substitute the values, we have;
Total surface area = 1/ 2 (40)(12) + 96
Total surface area = 240 + 96
Total surface area = 335 square centimeters
Hence, the value is 335 square centimeters
Learn more about total surface area here:
https://brainly.com/question/26638955
#SPJ1