Suppose that has a uniform distribution on the interval
[−2,2]. Find Cov(,^2). Show whether or not these random
variables are independent.
Answers
The covariance between the random variables X and Y is calculated as Cov(X, Y) = (1/32) * (∫(x^2√y) dy) - (x^2/32) * √y. Since the covariance is not zero, X and Y are not independent.
To find the covariance of two random variables, we need to know their joint probability distribution. In this case, the random variable has a uniform distribution on the interval [-2, 2]. Let's denote it as X. The random variable Y is defined as the square of X, i.e., Y = X^2.
To find the covariance, we first need to find the marginal probability distributions of X and Y. Since X is uniformly distributed on the interval [-2, 2], its probability density function (pdf) is constant within that interval and zero outside. Therefore, the pdf of X is:
fX(x) = 1/4, for -2 ≤ x ≤ 2
= 0, otherwise
To find the marginal pdf of Y, we can use the transformation method. Since Y = X^2, we can write X = √Y. Taking the derivative of this transformation, we have dX/dY = 1/(2√Y). Therefore, the pdf of Y can be obtained as:
fY(y) = fX(√y) * |dX/dY|
= (1/4) * (1/(2√y))
= 1/(8√y), for 0 ≤ y ≤ 4
= 0, otherwise
Now, we can calculate the covariance using the formula:
Cov(X, Y) = E(XY) - E(X)E(Y)
To find E(XY), we need to calculate the integral of XY * fX,Y(x, y) over the joint distribution. Since X and Y are independent, their joint distribution is simply the product of their marginal distributions:
fX,Y(x, y) = fX(x) * fY(y) = (1/4) * (1/(8√y))
E(XY) = ∫∫xy * fX,Y(x, y) dx dy
= ∫∫xy * (1/4) * (1/(8√y)) dx dy
= (1/32) * ∫∫xy * (1/√y) dx dy
= (1/32) * ∫(∫xy * (1/√y) dx) dy
Now we integrate with respect to x:
∫xy * (1/√y) dx = (1/√y) * (x^2/2) = (x^2/(2√y))
Now we integrate this expression with respect to y:
∫(x^2/(2√y)) dy = x^2√y
Therefore, E(XY) = (1/32) * ∫(x^2√y) dy
Now we can calculate E(X):
E(X) = ∫x * fX(x) dx
= ∫x * (1/4) dx
= (1/4) * (x^2/2)
= x^2/8
And E(Y):
E(Y) = ∫y * fY(y) dy
= ∫y * (1/(8√y)) dy
= (1/8) * ∫y^(-1/2) dy
= (1/8) * (2√y)
= √y/4
Finally, we can calculate the covariance:
Cov(X, Y) = E(XY) - E(X)E(Y)
= (1/32) * ∫(x^2√y) dy - (x^2/8) *
(√y/4)
= (1/32) * (∫x^2√y dy) - (x^2/32) * √y
To determine if X and Y are independent, we can check if the covariance is zero. If Cov(X, Y) = 0, then X and Y are independent. However, since the covariance expression is not zero, X and Y are not independent in this case.
To learn more about covariance click here: brainly.com/question/17137919
#SPJ11
Related Questions
The quadratic f(x) = x^2 + 6x + 6 is shifted to g (x) = (x - 2)^2 + 3. ALGEBRAICALLY
determine;
a) The vertex of both quadratics
b) The axis of symmetry of both quadratics
C)
The transformation made from f(x) to g(x)
d)
Write the equation of a transformation of up 2 and left 3 from g(x)
Answers
Plot the following points on the coordinate plane. Connect them, and find the area of the shape that results.
(3,2) (-6,2) (-6,-8) (3,-8)
Answers
Answer:
The shape is a square and it's area is 121
HOPE THIS HELPS!!!
Someone help me with this
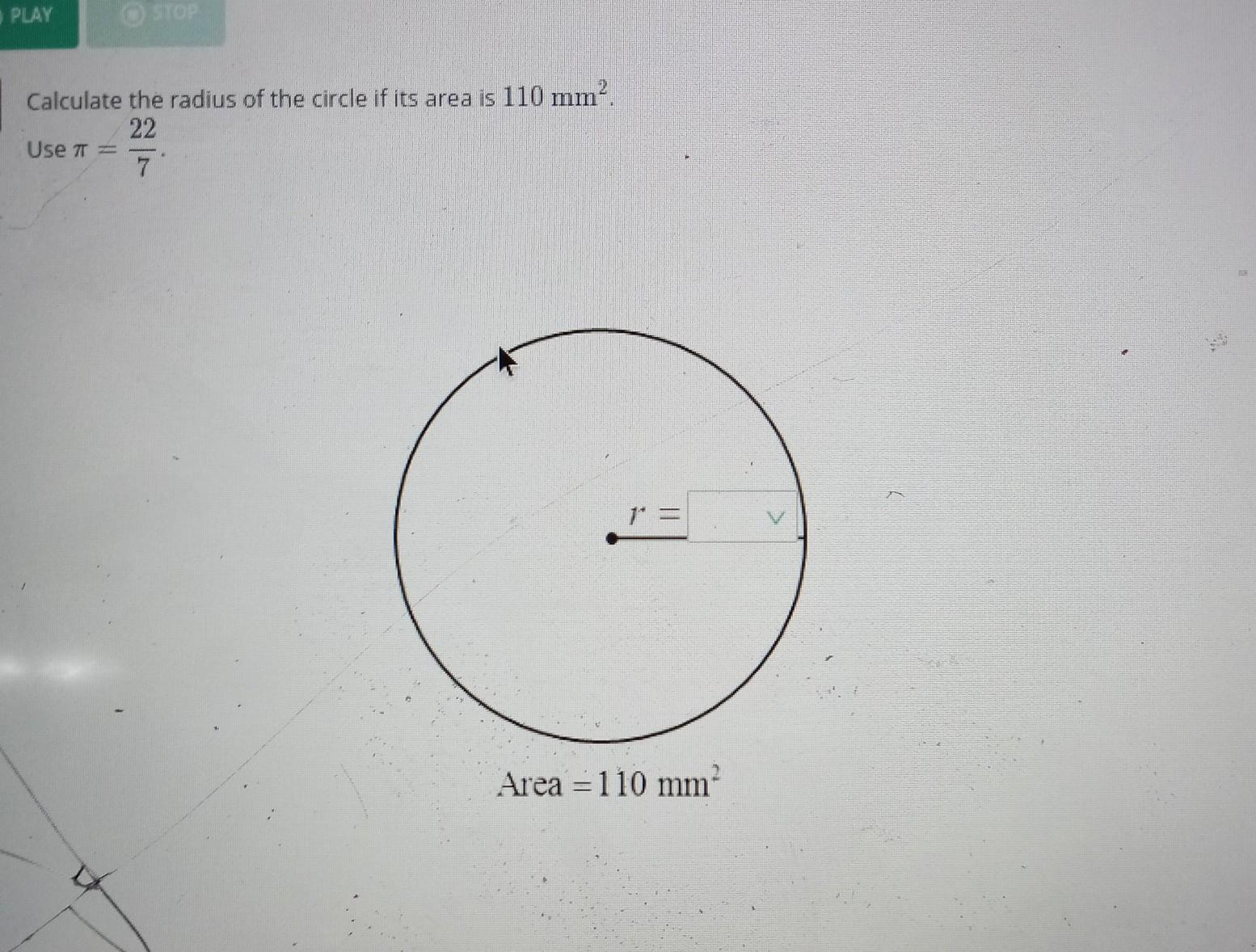
Answers
Answer:
radius = √35 mm or 5.916 mm
Explanation:
\(\sf area \ of \ circle = \pi r^2\)Here:
area of circle: 110 mm²π taken as 22/7Solve for radius:
\(\rightarrow \sf \pi r^2 = 110\)
\(\rightarrow \sf \dfrac{22}{7} r^2 = 110\)
\(\rightarrow \sf r^2 = \dfrac{110(7)}{22} =35\)
\(\rightarrow \sf r = \sqrt{35}\)
Let's see
Area=110πr²=11022/7r²=110r²≈110(7)/22r²=770/22r=√770/22r=5.9mmThe correlation coefficient for blood pressure and amount of vegetables eaten in a group of people is −0.7. Analyze the following statement:
High blood pressure is caused by not eating vegetables.
Is this a reasonable conclusion?
Answers
Answer:
Yes, that is a reasonable conclusion
Step-by-step explanation:
Answer:
This is not a reasonable conclusion.
Step-by-step explanation:
Even though there is a strong negative correlation, not eating vegetables doesn't necessarily cause high blood pressure.
Good luck, hope this helps you out! (◕‿◕✿)
Jackson and Ginger are both learning to ride a bike. Jackson can travel y = 4. 1 miles, and Ginger travels y = 3x + 15.
When will the distance traveled in miles (y) and the minutes spent biking (x) be the same for both friends?
Answers
The solution for x is approximately -3.63. To find the point at which the distance traveled (y) and the time spent biking (x) are the same for both friends,
we need to set their respective equations equal to each other and solve for x.
For Jackson:
y = 4.1 miles
For Ginger:
y = 3x + 15 miles
Setting these equations equal to each other:
4.1 = 3x + 15
Now, let's solve for x:
3x = 4.1 - 15
3x = -10.9
x = -10.9 / 3
x ≈ -3.63
The solution for x is approximately -3.63. However, in the context of time spent biking, it doesn't make sense to have a negative value.
Therefore, we can conclude that there is no point at which the distance traveled and the time spent biking are the same for both friends based on the given information.
learn more about equation here: brainly.com/question/29657983
#SPJ11
an independent group of food service personnel conducted a survey on tipping practices in a large metropolitan area. they collected information on the percentage of the bill left as a tip for 2525 randomly selected bills. the average tip was 13.1.1% of the bill with a standard deviation of 2.6%2.6%. assume that the tips are approximately normally distributed. construct an interval to estimate the true average tip (as a percent of the bill) with 90% confidence. round the endpoints to two decimal places, if necessary.
Answers
90% confidence interval is 11.65 <µ< 114.566 as per standard deviation data.
What is a standard deviation?
The term "standard deviation" (or "") refers to a measurement of the data's dispersion from the mean. When the standard deviation is low, the data are concentrated around the mean, and when it is large, the data are widely dispersed.Sample mean (T) = 13.11%
Sample standard deviation (s) = 2.6
Sample size (h) = 25
significance level = α = 1 -0.90 = 0.1
Degrees of freedom for t- distribution (df) = 24
Critical value = ta/2
df = \(t_{0.1}\), df=24 = ±2.80
The margin of error (E) =\(t_\frac{a}{2} , df\frac{s}{\sqrt{h} }\)
E=2.8X \(\frac{2.6}{\sqrt{25} }\) =1.456
Limits of 90%. Confidence Interval is.
Lowest limit = X' - E = 13.11-1.456 = 11.65
Upper limit= X' + E = 13.11+1.456 = 14.566
90% confidence interval is 11.65 <µ< 114.566 as per standard deviation data.
Learn more about standard deviation here:
https://brainly.com/question/24298037
#SPJ4
Suppose that the financial ratios of a potential borrowing firm took the following values:
X1 = 0.30
X2 = 0
X3 = -0.30
X4 = 0.15
X5 = 2.1
Altman's discriminant function takes the form:
Z = 1.2 X1+ 1.4 X2 + 3.3 X3 + 0.6 X4 + 1.0 X5
The Z score for the firm would be
A. 1.64.
B. 1.56.
C. 2.1.
D. 3.54.
E. 2.96
Answers
The Z score for the firm would be B. 1.56.
To calculate the Z score for the potential borrowing firm using Altman's discriminant function, we'll need to substitute the given values of X1, X2, X3, X4, and X5 into the formula:
Z = 1.2 X1 + 1.4 X2 + 3.3 X3 + 0.6 X4 + 1.0 X5
By plugging in the values:
Z = 1.2(0.30) + 1.4(0) + 3.3(-0.30) + 0.6(0.15) + 1.0(2.1)
Now, perform the calculations:
Z = 0.36 + 0 - 0.99 + 0.09 + 2.1
Then, add the resulting numbers:
Z = 1.56
Altman's Z score is a widely-used financial tool that helps to predict the likelihood of a company going bankrupt. A Z score below 1.8 typically indicates a higher risk of bankruptcy, while a score above 3 suggests a lower risk. In this case, the firm's Z score of 1.56 suggests that it may be at a higher risk of bankruptcy, and further analysis should be conducted to determine the company's financial stability before extending credit or making an investment.
Therefore, the correct option is B.
Know more about Altman's discriminant function here:
https://brainly.com/question/22223063
#SPJ11
What is the value of the t score for a 99% confidence interval if we take a sample of size 20?
A. 2.845
B. 2.861
C. 3.552
D. 3.579
Answers
Answer:
2.861
Step-by-step explanation:
What is the value of the t score for a 99% confidence interval if we take a sample of size20? Thus, the t-score for a 99% confidence interval for sample size 20 is 2.861.
A 36-inch board is to be cut into three pieces so that the second piece is 3 times as long as the first piece and the third piece is 5 times as long as the first piece. If x represents the length of the first piece, find the lengths of all three pieces.
Answers
The measure of the length of first piece is 4 units, the length of second piece is 12 units and the length of third piece is 20 units.
What is an equation?In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign =.
Given that, a 36-inch board is to be cut into three pieces.
Let x represents the length of the first piece.
The second piece is 3 times as long as the first piece and the third piece is 5 times as long as the first piece.
Now, the length of the second piece is 3x
The length of the third piece is 5x
So, total length = x+3x+5x
9x=36
x=4 units
So, 3x=12 units and 5x=20 units
Therefore, the measure of the length of first piece is 4 units, the length of second piece is 12 units and the length of third piece is 20 units.
To learn more about an equation visit:
https://brainly.com/question/14686792.
#SPJ9
PLEASE ANSWER ASAP
A farmer is going to divide her 30 acre farm between two crops. Seed for crop A costs $30 per acre. Seed for crop B costs $15 per acre. The farmer can spend at most $600 on seed.
If crop B brings in a profit of $90 per acre and crop A brings in a profit of $160 per acre, how many acres of each crop should the farmer plant to maximize her profit?
Answers
Answer:
Rearrange Inequalities
0<= A <=40
0<= B <= 40
A <= -B + 40
A <= -2B + 50
Acres:: A + B <= 40
Seed:: 10A + 20B <= 500
Profit function:: P = 110A + 40B
Step-by-step explanation:

Answer:
the farmer should plant 40 acres of crop B.
Step-by-step explanation:
The restriction equations are:
x + y = 40 acres (1) (for areas; x = the area for crop A; y = the area for crop B).
10x + 20y = 700 (2) for the seed cost
or
x + 2y = 70
We have the following system of equations:
x + y = 40
x + 2y = 70
The additional obvious restrictions are x >= 0 and y >= 0.
The objective function is the profit:
F(x, y) = 60x + 70y
According to the conception/ideology of the linear programming method, we need to evaluate the
objective function F(x, y) = 60x + 70y in three points (corner points):
(0, 40), (35, 0) and (10, 30)
We need to find the point where the objective function is maximal:
F(0, 40) = 60*0 + 70*40 = $2,800
F(35, 0) = 60*35 + 70*0 = $2,100
F(10, 30) = 60*10 + 70*30 = $2,700
Follows, the farmer should plant 40 acres of crop B.
If the pattern below follows the rule "starting with 10, every consecutive line has a number 1 less than the previous line," how many marbles must be in the seventh line?

Answers
Answer: B: 4
Step-by-step explanation: just took the test
The seventh line will be having 4 marbles which can be determined by taking the given data as an arithmetic progression with the first term as 1 and the common difference -1. Hence, option B is the right choice.
What is an Arithmetic Progression?An arithmetic progression (A.P.) is a series where every term is the sum of the previous term and a common difference.
The first term of an arithmetic progression is denoted by a, and its common difference is denoted by d. The n-th term of an arithmetic progression can be found using the formula
n-th term = a + (n-1)d.
How do we solve the given question?We are given a pattern, starting with 10 marbles and every consecutive line has 1 less marble than the previous line. We are asked to find the number of marbles in the 7th line.
This can be seen as an arithmetic progression with the first term a = 10, and the common difference d = -1.
We are asked to find the number of marbles in the 7th line. This can be taken as the 7th term of the given arithmetic progression.
n-th term = a + (n-1)d
or, 7th term = 10 + (7-1)(-1) = 10 + 6(-1) = 10 - 6 = 4.
∴ The seventh line will be having 4 marbles which can be determined by taking the given data as an arithmetic progression with the first term as 1 and the common difference -1. Hence, option B is the right choice.
Learn more about an arithmetic progression at
https://brainly.com/question/6561461
#SPJ2
Please help me out with this problem, and an explanation would also be helpful. I was out of class for a couple days last week so I don’t really know what I’m doing. Thanks in advance

Answers
The missing length s in the triangle is 64736.
We are given that;
The triangle with shaded region area= 952yd2
Now,
By substituting the values in the area formula;
952=1/2 * s * h
952=1/2 * s * 34
s= 952 * 34 * 2
s= 64736
Therefore, by area the answer will be 64736.
Learn more about area here:
https://brainly.com/question/4887838
#SPJ1
Find the perimeter of this figure?

Answers
Answer:
22 in.
Step-by-step explanation:
7+4+7+4 = 14+8 = 22
An artist draws a square chalk mural with side length a. The artist decides to enlarge the mural. The area of the new mural is represented by (5a)(3a + 2).
Simplify the expression (5a)(3a + 2).
8a + 2
15a2 + 10a
15a2 + 10
8a2 + 10a
Answers
The expression (5a)(3a + 2) simplifies to 15a^2 + 10a. This is obtained by multiplying 5a with both terms inside the parentheses using the distributive property. The final result cannot be further simplified. So, Option B is correct. Option B.
To simplify the given expression, (5a)(3a + 2), we apply the distributive property to distribute the factor 5a to both terms inside the parentheses. This involves multiplying 5a by each term separately.
First, we multiply 5a by 3a. Multiplying these two terms gives us 15a^2, where the coefficient 15 comes from multiplying 5 by 3 and the variable a is squared due to the multiplication of two a's.
Next, we multiply 5a by 2. This multiplication results in 10a, where the coefficient 10 comes from multiplying 5 by 2, and the variable a remains unchanged.
Combining the two simplified terms, we have 15a^2 + 10a. This expression cannot be further simplified because there are no like terms to combine.
The term 15a^2 represents the enlarged area of the mural, obtained by multiplying the lengths of the sides of the original square mural (side length a) by the factor 5 and squaring the variable a. The term 10a represents an additional area added during the enlargement process, obtained by multiplying the side length a by the factor 2.
In conclusion, the simplified form of (5a)(3a + 2) is 15a^2 + 10a. So OptioN B is correct.
For more question on simplifies visit:
https://brainly.com/question/723406
#SPJ8
What the answer to this

Answers
Answer:
(2 x + 5) (x - 1) (x + 7) thus the answer is D.)
Step-by-step explanation:
Factor the following:
2 x^3 + 17 x^2 + 16 x - 35
The possible rational roots of 2 x^3 + 17 x^2 + 16 x - 35 are x = ± 1/2, x = ± 5/2, x = ± 7/2, x = ± 35/2, x = ± 1, x = ± 5, x = ± 7, x = ± 35. Of these, x = -5/2, x = 1 and x = -7 are roots. This gives 2 x + 5, x - 1 and x + 7 as all factors:
Answer: (2 x + 5) (x - 1) (x + 7)
A football team earns 6 points for a touchdown and 3 points for a field goal. In one game, a team scored a touchdown and some field goals. The total points the team scored is 18 points. Write an equation using the variable fthat can be used to find the number of field goals the team scored.
Enter the correct answer in the box.
Answers
Answer:
Step-by-step explanation:
6+3(f)=18
6+3f=18
3f=12
f=4
write a function in terms of $t$ that represents the situation. your starting annual salary of $35,000 increases by 4% each year.
Answers
In this problem, the starting annual salary is $35,000 and increases by 4% each year. The task is to write a function in terms of t that represents this situation.
Modeling salary growth over time is a common task in finance and economics.
Let's call the salary after t years s(t).
Then, the salary after t years can be represented by the following function: s(t) = 35,000 * (1 + 0.04t).
This function says that the starting salary of $35,000 is multiplied by (1 + 0.04t) to find the salary after t years.
The constant 0.04 represents the 4% increase each year.
For example, if t = 1, then the salary after 1 year would be $35,000 * (1 + 0.04 * 1) = $36,400, and if t = 2, then the salary after 2 years would be $35,000 * (1 + 0.04 * 2) = $37,888.
Learn more about function here brainly.com/question/12431044
#SPJ4
who knows how to solve this problem

Answers
a = 3√3
a = 3 × 1.732
a = 5.196
a = 5.2 inches
evaluate the circulation of g⃗ =xyi⃗ zj⃗ 2yk⃗ around a square of side 6 , centered at the origin, lying in the yz-plane, and oriented counterclockwise when viewed from the positive x-axis.
Answers
The circulation of the vector field G around the given square in the yz-plane is i * [(18 + 12k) * 6], where k represents an unspecified constant.
To evaluate the circulation of the vector field G = xyi + zj + 2yk* around the given square, we can use Stokes' theorem.
Stokes' theorem states that the circulation of a vector field around a closed curve is equal to the surface integral of the curl of the vector field over any surface bounded by the curve.
In this case, the square is lying in the yz-plane and has a side length of 6, centered at the origin. The square is oriented counterclockwise when viewed from the positive x-axis.
The surface bounded by the square in the yz-plane is a rectangle with sides of length 6 and 6.
The curl of the vector field G is given by:
curl(G) = (∂Q/∂y - ∂P/∂z)i + (∂R/∂z - ∂P/∂x)j + (∂P/∂y - ∂R/∂x)kwhere P = xy, Q = 0, and R = 2y.
Taking the partial derivatives, we have:
∂P/∂x = y
∂P/∂y = x
∂P/∂z = 0
∂Q/∂x = 0
∂Q/∂y = 0
∂Q/∂z = 0
∂R/∂x = 0
∂R/∂y = 2
∂R/∂z = 0
Therefore, the curl of G simplifies to:
curl(G) = xi + 2kj
Now, we need to calculate the surface integral of curl(G) over the rectangular surface bounded by the square.
The surface integral is given by:
∬S curl(G) · dS
Since the surface is a rectangle lying in the yz-plane, the normal vector of the surface is in the x-direction, i.e., n = i.
The magnitude of the normal vector is |n| = 1.
The surface integral simplifies to:
∬S curl(G) · dS = ∬S (curl(G) · n) dS
Since the normal vector is constant and equal to i, we can pull it out of the integral:
∬S curl(G) · dS = i ∬S (curl(G)) dS
The rectangular surface has dimensions 6 x 6, so the area of the surface is 36 square units.
Now, evaluating the surface integral:
∬S curl(G) · dS = i ∬S (xi + 2kj) dS = i ∬S (x + 2k) dS
Integrating over the rectangular surface:
∬S curl(G) · dS = i ∫(0 to 6) ∫(0 to 6) (x + 2k) dx dy
Integrating with respect to x:
∬S curl(G) · dS = i ∫(0 to 6) [(x^2/2 + 2kx)] (0 to 6) dy
= i ∫(0 to 6) (18 + 12k) dy
= i [(18 + 12k) * 6]
Therefore, the circulation of G around the given square is i * [(18 + 12k) * 6]
To learn more about vector fields visit : https://brainly.com/question/17177764
#SPJ11
PLEASE HELP ME! I know its pretty simple but like... yee

Answers
Answer:
b i think
Step-by-step explanation:
the sign would flip if you divide by a negative number
Explanation: The sign changes because you’re dividing both sides by a negative number! Sorry if this is wrong!
-8x2(x+8)=8(2+6) how do i solve this and 4n+3/2=2n-5/1?
Answers
1) \(-8x^2\left(x+8\right)=8\left(2+6\right)\)
\(-8x^3-64x^2=64\)
\(-8x^3-64x^2-64=64-64\)
\(-8x^3-64x^2-64=0\)
\(-8x^2+0.97035\dots x-7.88051\dots \approx \:0\)
\(x\approx \:-8.12129\dots\)
2) \(4n+\frac{3}{2}=2n-\frac{5}{1}\)
\(4n+\frac{3}{2}=2n-5\)
\(4n+\frac{3}{2}-\frac{3}{2}=2n-5-\frac{3}{2}\)
\(4n=2n-\frac{13}{2}\)
\(4n-2n=2n-\frac{13}{2}-2n\)
\(2n=-\frac{13}{2}\)
\(\frac{2n}{2}=\frac{-\frac{13}{2}}{2}\)
\(n=-\frac{13}{4}\)
Please help me with this question. I’m stuck

Answers
Answer:
should be 17
Step-by-step explanation:
find what x is by setting the equations equal to each other. (x=8) Just plug 8 into the equation to get the answer: 17
what is the answer to this promblem

Answers
9514 1404 393
Answer:
to eliminate x: multiply the first by 3, and the second by -4to eliminate y: multiply the first by 2, and the second by 5Step-by-step explanation:
Pick the variable you want to eliminate. Determine the coefficients of that variable in the two equations. Negate one of them. Multiply each equation by the coefficient that came from the other equation.
__
To eliminate x
The x-coefficients are 4 and 3. If we negate 4, then the resulting y-coefficient will be positive. We choose to multiply the first equation by 3, the second by -4.
Here is the result of adding those:
3(4x +5y) -4(3x -2y) = 3(7) -4(-12) ⇒ 23y = 69
To eliminate y
The y-coefficients are 5 and -2. If we negate -2, then the resulting x-coefficient will be positive. We choose to multiply the first equation by 2 and the second by 5.
Here is the result of adding those:
2(4x +5y) +5(3x -2y) = 2(7) +5(-12) ⇒ 23x = -46
Answer:
Step-by-step explanation:
to kill x: duplicate the primary by 3, and the moment by -4 to eliminate y: increase the primary by 2, and the moment by 5 Step-by-step explanation: Pick the variable you need to eliminate. Decide the coefficients of that variable within the two conditions. Refute one of them. Increase each condition by the coefficient that came from the other equation. __ To dispense with x The x-coefficients are 4 and 3. On the off chance that we invalidate 4, then the coming about y-coefficient will be positive. We select to increase the primary condition by 3, the moment by -4. Here is the result of including those: 3(4x +5y) -4(3x -2y) = 3(7) -4(-12) ⇒ 23y = 69 To dispose of y The y-coefficients are 5 and -2. If we nullify -2, at that point the coming about x-coefficient will be positive. We select to duplicate the primary condition by 2 and the moment by 5. Here is the result of including those: 2(4x +5y) +5(3x -2y) = 2(7) +5(-12) ⇒ 23x = -46
hope this helps
I don’t want link or down I will give Brinley’s answer to quick explanation

Answers
Answer:
5 power points
Step-by-step explanation:
The graph shows the unit measurement as 5 power points for one goblin so that is the correct answer.
Which of the following is true about the relation shown here: {(2,5),(−1,3),(1,−7),(−4,5),(−5,0)}
Answers
Can you help me with 3 answers please



Answers
The area of the attached quadrilaterals are
area of rhombus = 20 square units
area of rectangle = 60 square units
none of the above
How to find the area of the images attachedThe formula for area of rhombus is
Area = base × height
Area = 5 × 4
= 20 square units
The formula for area of rectangle is
Area = length × width
Area = 10 × 6
= 60 square units
The formula for area is
Area = base × height
Area = 7 × 4
= 28 square units
Learn more about area at
https://brainly.com/question/25292087
#SPJ1
How do you find the x for this ?

Answers
So since all sides are congruent, all the angles should be equal as well. This means that if you divide 180 by 3 (number of angles) you should get 60. You then set the equation equal to 60 and solve:
2x^2-140=60
2x^2=200
x^2=100
x=10
PLEASE HELP!?!?!?!?! In our amusement park that we built this week, the ride Diablo’s Domain had revenue of $250,000,000 in its first year as expected. The company paid $750,000 for insurance or $3 for every $1,000 in revenue. If the park is wildly successful and revenue increases by 25% in the second year and the rate of $3 for every $1,000 holds true, how much would it pay for insurance? Do you think it’s reasonable for insurance costs to increase proportionally? Why or why not?
Answers
Answer:
1) The amount to be paid as insurance if the revenue increases is $937,000
2) Yes because the total value of the risk insured and the likelihood of the occurrence of the risk both increases
Step-by-step explanation:
1) The given amount in revenue of the Diablo's Domain = $250,000,000
The amount the company paid as insurance = $750,000
The equivalent amount the company paid as insurance = $3 for every $1,000
The percentage amount in revenue the park revenue increases by = 25%
Therefore, the new amount in revenue = 1.25 × $250,000,000 = $312,500,000
The amount to be paid as insurance if the revenue increases = $315,500,000 × 3/1000 = $937,5000
The amount to be paid as insurance if the revenue increases = $937,000
2) It is reasonable for the insurance cost to increase proportionally when the items insured which leads to the increase in revenue increases because the value of the risk insured which is the event of settlement for losses increases as well as the probability of the risk occurring also increases.
rectangular swimming pool is 6 ft deep. One side of the pool is 4.5 times longer than the other. The amount of water needed to fill the swimming pool is 2700 cubic feet. Find the dimensions of the pool.
Answers
Answer: length = 12 feet, width = 54 feet and depth = 6 feet.
Determine the sum of cells A1 and C3. = sume 2) Determine the sum of all rowś from A5 to A27 using the range operator. = sume 3) Determine the largest value in cells D2 and D3. 4) Determine the number of numeric values from rows F5 to F21, cell G12, and cell H9.
Answers
Here are the solutions to the given problems:
1. To find the sum of cells A1 and C3, we simply write the formula as: =SUM(A1,C3)
2. To find the sum of all rows from A5 to A27 using the range operator, we use the formula: =SUM(A5:A27)
3. To determine the largest value in cells D2 and D3, we use the formula: =MAX(D2,D3)
4. To find the number of numeric values from rows F5 to F21, cell G12, and cell H9, we use the formula: =COUNT(F5:F21,G12,H9)
The above formulas are used in Microsoft Excel for performing calculations.
Microsoft Excel is a popular spreadsheet program developed by Microsoft. It is a part of the Microsoft Office suite of productivity software, which also includes programs like Word, PowerPoint, and Outlook.
Excel provides a grid-based interface where users can organize and analyze data. The program uses a collection of cells arranged in rows and columns, forming a worksheet. Each cell can hold various types of data, such as numbers, text, dates, and formulas.
Excel offers a wide range of features and tools to perform calculations, create charts and graphs, manipulate data, and automate tasks. Users can enter data manually or import it from external sources, perform mathematical and statistical calculations, create formulas to link and manipulate data across cells, and use functions for various purposes.
Visit here to learn more about numeric values brainly.com/question/12531105
#SPJ11