Solve the simultaneous equations by substitution
x-3y=-7
x=5-y
Answers
Answer:
x = 2, y = 3
Step-by-step explanation:
x - 3y = - 7 → (1)
x = 5 - y → (2)
Substitute x = 5 - y into (1)
5 - y - 3y = - 7
5 - 4y = - 7 ( subtract 5 from both sides )
- 4y = - 12 ( divide both sides by - 4 )
y = 3
Substitute y = 3 into (2)
x = 5 - 3 = 2
solution is (2, 3 )
Related Questions
Subject:Mathematics

Answers
Answer:
Multiply the length times the width
Step-by-step explanation:
First one finds diameter, third one finds diameter, and fourth one finds triangle. The second one finds the area of a rectangle.
Answer:
I think it is b or length times width
3.31×10 −5
g to micrograms
Answers
3.31×\(10^-^5\) g is equivalent to 0.0331 μg which is obtained by using the conversion factor.
To convert from grams to micrograms, we need to consider the conversion factor that relates the two units. The prefix "micro-" represents a factor of \(10^-^6\), which means there are 1,000,000 micrograms in a gram. Therefore, to convert grams to micrograms, we multiply the given value by 1,000.
In this case, we have 3.31×\(10^-^5\) g. To convert this value to micrograms, we can multiply it by 1,000:
= 3.31×\(10^-^5\) g × 1,000
= 3.31×\(10^-^5\) × 1,000
= 3.31×\(10^-^5\) × \(10^{3}\)
= 3.31×\(10^(^-^5^+^3^)\)
= 3.31×\(10^-^2\)
= 0.0331 μg
Therefore, 3.31×\(10^-^5\) g is equivalent to 0.0331 μg.
Learn more about conversion here:
https://brainly.com/question/27987238
#SPJ11
OT bisects ∠DOG. Find the measure of ∠DOG if ∠DOT = 4x + 4 and ∠TOG = 5x – 3

Answers
Answer:
64
Step-by-step explanation:
OT bisects ∠DOG
⇒ ∠TOG = ∠DOT
5x - 3 = 4x + 4
Add 3 to both sides
5x = 4x + 4 + 3
5x = 4x + 7
Subtract 4x form both sides
5x - 4x = 7
x = 7
∠DOT = 4*7 + 4 = 28 + 4 = 32
∠DOG = 32 + 32 = 64
(b) Estimate each using the normal approximation for the distribution of (outcome - point spread).
Answers
The normal approximation for the distribution of (outcome - point spread is (np(1 - p)0.5
What is Normal Distribution?
An example of a continuous probability distribution is the normal distribution, in which the majority of data points cluster in the middle of the range while the remaining ones taper off symmetrically toward either extreme. The distribution's mean is another name for the center of the range.
Reason:
The number of trials n in the binomial setting and the constant success probability p for each of these trials decide the proper normal distribution to choose. Our binomial variable has a mean of np and a standard deviation of (np(1 - p)0.5, which approximates a normal distribution.
It can be demonstrated using simple mathematics that there are a few circumstances in which we must apply a normal approximation to the binomial distribution. To ensure that both np and n(1 - p) are higher than or equal to 10, the number of observations n must be sufficient, as must the value of p. This is a generalization that is supported by statistical theory. The standard approximation can always be used, however it may not be a very accurate approximation if these requirements are not met.
The normal approximation for the distribution of (outcome - point spread is (np(1 - p)0.5
To learn more about Normal Distribution visit:
brainly.com/question/28030494
#SPJ4
A company that ships crystal bowls claims that bowls arrive undamaged in 95 percent of the shipments. Let the random variable G represent the number of shipments with undamaged bowls in 25 randomly selected shipments. Random variable G follows a binomial distribution with a mean of 23.75 shipments and a standard deviation of approximately 1.09 shipments. Which of the following is the best interpretation of the mean?
a. Every shipment of 25 bowls will have 23.75 undamaged bowls
b. Every shipment of 25 bowls will have 23.75 damaged bowls
c. On average, the company receives 23.75 shipments before receiving the first shipment with a damaged bowl.
d. For all possible shipments of 25, the average number of damaged shipments is equal to 23.75
e. For all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
Answers
The best interpretation of the mean in this situation is: For all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
According to the question, the company claims that bowls arrive undamaged in 95 percent of the shipments. Now, the number of shipments with undamaged bowls in 25 randomly selected shipments is represented by the random variable G.
It follows the binomial distribution with a mean of 23.75 shipments and a standard deviation of approximately 1.09 shipments.
Here, the mean is 23.75.
This means that for all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
Hence, the best interpretation of the mean in this situation is: For all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
Therefore, the correct option is (e) For all possible shipments of size 25, the average number of undamaged shipments is equal to 23.75.
To learn about binomial distribution here:
https://brainly.com/question/15246027
#SPJ11
What is the solution?

Answers
Answer:
the solution means the answer to whatever question / statement
can someone please help :c <3

Answers
Answer:
Step-by-step explanation:

Marta is making 3 servings of fruit salads she adds 1/3 cup blueberries for each serving her measuring cup 1/3 How many times must Marta measure 1/3 cup of blueberries to have enough for the fruit
Answers
Marta needs to measure out 1/3 cup of blueberries three times to have enough for her fruit salad, since she needs a total of 1 cup of blueberries.
To figure out how many times Marta must measure 1/3 cup of blueberries for her fruit salad, we need to first determine how much blueberries she needs in total. Since she is making 3 servings of fruit salad and adding 1/3 cup blueberries for each serving, we can multiply 1/3 by 3 to get the total amount of blueberries needed.
1/3 x 3 = 1 cup
So Marta needs a total of 1 cup of blueberries for her fruit salad. Now we can determine how many times she needs to measure out 1/3 cup of blueberries. We can divide the total amount needed (1 cup) by the amount in each measurement (1/3 cup):
1 cup ÷ 1/3 cup = 3
So Marta needs to measure out 1/3 cup of blueberries 3 times in order to have enough for her fruit salad.
In summary, Marta needs to measure out 1/3 cup of blueberries three times to have enough for her fruit salad, since she needs a total of 1 cup of blueberries.
To know more about measuring visit: https://brainly.com/question/27097057
#SPJ11
A cookie recipe for 60 cookies calls for 4 cups of flour. How much flour is needed to make 90 cookies?
Answers
Answer: 6 cups
Step-by-step explanation:
60 cookies = 4 cups
60 + 30 = 90, and half of 60 is 30. So half of 4 cups is 2 cups.
4 cups plus 2 cups is 6 cups!
Answer:
6 cups
Step-by-step explanation:
because if you / the 60 by 4 you would see that 1 cup = 15 cookies. Then add 15 till you get to 90
Point Z is equidistant from the sides of ARST. C R Z A B S Which must be true? A. SZ&TZ
B. RZ =R BZ
C. CTZ = ASZ
D. ASZ=ZSB
Answers
Answer:
B. RZ =R BZ
Step-by-step explanation:
Since point Z is equidistant from the sides of ARST, it lies on the perpendicular bisectors of both sides. Therefore, CZ and SZ are perpendicular bisectors of AB and ST, respectively.
Option B is true because point R lies on the perpendicular bisector of AB, and therefore RZ = RB.
Answer: vv
Step-by-step explanation:
Since point Z is equidistant from the sides of ARST, it lies on the perpendicular bisector of the sides ST and AR.
Therefore, we can draw perpendiculars from point Z to the sides ST and AR, which intersect them at points T' and R', respectively.
Now, let's examine the options:
A. SZ & TZ: This is not necessarily true, as we do not know the exact location of point Z. It could lie anywhere on the perpendicular bisector of ST, and the distance from Z to S and T could be different.
B. RZ = RB: This is true, as point Z lies on the perpendicular bisector of AR, and is therefore equidistant from R and B.
C. CTZ = ASZ: This is not necessarily true, as we do not know the exact location of point Z. It could lie anywhere on the perpendicular bisector of AR, and the distances from Z to C and A could be different.
D. ASZ = ZSB: This is not necessarily true, as we do not know the exact location of point Z. It could lie anywhere on the perpendicular bisector of ST, and the distances from Z to A and B could be different.
Therefore, the only statement that must be true is option B: RZ = RB.
Melissa walks 3 miles to the house of a friend and returns home on a bike. She averages 4 miles per hour faster when cycling than when walking, and the total time for both trips is two hours. Find her walking speed (HINT: Write an expression that represents the time it takes for Melissa to walk to her friends house, and then write an expression for the time it takes to cycle back. The sum of these expressions is equal to the total time of the trip.)
Answers
Answer:
walking speed is 2 m/s
Step-by-step explanation:
given data
distance between Melissa and friend = 3 mile
total time of the trip = 2 hour
solution
we consider here
walking speed = s₁
bike speed = s₂
so s₂ = s₁ + 4 .................1
and
time is express as
time = distance ÷ speed .................2
so time for Melissa to friend reach = 3 ÷ s₁
and time for return from her friend = 3 ÷ s₂
so put this value in equation 2 we get
time = 3 ÷ s₁ + 3 ÷ s₂
2 = \(\frac{3}{s_1} + \frac{3}{s_1 + 4}\)
solve it and we will get
s₁² + s₁ - 6 = 0
s₁ = 2 m/s
so walking speed is 2 m/s
What is the answer for - 2x + 3 > 15
Answers
Answer:
X < -6
Step-by-step explanation:
What is the equation of the line that passes through the point (0,-5) and is parallel to the graph y=9x?
Answers
Answer:
llll
Step-by-step explanation:
gfhg
simplify and find the absolute value

Answers
Step-by-step explanation:
Explanation is in the attachmenthope it is helpful to you

Step-by-step explanation:
{(-10)-(-15)÷5}
-10+15÷5
-10+3
= -7
Object B has a mass of 10kg. Object b collides with another object. If the momentum of object b after collision is 18kg•m/s18kg.m/s, its volocity is_____m/s
Answers
Answer:
Step-by-step explanation:
Solve the following equation for . 1 a2 d2 d2 + 2 ℏ2 |E| = 0, Assume a standard trial solution = A exp(iB). (Use the following as necessary: a, E, , and ℏ.) A = B = Find the allowed energies and angular momenta. (Use the following as necessary: a, , ℏ, and n, the quantum number.) E =
Answers
The allowed energies are: E = ± n2 ℏ2/(2ma2) And the allowed angular momenta are: L = n ℏ
To solve the equation 1 a2 d2 d2 + 2 ℏ2 |E| = 0, we assume a standard trial solution = A exp(iB).
First, we take the second derivative of the trial solution:
d2/dx2 (A exp(iB)) = -A exp(iB)B2
Next, we substitute the trial solution and its derivatives into the original equation:
1/a2 (-A exp(iB)B2) + 2 ℏ2 |E| A exp(iB) = 0
Simplifying and dividing by A exp(iB), we get:
-B2/a2 + 2 ℏ2 |E| = 0
Solving for E, we get:
|E| = B2/(2 ℏ2 a2)
To find the allowed energies and angular momenta, we need to use the following equation:
E = ℏ2 n2/(2ma2)
where n is the quantum number and m is the mass of the particle.
Setting these two equations equal to each other and solving for B, we get:
B = n ℏ
Substituting this into the equation for |E|, we get:
|E| = n2 ℏ2/(2ma2)
Know more about derivative here:
https://brainly.com/question/30365299
#SPJ11
Solve the following quadratic equation by factoring:
x^2 + 2x - 8 = 0
Answers
Answer: x = -4 and x = 2.
To factor a quadratic equation in the form of x^2 + bx + c = 0, we need to find two numbers that when multiplied together, give us c, and when added or subtracted, give us b.
We need to find two numbers whose product is -8 and whose sum is 2. These numbers are 4 and -2, so we can write:
x^2 + 2x - 8 = (x + 4)(x - 2) = 0
Setting each factor to zero, we get:
x + 4 = 0 or x - 2 = 0
Solving for x in each equation, we get:
x = -4 or x = 2
So, the solutions to the equation x^2 + 2x - 8 = 0 are x = -4 and x = 2.
What are the Examples of Adding Fractions with Unlike Denominators
Answers
2/3 + 1/4 = 11/12
Fractions are very important in many areas such as math, physics, engineering, chemistry and many more, understanding how to add fractions with unlike denominators is a fundamental skill that will help you in many aspects of your life.
Adding fractions with unlike denominators can be a bit tricky, but with the right understanding and techniques, it's definitely doable.
When we add fractions with unlike denominators, we need to first find a common denominator. A common denominator is a number that is a multiple of both denominators. Once we have a common denominator, we can add the fractions as usual by adding the numerators and keeping the denominator the same.
Here are a few examples of adding fractions with unlike denominators:
2/3 + 1/4
We can find a common denominator by finding the least common multiple (LCM) of 3 and 4. The LCM of 3 and 4 is 12.
So, we can convert 2/3 to 8/12 by multiplying the numerator and denominator by 4.
We can convert 1/4 to 3/12 by multiplying the numerator and denominator by 3.
Now we can add the fractions by adding the numerators: 8/12 + 3/12 =
1/5 + 2/7
We can find a common denominator by finding the least common multiple (LCM) of 5 and 7. The LCM of 5 and 7 is 35.
So, we can convert 1/5 to 7/35 by multiplying the numerator and denominator by 7.
We can convert 2/7 to 10/35 by multiplying the numerator and denominator by 5.
So, we can convert 3/4 to 9/12 by multiplying the numerator and denominator by 3.
We can convert 1/3 to 4/12 by multiplying the numerator and denominator by 4.
Now we can add the fractions by adding the numerators: 9/12 + 4/12 = 13/12
So, 3/4 + 1/3 = 13/12
It's important to note that when adding fractions, it's also important to simplify the final result if possible.
To know more about FRACTIONS refer here
brainly.com/question/10354322#
#SPJ11
A map uses a scale of 12\frac{1}{2}
2
1
centimeter = 75 kilometers. The actual distances between various cities are given below. Find the distance between the cities on the map. (centimeters)
#4
50 kilometers
Answers
The distance between the two cities on the map is 8.33 cm.
To find out the distance between two cities on a map with a given scale, we use the formula: distance on map = actual distance ÷ scale; Given, the actual distance between the two cities = 50 km; Given, the scale of the map = 12 1/2 cm = 75 km.
Let the distance between two cities on the map be x cm. Then, we can say that,50 ÷ 75 = x ÷ 12.5. Simplifying the above equation, we get, x = (50 × 12.5) ÷ 75= 8.33 cm. Therefore, the distance between the two cities on the map is 8.33 cm.
Learn more about distance here:
https://brainly.com/question/11599816
#SPJ11
Find the measure of angles 1,2 and 3
Answers
Answer:
??
Step-by-step explanation:
where is the question
Find X.
Hint: T is an inscribed angle that creates arc WS. Arc WS can be found by adding arcs WR and RS together.
See picture for full problem. Please and thank you so much!

Answers
Answer:
x=13
Step-by-step explanation:
The attached photo might help

Taylor bought a watch onsale for 60% off the originalprice, and another 10% off thediscounted price. If the watchoriginally cost $82, what wasthe final sale price?
Answers
Original Cost - $82
First part: Apply the 60% off discount
Convert first the 60% into decimal form
60% ÷ 100% = 0.6
Multiply it to the original cost to determine the discount
$82 ˣ 0.6 = $49.2
Subtract the discount to the original price, to determine the discounted price.
$82 - $49.2 = $32.8
Second part:
The discounted price is now $32.8 for which we will apply another 10% discount.
Again, convert 10% into decimal
10% ÷ 100% = 0.1
Multiply it to the discounted price, to determine the second discount.
$32.8 ˣ 0.1 = $3.28
Subtract the discount to the already discounted price.
$32.8 - $3.28 = $29.52
Therefore, the final sale price of the watch is at $29.52.
convert 80 km per hour and 120 km per hour to meters per second
Answers
hi brainly user! ૮₍ ˃ ⤙ ˂ ₎ა
⊱┈────────────────────────┈⊰
\(\large \bold {ANSWER}\)
\(\large \boxed { \large \sf \green{ 80 km/h = 22.22 m/s }}\)\(\large \boxed { \large \sf \green{ 120 km/h = 33.33 m/s }}\)\(\large \bold {SOLUTION}\)
The first thing we must do is convert kilometers to meters. We will do this by multiplying by 1,000, since 1 km corresponds to 1,000 meters.
80*1000 = 80,000120*1000 = 120,000Now that we've done that, let's divide the values by 3,600, because an hour is 60 minutes, and each minute is 60 seconds, so 60*60 is 3,600.
\(\frac{80.0\not0\not0}{3.6\not0\not0}=22.22\)
\(\frac{120.0\not0\not0}{3.6\not0\not0}=33.33\)
Hence, 80 km/h = 22.22 m/s, 120 km/h = 33.33 m/s
To convert a value from km/h to m/s and vice versa, we can always use the lengthy formula, but here’s a short version of it which will always come in handy.
• To Convert km/h to m/s
= km/h * 5/18
• To Convert m/s to km/h
= m/s * 18/5
80 km/h to m/s
= 80 * 5/18
= 400/18
=> 22.22 m/s
120 km/h to m/s
= 120 * 5/18
= 600/18
=> 33.33 m/s
answer two questions about equations A and B:
A. x/4+1=-3
B. x+4=-12
1) how can we get equation B from equation A?
choose 1 answer:
(Choice A) rewrite one side (or both) using the distributive property
(Choice B) rewrite one side (or both) by combining like terms
(Choice C) multiply/divide only one side by a non zero constant
(Choice D) multiply/divide both sides by the same non zero constant
2) based on the previous answer ,are the equations equivalent? in other words ,do they have the same solution?
choose 1 answer:
(Choice A) yes
(Choice B) no
Answers
Answer:it’s d and yes
Step-by-step explanation:
(2,-1) is one of many solutions to the inequality x-3y<1
Answers
We will have the following:
\(3y<1\Rightarrow y<\frac{1}{3}\)So, the point (2, -1) is one of the many solutions.
PROBLEM SOLVING
Question 8
Three sets of traffic lights (A, B and C) all turn red at 9 a.m. exactly. Light set A turns red every 2 minutes, light
set B turns red every 3 minutes and light set C turns red every 5 minutes. How long does it take for all three
lights to turn red again at the same time?
Answers
2*3*5=30 minutes
just tell me the slope of the line and where to plot the segments on the graph
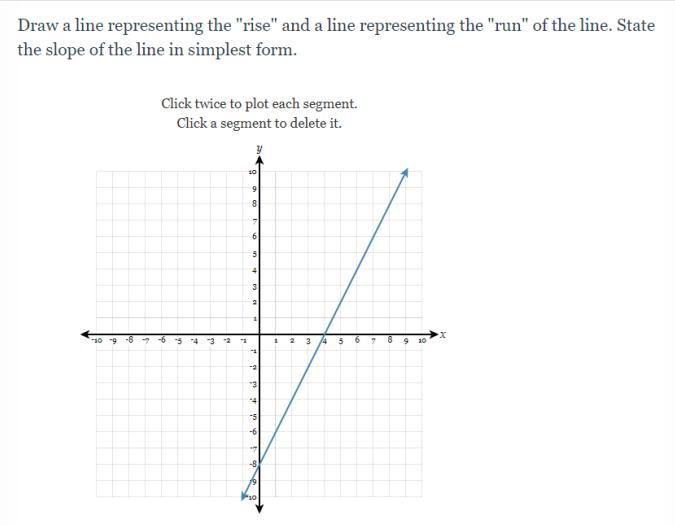
Answers
Answer:
The slope is 2
Step-by-step explanation:
Take any two points on the line. I am going to use the points (0,-8) and (4,0) Points are in the form (x,y) The y values form the two points is 0 and -8. The x values are 4 and 0.
The slope is the change in y over the change in x.
\(\frac{0- -8}{4-0}\) = \(\frac{8}{4}\) = 2
Use a table to show the sample space of two-digit numbers using the digits 9,4,5,8
Answers
the sample space of two-digit numbers using the digits 9, 4, 5, and 8 consists of 16 possible outcomes, and we can list all these outcomes in a table as shown above.
How to solve the question?
To create a sample space of two-digit numbers using the digits 9, 4, 5, and 8, we need to consider all possible combinations of these digits. We can list all possible outcomes in a table where each digit represents a column and each combination represents a row.
The first digit can be any of the four digits, and the second digit can also be any of the four digits, including the same digit as the first. Therefore, the total number of outcomes is 4 x 4 = 16.
Here is the sample space of two-digit numbers using the digits 9, 4, 5, and 8:
9 4 5 8
9 99 94 95 98
4 49 44 45 48
5 59 54 55 58
8 89 84 85 88
As shown in the table, the first digit can be any of the four digits, and the second digit can also be any of the four digits. For example, the first row shows that the possible two-digit numbers starting with 9 are 99, 94, 95, and 98. Similarly, the second row shows that the possible two-digit numbers starting with 4 are 49, 44, 45, and 48, and so on.
In conclusion, the sample space of two-digit numbers using the digits 9, 4, 5, and 8 consists of 16 possible outcomes, and we can list all these outcomes in a table as shown above.
To know more about digits visit :-
https://brainly.com/question/26856218
#SPJ1
Find all the zeros of f(x)=(x-3)^2-49
Answers
The zeros of the given polynomial function are x=-4 and x=10.
The given polynomial function is f(x)=(x-3)²-49.
Now, f(x)=(x-3)²-7²
The zeros of polynomial refer to the values of the variables present in the polynomial equation for which the polynomial equals 0.
Here, (x-3)²-7²=0
(x-3+7)(x-3-7)=0 (∵a²-b²=(a+b)(a-b))
(x+4)(x-10)=0
x=-4 and x=10
Therefore, the zeros of the given polynomial function are x=-4 and x=10.
To learn more about the polynomial function visit:
https://brainly.com/question/12976257.
#SPJ1
A track coach records the number of miles that he ran per day over the month. The stem-and-leaf plot below summarizes this data.
Answers
Answer:
\(Mean = 6.70\)
Step-by-step explanation:
Given
See attachment for plot
Required
The mean of the plot
Mean is calculated as:
\(Mean = \frac{\sum x}{n}\)
Where
\(n = 20\)
Using the given key to read, the plot;
We have:
\(Mean = \frac{3.00+3.25+4.25+5.00+..........+8.75+9.50}{20}\)
\(Mean = \frac{134.00}{20}\)
\(Mean = 6.70\)
