(solve the literal equation for y.)
6 - 3y = -6
Answers
Answer:
4
Step-by-step explanation:
Related Questions
Factors for three-sigma control limits for \( \bar{x} \) and \( R \) charts: 1) What's the upper control limit (UCL) with three-sigma limits for the mean of software upgrade time in minutes? (Round yo
Answers
The upper control limit (UCL) with three-sigma limits for the mean of software upgrade time in minutes can be determined by multiplying the standard deviation by three and adding it to the mean. However, since the mean and standard deviation are not provided in the question, a specific numerical answer cannot be given.
In statistical process control, the three-sigma control limits are commonly used to establish the range within which a process is considered to be in control. The three-sigma limits represent a statistical measure that encompasses approximately 99.7% of the data if the process is stable and normally distributed.
By calculating the UCL using the mean and standard deviation, organizations can set an upper boundary that helps monitor the software upgrade time. If any data point exceeds the UCL, it suggests a potential variation or issue in the process, warranting further investigation and corrective actions to ensure the software upgrade time remains within acceptable limits. The UCL serves as a reference point for identifying significant deviations from the expected mean and facilitates continuous process improvement in software upgrade operations.
Learn more about standard deviation here;
brainly.com/question/29115611
#SPJ11
In a county the conviction rate for speeding is 85%. Estimate the probability that of the next 100 speeding summonses issued, there will be at least 90 convictions.
Answers
The estimated probability that of the next 100 speeding summonses issued, there will be at least 90 convictions is about 0.9997 or 99.97%.
The conviction rate for speeding in the county is 85%, it means that out of every 100 speeding summonses issued, 85 are likely to result in convictions. Therefore, we can assume that the probability of a conviction in any given case is 0.85 or 85%.
To estimate the probability that of the next 100 speeding summonses issued, there will be at least 90 convictions, we can use the binomial distribution formula. Let X be the number of convictions out of the 100 summonses. Then,
P(X ≥ 90) = 1 - P(X < 90)
= 1 - Σ P(X = i) for i = 0 to 89
where Σ denotes the sum from i = 0 to 89.
Using the binomial distribution formula, we can calculate the probability of getting exactly i convictions out of 100 summonses as:
P(X = i) = (100 choose i) * 0.85^i * 0.15^(100-i)
where (100 choose i) denotes the binomial coefficient, which represents the number of ways to choose i items out of 100.
Plugging this formula into the above equation and using a calculator or statistical software, we get:
P(X ≥ 90) = 1 - Σ P(X = i) for i = 0 to 89
= 1 - 0.0003 (approx.)
= 0.9997 (approx.)
Therefore, the estimated probability that of the next 100 speeding summonses issued, there will be at least 90 convictions is about 0.9997 or 99.97%. This suggests that it is highly likely that at least 90 out of 100 speeding summonses will result in convictions, given the high conviction rate of 85% in the county.
To estimate the probability that of the next 100 speeding summonses issued, there will be at least 90 convictions, we'll use the binomial probability formula:
P(X ≥ 90) = Σ [C(n, k) * p^k * (1-p)^(n-k)]
Here, n = 100 (number of summonses), p = 0.85 (conviction rate for speeding), and k represents the number of successful convictions (90 to 100).
Step 1: Calculate the individual probabilities for k = 90 to 100:
For each value of k from 90 to 100, compute the binomial probability using the formula. C(n, k) represents the number of combinations of choosing k convictions from n summonses.
Step 2: Sum the individual probabilities:
Add up the probabilities calculated in Step 1 to find the total probability of having at least 90 convictions out of 100 speeding summonses.
By following these steps, you can estimate the probability that of the next 100 speeding summonses issued, there will be at least 90 convictions.
Learn more about binomial at: brainly.com/question/13870395
#SPJ11
What value of x will make the question true?
(Starroot 5 endRoot) (Startroot 5 endRoot) =!x
Answers
The question does not make sense because the two statements in the question are equal to each other. Therefore, no value of x will make the question true.
What is equal?Equality is the state of being equal, especially in status, rights, and opportunities. Equality is a fundamental human right, and is essential for the achievement of peace and development. Equality means that everyone has the right to be treated the same and have access to the same opportunities, regardless of their gender, race, ethnicity, religion, sexual orientation, or economic background. Equality is important for a just and fair society, and is a cornerstone of democracy. It is essential for the advancement of human rights and social justice.
To learn more about equal
https://brainly.com/question/17145398
#SPJ1
Andre runs at a constant speed, 5 meters every 2 seconds. how long does it take him to run 91 meters at this rate
Answers
Answer: 36.4 seconds
(Unitary method)
5 meters take 2 seconds
1 meter takes 2/5 seconds
91 meter takes 2/5 * 91 --> 36.4 seconds
The time taken by Andre to run 91 meters is 36.5 seconds.
What is the speed of an object?Speed is the rate at which an object's position changes, measured in meters per second. For example, if an object starts at the origin, and then moves three meters in three seconds, its speed is one meter per second. The equation for speed is simple: distance divided by time
Given here: Distance travelled by Andre=5 meters in time t=2seconds
Thus Andre's speed = 5/2
=2.5 m/sec
Thus time taken to run 91 m is = 91/2.5
=36.5 seconds
Hence, The time taken by Andre to run 91 meters is 36.5 seconds.
Learn more about speed here:
https://brainly.com/question/28224010
#SPJ2
linear approximation help pretty pls

Answers
Answer:
A
Step-by-step explanation:
Our function is
\( \frac{1}{2} \pi( {x}^{2} )\)
We need to estimate v(2.98) using V(3).
Variables:
What we are trying to find is V(2.98). We will later plug in 2.98 into the tangent line approximation.
We are going to use V'(3) for the slope of the tangent line. We will use V(3) later for the tangent line approximation.
So first, let solve for
V'(x).
\( \frac{1}{2} \pi( {x}^{2} )\)
1/2 pi is a constant so
\( \frac{1}{2} \pi( \frac{d}{dx} (x {}^{2} )\)
\( \frac{1}{2} \pi(2x)\)
\(v'(x) =( \pi)x\)
Let x=3,
\(v'(3) = 3\pi\)
Let find v(3).
\( \frac{1}{2} \pi( {3}^{2} ) = 4.5\pi\)
The tangent line equation is
\(f(x) = f(a) + f'(a)(x - a)\)
x is 2.8
a. is 3.
\(f(2.8) = f(3) + f'(3)(2.8 - 3)\)
\(f(2.8) = 4.5\pi + 3\pi( - 0.2)\)
Disclaimer: F(x) is V(x).
\(f(2.8) = 4.5\pi - 0.6\pi\)
\(f(2.8) = 3.9\pi = 12.25\)
The closest here is A
Lindsey is working really hard to improve her grade. on her first quiz she scored 67 point, on her second she scored 71, and on her third she scored 75. her scores continue to increase at the same rate. write a recursive and explicit formula for this geometric sequence.
Answers
The recursive formula for Lindsey's scores is aₙ = aₙ₋₁ \(\times\) r, and the explicit formula is aₙ \(= 67 \times r^{(n-1).\)
To find the recursive and explicit formulas for the given geometric sequence, let's analyze the pattern of Lindsey's scores.
From the given information, we can observe that Lindsey's scores are increasing at the same rate.
This suggests that the scores form a geometric sequence, where each term is obtained by multiplying the previous term by a common ratio.
Let's denote the first term as a₁ = 67 and the common ratio as r.
Recursive Formula:
In a geometric sequence, the recursive formula is used to find each term based on the previous term. In this case, we can write the recursive formula as:
aₙ = aₙ₋₁ \(\times\) r
For Lindsey's scores, the recursive formula would be:
aₙ = aₙ₋₁ \(\times\) r
Explicit Formula:
The explicit formula is used to directly calculate any term of a geometric sequence without the need to calculate the previous terms.
The explicit formula for a geometric sequence is:
aₙ = a₁ \(\times r^{(n-1)\)
For Lindsey's scores, the explicit formula would be:
aₙ \(= 67 \times r^{(n-1)\)
In both formulas, 'aₙ' represents the nth term of the sequence, 'aₙ₋₁' represents the previous term, 'a₁' represents the first term, 'r' represents the common ratio, and 'n' represents the term number.
For similar question on recursive formula.
https://brainly.com/question/31157431
#SPJ8
The product of (5+3√2) (5-3√2) is
Answers
Answer:
7
Step-by-step explanation:
First use the (a-b) and (a+b) = a^2 - b^2 which is equal to 25 - 9 x 2
then you multiply 9 x 2 which is 18 so 25 - 18 thus 7. The trick is to remember the rules.
A space research pod goes around the earths circumference in 2 hours. Find it’s angular velocity in radians per second and it’s linear speed in feet per minute and in miles per hour.
Answers
Let's find the angular velocity:
\(\begin{gathered} \omega=2\pi f \\ f=\frac{1}{T} \\ \omega=\frac{2\pi}{T} \\ \omega=\frac{2\pi}{2}=\frac{\pi rad}{h} \end{gathered}\)We need to find the velocity in radians per second, so:
\(\pi\frac{rad}{h}\times\frac{1h}{3600s}=\frac{\pi}{3600}\approx\frac{0.0008727rad}{s}\)Let's find the linear speed:
\(v=\omega\cdot r\)\(v=\omega\cdot(6371\operatorname{km})=\frac{5559.74632m}{s}\)We need to express this speed in feet per minute, so:
\(5559.746332\frac{m}{s}\times\frac{3,28084ft}{1m}\times\frac{60s}{1\min}=\frac{1094438.289ft}{\min }\)Now in miles per hour:
\(1094438.289\frac{ft}{\min}\times\frac{1mi}{5280ft}\times\frac{60\min }{1h}=\frac{12436.79874mi}{h}\)Mrs. Rashad Is baking 3 ples, She needs 1 /6 cups of strawberries for each ple. How many cups of strawberries does she need in all?
Answers
Answer: 3/6 or 1/2
Step-by-step explanation: 1/6 x 3 = 3/6 or simplified form 1/2.
Answer:
1/2 cups of strawberries is required.
Step-by-step explanation:
1 pie = 1/6 cups of strawberries
=> 3 pies = 1/6 x 3
=> 3 pies = 1/2 cups of strawberries.
Hoped this helped.
Which expressions are equivalent to √/32?
4√8
08
2√8
4√2
16
16√2
Answers
Answer: 4√2
square root of a number is the factor that we can multiply by itself to get that number.
The square root symbol is also called as a RADICAL.
Perfect squares are the squares of the integers also called as square numbers.
to find the square root of non-perfect squared numbers we have to check the number with a near-perfect squared numbers
how to find square root of non perfect squared numbers:
If we can't figure out what factor multiplied by itself will result in the given number, we can make a factor tree.
Factor tree of 32 = 2*2*2*2*2
= (2*2) * (2*2) *2
= (4)2 *2
Therefore √/32 = √/2*2*2*2*2
= √/(4)2*2
= 4√/2
learn more about square roots here:
https://brainly.com/question/428672
https://brainly.com/question/3617398
#SPJ9
pounds. She uses 17,6056 fl oz of water for her recipe. If this is equivalent to 500 ml, determine the conversion rate between fl oz and ml.
Answers
the conversion rate between fluid ounces and milliliters is 0.0352 ml/fl oz.
What is a proportion?
A proportion is a mathematical relationship between two ratios that states that they are equal. It can be expressed as an equation of the form:
a/b = c/d
Where a, b, c, and d are numbers and b and d are not equal to 0.
To determine the conversion rate between fluid ounces (fl oz) and milliliters (ml), we can use the fact that 17.6056 fl oz is equivalent to 500 ml.
We can set up a proportion:
17.6056 fl oz / 500 ml = x / 1 ml
Where x is the conversion rate.
We can solve for x by cross-multiplying:
17.6056 * 1 ml = 500 * x
17.6056 ml = 500 * x
Dividing both sides by 500:
x = 17.6056 ml / 500 = 0.0352 ml/fl oz
Hence, the conversion rate between fluid ounces and milliliters is 0.0352 ml/fl oz.
To learn more about the proportion, visit:
https://brainly.com/question/1496357
#SPJ1
Anelle is in charge of bringing in dry erase markers for everyone in her math group to use to work on a project. She brings 3 markers for each person in her group and 5 extra markers for everyone to share. If Janelle brings in 23 markers in all, which equation represents the information?
Answers
Answer:
3x + 5 = 23
Step-by-step explanation:
Let x represents the number of persons in her group.
Since she brings 3 markers for each person, then number of markers brought for persons in her group = 3x.
She brings 5 extra markers for each person to share.
Thus, total markers she brought is now;
3x + 5
She brought 23 markers in all.
Thus, equation that represents the information is;
3x + 5 = 23
Please help, I’ll mark your answer as brainliest.

Answers
Answer:
it'sssssss 2.51
Step-by-step explanation:
========≈==================
Which of these strategies would eliminate a variable in the system of equations?
2x- 6y=6
6x - 4y = 2
Choose all answers that apply: more than 1
Multiply the bottom equation by 3 then subtract the bottom equation from the top equation
Multiply the bottom equation by -3/2 then add the equations.
Multiply the top equation by-3. then add the equations
Answers
Answer:
Multiply the bottom equation by -3/2 then add the equations.
Multiply the top equation by-3. then add the equations
Step-by-step explanation:
Given the simultaneous equation
2x- 6y=6 ... 1
6x - 4y = 2 ... 2
To eliminate a variable, we have to make the coefficient of one of the variable to be the same.
Multiply equastion 1 by -3
-6x+18y= -18
6x - 4y = 2
Add the result:
-6x + 6x + 18y-4y = -18+2
18y-4y = -18+2
14y = -18
y = -9/7
Another way is to Multiply the bottom equation by -3/2 then add the equations.
Multiplying equation 2 by -3/2 will give;
6x(-3/2) - 4y(-3/2) = 2(-3/2)
-9x + 6y = -3
Add to equation 1;
2x- 6y=6
-9x + 2x + 0 = -3+6
-7x = 3
x = -3/7
Hence the correct two options are;
Multiply the bottom equation by -3/2 then add the equations.
Multiply the top equation by-3. then add the equations
Ben is x cm tall.
Kieran is 8 cm taller than Ben.
Bianca is 2 cm shorter than Ben.
Write an expression, in terms of x, for the mean of their heights in centímetres.
Give your answer in its simplest form.
Answers
hope this helps you understand !!

Answer:
x + 2
Step-by-step explanation:
Ben : x cm
Kieran: (x + 8) cm
Bianca: (x - 2) cm
Mean of their heights = \(\frac{Sum of their heights}{Number of people} = \frac{x + (x + 8) + (x - 2)}{3}\)
= \(\frac{x + x + 8 + x - 2}{3}\) (Expand the brackets)
= \(\frac{x + x + x + 8 - 2}{3}\) (Bring all the like terms together)
= \(\frac{3x + 6}{3}\) (Simplify the two sets of like terms)
= \(\frac{3(x + 2)}{3}\) (Extract the common factor '3' in the numerator)
= (x + 2) cm (\(\frac{3}{3} = 1\))
what is 2÷3 2/3 in simplest form
Answers
Answer:
here it is
Step-by-step explanation:
you can see, 2/3 cannot be simplified any further, so the result is the same as we started with. Not very exciting, I know, but hopefully you have at least learned why it cannot be simplified any further!
A boat traveled downstream a distance of 18 mi and then came right back. If the speed of the current was 6 mph and the total trip took 2 hours and 15 minutes, find the average speed of the boat relative to the water. The boat had an average speed of ___ mph relative to the water. (Simplify your answer.)
Answers
Average speed of the boat relative to the water = (Downstream speed + Upstream speed)/2= [(x + 6) + (x - 6)]/2= 2x/2= x= 24 mph Therefore, the average speed of the boat relative to the water is 24 mph.
A boat traveled downstream a distance of 18 miles and then came right back. If the speed of the current was 6 mph and the total trip took 2 hours and 15 minutes, find the average speed of the boat relative to the water.The speed of the boat in still water is x mph.Speed of the current
= 6 mph Downstream speed
= (x + 6) mph Upstream speed
= (x - 6) mph Distance traveled downstream
= 18 miles Distance traveled upstream
= 18 miles Total time taken
= 2 hours 15 minutes
= 2 × 60 + 15
= 135 minutes Total time taken downstream + Total time taken upstream
= Total time taken for the round trip Using the formula, Total distance
= Speed × Time 18
= (x + 6) × (135/60)/2 + (x - 6) × (135/60)/2
= (x + 6) × (135/60)/2 + (x - 6) × (135/60)/2x
= 24 mph .Average speed of the boat relative to the water
= (Downstream speed + Upstream speed)/2
= [(x + 6) + (x - 6)]/2
= 2x/2
= x
= 24 mph Therefore, the average speed of the boat relative to the water is 24 mph.
To know more about Average visit:
https://brainly.com/question/24057012
#SPJ11
h(t)=( 1)/(3) t-10, find h(t) when t =27 and when t= -15
Answers
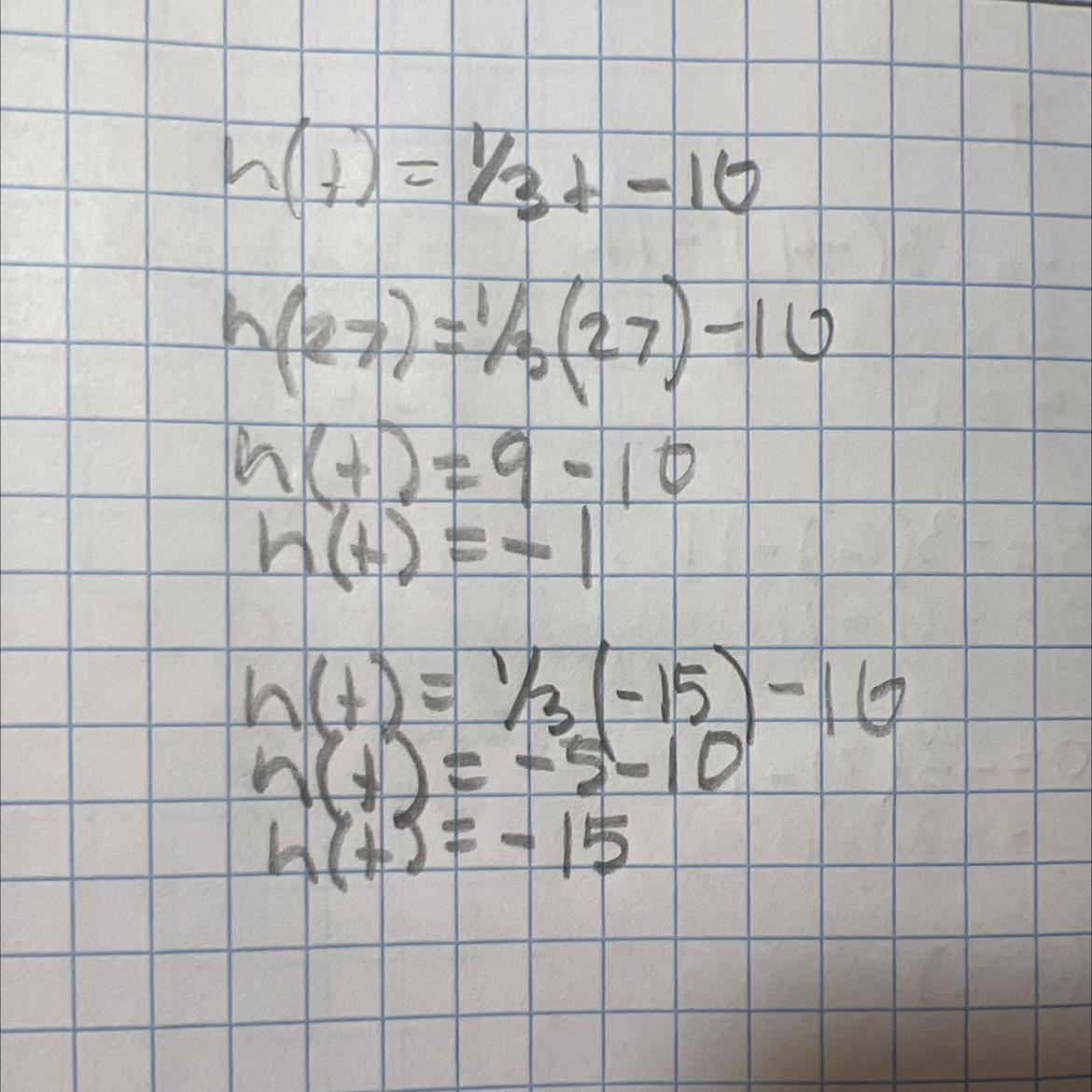
1: 1. Jonathan is building a chicken farm in 2023. The initial population of his farm is 2850 chickens. The population of his chicken farm grows at a rate of 3% annually.
(a) Write an exponential equation that can be used model the population of the farm t years after 2023.
(b) Using this equation, estimate the population of the chicken farm in 2045. Please round to the nearest chicken (no partial chickens, please!)
2: Please answer parts a-c:
Sketch the graph of the function f(x)=2^x.
If f(x) is translated 4 units down, what is the equation of the new function g(x)?
Graph the transformed function g(x) on the same grid.
**Both functions must be present on your graph.
3: 3. Alyssa started a savings account with an initial deposit of $1600. The account earns 4.12% interest compounded quarterly.
(a) Write an exponential equation to represent the amount of money in the account after t years.
(b) Using this equation, calculate how much money will be in the account after 7 years, assuming Alyssa makes no additional deposits or withdrawals. (Please round to the nearest cent)
Answers
after 7 years, the amount of money in the account will be $2197.68. According to the question.
How to solve the question?
1:
(a) The exponential equation that can be used to model the population of the chicken farm t years after 2023 is:
P(t) = 2850 x 1.03 in power t
where P(t) is the population of the chicken farm after t years.
(b) To estimate the population of the chicken farm in 2045, we need to find P(22), as 2045 - 2023 = 22.
P(22) = 2850 x 1.03²²
= 4405.56 (rounded to the nearest chicken)
Therefore, the estimated population of the chicken farm in 2045 is 4406.
2:
(a) The graph of the function f(x) = 2ˣ is an increasing exponential curve that passes through the point (0,1) and has a vertical asymptote at x = -∞.
(b) To find the equation of the new function g(x), which is the transformation of f(x) 4 units down, we need to subtract 4 from the function:
g(x) = f(x) - 4
= 2ˣ - 4
(c) The graph of the transformed function g(x) = 2ˣ - 4 is the same as the graph of f(x) = 2ˣ but shifted 4 units downward.
3:
(a) The exponential equation that represents the amount of money in Alyssa's savings account after t years, assuming no additional deposits or withdrawals, is:
A(t) = 1600 x (1 + 0.0412/4) in power (4t)
where A(t) is the amount of money in the account after t years.
(b) To calculate how much money will be in the account after 7 years, we need to find A(7):
A(7) = 1600 x (1 + 0.0412/4)²⁸
= 2197.68 (rounded to the nearest cent)
Therefore, after 7 years, the amount of money in the account will be $2197.68.
To know more about cost estimate visit :-
https://brainly.com/question/27993465
#SPJ1
A cylindrical tin, 7cm high, is closed at one end. If it's total surface area is 462cm², calculate it's radius
Answers
Height = 7cm
Surface area = 462 cm2
The surface area of a cylinder is equal to the area of each circle ( pi x radius^2) plus the area of the side (2 pi x radius x height)
Surface area of a cylinder = pi r2 + pi r2 + 2pi r h
Since it is closed at one end, we only add one circle area:
S = pi r2 + 2pi r h
Replacing with the values given:
462 = pi r^2 + 2pi (r) 7
462 = pi r^2+ 43.98 r
462 -44r = pi r^2
(462-44r)/pi = r^2
147-14r = r^2
0= r^2 +14r -147
(r+21 ) (r-7)=0
r=-21 or r=7
Since it can be negative:
radius = 7
could you help me out
Answers
we must use trigonometric ratios to solve the right triangle
i will use the cosine
\(\begin{gathered} \cos (\alpha)=\frac{A}{H} \\ \end{gathered}\)where alpha is the angle, a the adjacent side and H the hipotenuse,
so replacing
\(\cos (73)=\frac{6}{x}\)now solve for x
\(\begin{gathered} x=\frac{6}{\cos (73)} \\ \\ x=20.52 \end{gathered}\)so the right option is I

The soft goods department of a large department store sells 175 units per month of a certain large bath towel. The unit cost of a towel to the store is \( \mathbf{S 2 . 5 0} \) and the cost of placing
Answers
The optimal order quantity is 1256 units and the minimum total cost is S3150.04. The soft goods department of a large department store sells 175 units per month of a certain large bath towel. The unit cost of a towel to the store is S2.50 and the cost of placing an order is S375.
In this problem, the order quantity (Q) will be calculated using the economic order quantity (EOQ) formula as follows:
EOQ = √[(2DS)/H] Where: D = Annual Demand, S = Cost of placing an order, H = Carrying cost per unit per year, Carrying cost per unit per year can be computed using the following formula: H = iC
Where: i = Annual carrying charge rate, C = Unit cost of a towel to the store
Hence, H = 0.12 x S2.50H
= S0.30D is already given as 175 units per month, so the annual demand (D) will be:
D = 175 x 12D
= 2100 units per year
Substitute all values into the EOQ formula:
EOQ = √[(2 x 2100 x 375)/0.30]EOQ
= √[1,575,000]EOQ
= 1255.13 units
Rounding up, the optimal order quantity is 1256 units.
The minimum total cost will be calculated using the following formula:
TC = DH + (Q/2)S + (D/Q) x HC
Where: TC = Total cost H = Carrying cost per unit per year, S = Cost of placing an order, Q = Order quantity, D = Annual demand.
HC = Holding cost per unit per year
TC = (2100 x S2.50 x 0.3) + (1256/2 x S2.50) + (2100/1256 x 0.12 x S2.50)TC
= S 1575 + S1570 + S5.04TC
= S3150.04
Therefore, the optimal order quantity is 1256 units and the minimum total cost is S3150.04.
To know more about optimal order quantity, refer
https://brainly.com/question/29216697
#SPJ11
So I am rolling a standard dice once. Is rolling 3 or 4 mutually exclusive events? Please help me understand this.
Answers
what 2 numbers multiply to -63 and add to-2
Answers
=-63 and 7+-9 adds to -2
Two numbers are 7 and -9, so their product is -63 and sum is -2.
An equation is a mathematical statement that shows that two mathematical expressions are equal.
Let two numbers are x and y
Given,
The multiplication of 2 numbers is -63
\(x\times y =-63\)
The addition of 2 numbers is -2
\(x+y =-2\)
\(x=-2-y\)
On substituting x in \(x\times y =-63\)
\((-2-y)y=-63\)
\(-2y-y^2=-63\)
\(y^{2} +2y-63=0\)
\((y-7)(y+9)=0\)
\(y=7\\y=-9\)
\(x=-2-y\\\)
At y=7
x=-9
At x=-9
y=7
Thus, two numbers are 7 and -9
Learn more about equation, here:
https://brainly.com/question/29113090
#SPJ6
What i the um of the fraction? Ue the number 18 equivalent fraction to help find the anwer -3/41/2
Answers
fractions with the same denominator added together
You must add the numerators and keep the same denominator when adding fractions with the same denominator. Since the denominators of the two fractions are the same, we must add the numerators while maintaining the same denominator, which is 4.
What are the parts of fraction?
A fraction consists of two components. The numerator is the figure at the top of the line. It details the number of equal portions that were taken from the total or collection. The denominator is the figure that appears below the line.
The number below the bar is called the denominator . It tells the number of equal parts into which the whole has been divided. The number above the bar is called the numerator. It tells how many of the equal parts are being considered.
To learn more about fractions visit:
https://brainly.com/question/8482939
#SPJ4
If 74 amplifiers are sampled, what is the probability that the mean of the sample would differ from the population mean by greater than 2.8 watts
Answers
If 74 amplifiers are sampled, the probability that the mean of the sample would differ from the population mean by less than 2.8 watts is approximately 0.
The question is asking for the probability that the mean of the sample would differ from the population mean by less than 2.8 watts. We are given that the mean output of the amplifier population is 321 watts with a variance of 144, and that 74 amplifiers are sampled.
To find the probability, we can use the standard deviation, which is the square root of the variance. Therefore, the standard deviation is √144 = 12 watts.
Since we are dealing with a sample mean, we can use the formula for the standard error of the mean, which is the standard deviation divided by the square root of the sample size. In this case, the sample size is 74.
The standard error of the mean is 12 / √74 ≈ 1.3922 watts.
To find the probability that the mean of the sample would differ from the population mean by less than 2.8 watts, we can use the standard normal distribution. We can calculate the z-score using the formula: (x - μ) / σ, where x is the difference in means (2.8 watts), μ is the population mean (321 watts), and σ is the standard error of the mean (1.3922 watts).
The z-score is (2.8 - 321) / 1.3922 ≈ -231.0971.
To find the probability, we need to find the area under the standard normal curve to the left of the z-score. Using a standard normal table or a calculator, the probability is essentially 0 (rounded to four decimal places).
Therefore, the probability that the mean of the sample would differ from the population mean by less than 2.8 watts is approximately 0.
Complete Question: The mean output of a certain type of amplifier is 321 watts with a variance of 144. If 74 amplifiers are sampled, what is the probability that the mean of the sample would differ from the population mean by less than 2.8 watts? Round your answer to four decimal places.
To know more about probability refer here:
https://brainly.com/question/30249809
#SPJ11
According to data from an aerospace company, the 757 airliner carries 200 passengers and has doors with a mean height of 1.83 cm. Assume for a certain population of men we have a mean of 1.75 cm and a standard deviation of 7.1 cm. a. What mean doorway height would allow 95 percent of men to enter the aircraft without bending? 1.75x0.95 1.6625 cm b. Assume that half of the 200 passengers are men. What mean doorway height satisfies the condition that there is a 0.95 probability that this height is greater than the mean height of 100 men? For engineers designing the 757, which result is more relevant: the height from part (a) or part (b)? Why?
Answers
Based on the normal distribution table, the probability corresponding to the z score is 0.8577
Since the heights of men are normally distributed, we will apply the formula for normal distribution which is expressed as
z = (x - u)/s
Where x is the height of men
u = mean height
s = standard deviation
From the information we have;
u = 1.75 cm
s = 7.1 cm
We need to find the probability that the mean height of 1.83 cm is less than 7.1 inches.
Thus It is expressed as
P(x < 7.1 )
For x = 7.1
z = (7.1 - 1.75 )/1.83 = 1.07
Based on the normal distribution table, the probability corresponding to the z score is 0.8577
P(x < 7.1 ) = 0.8577
Read more about P-value from z-scores at; brainly.com/question/25638875
#SPJ4
The graph of g(x) is a transformation of the graph of f(x)=2x. Enter the equation for g(x) in the box. g(x) =

Answers
The -3 is not in the exponent
Explanation:
The parent function is \(f(x) = 2^x\). Plugging in x = 0 leads to y = 1. So the point (0,1) is on the f(x) curve. Going from (0,1) to (0,-2) is a vertical shift of 3 units downward. To represent this shift, we tack on a "-3" at the end of the f(x) function.
\(g(x) = f(x) - 3\\\\g(x) = 2^x - 3\)
You could look at other points as well, but I find working with x = 0 is easiest.
As a check, plugging x = 0 into g(x) leads to...
\(g(x) = 2^x - 3\\\\g(0) = 2^0 - 3\\\\g(0) = 1 - 3\\\\g(0) = -2\)
This confirms our answer.
Carlos is taking a car trip that is more than 240 miles, depending on the route he chooses. He has already driven 135 miles. How much farther does he have to go ?
Answers
Carlos have to travel 105 miles to reach the destination.
The path followed by an object to travel a predetermined distance at a predetermined speed from one place to another is called the distance traveled. As was previously said, the distance formula combines distance, speed, and time.
As per the details share in the above question are as bellow,
The details provided are as follow,
Carlos is traveling by automobile for more than 240 miles.
Carlos has traveled 135 miles so far.
How far must Carlos still travel?
We have to use subtraction method to determine the distance remaining.
Now subtract the total distance by the distance traveled,
Substitute the value in above we get,
=240-135
=105 miles
To know more about distance visit :
https://brainly.com/question/2854969
#SPJ4
given this array: 1 2 4 5 6 7 8 12 14 21 22 42 53 how many comparisons are required to find 42 using the binary search?
Answers
A total of 3 comparisons are required to find 42 using binary search in this particular array.
In binary search, the number of comparisons required to find a target value depends on the size of the array and the position of the target value within the array.
In this case, we have an array with 13 elements. In the first comparison, we compare the target value (42) with the middle element of the array.
The first comparison: 42 is compared with the middle element 8.
Since 42 is greater than 8, we can eliminate the first half of the array and continue the search in the second half. Now we have an array with 6 elements.
The second comparison: 42 is compared with the middle element 21.
Since 42 is greater than 21, we can again eliminate the first half of the remaining array and continue the search in the second half. Now we have an array with 3 elements.
The third comparison: 42 is compared with the middle element 42.
We have found the target value in the third comparison.
Know more about binary search here:
https://brainly.com/question/31605257
#SPJ11