Solve the initial value problem given by the differential equation: C1C2R2(Rc+R1)dt2d2qc2+[(Rc+R1)(C1+C2)+R2C2]dtdqc2+qc2=C2E and the initial conditions: qc2(0)dtdqc2(0)=0=0 Hereafter we will use the following values of the resistors, capacitances, and voltage: C1=10μFC2=100μFR1=100ΩR2=100ΩRc=1kΩE=5 V
Answers
To solve the given initial value problem, we will substitute the provided values of resistors (R1, R2, Rc), capacitances (C1, C2), and voltage (E) into the differential equation. Then, we will apply the initial conditions to determine the specific solution for qc2(t) and its derivative.
The initial value problem is described by the following differential equation:
C1C2R2(Rc+R1)d²qc²/dt² + [(Rc+R1)(C1+C2) + R2C2]dqc²/dt + qc² = C2E
By substituting the given values into the equation, we obtain:
10μF * 100μF * 100Ω * (1kΩ + 100Ω)d²qc²/dt² + [(1kΩ + 100Ω)(10μF + 100μF) + 100Ω * 100μF]dqc²/dt + qc² = 100μF * 5V
Simplifying the equation with these values, we can solve for qc²(t) by applying the initial conditions qc²(0) = 0 and dqc²/dt(0) = 0. The specific solution for qc²(t) will depend on the specific values obtained from the calculations.
Learn more about resistors here:
https://brainly.com/question/30672175
#SPJ11
Related Questions
Simplify 5a + 6 – 2a + 4
Answers
Answer:
3a+10
Step-by-step explanation:
3a+6+4
3a=10
5a-2a=3a+6+4
3a=10
SOLVE THIS PROBLEM ASAP PLS

Answers
Answer:
the answers are in the picture
Step-by-step explanation:

The General Social Survey asked 1676 people how many hours per day they were able to relax. The results are presented in the following table: 0 114 1 156 2 336 3 251 4 316 5 231 6 149
7 33
8 60
Total 1676 Consider these 1676 people to be a population. Let X be the number of hours of relaxation for person sampled at random from this population a) Construct the probability distribution of X. (3 marks) b) Find the probability that a person relaxes more than 4 hours per day. (2 marks) c) Find the probability that a person relaxes from 2 to 6 hours per day d) Find the probability that a person does not relax at all (2 marks) e) Compute the mean Mx. (3 marks) f) Compute the standard deviation Ox: (3 marks)
Answers
The probability distribution of the number of hours per day people are able to relax is constructed, and probabilities of relaxing more than 4 hours, between 2 to 6 hours, and not relaxing at all are 0.283, 0.767 and 0.068 respectively. The mean and standard deviation are 3.326 hours and 1.950 hours (approx.) respectively.
The probability distribution of X is:
X Frequency Probability
0 114 0.068
1 156 0.093
2 336 0.201
3 251 0.150
4 316 0.189
5 231 0.138
6 149 0.089
7 33 0.020
8 60 0.036
1676 1.000
The probability that a person relaxes more than 4 hours per day is:
P(X > 4) = P(X = 5) + P(X = 6) + P(X = 7) + P(X = 8)
= 0.138 + 0.089 + 0.020 + 0.036
= 0.283
The probability that a person relaxes from 2 to 6 hours per day is:
P(2 ≤ X ≤ 6) = P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6)
= 0.201 + 0.150 + 0.189 + 0.138 + 0.089
= 0.767
The probability that a person does not relax at all is:
P(X = 0) = 0.068
The mean Mx is:
Mx = Σ(X * P(X))
= 00.068 + 10.093 + 20.201 + 30.150 + 40.189 + 50.138 + 60.089 + 70.020 + 8*0.036
= 3.326 hours
The standard deviation Ox is:
Ox = sqrt[Σ(X^2 * P(X)) - Mx^2]
= sqrt[(0^20.068)+(1^20.093)+(2^20.201)+(3^20.150)+(4^20.189)+(5^20.138)+(6^20.089)+(7^20.020)+(8^2*0.036) - 3.326^2]
= 1.950 hours (approx.)
To know more about standard deviation:
https://brainly.com/question/23907081
#SPJ4
if two secants of a circle are ____ then they cut off congruent arcs
Answers
Answer: Parallel
Step-by-step explanation:
if two secanys of a circle are made them they cut off congruent arcs
Explain how u can decide where to place the first digit of the answer for 6,139 / 153
Answers
Answer:
The first digit would go in the tens place.
Step-by-step explanation:
First we estimate the approximate numbers. For 6130 we estimate 6000 and for 153 we estimate almost 150.
So dividing 6000 by 150 would give 40 .
The four would go in the ten's place .
Now check by dividing
40.1 So the answer is correct. The quotient is 40.12.
\(153\sqrt{6139}\)
612
190
153
37
The first digit would go in the tens place.
The answer is justified. We can easily decide where to place the first digit.
Step-by-step explanation:
explain how you can decide where to place the first diget in the quotiont for 6,139÷135
in attributes sampling, what effect does an increase in the acceptable risk of assessing control risk too low have on sample size?
Answers
Reduced sample size is a result of a fall in predicted rate, an increase in the tolerated rate, and a rise in the allowable risk of estimating control risk too low.
Given that,
We have to find what impact does a larger acceptable risk of estimating control risk too low have on sample size in characteristics sampling.
The term "risk of over-reliance" refers to the "risk of estimating control risk too low" in characteristics sampling, and it relates with the so-called
Reduced sample size is a result of a fall in predicted rate, an increase in the tolerated rate, and a rise in the allowable risk of estimating control risk too low.
To learn more about size visit: https://brainly.com/question/2292318
#SPJ4
6. Write a 2nd order homogeneous (not the substitution meaning for homogeneous here - how we used it for 2nd order equations) ODE that would result it the following solution: y = C₁+C₂e¹ (4pt)
Answers
The second-order homogeneous ordinary differential equation that corresponds to the given solution y = C₁ + C₂e^t is y'' + (a + 1)y' = 0.
A second-order homogeneous ordinary differential equation (ODE) is of the form:
y'' + ay' + by = 0,
where y'' represents the second derivative of y with respect to the independent variable, a and b are constants, and y is the dependent variable.
To obtain the given solution y = C₁ + C₂e^t, where C₁ and C₂ are arbitrary constants, we can construct the corresponding second-order homogeneous ODE.
Since y = C₁ + C₂e^t, taking the first and second derivatives of y, we have:
y' = 0 + C₂e^t = C₂e^t,
y'' = 0 + C₂e^t = C₂e^t.
Substituting these derivatives into the general form of the second-order homogeneous ODE, we get:
C₂e^t + a(C₂e^t) + b(C₁ + C₂e^t) = 0.
Simplifying this equation, we have:
C₂e^t + aC₂e^t + bC₁ + bC₂e^t = 0.
We can collect the terms with the same exponential factors:
(1 + a + bC₂)e^t + bC₁ = 0.
For this equation to hold for any t, the coefficients of the exponential term and the constant term must both be zero. Therefore, we have:
1 + a + bC₂ = 0,
bC₁ = 0.
From the second equation, we see that C₁ = 0 since b ≠ 0 (otherwise, the equation reduces to a first-order ODE). Substituting C₁ = 0 into the first equation, we get:
1 + a = 0.
Hence, the second-order homogeneous ODE that results in the given solution y = C₁ + C₂e^t is:
y'' + (a + 1)y' = 0.
To learn more about "derivative " refer here:
https://brainly.com/question/12047216
#SPJ11
Which inequality describes this graph?
A number line with arrows at both extends from less than negative 5 to past positive 5. A heavy arrow extends from a circle over positive 4 to the right.
Answers
The inequality that describes this graph of the number line is x ≥ 4
How to determine the inequality that describes this graph?From the question, we have the following properties:
The graph is a number lineThe number line extends at both endsThe number line starts from less than -5 and ends at greater than 5There is a heavy arrow that extends from a circle over positive 4 to the right.The property 3 above implies that the domain of the number line is the set of all real numbers.
The property 4 above implies that the inequality of the number line is a greater than or equal to inequality, and the value starts from 4
This is represented by the following inequality
x ≥ 4
Hence, the inequality that describes this graph of the number line is x ≥ 4
Read more about number line at
https://brainly.com/question/24644930
#SPJ1
not yet answered points out of 5.00 not flaggedflag question question text let s be the set of the 2005 smallest positive multiples of 4, and let t be the set of the 2005 smallest positive multiples of 6. how many elements are common to s and t?
Answers
The number of elements common to sets S and T, where S is the set of the 2005 smallest positive multiples of 4 and T is the set of the 2005 smallest positive multiples of 6, can be determined by finding the least common multiple (LCM) of 4 and 6 and dividing it by 4.
The multiples of 4 can be written as {4, 8, 12, 16, ...}, while the multiples of 6 can be written as {6, 12, 18, 24, ...}. To find the common elements, we need to determine the numbers that are divisible by both 4 and 6.
The LCM of 4 and 6 is 12. To find the number of elements common to sets S and T, we divide the LCM (12) by 4 since the sets consist of the smallest positive multiples. This gives us 12/4 = 3.
Therefore, there are 3 elements that are common to both sets S and T.
Learn more about sets here:
https://brainly.com/question/31447621
#SPJ11
Dilate triangle ABC using center P and scale factor 32
Answers
To dilate triangle ABC using center P and a scale factor of 32, we can apply the following steps. Firstly, locate the center of dilation, P, which will be the reference point for the dilation. Then, for each vertex of the original triangle, draw a line segment from the vertex to point P. Finally, multiply the length of each line segment by the scale factor of 32 to determine the corresponding points on the dilated triangle.
In summary, to dilate triangle ABC with center P and a scale factor of 32, we locate the center of dilation, draw line segments from each vertex to point P, and multiply the length of each line segment by the scale factor of 32 to find the corresponding points on the dilated triangle.
The center of dilation, P, serves as the reference point for the dilation. It acts as the anchor around which the triangle expands or contracts. To dilate each vertex, we draw a line segment from the original vertex to point P. This line segment represents the direction and distance of the dilation. By multiplying the length of each line segment by the scale factor of 32, we determine the new positions of the vertices on the dilated triangle. The scale factor of 32 indicates that the dilated triangle will be enlarged by a factor of 32, resulting in a significant increase in size compared to the original triangle.
To learn more about Vertex - brainly.com/question/32432204
#SPJ11
What is 10000+2739 =?
Answers
Answer:
102739
Step-by-step explanation:
Answer:
12739
Step-by-step explanation:
10000 + 2739 = 12739
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
write the equation of an exponential function that passes through the points (2,48) and (5,750).
Answers
Substitute in the values:
750 = a * b5
and
48 = a * b2
Then divide the two equations:
750/ 48 = (a * b5) / (a * b2)
So:
15.625 = b3
Take the cube root of both sides:
2.5 = b
Now, substitue b into one of the equations (the one with 48 has smaller numbers and is easier to work with.)
48 = a * 2.52
Simplify.
48 = a * 6.25
Divide both sides by 6.25
7.68 = a
Now substitute in a and b to write the exponential function:
y = 7.68 * 2.5x
The equation of an exponential function will be y = 7.68 × 2.5ˣ.
What is equation of line?
The equation of line with slope m and passes through the point (x₁, y₁) is calculated as;
y - y₁ = m (x - x₁)
Given that;
An exponential function passes through the points (2, 48) and (5, 750).
Now, The exponential function is;
y = abˣ
Where, a and b are unknowns.
Hence, For the point (2, 48), we get the equation;
48 = ab² .. (i)
And, For the point (5, 750), we get;
750 = ab⁵ .... (ii)
Solve the equation (i) for value of a, we get;
48 = ab²
a = 48/b²
Substitute in equation (ii);
750 = ab⁵
750 = (48/b²) b⁵
750 = 48 b³
b³ = 750/48
Take cube root both side;
b = 5/2
Hence, a = 48/b² = 48/(5/2)²
a = 48 × 4 / 25
a = 7.68
Thus, After substitute the value of a and b we get the exponential equation as;
y = 7.68 × 2.5ˣ
Therefore, The equation of an exponential function will be,
⇒ y = 7.68 × 2.5ˣ.
Learn more about the exponential function visit:
https://brainly.com/question/26039564
#SPJ2
find the area of the shaded region.
pls do this with explanation.

Answers
Answer:
first find the area of the big rectangle = 12×14=168
area of the small unshaded rectangle =2×5×6=60
area of the shaded region = 168-60=108
ANSWER
My answer is in the photos above


Last one I promise . I am NOT GOOD AT MATH
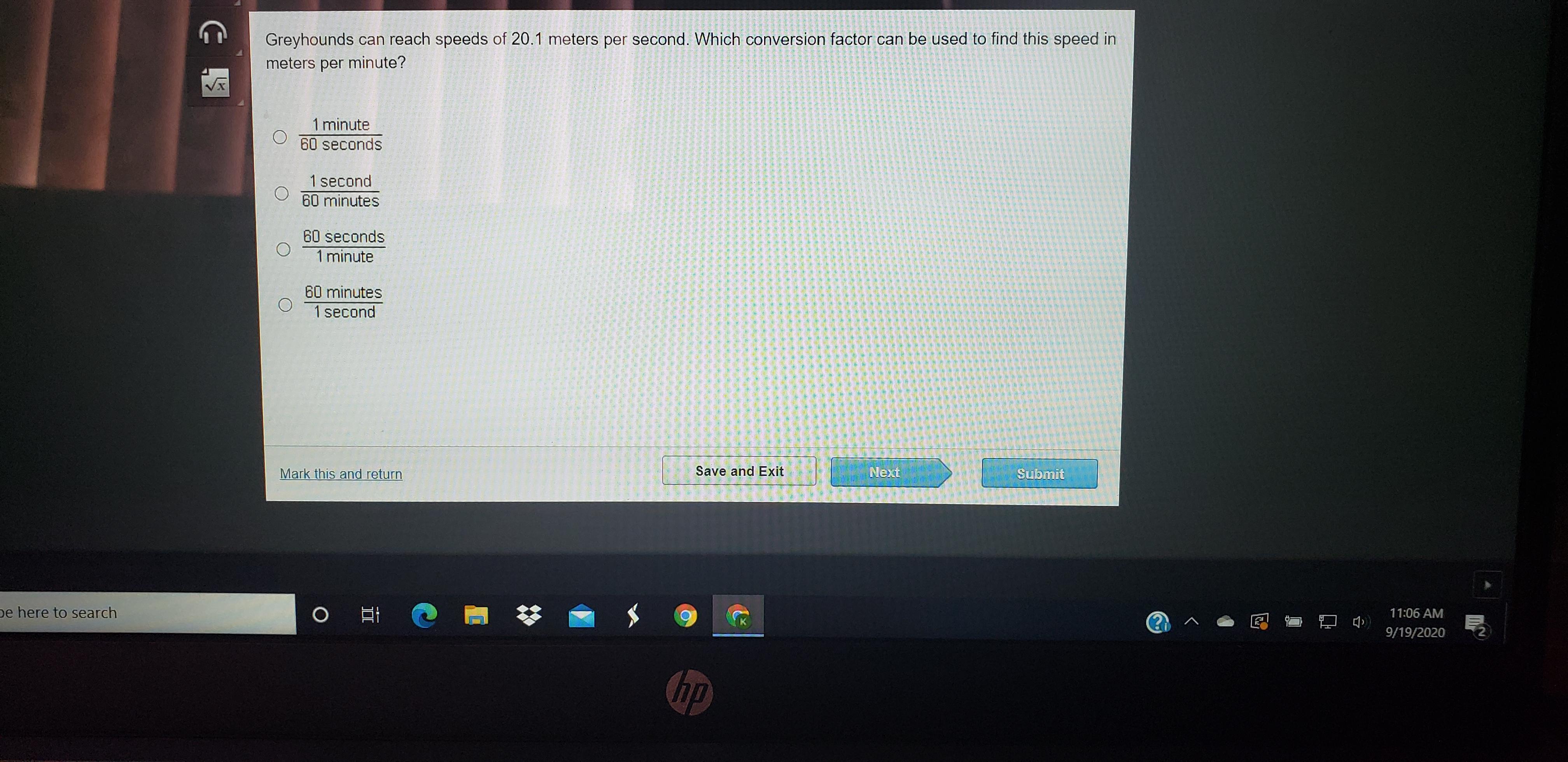
Answers
Answer:
60 seconds/1 minute
Step-by-step explanation:
We are trying to convert 20.1 meters/second to per minute. Since we know there's 60 seconds in a minute, we would use the conversion factor 60 seconds/1 minute in order to find greyhounds speed per minute
x - 2 ⪯ 5 solve plz..
Answers
Answer:
x ⪯ 7
Step-by-step explanation:
5 + 2 = 7
Express ********** using a number in each given system.
a) base four
b) base five
c) base eight
Answers
The expression ********** can be represented as 3333333333 in base four, 4444444444 in base five, and 7777777777 in base eight, according to the respective numerical systems.
a) In base four, each digit can have values from 0 to 3. The symbol "*" represents the value 3. Therefore, when we have ten "*", we can express it as 3333333333 in base four.
b) In base five, each digit can have values from 0 to 4. The symbol "*" represents the value 4. Hence, when we have ten "*", we can represent it as 4444444444 in base five.
c) In base eight, each digit can have values from 0 to 7. The symbol "*" represents the value 7. Thus, when we have ten "*", we can denote it as 7777777777 in base eight.
To know more about expression, visit:
https://brainly.com/question/28170201#
#SPJ11
4/5 n = 1 - 1/5 n
solve for n:
please help
Answers
Answer:
3/2 = 1/ 1/2
Step-by-step explanation:
1 1/5 divided by 4/5 is 1 1/2
Answer:
1
Step-by-step explanation:
4/5n=1-1/5n
so we collect the like terms
4/5n+1/5n=1
n=1
BIG IDLAS MATH
#19 i
Evaluate the expression. Write your answer in scientific notation.
(6 x 10-3) + 0.23 – (5 x 10-2) =
Answers
Answer:
Step-by-step explanation:
9.23
PLEASE HELP ITS DUE IN 10 MINUTES IF YOU PUT A LINK I WILL REPORT YOU AND I WILL GIVE BRAINLIEST

Answers
Answer:
|x + 7| ≥ 2 is the inequality
Step-by-step explanation:
x - b ≥ c or x - b ≤ -c
x ≥ b + c = -5 or x ≤ b - c = -9
b + c = -5
b - c = -9
2b = -14
b = -7 -7 + c = -5
c = 2
x - (-7) = x + 7
So, |x + 7| ≥ 2 is the inequality
Segment AB has endpoints A(5, 2) and B(9, 10) that is divided by a point C such that AC and BC form a 2:3 ratio. The distance between the x-coordinates is 4 units. Which of the following fractions represent how far C is on the pathway from A to B? (6 points)
3 over 5
3 over 2
2 over 3
2 over 5
Answers
The answer is D. 2 over 5
Step-by-step explanation:
Took the test.
find the maximum and minimum values of the function f ( x , y ) = e^xy subject to x^3 + y^3 = 54
Answers
The maximum value of f(x,y) is e^27, and the minimum value of f(x,y) is approximately 203.64.
The method of Lagrange multipliers can be used to find the maximum and minimum values of f(x, y) subject to the constraint x^3 + y^3 = 54.
Let g(x,y) = x^3 + y^3 - 54 be the constraint equation. We need to solve the system of equations:
grad(f) = λ grad(g)
g(x,y) = 0
where λ is the Lagrange multiplier.
Taking partial derivatives of f(x,y), we get:
fx = ye^xy = λ 3x^2
fy = xe^xy = λ 3y^2
Taking partial derivatives of g(x,y), we get:
gx = 3x^2 = 0
gy = 3y^2 = 0
Solving for x and y, we get:
x = y = (54/2)^(1/3) = 3∛18
The value of λ can be found by substituting the values of x and y into the equation grad(f) = λ grad(g):
ye^xy = λ 3x^2
xe^xy = λ 3y^2
Substituting x = y = 3∛18, we get:
λ = e^(18) / (9∛2)
To find the maximum and minimum values of f(x,y), we need to evaluate f(x,y) at the critical point (x,y) = (3∛18, 3∛18) and at the endpoints of the constraint region. The constraint x^3 + y^3 = 54 is satisfied on the boundary of the region, which is a compact set, so we can apply the extreme value theorem.
At the critical point, we have:
f(3∛18, 3∛18) = e^(54/2) = e^27
On the boundary of the region, we have:
f(x,y) = e^xy = e^(54-x^3) at y = (54-x^3)^(1/3)
Taking the derivative with respect to x, we get:
f'(x) = -3x^2 e^(54-x^3) + ye^(54-x^3) = 0
Substituting y = (54-x^3)^(1/3), we get:
-3x^2 e^(54-x^3) + (54-x^3)^(1/3) e^(54-x^3) = 0
Solving numerically, we get:
x = 2.8964, y = 3.8406 or x = 3.8406, y = 2.8964
At these points, we have:
f(2.8964, 3.8406) ≈ 203.64
f(3.8406, 2.8964) ≈ 203.64
Therefore, the maximum value of f(x,y) is e^27, and the minimum value of f(x,y) is approximately 203.64.
Learn more about maximum value here
https://brainly.com/question/30096512
#SPJ11
In a polynomial equation, the sum of the multiplicities of the roots always add up to.
Answers
The sum of the multiplicities of the roots in a polynomial equation is equal to the degree of the polynomial (the highest power of the variable in the equation).
This is known as the Fundamental Theorem of Algebra. The multiplicity of a root is the number of times a root appears in a polynomial equation, and it can be a whole number, a fraction, or even an irrational number.
For example, if the polynomial equation is x³ + 2x² + 4x - 8 = 0, then the degree of the polynomial is 3 and the multiplicities of the roots are 1, 2, and 1, respectively.
Therefore, the sum of the multiplicities of the roots in this equation is 3. This is true for any polynomial equation: the sum of the multiplicities of the roots will always be equal to the degree of the polynomial.
Learn more about polynomial equation:
https://brainly.com/question/29513223
#SPJ4
Mica is making a paste for an art project. He mixes 8 cups of water with glue. If he wants to make a double batch how many quarts of water does he need?how much water is that in gallons?
Answers
He needs one more quart. That is half of a gallon.
Can you help me with this I really need it it is for a test

Answers
Answer:
90
Step-by-step explanation:
each dot = 45 bc 540 / how many dots there are which is 12 = 45 then there are 2 dots worth of 45 making it 90
math
540/12=45
45 x 2 = 90
Answer: 135 students
Step-by-step explanation:
1. Divide 540 (total number of students) by the number of dots (12)
2. So then 540/12= 45
3. Then see how many dots are more then 5 miles away so that is 3 dots (2dots on 6 miles, and 1 dot on 7 miles)
4. After 45*3= 135
Given the curve that satisfies the relationship: x * sin(2y) = y * cos(2x)
Determine the equation of the tangent at (pie/4, pie/2)
Answers
To find the equation of the tangent at the point (π/4, π/2) on the curve given by x * sin(2y) = y * cos(2x), we need to find the slope of the tangent at that point.
First, we find the derivative of the given curve with respect to x using the product rule and the chain rule:
d/dx [x * sin(2y)] = d/dx [y * cos(2x)]
sin(2y) + x * 2cos(2y) * dy/dx = cos(2x) - y * 2sin(2x) * dx/dy
At the point (π/4, π/2), we substitute x = π/4 and y = π/2 into the above equation. Also, since the slope of the tangent is dy/dx, we solve for dy/dx:
sin(π) + (π/4) * 2cos(π) * dy/dx = cos(π/2) - (π/2) * 2sin(π/2) * dx/dy
1 + (π/2) * (-2) * dy/dx = 0 - (π/4)
1 - π * dy/dx = -π/4
dy/dx = (1 - π/4) / (-π)
Finally, we have the slope of the tangent dy/dx = (1 - π/4) / (-π).
Using the point-slope form of a line, we can write the equation of the tangent as:
y - (π/2) = [(1 - π/4) / (-π)] * (x - π/4)
Simplifying this equation gives the final equation of the tangent at (π/4, π/2) on the given curve.
Learn more about tangent here: brainly.com/question/32386532
#SPJ11
15 - 2x = -7x
How do you solve this? Plz show step-by-step if possible no picture. Thank you! :)
Answers
Answer:
= − 3
Step-by-step explanation:
15−2x=−7x
− 2 + 15 = −7
−2+15−15=−7−15
−2=−7−15
so 1 . you rearrange the terms
2. subtract 15 from both sides
3 simpfly subtract the number
Answer:
You will move - 2x to the other side to gather factores x with considering change the sign because the changing in side so it will became
15=2x-7x
15=-5x
To find x you need to remove its variable -5 and that happen by devided it just basic algebra
X=15/-5
X=-3
a kite flying in the air has a 94- string attached to it, and the string is pulled taut. the angle of elevation of the kite is . find the height of the kite. round your answer to the nearest tenth.
Answers
The height of the kite is approximately 68.4 ft.
To solve the problem, we can use trigonometry. We know that the string is the hypotenuse of a right triangle, with the height of the kite as one of the legs. The angle of elevation, which is the angle between the string and the ground, is also given. We can use the tangent function to find the height of the kite:
tan(46°) = height / 94
Solving for height, we get:
height = 94 * tan(46°)
Using a calculator, we get:
height ≈ 68.4 ft
Therefore, the height of the kite is approximately 68.4 ft.
We use the given angle of elevation and the length of the string to set up a right triangle with the height of the kite as one of the legs. Then, we use the tangent function to relate the angle to the height of the kite. Finally, we solve for the height using a calculator and round to the nearest tenth as requested.
Learn more about the height
https://brainly.com/question/28122539
#SPJ4
Complete Question:
A kite flying in the air has a 94-ft string attached to it, and the string is pulled taut. The angle of elevation of the kite is 46 °. Find the height of the kite. Round your answer to the nearest tenth.
The table below represents a breakdown of food costs for Eddie, a traveling
salesman. How much did he spend in total for food on Tuesday?
Mon.
Tue.
Wed.
Thurs.
Fri.
Breakfast $7.88
$12.02
$9.64
$6.98
$13.30
Lunch
$13.41
$11.79
$14.55
$16.09
$10.76
Dinner
$18.80
$22.13
$20.79
$24.82
$16.74
OA. $40.09
OB. $42.56
OC. $41.23
OD. $45.94
SURMIT
Answers
The total amount of money that was spent on lunch on Tuesday is $45.94.
What is the total amount spent on food?
The total amount that was spent on food on Tuesday can be determined by adding the amount spent on breakfast, lunch and dinner. Addition is the mathematical operation that is used to determine the sum of two or more numbers.
Total amount spent = 22.13 + 12.02 + 11.79 = $45.94
To learn more about addition, please check: https://brainly.com/question/349488
#SPJ1
Which list of numbers can be described by the following rule?
A. 33,49,67
B.65,49,33
C.33,49,65
D.65,48,33

Answers
Explanation:
first term = 33
second term = first term + 16 = 33+16 = 49
third term = second term + 16 = 49+16 = 65
We're adding 16 to each term to get the next term.
Answer:
c is correct
mark as brainiest please
Kevin makes muffins. It takes 8 minutes to mix the batter. The muffins bake for 17 minutes. The muffins then cool for 5 minutes. What is the total amount of time, in minutes, Kevin spends mixing, baking, and cooling the muffins? Enter your answer in the box. minutes
Answers
Answer: THE TOTAL AMOUNT TAKEN BY KEVIN IN MIXING, BAKING, AND COOLING THE MUFFINS IS 30 MINUTES.
Step-by-step explanation:
1. AMOUNT TAKEN BY KEVIN FOR MIXING=8MIN.
2. AMOUNT TAKEN BY KEVIN FOR BAKING=17 MIN.
3. AMOUNT TAKEN BY KEVIN FOR COOLING=5MIN.
IN TOTAL, (8+17+5)MIN. = 30 MIN.
Answer:
30 minutes
Step-by-step explanation:
8+7 =15 +5=20+ another 10 = 30