Solve the inequality. Apply properties
Add
Subtract
Multiply
Divide
1/2-1/4x ≥ -1/4
Answers
Answer:
x \(\leq\) 3
Step-by-step explanation:
\(\frac{1}{2}\) - \(\frac{1}{4}\)x \(\geq\) - \(\frac{1}{4}\)
the first step is to subtract \(\frac{1}{2}\) from both sides of the equation.
\(\frac{1}{2}\) - \(\frac{1}{4}\)x \(\geq\) - \(\frac{1}{4}\)
-\(\frac{1}{2}\) - \(\frac{1}{2}\)
----------------
-\(\frac{1}{4}\)x \(\geq\) - \(\frac{3}{4}\)
then, divide both sides of the equation by - \(\frac{1}{4}\).
x \(\leq\) 3
(since we divided both sides by a negative number, to isolate x, the \(\geq\) changed to \(\leq\).)
Answer:
1/2 - 1/4x ≥ -1/4
multiply both sides by the l.c.m of the both sides(4)
4(1/2 - 1/4x )≥ -1/4 ×4
2 - x ≥ -1
Collect the like terms
-x ≥ -3
Divide both sides by -1
x ≤ 3(when you divide by a negative number the equality changes)
Related Questions
Name the geometric term modeled by the given object.
a blanket
Answers
The geometric term modeled by a blanket is a rectangular prism. A rectangular prism is a solid three-dimensional object which has six faces where each face is a rectangle.
A blanket is flat, which implies that it has a length and width but no height. However, after being folded and stacked, it will take up the shape of a rectangular prism, as it occupies some volume. The rectangular prism is also known as a cuboid or a box, which can be used interchangeably. It is a type of polyhedron that has six rectangular faces that are connected by rectangular sides and edges. The rectangular prism has two types of sides which are the lateral faces (or lateral surfaces) and the base faces (or base surfaces). The lateral faces of a rectangular prism are all the same, and the base faces are also identical to each other. All lateral edges and base edges of the rectangular prism are perpendicular to the other edges.
Know more about rectangular prism, here:
https://brainly.com/question/27812749
#SPJ11
Please help ASAP! Only answer if you know the correct answer! Thanks :)

Answers
Plsss help correct answer gets marked

Answers
Answer:
B
Step-by-step explanation:
there are 7 blocks in the whole
the green portion is 3/7
1/2 times 6/7 is equal to 3/7
the answer is B
What are the coordinates of the midpoint segment joining the points A(-3,-4) and B(4,2)
Answers
Answer:
Step-by-step explanation:
x1 + x2 divided by 2
y1 + y2 divided by 2
-3 + 4 is 1/2
-4 + 4 is 0
(0.5,0)
i could be wrong but i did it in my head , but the equation is right . just do that in order
Answer:
( 0.5, - 1 )
Step-by-step explanation:
So here is the equation:
x2 + x1 / 2 For the x coordinate
y2 + y1 / 2 For the y coordinate
x2 is 4 and x 1 is -3 whilst y2 is 2 and y1 is -4.
Thus:
4 + -3 / 2 = 0.5 x coordinate
2 + -4 / 2 = -1 y coordinate
So it becomes (0.5, -1)
HOPE THIS HELPED
if (-2/15)+(-13/5)=(-13/5)+a/b then a/b is equal to

Answers
The choose C. –2/15
(-2/15) +(-13/5) =(-13/5) +a/b
a/b = (-2/15)+(-13/5) - (-13/5)
a/b = (-2/15) - ( 39/15) +(39/15)
a/b = –2/15
I hope I helped you ^_^
Answer: option 3: a/b = (-2/15)
Step-by-step explanation:
See here when we solve this
(-2/15)+(-13/5) = (-13/5)+a/b
(-2/15) = (-13/5)+a/b-(-3/15)
(-2/15) = a/b
please click thanks and mark brainliest if you like :)
Find A and B. Using the image above.

Answers
Answer:
a = 7, b = \(\frac{7\sqrt{3} }{3}\)
Step-by-step explanation:
Using the sine ratio in the left right triangle and the exact value
sin45° = \(\frac{1}{\sqrt{2} }\) , then
sin45° = \(\frac{opposite}{hypotenuse}\) = \(\frac{a}{7\sqrt{2} }\) = \(\frac{1}{\sqrt{2} }\) ( cross- multiply )
a × \(\sqrt{2}\) = 7\(\sqrt{2}\) ( divide both sides by \(\sqrt{2}\) )
a = 7
--------------------------------------------------------
Using the tangent ratio in the right triangle on the right and the exact value
tan60° = \(\sqrt{3}\) , then
tan60° = \(\frac{opposite}{adjacent}\) = \(\frac{a}{b}\) = \(\frac{7}{b}\) = \(\sqrt{3}\) ( multiply both sides by b )
b × \(\sqrt{3}\) = 7 ( divide both sides by \(\sqrt{3}\) )
b = \(\frac{7}{\sqrt{3} }\) × \(\frac{\sqrt{3} }{\sqrt{3} }\) = \(\frac{7\sqrt{3} }{3}\)
How much is 6 oz to a cup?
Answers
6 ounces is equal to 0.75 cups.
The conversion factor between ounces (oz) and cups is 1 cup = 8 ounces. To convert ounces to cups, divide the number of ounces by 8. For example, 6 ounces is equal to 6/8 = 0.75 cups.
It is important to note that measurements in cooking and baking can vary depending on the recipe and the level of precision required. However, using measuring cups and spoons is a good way to ensure that ingredients are added in the correct proportion.
Additionally, it is always good practice to check the recipe and make sure you are using the right measurement units. Additionally, it's worth noting that ounces and cups are both units of measurement used in cooking and baking, but they're not interchangeable,
so you should always use the right unit of measurement for the recipe you're following.
To know more about conversion factor on the link below:
brainly.com/question/30166433#
#SPJ11
Tickets to the amusement park cost 12 dollars for adults and 8 dollars for kids. WRITE an algebraic expression to show the cost of a adults and k kids
Answers
Tickets cost per adult = $12
Tickets cost per kid = $8
Total cost for a adults = 12a
Total cost for k kids = 8k
Algebraic expression to show cost for a adults and k kids = 12a + 8k dollars
Help please!
Sorry for the image quality.
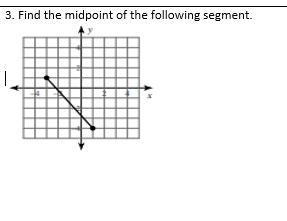
Answers
Answer:
\(\displaystyle (-1,\frac{-3}{2})\)
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Midpoint Formula: \(\displaystyle (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)Step-by-step explanation:
Step 1: Define
Find points from graph.
Point (-3, 1)
Point (1, -4)
Step 2: Find Midpoint
Simply plug in your coordinates into the midpoint formula to find midpoint
Substitute [MF]: \(\displaystyle (\frac{-3+1}{2},\frac{1-4}{2})\)[Fractions] Add/Subtract: \(\displaystyle (\frac{-2}{2},\frac{-3}{2})\)[Fractions] Divide: \(\displaystyle (-1,\frac{-3}{2})\)A box contains 18 red marbles and 18 green marbles. sampling at random from the box five times with replacement, you have drawn a red marble all five times. what is the probability of drawing a red marble the sixth time?
Answers
The probability of drawing a red marble is 0.5
What is Probability?Probability is a way to determine how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about how probable an event is to happen, or its chance of happening. Probability can range from 0 to 1, with 0 denoting an impossibility and 1 denoting a certainty.
Probability of an event=\(\frac{Number of Favourable outcomes}{Total number of outcomes}\)
In this problem, a single marble is drawn from a box of 36 marbles: 18 red and 18 green. We are told that five draws have to be done. The event is independent of the others. The probability of drawing a red marble will always be the same in this situation. Since every marble is equally likely to be drawn, the probability of drawing red is
P(R)=\(\frac{Number of Favourable outcomes}{Total number of outcomes}\)
Here the favorable outcome is number of red balls and the total number of outcomes is total number of balls
=18/(18+18)
=18/36
=1/2
=0.5
For more information on probability visit:
https://brainly.com/question/11234923
#SPJ4
3. A car originally cost $16,000. The owner reduced the price of the car by 20%. After a few
weeks, the owner reduced the price of the car by another 20%, Belinda then purchased the
If a 3% sales tax was added, how much did Belinda pay for the car?
A. $9,600.80
B. $9,888,20
C. $10,240.00
D. $10,547.20
Answers
Answer:
the answer is D: $10547.20
solve the following quadratic by factoring: 6x^2-12x=0
Answers
Answer:
X=0,-2
Step-by-step explanation:
6 x ( x + 2 ) = 0 Divide each term in 6 x ( x + 2 ) = 0 by 6 . 6 x ( x + 2 ) 6 = 0 6 Cancel the common factor of 6 . x ( x + 2 ) = 0 6 Divide 0 by 6 . x ( x + 2 ) = 0 If any individual factor on the left side of the equation is equal to 0 , the entire expression will be equal to 0 . x = 0 x + 2 = 0 Set the first factor equal to 0 . x = 0 Set the next factor equal to 0 and solve. Tap for more steps... x = − 2 The final solution is all the values that make 6 x ( x + 2 ) 6 = 0 6 true. x = 0 , − 2
Which equation represents circle C?

Answers
Answer:
The equation of the circle is
(x + 4)^2 + (y-1)^2 = 162
Step-by-step explanation:
Here, we want to give the correct equation of the circle.
The center of the circle is (-4,1)
Now the other parameter we need to show the equation of the circle is the radius of the circle and this can be obtained from the distance between the circle center and a point on the circumference.
We use the distance formula to calculate this.
So the distance we want to calculate is the distance between;
(-4,1) and (5,-8)
using the distance formula, we have
d = √(x2-x1)^2 + (y2-y1)^2
Substituting these values, we have;
d = √(5 + 4)^2 + (-8-1)^2
d = √(9^2 + 9^2)
d = √(162)
d = 9 √2 units
The formula for the equation of a circle is
(x-h)^2 + (y-k)^2 = r^2
where (h,k) are coordinates of the center which is (-4,1) in this question
The way of the circle is thus,
(x-(-4)^2 + (y-1)^2 = {9√(2)}^2
(x + 4)^2 + (y-1)^2 = 162
I’m trying to find x for length on a triangle that has 4 sides 6 total because 2 sides are together, I have only 3 sides those are, 5 mm, 13 mm, 35 mm, then x what is it?

Answers
Check the picture below.
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{13}\\ a=\stackrel{adjacent}{5}\\ o=\stackrel{opposite}{y} \end{cases} \\\\\\ y=\sqrt{ 13^2 - 5^2}\implies y=\sqrt{ 169 - 25 } \implies y=\sqrt{ 144 }\implies y=12 \\\\[-0.35em] ~\dotfill\)
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ c^2=a^2+o^2\implies c=\sqrt{a^2 + o^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{x}\\ a=\stackrel{adjacent}{35}\\ o=\stackrel{opposite}{12} \end{cases} \\\\\\ x=\sqrt{ 35^2 + 12^2}\implies x=\sqrt{ 1225 + 144 } \implies x=\sqrt{ 1369 }\implies \boxed{x=37}\)

Dan spends 1/5 of his wages on rent and 2/3 on food. If he makes £495 per week how much money does he have left
Answers
Answer:
£66
Step-by-step explanation:
1/5 times £495
2/3 times £495
Rent =£99
Food =£330
99+330=429
495-429=£66
I hope that help you and you learned how to do it for next time.
Answer:
£66 Left
Step-by-step explanation:
Total Money = £495
Rent:
=> \(\frac{1}{5} * 495\)
=> £99
Food:
=>\(\frac{2}{3} * 495\)
=> 2 * 165
=> £330
Left:
=> £495-£99-£330 = £66
find a power series representation for the function. f(x) = x^8 tan^−1(x^3)
Answers
The Power series representation of f(x) = \(x^8tan^-^1x^3\) is \($$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^6^n^+^1^1}{2n+1}\)
What is Maclaurin series?The Maclaurin series expansion method can be used to get the power series of such functions if the function has a composite part, such as the multiplication or quotient form.
What is power series?
An infinite series in mathematics known as a "power series" can be compared to a polynomial with an infinite number of terms.
The Maclaurin series will be used in this instance to expand the function:
\(tan^-^1x\) = \($$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^2^n^+^1}{2n+1}\)
and for \(tan^-^1x^3 = $$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{(x^3)^2^n^+^1}{2n+1}\)
=> \(tan^-^1x^3 = $$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^6^n^+^3}{2n+1}\) -------(i)
and f(x) = \(x^8tan^-^1x^3\)
now we need to multiply \(x^8\) in the above equation to get the power series expansion of f(x)
\(x^8tan^-^1x^3\) = \(x^8\) \($$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^6^n^+^3}{2n+1}\)
=> \($$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^6^n^+^3^+^8}{2n+1}\)
=> \($$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^6^n^+^1^1}{2n+1}\)
so the expansion of f(x) = \(x^8tan^-^1x^3\) is \($$ \Sigma_{n=0}^\infty $$ (-1)^n\frac{x^6^n^+^1^1}{2n+1}\)
To know more about Maclaurin series click on below link:
https://brainly.com/question/24188694#
#SPJ4
pls what is 2,504+140+160 plss
Answers
Answer:
2804
Step-by-step explanation:
2504 + 140 + 160 = 2804 (hint: add the 140 + 160 first. It sums up to 300 which is easy to add to 2504)
Solve the non-linear Differential Equation y"=-e" : y = f(x) by explicitly following these steps: (Note: u= f(y), w=f(u) so use the chain rule as necessary) i. (15 pts) Find a non-transcendental expression for the DE above, by letting u = e, and then rewriting it wrt u
Answers
The non-transcendental expression for the differential equation y" = -e" by letting u = e and rewriting it with respect to u is du/dy * (-e") + (du/dy * y')² = -e".
To solve the non-linear differential equation y" = -e", we can follow the given steps:
Step i: Find a non-transcendental expression for the differential equation by letting u = e and then rewriting it with respect to u.
Let's start by finding the derivatives of u with respect to x:
du/dx = du/dy * dy/dx [Using the chain rule]
= du/dy * y' [Since y' = dy/dx]
Taking the second derivative:
d²u/dx² = d(du/dx)/dy * dy/dx
= d(du/dy * y')/dy * y' [Using the chain rule]
= du/dy * y" + (d(du/dy)/dy * y')² [Product rule]
Since we are given the differential equation y" = -e", we substitute this into the above expression:
d²u/dx² = du/dy * (-e") + (d(du/dy)/dy * y')²
= du/dy * (-e") + (du/dy * y')² [Since y" = -e"]
Now, we can rewrite the differential equation with respect to u:
du/dy * (-e") + (du/dy * y')²
= -e"
This gives us the non-transcendental expression for the differential equation in terms of u.
To know more about differential equation,
https://brainly.com/question/32663870
#SPJ11
Exercise 5-39 Algo Let X represent a binomial random variable with n-320 and p-076. Find the following probabies. (Do not round Intermediate calculations. Round your final answers to 4 decimal places)
Answers
Therefore, P (X = 266 or X = 274) ≈ 0.0000017686 + 0.000000000006114 ≈ 0.0000017686.
Exercise 5-39 Algo Let X represent a binomial random variable with n = 320 and p = 0.76.
The problem is to determine the following probabilities. P(X > 255)P(X ≤ 254)P(266 ≤ X ≤ 274)P(X = 266 or X = 274) Solution P(X > 255)
The probability that the random variable X is greater than 255 is given by; P(X > 255) = 1 - P(X ≤ 255)Therefore, using the normal approximation to the binomial distribution, we have; μ = np = 320(0.76) = 243.2σ = √(np(1-p)) = √(320(0.76)(0.24)) ≈ 8.2266
The continuity correction factor will be used to obtain the value of the standard normal variable to use for the calculation. Z = (255 + 0.5 - μ)/σ = (255.5 - 243.2)/8.2266 ≈ 1.4981Using the standard normal table, we have;P(Z > 1.4981) ≈ 1 - 0.9337 ≈ 0.0663
Therefore, P(X > 255) ≈ 0.0663.P(X ≤ 254) Similarly, using the normal approximation to the binomial distribution; μ = np = 320(0.76) = 243.2σ = √(np(1-p)) = √(320(0.76)(0.24)) ≈ 8.2266Z = (254 + 0.5 - μ)/σ = (254.5 - 243.2)/8.2266 ≈ 1.3736Using the standard normal table,
we have;P(Z ≤ 1.3736) ≈ 0.9149Therefore, P(X ≤ 254) ≈ 0.9149.P(266 ≤ X ≤ 274)Using the normal approximation to the binomial distribution; μ = np = 320(0.76) = 243.2σ = √(np(1-p)) = √(320(0.76)(0.24)) ≈ 8.2266Z₁ = (266 + 0.5 - μ)/σ = (266.5 - 243.2)/8.2266 ≈ 2.8259Z₂ = (274 + 0.5 - μ)/σ = (274.5 - 243.2)/8.2266 ≈ 3.7913
Therefore; P(266 ≤ X ≤ 274) ≈ P(2.8259 ≤ Z ≤ 3.7913) ≈ P(Z ≤ 3.7913) - P(Z ≤ 2.8259) ≈ 0.0029P(X = 266 or X = 274)Since X is a discrete random variable,
we have; P(X = 266 or X = 274) = P(X = 266) + P(X = 274) Using the binomial distribution, we have;P(X = 266) = C(320,266)p^266(1-p) ^(320-266) ≈ 0.0000017686P(X = 274) = C(320,274)p^274(1-p)^(320-274) ≈ 0.000000000006114
To know more about binomial distribution, visit:
https://brainly.com/question/29137961
#SPJ11
Phillip wants to buy a baseball cap. Sales tax in his city is 8%.
Select the prices of all caps Phillip could buy for less than or equal
to $20 once sales tax is added.
Answers
Answer:
Step-by-step explanation:
$18 would work
And anything below that number.
The price for the caps can be $18.
What is Tax?A tax is a mandatory financial charge or other kind of levy placed on a taxpayer by a government agency to pay for government expenses and other public expenditures.
Given:
Sales tax in his city is 8%.
let the price be x.
x( 1+ 8%) ≤ 20
1.08x ≤ 20
x≤ 18.52
So, x can be 18.52 of less than 18.52.
Learn more about Tax here:
https://brainly.com/question/16423331
#SPJ2
a business magazine was conducting a study into the amount of travel required for mid-level managers across the u.s. eighty-six managers were surveyed for the number of days they spent traveling each year. mid-level manager travel days traveling frequency 0 -6 13 7 -13 25 14 -20 35 21 -27 6 28 -34 4 35 and above 3 step 1 of 2 : determine the cumulative frequency of the third class.
Answers
The cumulative frequency of the third class is 73. This means that 73 out of the 86 mid-level managers surveyed spent between 14 and 20 days traveling each year.
The cumulative frequency of the third class is the sum of the frequencies of all the classes up to and including the third class. In this case, the frequency of the third class is 35, and the frequencies of the first two classes are 13 and 25, respectively. So, the cumulative frequency of the third class is:
13 + 25 + 35 = 73
This means that 73 out of the 86 mid-level managers surveyed spent between 14 and 20 days traveling each year.
Learn more about cumulative :
https://brainly.com/question/15088938
#SPJ4
If f(x) = -2x + 3 and g(x) = 4x - 3, which is greater, f(5) or g(-2)?
Answers
Solve the equation v + f – e = 2 for e.
Answers
Answer:
e = -2 + v + f
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightEquality Properties
Multiplication Property of Equality Division Property of Equality Addition Property of Equality Subtract Property of EqualityStep-by-step explanation:
Step 1: Define
v + f - e = 2
Step 2: Solve for e
Subtract v on both sides: f - e = 2 - vSubtract f on both sides: -e = 2 - v - fDivide -1 on both sides: e = -2 + v + fWhich table represents an exponential function
Answers
Answer:
Step-by-step explanation:
table3 represents exponential function
how many solutions can a quadratic have
a.0 solution
b.1 solution
c.2 solutions
d.3 solutions
Answers
Solve the following 2 equation system for X and Y : Y=2X+1 (i) X=7−2Y (ii) The value of X is equal to:
Answers
Answer: X = -1/2
Step-by-step explanation:
(i) Y = 2X + 1
(ii) X = 7 - 2Y
We can substitute the value of X from equation (ii) into equation (i) and solve for Y.
Substituting X = 7 - 2Y into equation (i), we have:
Y = 2(7 - 2Y) + 1
Simplifying:
Y = 14 - 4Y + 1
Y = -3Y + 15
Adding 3Y to both sides:
4Y = 15
Dividing both sides by 4:
Y = 15/4
Now, we can substitute this value of Y back into equation (ii) to find X:
X = 7 - 2(15/4)
X = 7 - 30/4
X = 7 - 15/2
X = 14/2 - 15/2
X = -1/2
Therefore, the value of X is -1/2 when solving the given system of equations.
The solution to the system of equations Y=2X+1 and X=7−2Y is X=1 and Y=3.
Explanation:To solve this system of equations, you can start by substituting y in the second equation with the value given in equation (i) (2x+1). So, the second equation will now be X = 7 - 2*(2x+1).
This simplifies to X = 7 - 4x - 2. Re-arrange the equation to get X + 4x = 7 - 2, which further simplifies to 5x = 5, and thus x = 1.
Now that you have the value of x, you can substitute that in the first equation to find y. Hence, Y = 2*1 + 1 = 3.
Therefore, the solution to this system of equations is X = 1 and Y = 3.
Learn more about System of Equations here:https://brainly.com/question/35467992
#SPJ2
A triangle has side lengths of 8cm, 10cm and 14cm, classify it as acute, obtuse or right
Answers
A triangle with the sides of lengths 8 cm, 10 cm, and 14 cm is an Obtuse triangle.
We solve question By the Pythagoras theorem
If the three sides of a triangle are a , b and c,
If a² + b² = c² ⇒ a right triangle.
If a² + b² < c² ⇒ an obtuse triangle.
If a² + b² > c² ⇒ an acute triangle.
At question above,triangle sides are 8 cm, 10 cm, and 14 cm.
Apply to Pythagoras theorem:
8² + 10² = 64 + 100 = 164
And, 14² = 196
Therefore, 8² + 10² < 14²
About Obtuse TriangleAn obtuse triangle is a triangle in which one of the angles is greater than 90⁰.
The characteristic of an obtuse triangle is that it looks sharp. Therefore, an obtuse triangular shape looks like a needle.
The condition for an obtuse triangle is that one of its corners must have an angle of more than 90⁰.
The sum of the angles of an obtuse triangle add up to 180⁰.
Characteristics of an Obtuse Triangle
The properties of an obtuse triangle are:
• Has one obtuse angle and two acute angles
• One of the angles is greater than 90⁰
• The sum of the three angles is 180°
• The sum of the two sides is greater than the length of the other side
Learn more about triangle at
https://brainly.com/question/9155927
#SPJ4
The following are the weights (in pounds) of seven people:
100, 115, 135, 140, 180, 197, 230.
find the 80th percentile.
Answers
The 80th percentile is 125.37.
It is required to find the solution.
What is percentage?A part of a whole expressed in hundredths a high percentage of students attended. Also the result obtained by multiplying a number by a percent the percentage equals the rate times the base.
Given:
The weights (in pounds) of seven people:
100, 115, 135, 140, 180, 197, 230.
We have to find the 80th percentile first we have to find the mean of seven people.
Mean=100+ 115+135+140+ 180+197+ 230/7
Mean=156.71
100 percent=156.71
80 percent=156.71*80/100
80 percent=125.37.
Therefore, the 80th percentile is 125.37.
Learn more about percentage here
https://brainly.com/question/28269290
#SPJ4
The elevation of a city is positive if the city is above sea level and negative if below sea level. The elevation of New Orleans is -0.3 \text{ m}−0.3 mminus, 0, point, 3, start text, space, m, end text. What does an elevation of -0.3 \text{ m}−0.3 mminus, 0, point, 3, start text, space, m, end text represent in this situation? Choose 1 answer: Choose 1 answer: (Choice A) A New Orleans is 0.3 \text{ m}0.3 m0, point, 3, start text, space, m, end text above sea level. (Choice B) B New Orleans is at sea level. (Choice C) C New Orleans is 0.3 \text{ m}0.3 m0, point, 3, start text, space, m, end text below sea level.
Answers
Answer:
Yes
Step-by-step explanation:
Answer:
the anwser is below sea level
Step-by-step explanation:
The perimeter of a rectangular meadow is 1004 m. What
will be the sum of the length and breadth of the meadow ?
Answers
Answer:
hope it works for u
Step-by-step explanation:
Given the length of the rectangle = l
the breadth of the rectangle = b
perimeter of the rectangle = sum of length of all sides of the rectangle
= l+ b+ l+ b
=2 l+2 b
=2( l+ b)
∴ perimeter of the rectangle =2( l+ b)
as given perimeter = 1004 m
hence ,
2(l+ b)= 1004
(l+ b)=1004/2 = 502 m
l+ b=502 m