Sample _________ play a very critical role to determine whether or not to ""reject the null hypothesis"" or ""do not reject the null hypothesis"".
Answers
Sample statistics play a very critical role in determining whether to "reject the null hypothesis" or "do not reject the null hypothesis."
In hypothesis testing, the null hypothesis represents the claim or assumption being tested, while the alternative hypothesis proposes a different claim. The goal is to assess the evidence provided by the sample data to make a decision about the null hypothesis.
To make this decision, statistical tests are performed using the sample data. These tests involve calculating sample statistics, such as means, proportions, or test statistics, which are compared to the expected values under the null hypothesis.
By comparing the sample statistics to the expected values, we can assess whether the observed data is consistent with the null hypothesis or suggests evidence against it. If the sample statistics provide strong evidence against the null hypothesis, we may reject it in favor of the alternative hypothesis. On the other hand, if the sample statistics do not provide sufficient evidence, we do not have enough grounds to reject the null hypothesis.
Therefore, sample statistics play a crucial role in determining whether to "reject the null hypothesis" or "do not reject the null hypothesis" based on the evidence provided by the sample data.
Learn more about hypothesis here:
brainly.com/question/32562440
#SPJ11
Related Questions
Consider the function f(x) = x2 - 4x + 8 on the interval 0, 4. Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0. Find all such values c and enter them as a comma-separated list. Values of c =: (1 point) Consider the function graphed below. P n ? Does this function satisfy the hypotheses of the Mean Value Theorem on the interval a, b ? Does it satisfy the conclusion?? f(b) f(a)2 At what point c is f'(c) b - a
Answers
Verifying that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c = 2 such that f'(c) = 0.
Given:
Consider the function f(x) = x2 - 4x + 8 on the interval 0, 4. Verify that this function satisfies the three hypotheses of Rolle's Theorem on the inverval f(x) is f(x) is and f(0) on [0, 4] on (0, 4) f(4) Then by Rolle's theorem, there exists at least one value c such that f'(c) = 0.
f(x)=x^2−4x+8, [0,4]
when, x = 0
f(x) = x^2 -4x +8
f(0) = y = 0 - 0 + 8 = 8
when, x=4
f(5) = y = 16 - 16+8 =
thus, we have 2 points (0, 8) ; (4, 8)
slope,m = {8-(8)} / {4-0} = 0
hence, we have to calculate all the points,x where 0<x<8 and slope=0
f '(x) = 2x - 4 = 0
or, f '(c) = 2c - 4 = 0
c = 4/2 =2 ( 0<x<4)
hence, the there is only one solution c=2 which satisfies Rolle's theorem.
Learn more about the rolle's theorem here:
https://brainly.com/question/13972986
#SPJ4
A cube can be unfolded into the net shown below. Find the total
surface area of the cube.
23.9 mm
Answers
Answer:
23.9 mm
Step-by-step explanation:
A cube can be unfolded into the net shown below. Find the total
surface area of the cube.
23.9 mm
21. Find *problem in pic*
Write in simplest form.
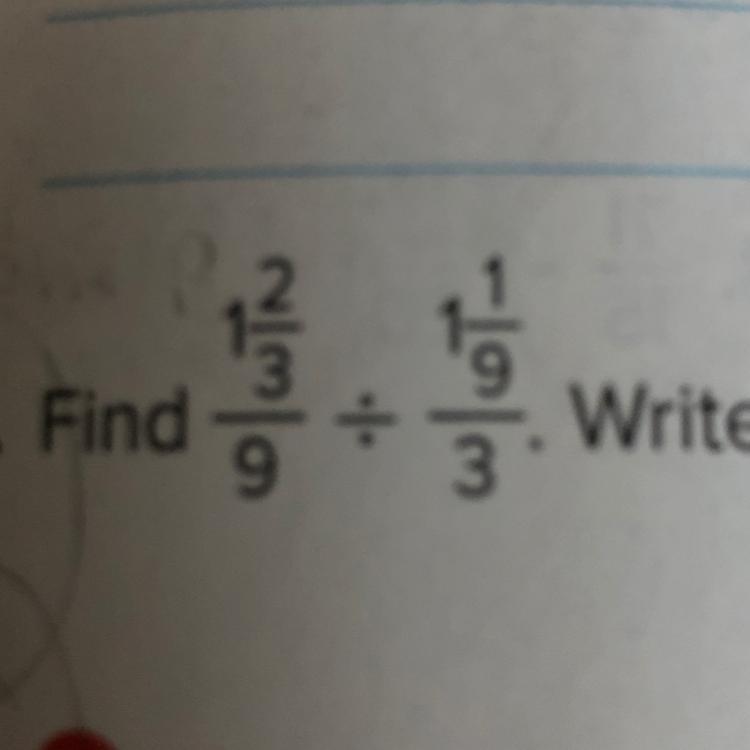
Answers
Answer:
The equation would be wrote (5/25 ÷ 10/25)
TRUE OR FALSE: The alternative hypothesis states that there is no difference/no effect.
Answers
The answer is FALSE. The alternative hypothesis is a statement that there is a difference or an effect in the population being studied, and it contradicts the null hypothesis, which is a statement that there is no difference or no effect in the population being studied.
The alternative hypothesis is a statement that contradicts the null hypothesis and is generally the hypothesis that the researcher wants to support. It is a statement that there is a difference or an effect in the population being studied.
In hypothesis testing, the null hypothesis is a statement that there is no difference or no effect in the population being studied. The null hypothesis is typically the default hypothesis, which is assumed to be true unless evidence suggests otherwise. The alternative hypothesis, on the other hand, is a statement that there is a difference or an effect in the population being studied, and it is typically the hypothesis that the researcher wants to support.
For example, if a researcher wants to test the effectiveness of a new drug, the null hypothesis might be that the drug has no effect on the condition being treated, while the alternative hypothesis might be that the drug has a positive effect on the condition being treated.
In summary, the alternative hypothesis is a statement that there is a difference or an effect in the population being studied, and it contradicts the null hypothesis, which is a statement that there is no difference or no effect in the population being studied.
To know more about hypothesis:
https://brainly.com/question/14957391
#SPJ11
12
Calculate the area of the given segment. Round your answer to the nearest tenth, if necessary.
60
8 in.

Answers
Check the picture below.
\(\textit{area of a segment of a circle}\\\\ A=\cfrac{r^2}{2}\left( ~~ \cfrac{\pi \theta }{180}-\sin(\theta ) ~~ \right) \begin{cases} r=radius\\ \theta =\stackrel{degrees}{angle}\\[-0.5em] \hrulefill\\ r=8\\ \theta =60 \end{cases} \\\\\\ A=\cfrac{8^2}{2}\left( ~~ \cfrac{\pi (60) }{180}-\sin(60^o ) ~~ \right)\implies A=32\left( ~~ \cfrac{\pi }{3}-\sin(60^o ) ~~ \right) \\\\\\ A=32\left( ~~ \cfrac{\pi }{3}-\cfrac{\sqrt{3}}{2} ~~ \right)\implies A=\cfrac{32\pi }{3}-16\sqrt{3}\implies A\approx 5.8~in^2\)

What is the greatest common factor (GCF) of 51 and 68?
A. 12
B. 3
C. 17
D. 2
Answers
Factors of 51: 1, 3, 17, 51
Factors of 68: 1, 2, 4, 17, 34, 68
As you can see the greatest common factor of both numbers is 17.
Therefore, the answer is C.
Best of Luck!
students from a class of 15 are going to be chosen to be on the dance committee. Find the number of different 4-person committees that can be made.
Answers
we know that
The formula for combinations is
\(C=n!/[(n-r)!*r!]\)
where
\(n\) is the total number of objects you choose from
\(r\) is the number that you choose to arrange
in this problem
\(n=15\) students
\(r=4\) students
\(C=15!/[(15-4)!*4!]\) → \(C=15!/[11!*4!]\) → \((15*14*13*12*11!)/(11!*4*3*2*1)\)
\(C=(15*14*13*12)/(24)\) → \(C=1365\)
the answer is
1,365
To solve the equation 2−5(3+4x)=2x+7, Miranda's first step was to write 2−15−20x=2x+7. Which property did Miranda use in her first step?
Answers
Answer:
Step-by-step explanation:
distributive
In the expansion of (2a + 4b)8, which of the following are possible variable terms? Explain your reasoning.
a2b3; a8; a5b3; ab8; a3b5; a7b; a6b5; b8

Answers
In the expansion of (2a+4b)⁸ the possible variable terms are a⁸, a⁵b³, a³b⁵, a⁷b, and b⁸.
What is an Expression?In mathematics, an expression is defined as a set of numbers, variables, and mathematical operations formed according to rules dependent on the context.
The expansion is given by the following formula: \(\left(a + b\right)^{n} = \sum_{k=0}^{n} {\binom{n}{k}} a^{n - k} b^{k}\), where \({\binom{n}{k}} = \frac{n!}{\left(n - k\right)! k!}\)
As given to us, a = 2a, b = 4 b, and n = 8.
Therefore, \(\left(2 a + 4 b\right)^{8} = \sum_{k=0}^{8} {\binom{8}{k}} \left(2 a\right)^{8 - k} \left(4 b\right)^{k}(2a+4b)\).
Thus, \(\left(2 a + 4 b\right)^{8} = 256 a^{8} + 4096 a^{7} b + 28672 a^{6} b^{2} + 114688 a^{5} b^{3} + 286720 a^{4} b^{4} + 458752 a^{3} b^{5} + 458752 a^{2} b^{6} + 262144 a b^{7} + 65536 b^{8}.\)
Hence, In the expansion of (2a+4b)⁸ the possible variable terms are a⁸, a⁵b³, a³b⁵, a⁷b, and b⁸.
Learn more about Expression:
https://brainly.com/question/13947055
#SPJ1
It is easy
(just not for me)

Answers
Do you want me to solveee orrrrrrrrrrrr???
A round fountain has a radius of 86cm. What is the circumstance of the fountain, in meters?
Answers
Answer:
The circumference of any circle is 2πr, where r is the radius.
Step-by-step explanation:
If x = 3 , solve for y.
y = 2 * 3 ^ 3
Next, solve the equation using order of operations.
Exponents first.
y =2*[?]
Answers
Answer:
If $x=3$, then $y=2*3^{3}$. Using order of operations, we evaluate the exponent first, then perform the multiplication:
\begin{align*}
y &= 2 * 3^{3} \\
&= 2 * 27 \\
&= 54
\end{align*}
Therefore, $y=54$.
PLs help with this one yallllll

Answers
Answer:
yes, because 6 is less than 11
Step-by-step explanation:
Hope this helps!!
Mark me brianliest and good luck!!
negative one-third divided by five-fourths divided by negative two-fifths equals?
Answers
The solution of the division of the fraction is expressed as; -⁴/₁₅
How to divide fractions?When dividing fractions, what will carry out first is to turn it into multiplication. Thereafter, we will make use of the multiplicative inverse (reciprocal) to multiply.
We have the expression as;
-¹/₃ ÷ ⁵/₄
By the method described above, we can say that the solution is;
-¹/₃ × ⁴/₅
= -⁴/₁₅
Read more about Fraction division at; https://brainly.com/question/4917910
#SPJ1
What is the slope of the line?

Answers
Answer:
1 or x (the equation is y=x+1)
Step-by-step explanation:
the perimeter of the triangle below is 38 units. Find the length of side WX. Write your answer without variables

Answers
Answer:
5.5
Step-by-step explanation:
Add each side of the triangle.
3z+z+1+4z-3 = 8z - 2
8z - 2 is equivalent to the perimeter.
Since you know the perimeter is 38 units, you can set 8z-2 to 38.
8z-2 = 38
Solve for z. Subtract 2 from each side.
8z = 36
Divide each side by 8.
z = 4.5
Now solve for side WX.
WX = z + 1
WX = 4.5 + 1
WX = 5.5
What is the approximate radius of a sphere with a surface area of 65π inches
Answers
\(\textit{volume of a sphere}\\\\ V=\cfrac{4\pi r^3}{3}~~ \begin{cases} r=radius\\[-0.5em] \hrulefill\\ V=65\pi \end{cases}\implies 65\pi =\cfrac{4\pi r^3}{3}\implies \cfrac{3}{4\pi}\cdot 65\pi =r^3 \\\\\\ \cfrac{195}{4}=r^3\implies \sqrt[3]{\cfrac{195}{4}}=r\implies 3.65\approx r\)
THERE IS 5 QUESTIONS I NEED TO GET DONE IN TOTAL, BUT IT WONT LET ME PUT MANY PICS IN ONE QUESTION SO PLS GO TO MY ACC AND VIEW THE OTHER 2!!I NEED THIS BY **TODAY**

Answers
Answer:
given in picture
Step-by-step explanation:
(-2,10) (-1,7) (0,4) (1,1) (2,-2) (3,-5)

Linea 6: cada 45 minutos linea 15: cada 15 minutos linea 10: cada 30 minutos rapidos por autopista: cada 90 minutos ¿coinciden en algun momentos todas las lineas, menos el rapido? Explica tu respuesta
Answers
Answer:
Las tres líneas coinciden cada 90 minutos, es decir, al mismo tiempo que pasa el Rápido, con lo cual en ningún momento coinciden todas las líneas menos el Rápido.
Step-by-step explanation:
Dado que la Línea 6 pasa cada 45 minutos, la Línea 15 pasa cada 15 minutos, la Línea 10 pasa cada 30 minutos, y los Rápidos por autopista pasan cada 90 minutos, para determinar si coinciden en algún momento todas las líneas, menos el rápido, se deben realizar los siguientes cálculos:
Línea 6 = 00:45, 01:30, 02:15, 03:00
Línea 15 = 00:15, 00:30, 00:45, 01:00, 01:15, 01:30, 01:45, 02:00, 02:15, 02.30, 02:45, 03:00
Línea 10 = 00:30, 01:00, 01:30, 02:00, 02:30, 03:00
Rápido = 01:30, 03:00
Así, como puede verse, las tres líneas coinciden cada 90 minutos, es decir, al mismo tiempo que pasa el Rápido, con lo cual en ningún momento coinciden todas las líneas menos el Rápido.
A=3.14r^2, If A=49, find r?
Answers
Answer:
Step-by-step explanation:
Isolate the variable by dividing each side by factors that don't contain the variable.
Exact Form:
r=√15.60509554,√15.60509554
r=15.60509554,15.60509554
Decimal Form:
r=3.95032853…,3.95032853…
How is the number 6.237 read?
A. Six and two hundred thirty-seven thousandths
B. Sixty-two and thirty-seven thousandths
C. Sixty-two and thirty-seven tenths
D. Six and two hundred thirty-seven tenths
Answers
Answer:
I believe it's either between a or d
Step-by-step explanation:
I am not really sure but hope it helps
Hope you also have a great day!
what steps do you take to check if your multiplication is right?
Answers
Here is step-by-step answer.
Step 1b: Fill in your times tables answers in sequence and check if you got them all right. Step 2: Drag the correct answers to the questions. Step 3: Fill in your answers for the mixed questions and check if you got them all right. Step 4: Multiple choice questions will help you to improve by looking at the questions in a different way.
Consider two linear transformations:Rα :R2 →R2 and Rβ :R2 →R2given by rotation counter-clockwise around the origin by α and β, respectively.(a) Describe the composition Rα ◦ Rβ geometrically. What is it doing to the space R2? (b) Find the standard matrix of the composition Rα ◦ Rβ , using your answer to (a).(c) Find the standard matrix of the composition Rα ◦ Rβ a different way.(d) Use your answers to (b) and (c) to derive formulas for sin(α + β) and cos(α + β).
Answers
a) The composition Rα ◦ Rβ rotates the space R2 by an angle of (α + β) counter-clockwise around the origin.
b) The standard matrix of Rα ◦ Rβ is \begin{bmatrix} cos(α + β) & -sin(α + β) \ sin(α + β) & cos(α + β) \end{bmatrix}.
c) The standard matrix of Rα ◦ Rβ is calculated by multiplying the standard matrices of Rα and Rβ.
d) The formulas for sin(α + β) and cos(α + β) in terms of sin(α), sin(β), cos(α), and cos(β) are: sin(α + β) = sin(α)cos(β) + cos(α)sin(β) and cos(α + β) = cos(α)cos(β) - sin(α)sin(β).
a) Geometrically, the composition Rα ◦ Rβ is the rotation of R2 counter-clockwise around the origin by an angle of (α + β). This is because Rα rotates R2 counter-clockwise around the origin by an angle of α, and Rβ rotates R2 counter-clockwise around the origin by an angle of β. This composition is therefore rotating the space R2 by an angle of (α + β).
b) The standard matrix of the composition Rα ◦ Rβ is:
\begin{bmatrix}
cos(α + β) & -sin(α + β) \\
sin(α + β) & cos(α + β)
\end{bmatrix}
c) We can also use the properties of matrix multiplication to find the standard matrix of the composition Rα ◦ Rβ. We know that the standard matrices for Rα and Rβ are:
Rα = \begin{bmatrix}
cos(α) & -sin(α) \\
sin(α) & cos(α)
\end{bmatrix}
Rβ = \begin{bmatrix}
cos(β) & -sin(β) \\
sin(β) & cos(β)
\end{bmatrix}
Therefore, the standard matrix of the composition Rα ◦ Rβ is:
Rα ◦ Rβ = \begin{bmatrix}
cos(α)cos(β) - sin(α)sin(β) & -sin(α)cos(β) - cos(α)sin(β) \\
cos(α)sin(β) + sin(α)cos(β) & sin(α)sin(β) + cos(α)cos(β)
\end{bmatrix}
d) By comparing our two standard matrices for Rα ◦ Rβ, we can see that:
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
cos(α + β) = cos(α)cos(β) - sin(α)sin(β)
Therefore, the composition of Rα and Rβ rotates the space R2 by an angle of (α + β) counter-clockwise around the origin, and its standard matrix is calculated by multiplying the standard matrices of Rα and Rβ.
To know more about standard matrix click here:
https://brainly.com/question/31040879
#SPJ11
There are 10 rows of flowers in the garden. Each row has 6 roses, 4 mums, and 5 tulips. Which expression represents this situation
Answers
Answer:
10(6 + 4 + 5)
Step-by-step explanation:
What is probability? Can you give an example?
What is the difference between certain and impossible events?
What is the difference between theoretical and experimental probability? Can you give an example?
Given an experiment, can you answer questions about the probability?
Answers
Answer:
Step-by-step explanation:
We can calculate probability by looking at the outcomes of an experiment or by reasoning about the possible outcomes.
Write the first five digits of 1/7 in base 9 expression
Answers
Compare 1/7 to consecutive multiples of 1/9. This is easily done by converting the fractions to a common denominator of LCM(7, 9) = 63:
1/9 = 7/63
2/9 = 14/63
while
1/7 = 9/63
Then 1/7 falls between 1/9 and 2/9, so 1/7 = 1/9 plus some remainder. In particular,
1/7 = 1/9¹ + 2/63.
We do the same sort of comparison with the remainder 2/63 and multiples of 1/9² = 1/81. We have LCM(63, 9²) = 567, and
1/9² = 7/567
2/9² = 14/567
3/9² = 21/567
while
2/63 = 18/567
Then
2/63 = 2/9² + 4/567
so
1/7 = 1/9¹ + 2/9² + 4/567
Compare 4/567 with multiples of 1/9³ = 1/729. LCM(567, 9³) = 5103, and
1/9³ = 7/5103
2/9³ = 14/5103
3/9³ = 21/5103
4/9³ = 28/5103
5/9³ = 35/5103
6/9³ = 42/5103
while
4/567 = 36/5103
so that
4/567 = 5/9³ + 1/5103
and so
1/7 = 1/9¹ + 2/9² + 5/9³ + 1/5103
Next, LCM(5103, 9⁴) = 45927, and
1/9⁴ = 7/45927
2/9⁴ = 14/45927
while
1/5103 = 9/45927
Then
1/5103 = 1/9⁴ + 2/45927
so
1/7 = 1/9¹ + 2/9² + 5/9³ + 1/9⁴ + 2/45927
One last time: LCM(45927, 9⁵) = 413343, and
1/9⁵ = 7/413343
2/9⁵ = 14/413343
3/9⁵ = 21/413343
while
2/45927 = 18/413343
Then
2/45927 = 2/9⁵ + remainder
so
1/7 = 1/9¹ + 2/9² + 5/9³ + 1/9⁴ + 2/9⁵ + remainder
Then the base 9 expansion of 1/7 is
0.12512..._9
Find the CI, if Rs 5000 was invested for 2 years at 10% p.a. compounded half-yearly?
Best answers needed
Quickly! pls!
Don't Spam
Answers
Answer:
Given:
A sum of Rs 5000 was invested for 2 years at 10% p.a. compounded half - yearly.To Find:
The compound Interest.Solution:
★ Firstly, we have to find the amount:
According, to the question by using the formula, we get:
\( \longmapsto \: { \bold{ \boxed{\pink{ \rm{A \: = P \left( 1 + \frac{ \frac{r}{2} }{100} \right)^{2n} }}}}}\)
Here,
Amount (A) = A Principal (P) = Rs 5000 Rate of Interest (r) = 10% p.a Time Period (n) = 2 yearsSo by putting their values, we get:
\( { \large{\longrightarrow{ \rm{A = 5000 \left( 1 + \frac{ \frac{10}{2} }{100} \right)^{2 \times 2} }}}}\)
\( { \large{ \longrightarrow{ \rm{A = 5000 \left( 1 + \frac{10}{2} \times \frac{1}{100} \right)^{4} }}}}\)
\( {\large{ \longrightarrow{ \rm{A = 5000 \left( 1 + \frac{10 \times 1}{2 \times 100} \right)^{4} }}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \left(1 + \frac{10}{200} \right)^{4} }}}}\)
\({ \large \longrightarrow {\rm{A =5000 \left( \frac{200 \times 1 + 10}{200} \right)^{4} }}}\)
\({ \large \longrightarrow{ \rm{A = 5000 \left( \frac{200 + 10}{200} \right)^{4} }}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \left( \frac{210}{200} \right)^{4} }}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \left( \frac{210}{200} \times \frac{210}{200} \times \frac{210}{200} \times \frac{210}{200} \right)}}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \left( \frac{210 \times 210 \times 210 \times 210}{200 \times 200 \times 200 \times 200} \right)}}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \left( \frac{1944810000}{1600000000} \right)}}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \times \frac{1944810000}{1600000000} }}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5000 \times \frac{194481}{160000} }}}}\)
\({ \large{ \longrightarrow{ \rm{A = 5 \times \frac{194481}{160} }}}}\)
\({ \large{ \longrightarrow{ \rm{A = \frac{972405}{160} }}}}\)
\({ \large{ \longrightarrow{ \rm{A = 6077.53 \: (approx.)}}}}\)
Hence, the amount is Rs 6078.
★ Now, we have to find the compound Interest:
According, to the question by using the formula, we get:
\({ \large{ \dashrightarrow{ \boxed{\green{ \rm{Compound \: Interest = A \: - \: P}}}}}}\)
Here,
Amount (A) = Rs 6078 Principal (P) = Rs 5000So, by putting their values we get:-
\( { \large{ \dashrightarrow{ \rm{Compound \: Interest = Rs \: 6078 \: - \: Rs \: 5000}}}}\)
\({ \large{ \dashrightarrow{ \rm{Compound \: Interest = Rs \: 1078}}}}\)
Hence, Compound Interest is Rs 1078.
A restaurant chef wants to install a new floor in her kitchen. The kitchen measures 8 meters wide and 12 meters long, and the flooring costs $8.00 per square meter. How much will the chef's new floor cost?
Answers
Answer:
$768
Step-by-step explanation:
8 x 12 = 96 m²
1 m² = $8.00
96m² x $8.00 = $768
find the slope of the tangent line at t = -1. b) find the points where the tangent is vertical or horizontal.
Answers
To find the slope of the tangent line at t = -1, we need to take the derivative of the function with respect to t and evaluate it at t = -1. We have the derivative, we substitute t = -1 to find the slope of the tangent line at that point.
The points where the tangent line is vertical or horizontal occur when the derivative is either undefined or equal to zero.
To find the slope of the tangent line at t = -1, we differentiate the given function with respect to t. Let's assume the function is denoted by y(t). We calculate dy/dt, which represents the derivative of y with respect to t. Once we have the derivative, we substitute t = -1 to find the slope of the tangent line at that point.
To find the points where the tangent line is vertical or horizontal, we set the derivative equal to zero and solve for t. This will give us the values of t where the tangent line is horizontal. To find the points where the tangent line is vertical, we look for values of t where the derivative is undefined. These points correspond to vertical tangents on the graph of the function.
Learn more about function here: brainly.com/question/30721594
#SPJ11
What is the formula for the sum of integers?.
Answers
The sum of integers is: S = n(a + l)/2
Integer numbers are those without fractional or decimal parts. When there are fewer numbers to add, it is possible to determine the sum of integers using basic mathematics. However, we employ the sum of integers formula if we need to add multiple consecutive integers at once. Our computations are made easier, and the amount of time we spend adding is reduced.
The sum of an arithmetic sequence's n terms is what is meant by the sum of integers formula. The formula for the sum of integers is:
S = n(a + l)/2
where,
S = sum of the consecutive integers
n= number of integers
a= first term
l = last term
Know more about Integer at:
https://brainly.com/question/26009132
#SPJ4