s = vt + 16t2 for v.
Answers
Answer:
s = vt + 16t^2
s -16t^2 = vt
s/t -16t = v
Answer:
v = s/t -16t
Step-by-step explanation:
Related Questions
The nearest whole number.
12) Huong enlarged the size of a painting to a
width of 12 cm. What is the new height if
it was originally 4 cm wide and 3 cm tall?
Answers
The nearest whole number to which the new height of the image is enlarged is 9cm.
What is scaling?By scaling, we can create a drawing of an object that corresponds to the object's true size. In geometry, scaling refers to either growing or reducing figures in order to preserve their fundamental shape. Similar figures are what we call scaled figures.
Given that the original size was in the ratio 4: 3.
When the image is enlarged the enlarged image will be in the similar ratio to the original size.
Hence, the ratio in which the enlarged image will be increased is 4x : 3x.
The new width is given as 12,
The value of 4x = 12
x = 3
Then the new height of the image is:
3 (3) = 9cm.
Hence, the new height of the image is 9cm.
Learn more about ratio here:
https://brainly.com/question/13419413
#SPJ1
In science class, Mrs. Moore's students were directed to weigh a 300-gram mass on the balance scale. Tina weighed
the object and reported 328 grams.
Answers
Answer: 9 1/3%
Step-by-step explanation:
1.1-6. If P(A)=0.5,P(B)=0.6, and P(A∩B)=0.4, find (a) P(A∪B), (b) P(A∩B′), and (c) P(A′∪B′). 1.1-7. Given that P(A∪B)=0.76 and P(A∪B′)=0.87, find P(A).
Answers
(a) To find P(A∪B), we can use the formula P(A∪B) = P(A) + P(B) - P(A∩B). Substituting the given values, P(A∪B) = 0.5 + 0.6 - 0.4 = 0.7.
(b) To find P(A∩B′), we can use the formula P(A∩B′) = P(A) - P(A∩B). Substituting the given values, P(A∩B′) = 0.5 - 0.4 = 0.1.
(c) To find P(A′∪B′), we can use the formula P(A′∪B′) = 1 - P(A∪B). Substituting the given values, P(A′∪B′) = 1 - 0.7 = 0.3.
(a) P(A∪B) represents the probability of either event A or event B occurring. To calculate it, we use the inclusion-exclusion principle. We add the individual probabilities of A and B and then subtract the probability of their intersection. So, P(A∪B) = P(A) + P(B) - P(A∩B) = 0.5 + 0.6 - 0.4 = 0.7.
(b) P(A∩B′) represents the probability of event A occurring but not event B. We can find it by subtracting the probability of A and B occurring together (P(A∩B)) from the probability of A occurring (P(A)). Therefore, P(A∩B′) = P(A) - P(A∩B) = 0.5 - 0.4 = 0.1.
(c) P(A′∪B′) represents the probability of neither A nor B occurring. We can find it by subtracting the probability of A∪B (both A and B occurring) from 1. Therefore, P(A′∪B′) = 1 - P(A∪B) = 1 - 0.7 = 0.3.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Deside weather each equation is true for all one or no values of x? 9(x-2)= 7x+5
Answers
Equation is true for one x and that x = 23/2
What is the solution to an equation?
In order to make the equation's equality true, the unknown variables must be given values as a solution. In other words, the definition of a solution is a value or set of values (one for each unknown) that, when used as a replacement for the unknowns, transforms the equation into equality.
Find x.
9(x - 2) = 7x + 5
Distribute x
9x - 18 = 7x + 5
9x - 7x = 5 + 18
2x = 23
x = 23/2
Equation is true for one x and that x = 23/2
To learn more about the solution of an equation from the given link
https://brainly.com/question/22688504
#SPJ1
Tommy walks at a rate of `2` feet per minute.
Right now, he is at `-60` feet.
Where were Tommy `10` minutes
Answers
Hope this helps you
List the quadrant or quadrants satisfying the following condition. xy>0 Select all that apply. A. quadrant IV B. quadrant III C. quadrant II D. quadrant I.
Answers
The quadrants that satisfy the condition xy>0 are quadrant I and quadrant III.
The product of two numbers is positive if and only if both numbers have the same sign. In other words, if x and y are both positive or both negative, then xy will be positive.
Quadrant I and quadrant III are the only quadrants where both x and y are positive. Quadrant II and quadrant IV are the only quadrants where both x and y are negative.
Therefore, the only quadrants that satisfy the condition xy>0 are quadrant I and quadrant III.
Here is a table that shows the signs of x and y in each quadrant:
Quadrant | x | y | xy
------- | --- | --- | ---
I | + | + | +
II | + | - | -
III | - | - | +
IV | - | + | -
Learn more about quadrant here:
brainly.com/question/30979352
#SPJ11
The quadrants that satisfy the condition xy>0 are quadrant I and quadrant III.
The product of two numbers is positive if and only if both numbers have the same sign. In other words, if x and y are both positive or both negative, then xy will be positive.
Quadrant I and quadrant III are the only quadrants where both x and y are positive. Quadrant II and quadrant IV are the only quadrants where both x and y are negative.
Therefore, the only quadrants that satisfy the condition xy>0 are quadrant I and quadrant III.
Here is a table that shows the signs of x and y in each quadrant:
Quadrant | x | y | xy
------- | --- | --- | ---
I | + | + | +
II | + | - | -
III | - | - | +
IV | - | + | -
Learn more about quadrant here: brainly.com/question/30979352
#SPJ11
Find the zeros of the function enter the solutions from least to greatest\(H(x)=-5x^2+180\)
Answers
Answer:
x=36
Step-by-step explanation:
The ratio of credit card sales to cash sales at a store was 8:3. If the store had 144 cash sales, how many more credit card sales were there than cash sales?
Answers
Answer:
There were 240 more credit card sales than cash sales.
Step-by-step explanation:
By using the ratio 8:3 I was able to determine that if there were 144 cash sales that would mean that there would be 384 credit card sales. However, the question asks "How many more credit card sales were there than cash sales?" Meaning that we need to find the difference. 384-144= 240.
This means that there were 240 more credit card sales than cash sales.
Hope this helped! If you have any questions about what I did please comment!
And if this helped please mark brainliest!
Have a great day!!
Find the distance between the points (6,2) and (2,5),
1. Formula set up correctly.
2. All steps shown.
3. Correct answer
Answers
The distance between the points (6,2) and (2,5) is 5 units.
To find the distance between the points (6,2) and (2,5), follow these steps:
1. Formula set up correctly: Use the distance formula, which is d = √((x2 - x1)² + (y2 - y1)²), where (x1, y1) and (x2, y2) are the coordinates of the two points.
2. All steps shown:
a. Identify the coordinates: (x1, y1) = (6, 2) and (x2, y2) = (2, 5).
b. Substitute the coordinates into the formula: d = √((2 - 6)² + (5 - 2)²).
c. Simplify the expression inside the parentheses: d = √((-4)² + (3)²).
d. Square the numbers inside the parentheses: d = √(16 + 9).
e. Add the numbers inside the square root: d = √(25).
3. Correct answer: The distance between the points (6,2) and (2,5) is √(25), which simplifies to 5 units.
Learn more about distance here,
https://brainly.com/question/17273444
#SPJ11
Pls solve with steps

Answers
B. 5=2x so 5/2 =x.
C. 2x+1=3 subtract the 1 over which will equal 2x=2 so x=1
D. On this one you have to have the same first number and it would be easier to make it 2^3(70) which is 210=x.
find the value of x and y pls help

Answers
Answer:
x = 50° and y = 80°
Step-by-step explanation:
x + 130° = 180° { being linear pair }
x = 180° - 130°
x = 50°
And we can see in the triangle two sides are equal so it is an isosceles triangle so the base angles are also equal.
Then
y + 50° + 50° = 180° { being sum of angles of triangle }
y + 100° = 180°
y = 180° - 100°
y = 80°
Hope it will help :)❤
Is the sequence arithmetic, geometric or neither? Then, find the next three terms. 0, 3, 6, 9, 12, ___, ___, ____.
alsoo im like rly booorrreddddddd any one wanna talk??
female 14
Answers
Is 3, 6, 9, 12 ,15, 18, 21
it's an arithmetic sequence with initial term 3 and common difference 3.
The graph of a quadratic function with vertex (1,-1) is shown in the figure below. Find the domain and the range. Write your answers as inequalities, using or as appropriate. Or, you may instead click on "Empty set" or "All reals" as the answer.
Answers
The domain of the function is all real numbers and range is y ≥ -1.
Since the vertex is at (1,-1), the axis of symmetry is x = 1.
This means that the domain of the function is all real numbers.
To find the range, we need to consider the y-values of the graph. Since the vertex is the lowest point of the graph, the range must be all y-values greater than or equal to -1.
However, since the parabola opens upwards, there is no upper bound on the y-values.
Therefore, the range is given by y ≥ -1.
Hence, the domain of the function is all real numbers and range is y ≥ -1.
To learn more on Functions click:
https://brainly.com/question/30721594
#SPJ1
if z is a standard normal random variable, what is the probability that z is between -2.4 and 0.4?
Answers
The probability that a standard normal random variable z is between -2.4 and 0.4 is approximately 0.6472.
To find the probability that a standard normal random variable z is between -2.4 and 0.4, we can follow these steps:
Step 1: Look up the cumulative probability corresponding to -2.4 in the standard normal distribution table. The cumulative probability at -2.4 is approximately 0.0082.
Step 2: Look up the cumulative probability corresponding to 0.4 in the standard normal distribution table. The cumulative probability at 0.4 is approximately 0.6554.
Step 3: Subtract the cumulative probability at -2.4 from the cumulative probability at 0.4 to find the probability between the two values:
P(-2.4 < z < 0.4) = 0.6554 - 0.0082
= 0.6472.
Therefore, The probability that z is between -2.4 and 0.4, when z is a standard normal random variable, is approximately 0.6472. This means that there is a 64.72% chance that a randomly selected value from a standard normal distribution falls within the range of -2.4 to 0.4.
To know more about probability, visit:
https://brainly.com/question/32782543
#SPJ11
-2x + y = 0
x - y = -3
Answers
Answer:
The value of x is 3 and y is 6.
Step-by-step explanation:
You can solve this simultaneous equation by elimination method :
\( - 2x + y = 0 - - - (1)\)
\(x - y = - 3 - - - (2)\)
\((1) + (2)\)
\( - 2x + y + x + (- y) = 0 + ( - 3)\)
\( - x = - 3\)
\(x = 3\)
\(substitute \: x = 3 \: into \: (2)\)
\((2)⇒\)
\(3 - y = - 3\)
\( - y = - 6\)
\(y = 6\)
a. The motor vehicle department in a particular state has license plates which contain six characters. Each of the first two characters can be any digit (0-9). Each of the next two characters can be any letter (A-Z). Each of the last two characters can be any letter (A-Z) or digit (0-9). How many different license plates can be printed?
Enter your answer as a whole number.
license plates
b. An automotive dealership offers a particular model of vehicle in 6 different exterior colors, 3 different interior colors and with 4 different option packages. In how many configurations can this vehicle be ordered?
Enter your answer as a whole number.
configurations
c. Jeffrey has jackets in 2 different colors, shirts in 3 different colors, trousers in 4 different colors and ties in 8 different colors/patterns. How many different outfits can Jeffrey make (assuming he doesn't care how well the clothing items will coordinate with each other)?
Enter your answer as a whole number.
Answers
a. There are a total of 676,000 different license plates that can be printed.
b.The vehicle can be ordered in 288 configurations.
c.Jeffrey can make 192 different outfits.
a. To find the number of different license plates that can be printed, we need to calculate the possibilities for each character position.
For the first two characters, each can be any digit from 0 to 9. So, there are 10 possibilities for each position.
For the next two characters, each can be any letter from A to Z. There are 26 letters in the English alphabet, so there are 26 possibilities for each position.
For the last two characters, each can be any letter from A to Z or any digit from 0 to 9. Since there are 26 letters and 10 digits, there are a total of 36 possibilities for each position.
To calculate the total number of different license plates, we multiply the number of possibilities for each position: 10 (for the first digit) * 10 (for the second digit) * 26 (for the third letter) * 26 (for the fourth letter) * 36 (for the fifth character) * 36 (for the sixth character) = 676,000.
b. To determine the number of configurations, we need to multiply the number of choices for each attribute.
For the exterior color, there are 6 options available.
For the interior color, there are 3 options available.
For the option packages, there are 4 options available.
By multiplying these choices together, we get:
6 (exterior colors) * 3 (interior colors) * 4 (option packages) = 72 configurations.
However, each of these configurations can also be ordered with or without an option package, so we need to double the number of configurations.
Therefore, the total number of configurations is:
72 configurations * 2 (with or without option package) = 144 configurations.
c. To calculate the total number of different outfits Jeffrey can make, we need to multiply the number of options for each item of clothing.
Jeffrey has 2 options for jackets, 3 options for shirts, 4 options for trousers, and 8 options for ties. To find the total number of outfits, we multiply these numbers together:
2 (jackets) * 3 (shirts) * 4 (trousers) * 8 (ties) = 192
This means that Jeffrey can make 192 different outfits by choosing any combination of colors/patterns for his jackets, shirts, trousers, and ties.
The multiplication principle, also known as the counting principle, is used to find the total number of outcomes when multiple choices are made independently. In this case, we are assuming that Jeffrey doesn't care about coordinating the different clothing items, so each item can be chosen freely from its available options.
It's important to note that this calculation assumes that Jeffrey will wear only one jacket, one shirt, one pair of trousers, and one tie at a time. If he were to wear multiple items of the same clothing type simultaneously, the number of outfits would be different.
Learn more about Number of different license plates
brainly.com/question/31889594
#SPJ11
PLEASE HELP! Please answer properly. Also don't just multiply the numbers together. I'm supposed to show how I factored it then solved it. Please explain. Can be short explanation.

Answers
Answer:
999975
Step-by-step explanation:
that`s what i got
pls need help very urgent pls fast no fake answer full explanation pls pls

Answers
prime factors of 900 =2 to power 2 ×3 to power 2 × 5 to power 2
: 2 x 375 = 750.
Answer:
6.75 x 10^5
Step-by-step explanation:
Forty percent of a number is greater than one-half the number decreased by 15. Which inequality can be used to determine the number?A 40x > x /2 - 15B 40x > 2x - 15C 0.40x > x/2 - 15D 0.4x < x/2 - 15
Answers
The inequality can be used to determine the number is 0.4x > x/2 - 15
The term inequality means the unequal relationship between the two or more expressions.
Here we have given that Forty percent of a number is greater than one-half the number decreased by 15.
And we need to find the number that is used to determine the inequality.
While we looking into the given question, let us consider x be that unknown number.
Then based on the given statement, we have divide it into two parts.
First, forty percent of the number and it can be written as 40%x or 0.4x.
Next is one-half the number is 1/2 x or x/2
When we combine the whole statement,
Then we get the inequality,
=> 0.4x > x/2 - 15
Therefore option (c) is correct.
To know more about inequality here.
https://brainly.com/question/28823603
#SPJ4
Assume that the Federal Reserve increases the money supply This will cause i. Interest rates to decrease ii. Consumption and investment to decrease iii. Inflation to fall 1. l and ll only 2. II and III only 3. I. II. and III 4. I only
Answers
The correct answer is 1. I and II only. Interest rates to decrease. when the Federal Reserve increases the money supply, it can lead to a decrease in interest rates and an increase in consumption and investment.
When the Federal Reserve increases the money supply, it injects more money into the economy. This can lead to a decrease in interest rates, as there is more money available for borrowing and lending. This is because an increase in the money supply can lead to a decrease in the demand for money, which in turn causes the interest rates to fall.
A decrease in interest rates can lead to an increase in consumption and investment. Lower interest rates make it cheaper for consumers to borrow money to buy goods and services, and for businesses to borrow money to invest in new projects. As a result, an increase in the money supply can lead to an increase in consumption and investment, as businesses and consumers have more money available to spend.
However, an increase in the money supply can also lead to inflation. This is because more money is chasing the same amount of goods and services, leading to an increase in prices. Inflation can erode the purchasing power of money and lead to a decrease in the standard of living.
In conclusion, when the Federal Reserve increases the money supply, it can lead to a decrease in interest rates and an increase in consumption and investment. However, it can also lead to inflation, which can have negative effects on the economy. Therefore, the correct answer is 1. I and II only.
Learn more about Interest rates here
https://brainly.com/question/29802908
#SPJ11
WILL GIVE BRAINLIEST DONT LOOK AT OTHER ANSWERS THEY ARRE WRONG

Answers
Answer:
The first choice, second choice, fifth choice are correct
Step-by-step explanation:
To get the first and second choices, you just need to count the number of boxes. For the fifth choice, you can see that the side lengths have been cut in half from the pre-image to image
Write the equation of a circle where the endpoints of a diameter are (4,9) and (4,-3).
Answers
The equation of a circle having endpoints of diameter as (4,9) and (4,-3) is (x - 4)² + (y - 3)² = 36.
The "center" of circle is called as midpoint of diameter.
The "x-coordinate" of "mid-point" is = (4+4)/2 = 4, and
The "y-coordinate" of "mid-point" is = (9+(-3))/2 = 3.
So, center of circle is (4,3),
The radius of circle is half the length of the diameter, which is distance between two endpoints of diameter. We find distance using distance formula:
⇒ distance = √((x₂ - x₁)² + (y₂ - y₁)²), where (x₁,y₁) and (x₂,y₂) are "end-points" of diameter.
⇒ distance = √((4 - 4)² + (9 - (-3))²)
⇒ √(144) = 12.
So, radius is 6.
The equation of circle with center (h,k) and radius "r" is : ⇒ (x - h)² + (y - k)² = r²,
Substituting the values
We get,
⇒ (x - 4)² + (y - 3)² = 6²,
⇒ (x - 4)² + (y - 3)² = 36,
Therefore, the equation of the circle is (x - 4)² + (y - 3)² = 36.
Learn more about Circle here
https://brainly.com/question/29104982
#SPJ4
From his home, Reggie would have to walk due north to get to his friend Harry's house and
due east to get to his friend Albert's house. It is 1 mile from Reggie's house to Albert's house
and a straight-line distance of 5 miles from Harry's house to Albert's house. How far is
Reggie's house from Harry's house? If necessary, round to the nearest tenth.
Answers
Answer:
the distaance would be 4.9 miles
Step-by-step explanation:
You have to use pythagorean theorem. 5squared plus squared equals one squared. work this equation and you get 4.89 rounded its 4.9.
I need help with this, if anyone can I appreciate it. ✨

Answers
Answer:
85, -91
Step-by-step explanation:
Find the surface area of the net. HELP PLEASE!!! BRANLIEST
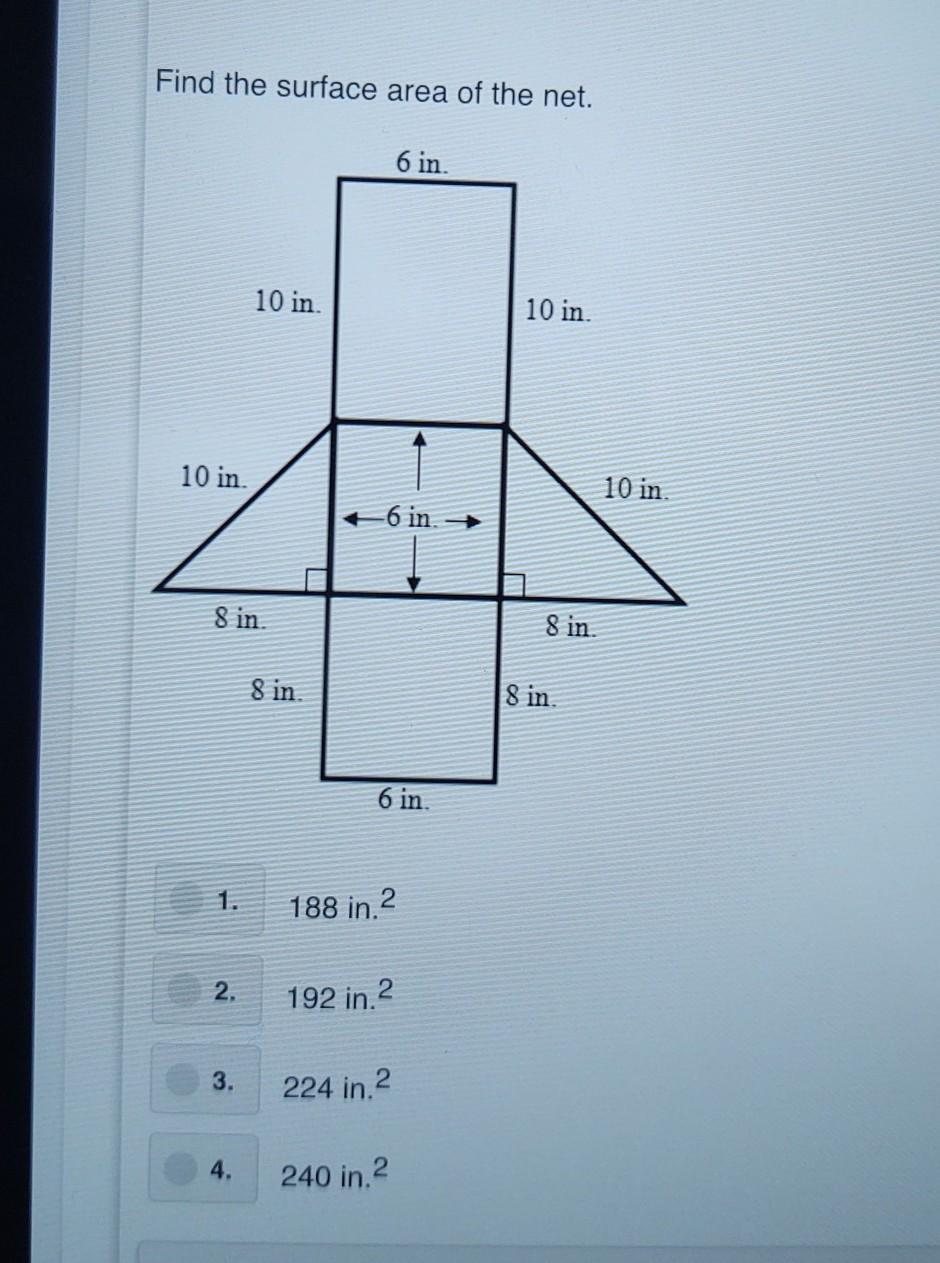
Answers
Answer:
2. 192 inches squared
Step-by-step explanation:
First find all the areas, then add them up
---------------------------------------------------------------------------------------------------------------
Have a good day :)
The first two terms of a sequence are a, = 3 and a₂=-1. Let a, be the third term when the sequence is
arithmetic and let b, be the third term when the sequence is geometric. What is the value of 2a,-3bg?

Answers
The value of 2a₃ - 3b₃ is -29/3.
How to find the value of 2a₃ - 3b₃?To find the value of 2a₃ - 3b₃, we shall find the third term of the arithmetic sequence and the third term of the geometric sequence.
Firstly, the third term of the arithmetic sequence:
We shall first determine the common difference (d) - the value that is constant, added to each term to get the next term.
Given:
a₁ = 3
a₂ = -1
The common difference (d):
d = a₂ - a₁
d = -1 - 3
d = -4
Next, the third term of the arithmetic sequence (a₃):
a₃ = a₂ + d
a₃ = -1 + (-4)
a₃ = -5
Secondly, the third term of the geometric sequence:
Here, we can get each term by multiplying the previous term by a common ratio (r).
Given:
a₁ = 3
a₂ = -1
The common ratio (r):
r = a₂ / a₁
r = -1 / 3
Then, the third term of the geometric sequence (b₃):
b₃ = a₂ * r²
b₃ = -1 * (-1/3)²
b₃ = -1 * (1/9)
b₃ = -1/9
Finally, we find the value of 2a₃ - 3b₃:
2a₃ - 3b₃ = 2(-5) - 3(-1/9)
2a₃ - 3b₃ = -10 + 3/9
2a₃ - 3b₃ = -10 + 1/3
2a₃ - 3b₃ = -30/3 + 1/3
2a₃ - 3b₃ = -29/3
Therefore, the value of 2a₃ - 3b₃ is -29/3.
Learn more about arithmetic sequence at brainly.com/question/26263191
#SPJ1
Question completion:
Your question is incomplete, but most probably your full question is:
The first two terms of a sequence are a₁ = 3 and a₂=-1. Let a₃ be the third term when the sequence is arithmetic and let b₃ be the third term when the sequence is geometric. What is the value of 2a₃-3b₃?
Write the multiplication table for Z3[x]/(x^2-x)
Answers
The elements of Z3[x]/(x^2 - x) are of the form ax + b that is multiplication table, where a and b are elements of Z3.
The multiplication table is:
| 0 1 x 1+x 2 2+x
-------------------------------
0 | 0 0 0 0 0 0
1 | 0 1 x 1+x 2 2+x
x | 0 x 2x 2+x x 1+2x
1+x| 0 1+x 2+x 2 2+x x
2 | 0 2 x 2+x 1 1+x
2+x| 0 2+x 1+2x x 1+x 2
Note that in this table, we use the fact that x^2 - x = 0, which implies that x^2 = x.
To know more about multiplication table,
https://brainly.com/question/30762398
#SPJ11
I need HELP PLEASE GIVE ME THE ANSWERS FAST I DONT HAVE MUCH
TIME!!!'
Suppose f'(2) = e- Evaluate: fe-- " sin(2f(x) + 4) dx +C (do NOT include a constant of integration)
Answers
The value of the integral ∫[e^(-sin(2f(x) + 4))] dx + C,
where f'(2) = e simplifies to f(x) + C
The integral of e^(-sin(2f(x) + 4)) with respect to x cannot be evaluated directly without knowing the specific form of f(x). However, we can use the fact that f'(2) = e to simplify the expression. Since f'(2) represents the derivative of f(x) evaluated at x = 2, we can rewrite it as follows:
f'(2) = e
f'(2) = e^(-sin(2f(2) + 4))
Now, let's denote 2f(2) + 4 as a constant c for simplicity. We can rewrite the equation as:
f'(2) = e^(-sin(c))
Integrating both sides of the equation with respect to x, we get:
∫[f'(2)] dx = ∫[e^(-sin(c))] dx
The integral of f'(2) with respect to x is simply f(x) + C, where C is the constant of integration. Therefore, the final answer to the integral expression is:
∫[e^(-sin(c))] dx = f(x) + C
In summary, the integral of e^(-sin(2f(x) + 4)) dx + C, given f'(2) = e, simplifies to f(x) + C.
Learn more about integration here:
https://brainly.com/question/31954835
#SPJ11
33.72 rounded to 1 decimal place
Answers
Answer:
33.7
Step-by-step explanation:
.72 is closer to .70 than .80
Four transformations of the function f(x)=2x−4 are given below. For each transformation, drag the expression that shows the result of that transformation into the box under it.
Answers
The given function f(x) = 2x - 4 undergoes four transformations: vertical stretch, vertical translation, horizontal reflection, and horizontal translation. The expressions representing each transformation are as follows:
The given function f(x) = 2x - 4 can be transformed in various ways. Let's analyze each transformation individually.
1. Vertical Stretch:
A vertical stretch multiplies the function's output (y-value) by a constant. In this case, the expression for the vertical stretch is:
f₁(x) = a * f(x)
where 'a' is the scaling factor. This transformation affects the function's steepness. If 'a' is greater than 1, the graph becomes steeper; if 'a' is between 0 and 1, the graph becomes flatter.
2. Vertical Translation:
A vertical translation shifts the function up or down by adding or subtracting a constant to the function's output (y-value). The expression for the vertical translation is:
f₂(x) = f(x) + b
where 'b' represents the amount of vertical shift. If 'b' is positive, the graph shifts upward; if 'b' is negative, the graph shifts downward.
3. Horizontal Reflection:
A horizontal reflection flips the function across the y-axis. The expression for the horizontal reflection is:
f₃(x) = -f(x)
This transformation changes the sign of the function's output for every input value, resulting in a mirror image of the original graph.
4. Horizontal Translation:
A horizontal translation shifts the function left or right by adding or subtracting a constant to the function's input (x-value). The expression for the horizontal translation is:
f₄(x) = f(x - c)
where 'c' represents the amount of horizontal shift. If 'c' is positive, the graph shifts to the right; if 'c' is negative, the graph shifts to the left.
To learn more about function click here: brainly.com/question/30721594
#SPJ11