Rewrite the following equation in standard form
y = 9x + 7
Answers
Answer:
9x - y = -7
Step-by-step explanation:
Related Questions
Please please please helppp!!! BRAINLIEST FOR CORRECT ANSWER! Erin made a mistake when writing a transformation rule to translate points 2 units up and 4 units to the left.
Transformation rule: (x, y) -> (x + 2, y - 4)
A. What is wrong with Erins transformation rule?
B. What is the correct transformation rule?
Answers
Answer:
a. The x and the y values are flipped, it reads left 2 down 4
b. it should be (x+4, y+2)
Step-by-step explanation:
when it is plus on x it is left and when it is negative on y it is down
A man buys a certain number of Litchies at 20 per rupee and equal number at 30 per rupee. He
oranges at 90 paisa each. If he plans to make a profit of
of the oranges ?
b)
mixed them and sold them at 25 per rupee. Find his gain or loss percent.
150/
If he sold it for Rs 81 less, his loss would have been
Answers
Full question :
A man buys a certain number of oranges at 20 for Rs. 60 and an equal number at 30 for Rs. 60. He mixes them and sells them at 25 for Rs. 60. What is the gain or loss percent?
Answer:
4% loss(percentage loss on cost price)
Step-by-step explanation:
we will be employing algebra in solving this problem :
20 oranges at 60 Rs=60Rs/20 per orange=3Rs per orange
Say x oranges bought at 3Rs per orange=3Rsx
Equal number of oranges at 30 oranges for 60 Rs=60Rs/30 per orange=2Rs per orange
Say x oranges bought at 3Rs per orange=2Rsx
Total Cost Price = 3Rsx + 2Rsx = 5Rsx
He then sells all oranges at 25 for 60 Rs
Therefore price per orange=60/25=12/5Rs
since he sold x+x oranges(from the above calculations)
Total selling price=total oranges *12/5Rs=2x oranges*12/5Rs=24x/5Rs
Profit or loss=24x/5-5x=-x/5
therefore we have a loss =-x/5
Percentage of loss(on cost price)
=x/5÷5x∗100=
=1/25∗100=4%
URGENT NEED HELP FAST

Answers
Answer: I think it’s the 4th one
Step-by-step explanation:
Answer:
2nd one
Step-by-step explanation:
Shaded below means less than
If ΔRST congruent to ΔNPQ, which of the following is true? A. ∠R congruent to ∠P B. ∠R congruent to ∠Q C. ∠T congruent to ∠P D. ∠T congruent to ∠Q

Answers
Answer:
Step-by-step explanation:
The order of the expression for congruent shapes indicate the
corresponding vertices between the two shapes that are congruent.
The option which is true is D. T = Q.
Reasons:
The given statement is; ΔRST ≅ ΔNPQ
By Corresponding Parts of Congruent Triangle are Congruent, CPCTC, we
have; The sides on ΔRST are congruent to the corresponding sides of ΔNPQ
Therefore;
RS ≅ NP
RT ≅ NQ
ST ≅ PQ
By CPCTC, we have that the angles on ΔRST are congruent to the corresponding angles of ΔNPQ
Therefore;
∠R ≅ ∠N
∠S ≅ ∠P
∠T ≅ ∠Q
Which gives, by definition of congruency;
∠R = ∠N
∠S = ∠P
∠T = ∠Q
Therefore, the true statement is D. T = Q.
give brainliest
A piece of string is 28 cm long. It is used to from a square. (a) what is the length of each side of square? (b) what is the area of the square.?
Answers
Answer:
7 cm and 49 cm²
Step-by-step explanation:
(a)
A square has 4 equal sides , then
28 cm ÷ 4 = 7 cm
The length of each side of the square is 7 cm
(b)
The area (A) of a square is
A = s² ( s is the side length ) , then
A = 7² = 49 cm²
Answer:
Step-by-step explanation:
Perimeter of square will be equal to the length of the string
Perimeter of square = 28 cm
4*side = 28
Divide both sides by 4
Side = 28/4
Side = 7 cm
b) Area of square = side * side
= 7 * 7
=49 cm²
23.A chef ordered 400 pounds of potatoes in same-sized bags. Which expressions show
the number of bags and number of pounds of potatoes per bag the chef may have
ordered? Choose all that apply.
E 50 x 80
80 x 5
B 10 x 40
0 20 x 20
© 20 x 20

Answers
Answer:
10*40
80*5
20*20
Step-by-step explanation:
20*20=400
80*5=400
10*40=400
Determine the equation of the line in slope-intercept form (y = mx + b).

Answers
Answer:
y=3x-12
Step-by-step explanation:
to find slope we use y2-y1/x2-x1 by using any 2 points on the graph
(0,-12) (4,0)
0-(-12)/4-0)
12/4
3
The slope is 3
The y intercept is -12 since it crosses the y axis when y=-12
So we write those is y=Mx+b format where m is the slope and b is the y intercept
y=3x-12
Hopes this helps please mark brainliest
In Problems 55-62, write each function in terms of unit step functions. Find the Laplace transform of the given function 0 =t< 1 57. f(t) = {8 12 1 Jo, 0 =t < 30/2 58. f(t) = ( sint, t = 30/2
Answers
The Laplace transform of the given function is,
L{f(t)} = (8/s) - 4e^{-3s/2}/s - 6e^{-2s}/s
Given function is f(t) = {8 12 1 Jo, 0 ≤ t < 3/2, 3/2 ≤ t < 2, 2 ≤ t < ∞ respectively.
We have to find Laplace transform of the given function.
For first interval 0 ≤ t < 3/2,
f(t) = 8u(t) - 8u(t-3/2)
For second interval 3/2 ≤ t < 2,
f(t) = 12u(t-3/2) - 12u(t-2)
For third interval 2 ≤ t < ∞,
f(t) = Jo(u(t-2))
Hence, we can write the Laplace transform of the given function as,
L{f(t)} = L{8u(t) - 8u(t-3/2)} + L{12u(t-3/2) - 12u(t-2)} + L{Jo(u(t-2))}
Where, L is Laplace transform.
Let's calculate each Laplace transform stepwise,
1. L{8u(t) - 8u(t-3/2)}L{8u(t)} = 8/L{u(t)}L{u(t)}
= 1/sL{u(t-3/2)}
= e^{-3s/2}/s
Therefore,
L{8u(t) - 8u(t-3/2)} = 8[1/s - e^{-3s/2}/s]
2. L{12u(t-3/2) - 12u(t-2)}L{12u(t-3/2)}
= 12e^{-3s/2}/sL{12u(t-2)}
= 12e^{-2s}/s
Therefore,
L{12u(t-3/2) - 12u(t-2)} = 12[e^{-3s/2}/s - e^{-2s}/s]
3. L{Jo(u(t-2))}L{Jo(u(t-2))} = ∫_{0}^{∞}δ(t-2)e^{-st}dtL{Jo(u(t-2))}
= e^{-2s}
Hence, the Laplace transform of the given function is,
L{f(t)} = 8[1/s - e^{-3s/2}/s] + 12[e^{-3s/2}/s - e^{-2s}/s] + e^{-2s}
= (8/s) - 4e^{-3s/2}/s - 6e^{-2s}/s
To know more about Laplace visit:
https://brainly.com/question/30759963
#SPJ11
Find the derivative of the function at the point p in the direction of a. f(x,y,z)=7x−10y+5z,p=(4,2,5),a= 7
3
i− 7
6
j− 7
2
k A) 7
71
B) 7
41
C) 7
101
D) 7
31
Answers
Answer:
Step-by-step explanation:
Correct answer : B
Answer:
The answer is B.
If no preliminary study is done, what size sample must be taken if the director is to say with 90% confidence that the sample estimate is within 2% of the population proportion
Answers
Find the equation of the hyperbola with the following properties. Express your answer in standard form.Foci at (7, 0) and (7, 10)Asymptotes ofy -5 = t;( -7

Answers
Answer:
\(\frac{(y-5)^2}{16}-\frac{(x-7)^2}{9}=1\)
Explanation:
The standard form of an hyperbola is:
\(\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1\)Where (h, k) are the coordinates of the center.
We are given the asyptotes and the foci.
The foci are (7, 0) and (7, 10)
The y value of the center of the parabola is midway from the two foci. Then, the y-coordinate of the center is 5
The coordinated of the center are (7, 5)
Now, we can use that the form of the asymptotes are:
\(y=k\pm\frac{a}{b}(x-h)\)We have:
\(y-5=\frac{4}{3}(x-7)\)Then:
\(\frac{a}{b}=\frac{4}{3}\)a = 4
b = 3
Now we can write:
\(undefined\)Write a variable expression to model real world situation.
A suit costs $65. Represent the cost of n suits.
Answers
$65 x n = $65n
For example, 3 suits will cost
$65 x 3 = $195.
what is the value of 2 3/4 ➗ 3/4
Answers
Answer:
3 2/3 is the answer
Step-by-step explanation:
Conversion a mixed number 2 3/
4
to a improper fraction: 2 3/4 = 2 3/
4
= 2 · 4 + 3/
4
= 8 + 3/
4
= 11/
4
To find new numerator:
a) Multiply the whole number 2 by the denominator 4. Whole number 2 equally 2 * 4/
4
= 8/
4
b) Add the answer from previous step 8 to the numerator 3. New numerator is 8 + 3 = 11
c) Write a previous answer (new numerator 11) over the denominator 4.
Two and three quarters is eleven quarters
Divide: 11/
4
: 3/
4
= 11/
4
· 4/
3
= 11 · 4/
4 · 3
= 44/
12
= 4 · 11 /
4 · 3
= 11/
3
Dividing two fractions is the same as multiplying the first fraction by the reciprocal value of the second fraction. The first sub-step is to find the reciprocal (reverse the numerator and denominator, reciprocal of 3/
4
is 4/
3
) of the second fraction. Next, multiply the two numerators. Then, multiply the two denominators. In the next intermediate step , cancel by a common factor of 4 gives 11/
3
.
so you simplify to get 3 2/3
the green goober, a wildly unpopular superhero, mixes 3 liters of yellow paint with 5 liters of blue paint to make 8 liters of special green paint for his costume.
Answers
Answer:
the answer would just be 8
Step-by-step explanation:
5 +3 = 8 and it would be a deep green
The position of a passenger train that is traveling at an initial speed of 14 feet per second and continues to accelerate can be modeled by the function: y = 14t2. a second train that is 1,200 feet ahead of the first train is traveling at a constant speed of 149 feet per second and can be modeled by the function: y = 149t 1200. solve the system of equations. which solution represents a viable time that the trains are side by side? a. 14 seconds b. 15 seconds c. 16 seconds d. 17 seconds
Answers
The trains are side by side after approximately 15 seconds.Option (b) is correct.
How to solve system of equation?The position of the first train is given by the function:
\($$y_1 = 14t^2$$\)
The position of the second train is given by the function:
\($$y_2 = 130t + 1200$$\)
To find the time when the trains are side by side, we need to solve for the value of t that makes y1 = y2. Thus, we can set the two equations equal to each other:
\($$14t^2 = 130t + 1200$$\)
Rearranging the terms, we get:
\($$14t^2 - 130t - 1200 = 0$$\)
Dividing both sides by 2 to simplify the coefficients, we get:
\($7t^2 - 65t - 600 = 0$$\)
We can use the quadratic formula to solve for t:
\($t = \frac{-(-65) \pm \sqrt{(-65)^2 - 4(7)(-600)}}{2(7)} = \frac{65 \pm \sqrt{4225 + 16800}}{14}$$\)
Simplifying the expression under the square root, we get:
\($$\sqrt{21025} = 145$$\)
So the solutions are:
\($t_1 = \frac{65 + 145}{14}=15$$\)
\($t_2 = \frac{65 - 145}{14} \approx -5.71$$\)
Since time cannot be negative, we discard t2 as an extraneous solution. Thus, the viable time when the trains are side by side is:
\($t = t_1 =15$$\)
Therefore, the trains are side by side after approximately 15 seconds.
To know more about Function visit:
brainly.com/question/28193995
#SPJ1
Help pleaseee
The figure

Answers
Answer:
the 4th one pentagonal prism
Answer:
pentagonal prism
Step-by-step explanation:
it doesn't resemble a pyramid, so it could only be a prism, and it isn't a rectangular one, cause it has two pentagons, on top and bottom
Determine if the series below converges or diverges using the alternating series test. If the alternating series test does not apply, use the nth term divergence test. ∑ n=1
[infinity]
ln(5n+2)
(−1) n
Select the correct answer below: The series converges. The series diverges.
Answers
The sequence {ln(5n+2)} approaches zero as n approaches infinity. Thus, the Alternating Series Test (AST) is verified.AST applies. Therefore, the given series converges.
The Alternating Series Test (AST) helps to determine the convergence of a series where the signs alternate. If the series satisfies the following conditions, then it converges:the terms are decreasing in absolute value,the series approaches zero and the terms are alternating in sign.The nth-term divergence test (NTDT) helps determine if a sequence or series is divergent if the sequence of the series does not converge to zero as n approaches infinity.The given series is ∑ n=1
[infinity]
ln(5n+2)
(−1) n
.Now, we will verify the condition of the Alternating Series Test (AST) and the nth term divergence test (NTDT).AST (1) The sequence {ln(5n+2)} is decreasing for all n ≥ 1.AST (2)
The sequence {ln(5n+2)} approaches zero as n approaches infinity.AST (3) The series is alternating. That is, it is of the form (-1)n.AST (1) and AST (2) are verified as follows:
AST (1) f(x) = ln(5x + 2)f'(x) = 5/5x + 2 < 0 for x ≥ 1, as (5x + 2) > 0 for x ≥ 1.
f(x) is a decreasing function for x ≥ 1. Therefore, the sequence {ln(5n+2)} is decreasing for all n ≥ 1.AST (2)
lim ln(5n + 2) = lim (ln(5n + 2))/(1/n) = lim (ln(5n + 2))/(1/n) = lim (ln(5 + 2/n))/(1/n) = l
im [(ln(5 + 2/n))/(1/n)] (5 + 2/n)^n
= e^7 and hence (ln(5n + 2))/
(1/n) --> 0 as n--> infinity
Therefore, the sequence {ln(5n+2)} approaches zero as n approaches infinity.Thus, the Alternating Series Test (AST) is verified.AST applies. Therefore, the given series converges.
To Know more about Alternating Series Test visit:
brainly.com/question/30400869
#SPJ11
please help!!!!! Need solvingg

Answers
Answer:
A, 22
Step-by-step explanation:
DOF-DOE=EOF
50-28=22 degrees
Answer:
A=22
Step-by-step explanation:
∠DOF=∠DOE+∠EOF
so ∠EOF=∠DOF-∠DOE=50°-28°=22°
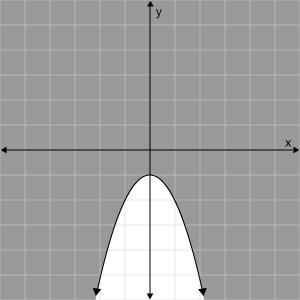
Which graph represents the inequality \(y\ge-x^2+1\)?



Answers
The graph of the given inequality y ≥ x² + 1 is a shaded region above the downward-facing parabola -x² + 1.
Hence, graph A represents the given inequality.
The inequality y ≥ x² + 1 represents a region in the coordinate plane where y is greater than or equal to the value of the function -x² + 1 for any given x. The graph of this inequality is a shaded region above the downward-facing parabola -x² + 1. The vertex of this parabola is located at the point (0,1), and as x moves away from 0, the value of the function becomes more negative.
Therefore, the shaded region includes all points (x, y) where y is greater than or equal to the y-value of the parabola at that x-value. The resulting graph is a curve that opens downward and flattens out at y=1 as x moves further away from 0.
Hence, the correct option is A.
To know more about inequality here
https://brainly.com/question/31434121
#SPJ1
find angle a given that a=18.2, angle b=62° and angle c=48°
Answers
Answer:
They only add up to 128.2, so if they are asking for the final angle to equal 180, then it would equal 51.8.
Hope that this helps!
Subtract 19 and 4, triple the difference, and then add
four-fifths.
Answers
Answer:
45.8
Step-by-step explanation:
I think that is the correct answer
Solve for x.
3x < 12
Answers
Answer:
X can be anything below 4
Answer:
x should be 1,2, or 3
Step-by-step explanation:
because if you take 3x4 it would be 12 (the same) so that's wrong. so it would have to be lower than that
PLEASE HELP ME I WILL GIVE BRAINLIEST!!
Which row of Pascal's Triangle should you use to expand the binomial (a + b)^4?
Answers
Answer:
Step-by-step explanation:
a + b)^6 will have 7 terms so you want row 6 of the triangle 1 6 15 20 15 6 1
so (a + b)^6 = a^6 + 6a^(5)b + 15a^(4)b^2 + 20a^(3)b^3 + 15a^(2)b^4 + 6ab^5 + b^6
given a = d and b = -5y
∴ (d − 5y)^6 = d^6 + 6d^(5)(-5y) + 15d^(4)(-5y)^2 + 20d^(3)(-5y)^3 + 15d^(2)(-5y)^4 +
match to form complementary angle pairs. sin(14) cos(37) sin(49) cos(66) sin(41) cos(24)
cos(76) —>
sin(66)—>
sin(53)—>
cos(49)—>
Answers
Answer:
see explanation
Step-by-step explanation:
using the cofunction identities
cos x = sin(90 - x)
sin x = cos(90 - x)
then
cos76° = sin(90 - 76)° = sin14°
sin66° = cos(90 - 66)° = cos24°
sin53° = cos(90 - 53)° = cos37°
cos49° = sin(90 - 49)° = sin41°
The Matched values are
cos(76) —> sin (14)
sin(66)—> cos (24)
sin(53)—> cos (37)
cos(49)—> sin (41)
What is Trigonometry?One area of mathematics known as trigonometry examines the relationship between the sides and angles of a right triangle. The relationship between sides and angles is defined for 6 trigonometric functions.
For complementary angle,
a+ b= 90
So, sin (14)
= cos (90 - 76)
= cos 76
and, cos (37)
=sin (90 - 53)
= sin (53)
and, sin (49)
= cos (90- 41)
= cos 41
and, cos (66)
= sin (90 - 24)
= sin 24
Then, the Matched values are
cos(76) —> sin (14)
sin(66)—> cos (24)
sin(53)—> cos (37)
cos(49)—> sin (41)
Learn more about Complementary Angle here:
https://brainly.com/question/26452063
#SPJ5
In regression analysis, the error term ε is a random variable with a mean or expected value of.
Answers
In regression analysis , the error term ε is a random variable with expected value of 0.
What is regression analysis?
A set of statistical procedures known as regression analysis is used to estimate the relationships between a dependent variable and one or more independent variables.
Main Body:
In regression analysis, the model in the form is called regression model.
The mathematical equation relating the independent variable to the expected value of the dependent variable; that is, E(y) = β0 + β1x, is known as regression equation.
So the answer to error term is 0.
To learn more about regression analysis click on the link below
https://brainly.com/question/28178214
#SPJ4
(1 point) find the solution to the linear system of differential equations {x′y′==−12x−30y3x 7y satisfying the initial conditions x(0)=26 and y(0)=−8.
Answers
The solution to the system of differential equations is: \(y(t) = -8 e^{(7t)}\)
We are given the system of differential equations:
\(x' = -12x - 30y^3\)
y' = 7y
To solve this system, we can use the method of elimination. First, we eliminate x from the first equation by differentiating both sides with respect to t:
\(x'' = -12x' - 30y^{3y'\)
Substituting the expression for y' from the second equation, we get:
\(x'' = -12x' - 210y^4\)
Now we have a second-order differential equation for x. To solve this equation, we first find the characteristic equation:
\(r^2 + 12r + 210 = 0\)
Using the quadratic formula, we get:
\(r = (-12 + \sqrt{(12^2 - 41210))} / (2\times 1) = -6 + 9i\)
Therefore, the general solution for x is:
\(x(t) = c1 e^{(-6t)} cos(9t) + c2 e^{(-6t)} sin(9t)\)
To find the values of c1 and c2, we use the initial condition x(0) = 26:
c1 = x(0) / cos(0) = 26
Next, we need to find x'(0) to determine c2. Differentiating the expression for x(t), we get:
\(x'(t) = -6c1 e^{(-6t)} cos(9t) - 9c1 e^{(-6t)} sin(9t) + c2 e^{(-6t)} cos(9t) - 6c2 e^{(-6t) }sin(9t)\)
Evaluating this expression at t=0 and using the initial condition \(x'(0) = -1226 - 30(-8)^3\), we get:
-6c1 + c2 = -2088
Therefore, c2 = -2088 + 6c1 = -2088 + 6(26) = -1952
Now we can write the solution for x as:
\(x(t) = 26 e^{(-6t)} cos(9t) - 1952 e^{(-6t)} sin(9t)\)
To find the solution for y, we use the second equation:
\(y(t) = c3 e^{(7t)\)
Using the initial condition y(0) = -8, we get:
c3 = y(0) = -8
Therefore, the solution to the system of differential equations is:
\(x(t) = 26 e^{(-6t)} cos(9t) - 1952 e^{(-6t)} sin(9t)\\y(t) = -8 e^{(7t)}\)
for such more question on differential equations
https://brainly.com/question/25731911
#SPJ11
A simple random sample of size n is drawn from a population that in normally distributed. The sample mean, is found to be 100, and the sample stamdard deviation is found to be 8.
Construct a 98% confidence interval about µ, if the samplesize n, is 20,
Lower bound: _______ Upper bound: ____________
(Round to one decimal place as needed
Answers
As per the confidence interval, Lower Bound is 94.874 and the Upper Bound is 105.126
Sample Mean = 100
Sample Standard Deviation = 8
Sample Size = 20
Calculating the confidence interval -
Confidence Interval = Sample Mean ± (Critical Value) x (Standard Deviation / √(Sample Size))
Substituting the values
= 100 ± (2.860) x (8 / √20)
= 100 ± 2.860 x (8 / 4.472)
= 100 ± 2.860 x 1.789
= 100 ± 5.126
Calculating the lower bound -
Lower Bound = 100 - 5.126 = 94.874
Calculating the upper bound -
Upper Bound = 100 + 5.126 = 105.126
Read more about confidence interval on:
https://brainly.com/question/20309162
#SPJ4
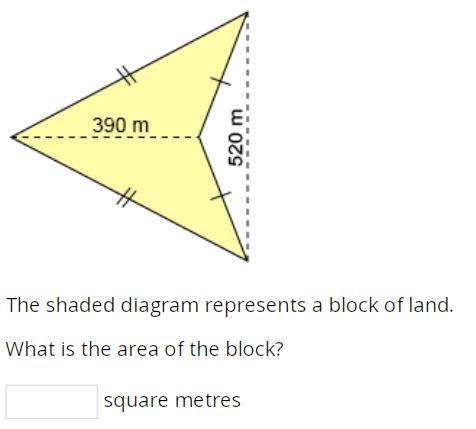
The shaded diagram represents a block of land.
What is the area of the block?
Answers
By using Heron's formula and standard formula for the area of a triangle, the area of the composite figure is 921006.497 square meters.
What is the area of a composite figure?
In this problem we must determine the area of a composite figure, which consists in subtracting the area of an isosceles triangle from the area of the equilateral triangle:
Big triangle
The area of the big triangle is determined by Heron's formula:
s = [3 · (520 m)] / 2
s = 780 m
A = √[(780 m) · (1560 m - 520 m)³]
A ≈936693.077 m²
Small triangle
H = (520 m) · sin 60°
H ≈ 450.333 m
h = 450.333 m - 390 m
h = 60.333 m
A = 0.5 · (520 m) · (60.333 m)
A = 15686.580 m²
Then, the area of the composite figure is 921006.497 square meters.
To learn more on Heron's formula: https://brainly.com/question/20934807
#SPJ1
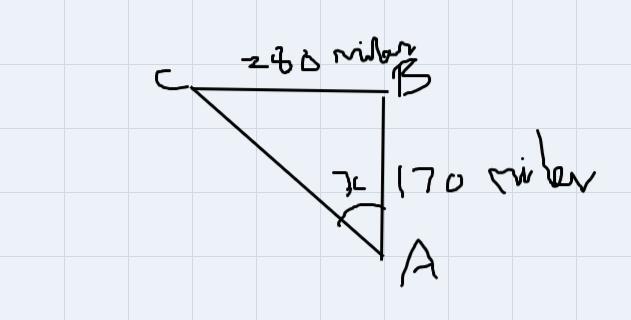
As seen in the accompanying diagram, a person can travel from New York City to Bufalo by going north 170 miles to Albany and then west 280 miles to Buffalo Buffalo If an engineer wants to design way to connect New York City directly to Buffalo what angle, would she need to build the highway? Find the angle to the nearest degree. To the serie how many miles would be saved by traveling directly from New York City to Buffalo rather than by traveling first to Albany and then to Buffalo

Answers
Anglex is 58.74 degre.
Miles saved by travelling in highways is 122.43 miles.
Given:
Distance between New York to Alban is 170 miles.
Distance between Alban to Baffalo is 280 miles.
The objective is to find the angle of highway to be built directly from New York to Buffalo. and also the difference in mile between the two routes.
The given image can be represented as,
In the obtained triangle right angled at B, as angle is required at A, then AC represents the hypotenuse side, AB represents the adjacent side and BC represents the opposite side.
Now,the angle can be calculated by the opposite side and adjacent side using tan theta.
\(\begin{gathered} \tan \theta=\frac{opposite}{adjacent} \\ \tan x=\frac{280}{170} \\ x=\tan ^{-1}(\frac{280}{170}) \\ x=59^0 \end{gathered}\)Now, the difference between the two routes can be calculated using Pythagorean theorem of the right triangle.
\(\begin{gathered} \text{Hypotenuse}^2=Opposite^2+Adjacent^2 \\ AC^2=BC^2+AC^2 \\ AC^2=280^2+170^2 \\ AC^2=78400+28900 \\ AC^2=107300 \\ AC=\sqrt[]{107300} \\ AC=327.57\text{ miles} \end{gathered}\)Thus the distance of highways directly from New york to Buffalo is 327.57 miles.
Now, consider D as the difference miles that would be saved by traveling directly from New York City to Buffalo
Then, the miles saced by travelling in this highway is,
\(\begin{gathered} D=(AB+BC)-AC \\ D=(280+170)-327.57 \\ D=450-327.57 \\ D=122.43\text{ miles} \end{gathered}\)Hence, the angle required to build the highway is 59 degree. And by traveling in this highway directly from New york city to Buffalo will save 122.43 miles.
how many cubes with side links of 1/2 cm does it take to fill the prism
Answers
To determine the number of cubes needed to fill a prism, we need additional information about the dimensions of the prism.
The number of cubes required to fill a prism depends on the dimensions of the prism, specifically its length, width, and height. Without knowing these dimensions, we cannot calculate the exact number of cubes needed.
For example, if the prism has a length of 10 cm, a width of 5 cm, and a height of 8 cm, and the side length of each cube is 1/2 cm, we can calculate the number of cubes as follows:
Volume of the prism = length x width x height = 10 cm x 5 cm x 8 cm = 400 cm³
Volume of each cube = side length x side length x side length = (1/2 cm) x (1/2 cm) x (1/2 cm) = 1/8 cm³
Number of cubes needed = Volume of prism / Volume of each cube = 400 cm³ / (1/8 cm³) = 3200 cubes
Therefore, it would take 3200 cubes with a side length of 1/2 cm to fill the given prism, assuming it has the specified dimensions.
Learn more about Volume of prism here:
https://brainly.com/question/13338592
#SPJ11
To accurately determine the number of cubes required to fill the prism, we need the dimensions (length, width, and height) of the prism. Once we have the specific measurements, we can proceed with the calculation.