Read the following description of a relationship:
The maple tree in Maggie's backyard is 5 years younger than the willow tree.
Let w represent the willow tree's age and m represent the maple tree's age.
Use the function m = w- 5 to find the value of m when w = 6.
m =
Answers
Answer:
The Answer is 1
Step-by-step explanation:
W = 6
Then it would be...
6-5 = 1
Related Questions
3. An investor plans to invest $500/year and expects to get a 10.5% return. If the investor makes these contributions at the end of the next 20 years, what is the present value (PV) of this investment today?
Answers
The present value (PV) of the investment today is approximately $2,965.05.
To find the present value (PV) of the investment today, we need to calculate the present value of each individual contribution and then sum them up. We can use the formula for the present value of an annuity to do this calculation.
The formula for the present value of an annuity is given by:
PV = C * [(1 - (1 + r)^(-n)) / r]
Where:
PV = Present Value
C = Cash flow per period
r = Interest rate per period
n = Number of periods
In this case, the cash flow per period (C) is $500, the interest rate per period (r) is 10.5% (or 0.105), and the number of periods (n) is 20 years.
Let's plug in these values into the formula and calculate the present value (PV):
PV = $500 * [(1 - (1 + 0.105)^(-20)) / 0.105]
Using a calculator, we can evaluate the expression inside the brackets:
PV = $500 * [(1 - 0.376889) / 0.105]
Simplifying further:
PV = $500 * [0.623111 / 0.105]
PV = $500 * 5.930105
PV = $2,965.05
Therefore, the present value (PV) of the investment today is approximately $2,965.05.
for such more question on present value
https://brainly.com/question/28256489
#SPJ8
Sean and Ezra have a total of $240. Sean and Kezia have a total of $360. The ratio of Ezra's amount to Kezia's amount is 1 : 4. How much money does Sean have?
Answers
240/4
$60
B.$360*1/4
$360/4
$90
6x^-2
f^-1g^-1
y^-3
5^-3
3^-2
(-2)^-3
Answers
Answer:
6/x^2
1/(fg)
1/y^3
1/125.
1/9
-1/8
Step-by-step explanation:
6x^-2 can be simplified to 6/x^2, since a negative exponent means "inverse".
f^-1g^-1 can be simplified to 1/(fg), since a negative exponent means "inverse".
y^-3 can be simplified to 1/y^3, since a negative exponent means "inverse".
5^-3 can be simplified to 1/5^3, which is equal to 1/125.
3^-2 can be simplified to 1/3^2, which is equal to 1/9.
(-2)^-3 can be simplified to -1/2^3, which is equal to -1/8. When a negative exponent is applied to a negative base, it is important to remember that the negative sign remains.
An ant colony is built by 200 ants. The number of ants triples each week. How many ants will be in the colony at the end of the eighth week?
Answers
N = N0 * 3^t
where N is the final number of ants, N0 is the initial number of ants, 3 is the rate of growth (since the number of ants triples each week), and t is the number of weeks.
We are given that there are initially 200 ants, so N0 = 200. We want to find N at the end of 8 weeks, so t = 8. Substituting these values into the formula, we get:
N = 200 * 3^8
N = 200 * 6561
N = 1,312,200
Therefore, at the end of the eighth week, there will be 1,312,200 ants in the colony.
Below are two parallel lines with a third line intersecting them. 122
Answers
The value of angle x based on the information will be 131°.
How to calculate the valueAlternate interior angles are the angles formed when a transversal intersects two coplanar lines.
The two marked angles are on opposite sides of the transversal, so they are called "alternate" angles. They are both between the parallel lines, so they are called "interior" angles.
In this geometry, alternate interior angles are congruent. They have the same measure. x° = 131°.
Learn more about angles on:
https://brainly.com/question/25716982
#SPJ1

A map uses a scale of 1
cm = 5½ miles. In actual
distance, the entrances to
two parks are 24 miles
apart. How far apart are
they on the map?
Answers
Answer:
3.36 cm
Step-by-step explanation:
24 - 5 1/2 = 18.5
To find the distance on the map, we can set up a proportion:
1 cm / 5.5 miles = x cm / 18.5 miles
5.5 times 37/11 equals to 18.5; 1 times 37/11 is approximately equals to 3.36 cm (rounded to the nearest hundredths).
NO LINKS!! URGENT HELP PLEASE!!!
11. Write the equation for the graph

Answers
This is the same as writing y = sqrt(4(x+5)) - 1
===============================================
Explanation:
The given graph appears to be a square root function.
The marked points on the curve are:
(-4,1)(-1,3)(4,5)Reflect those points over the line y = x. This will have us swap the x and y coordinates.
(-4,1) becomes (1,-4)(-1,3) becomes (3,-1)(4,5) becomes (5,4)Recall the process of reflecting over y = x means we're looking at the inverse. The inverse of a square root function is a quadratic.
----------
Let's find the quadratic curve that passes through (1,-4), (3,-1) and (5,4).
Plug the coordinates of each point into the template y = ax^2+bx+c.
For instance, plug in x = 1 and y = -4 to get...
y = ax^2+bx+c
-4 = a*1^2+b*1+c
-4 = a+b+c
Do the same for (3,-1) and you should get the equation -1 = 9a+3b+c
Repeat for (5,4) and you should get 4 = 25a+5b+c
We have this system of equations
-4 = a+b+c-1 = 9a+3b+c4 = 25a+5b+cUse substitution, elimination, or a matrix to solve that system. I'll skip steps, but you should get (a,b,c) = (1/4, 1/2, -19/4) as the solution to that system.
In other words
a = 1/4, b = 1/2, c = -19/4
We go from y = ax^2+bx+c to y = (1/4)x^2+(1/2)x-19/4
----------
Next we complete the square
y = (1/4)x^2+(1/2)x-19/4
y = (1/4)( x^2+2x )-19/4
y = (1/4)( x^2+2x+0 )-19/4
y = (1/4)( x^2+2x+1-1 )-19/4
y = (1/4)( (x^2+2x+1)-1 )-19/4
y = (1/4)( (x+1)^2-1 )-19/4
y = (1/4)(x+1)^2- 1/4 - 19/4
y = (1/4)(x+1)^2 + (-1-19)/4
y = (1/4)(x+1)^2 - 20/4
y = (1/4)(x+1)^2 - 5
The equation is in vertex form with (-1,-5) as the vertex. It's the lowest point on this parabola. Placing it into vertex form allows us to find the inverse fairly quickly.
----------
The last batch of steps is to find the inverse.
Swap x and y. Then solve for y.
y = (1/4)(x+1)^2 - 5
x = (1/4)(y+1)^2 - 5
x+5 = (1/4)(y+1)^2
(1/4)(y+1)^2 = x+5
(y+1)^2 = 4(x+5)
y+1 = sqrt(4(x+5))
y = sqrt(4(x+5)) - 1
I'll let the student check each point to confirm they are on the curve y = sqrt(4(x+5)) - 1.
You can also use a tool like GeoGebra to verify the answer.
Sketch and label a net of the right triangular prism. Each square on the grid represents
1 square centimeter. Calculate the surface area of the prism by using its net.

Answers
The total surface area of the prism is determined as 216 cm².
What is the surface area of the prism?The surface area of the prism is calculated by applying the following formula.
The area of the two triangular faces is calculated as follows;
Area of the two triangles = 2 (¹/₂ x base x height )
Area of the two triangles = 2 (¹/₂ x 6 cm x 4 cm )
Area of the two triangles = 24 cm²
The area of rectangular faces is calculated as follows;
A = ( 5 cm x 12 cm ) + (5 cm x 12 cm ) + ( 6 cm x 12 cm )
A = 192 cm²
The total surface area of the prism is calculated as follows;
Area = 24 cm² + 192 cm²
Area = 216 cm²
The sketch of the triangular prism is in the image attached.
Learn more about surface area of prism here: https://brainly.com/question/16421693
#SPJ1

Of(x) = x² - 6x-1-
Mark thic and return
24
-10-8-8-22-
-8
-8
-10
2
B
8 10 x
What is the axis of symmetry
Answers
The axis of symmetry of the function f(x) = x² - 6x-1 is equal to 3.
How to determine the axis of symmetry of a quadratic function?In Mathematics, the axis of symmetry of a quadratic function can be calculated by using this mathematical equation:
Axis of symmetry, Xmin = -b/2a
Where:
a and b represents the coefficients of the first and second term in the quadratic function.
By substituting the parameters, we have the following:
Axis of symmetry, Xmin = -b/2a
Axis of symmetry, Xmin = -(-6)/2(1)
Axis of symmetry, Xmin = 6/2
Axis of symmetry, Xmin = 3.
Read more on quadratic functions here: brainly.com/question/14201243
#SPJ1
Find the distance between the point (2,1) and the line 3x- 4y+15=0
Answers
Answer:
Step-by-step explanation:
3
x
−
4
y
+
15
=
0
.
y
=
3
4
x
−
1
2
Correct answers 5.4
Distance from point (2,3) to the line 3x+4y+9=0
=>r=
3
2
+4
2
∣3(2)+4(3)+9∣
=>r=
9+16
∣16+12+9∣
=>r=
5
27
=>r=5.4
20 points
Use Pythagoras' theorem to work out the
height of the equilateral triangle below.
Give your answer in centimetres
(cm)

Answers
Answer:
9 × √3 cm or approximately 15.59 cm
Step-by-step explanation:
(look at the picture)

50 points and a BRAINLIEST if you answer correctly! Pls Pls help!

Answers
Answer:
3/10
Step-by-step explanation:
Numbers Given are:
1 1/2, 2 1/2, 1 2/3, and 2 5/6
The result at the end of all the math is 2 5/6.
1 2/3 + 2 5/6 = 4 1/2
Divide 4 1/2 by 1 2/3 to get 2 7/10.
Subtract 2 2/3 from 2 7/10 to get 1/5.
Multiply 1/5 by 1 1/2 to get 3/10.
So the number they thought of was 3/10.
The area of a rectangle is represented by the expression 2x2+3x−14. Factor this expression.(1 point)
(2x+4)(x−3)
(x+4)(x−3)
(2x+7)(x−2)
(x+7)(x−2)
Answers
Answer:
(2x+7)(x−2)
Step-by-step explanation:
In 1900 Kansas City had a population of 163,000In 2020 it has a population of 1,686,000Show me exponential growthHow many years after 1900Did it take for the population to double
Answers
The exponential growth is 1.95% and after 35.72 years the population will double.
What is an exponential function?It is defined as the function that rapidly increases and the value of the exponential function is always a positive. It denotes with exponent \(\rm y = a^x\)
where a is a constant and a>1
Let's suppose the exponential growth function is:
\(\rm y = Ae^{rt}\)
A = 163,000
y = 1,686,000
t = 2020 – 1900 = 120 years
Plug all the values in the function:
\(\rm 1686000 = 163000e^{120r}\)
\(\rm e^{120r} = 10.343\)
Taking ln both side and solving:
r = 0.0194
r = 1.946 ≈ 1.95%
\(\rm 2A = Ae^{0.0194t}\) (the population to double)
After solving:
t = 35.72 years
Thus, the exponential growth is 1.95% and after 35.72 years the population will double.
Learn more about the exponential function here:
brainly.com/question/11487261
#SPJ1
Identify the factors in the expression 5(m - 1). O A. 5 and (m - 1) O B. 5 and 1 1 O C. 5 and m O D. mand 1

Answers
Answer:
A. 5 and (m - 1)Step-by-step explanation:
Given expression:
5(m - 1)It is the product of two factors, in other words it has two factors:
5 and (m - 1)Correct choice is A
Step-by-step explanation:
Given expression = 5(m - 1)
5(m - 1) = 0
So, the factors are
5 and (m - 1)
A store had 40 cases of pop on hand at the beginning of the week and bought 120 cases from the vendor during the weed and had 63 cases on hand at the end of the week How many cases did the store sell for the week ?
Answers
Store sell 97 cases of pop for the week.
What is selling?" Selling is defined as the transactions done by a vendor in exchange of certain amount of money fixed on it."
According to the question,
Number of cases of pop at the beginning of the week = 40
Number of cases bought from the vendor = 120
Number of cases on hand at the end of the week = 63
Total number of cases in the store = 40 + 120
= 160
Number of cases store sell for the week = 160 - 63
= 97 cases
Hence, store sell 97 cases of pop for the week.
Learn more about selling here
https://brainly.com/question/22521384
#SPJ2
I am lost on this question i found both but it keeps on telling me i am incorrect

Answers
Answer:
I have completed the answers and attached them to the explanation.
Step-by-step explanation:

Answer:
Step-by-step explanation:
The question asks for a subtraction expression:
length is always a positive number so bigger number first here.
OB = 4-(-1) >only moves in x direction so subtract x's
AB = 4-(-2) >only moves in y direction so subtract y's
I need to find the missing angles

Answers
Answer:
g=93 h=87 k=122 m=58
Step-by-step explanation:
ADE and ABC are similar which best explains why the slope of the line between points a and D is the same as the slope between points a and B I ready diagnostic
Answers
If you flip two coins 68 times, what is the best prediction possible for the number of times both coins will land on heads?the number of times it will land on tails?
Answers
If you flip two coins 68 times, the best prediction for the number of times both coins will land on heads is 17.
If you flip two coins 68 times, the best prediction for the number of times both coins will land on tails is 17.
What is the probability of getting two heads?The possible outcomes when two coins are flipped are;
head - head = HH
tail - tail = TT
Head and tail = HT
Tail and head = TH
The probability of getting two heads = 1/4
If you flip two coins 68 times, the best prediction for the number of times both coins will land on heads is calculated as;
Expected value = (68 flips) x (1/4 probability of getting HH) = 17
The probability of getting two tails = 1/4
Expected value = 68 x 1/4 = 17
Learn more about probability here: https://brainly.com/question/24756209
#SPJ1
Does pi go on infinitely?
Answers
Answer:
Yea it does
Step-by-step explanation:
julia needs to make 500 hamburgers for the a school function... hamburger patties are sold in packets of 12
how many packets of patties should she buy ?
Answers
Julia needs to buy 42 packets of patties to make 500 hamburgers for the school function
What is an equation?An equation is an expression that shows how two or more numbers and variables are related using mathematical operations of addition, subtraction, multiplication, division, exponents and so on.
Hamburger patties are sold in packets of 12. Let x represent the number of packet of patties to be bought to make 500 hamburgers. Hence:
12x = 500
x = 500/12
x = 41.67
x≅ 42
Julia needs to buy 42 packets
Find more on equation at: https://brainly.com/question/2972832
#SPJ1
Please need help on this

Answers
Answer:
1) x² + 4x +1 = 1 (You have to put in +1)
2) True
Step-by-step explanation:
1)
2) A range is a representation of values between two points. When you're calculating the range of a parabola, you only know one of those points to start with. Your parabola will go on forever either up or down, so the end value of your range is always going to be ∞ (or −∞ if your parabola faces down.)
Answer: the answer is true
Step-by-step explanation: There are an infinite amount of numbers the parabola can hit, and there is no limit
hence the statement is true
Which statement is true in the question below?

Answers
Answer:B
Step-by-step explanation:
A group of students at a high school took a standardized test. The number of students who passed or failed the exam is broken down by gender in the following table. Determine whether gender and passing the test are independent by filling out the blanks in the sentence below, rounding all probabilities to the nearest thousandth.
Passed Failed
Male 17 6
Female 34 12
Since P(mail |fail)=________ and P(male)=______, the two results are_____ so the events are________
Answers
Answer:
Step-by-step explanation:
From the given information:
Passed Failed Total
Male 17 6 23
Female 34 12 46
Total 51 18 69
\(P(male | fail) = \dfrac{P(male \cap fail)}{ P(fail)}\)
\(P(male | fail) = \dfrac{\dfrac{6}{69} }{\dfrac{18}{69}}\)
\(P(male| fail) = \dfrac{1}{3}\)
\(P(male | fail) = 0.333\)
\(P(male) = \dfrac{23}{69}\)
\(P(male) = \dfrac {1}{3}\)
\(P(male) = 0.333\)
The two results are equal:
So the events are dependent.
Save Sut Henry hace entregas de la torta para una panaderia local Él les cobra una tarifa diaria de $ 25 más $ 5 por entrega. Él hizo 27 entregas hoy y está tratando de calcular cuánto le deben. Para el cálculo de su salario, la panadería se multiplica 25 x 5 y luego añade 27. Es cierto? B) No: que debería haber añadido 27, 25 y 5. No que debería haber multiplicado 27 por 5 y luego añadir 25 DO Nor que debería haber multiplicado 27 5 y luego resta 25.
Answers
Dado que el repartidor cobra $5 por cada entrega e hizo 27 entregas en el día, la panadería debería multiplicar 27 por 5. Además, el repartidor cobra una tarifa diaria de $25, así que se tendría que multiplicar 27 por 5 y luego añadir 25 para calcular su salario del día.
Por lo tanto, la respuesta correcta es la segunda opción:
Debería haber multiplicado 27 por 5 y luego añadir 25.
Find the area of the green region in the circle to the nearest tenth

Answers
The area of the green region of the circle is 96.4 ft².
What is area?Area is the region bounded by a plane shape.
To calculate the area of the green region of the circle, we use the formula below
Formula:
A = πr²∅/360Where:
A = Area of the green regionr = Radius of the circle∅ = Angle of the sector at the center of the circleFrom the diagram,
Given:
r = 17/2 = 8.5 feet∅ = (180-27°) = 153°π = 3.14Substitute these values into equation 1
A = 3.14×8.5²×153/360A = 96.4 ft²Learn more about area here: https://brainly.com/question/28470545
#SPJ1
The area of the green region in the circle given is expressed as approximately: a. 96.5 square feet.
How to Find the Area of a Sector in a Circle?The sector of a circle is calculated as:
A = ∅/360 * πr², where r is the radius and ∅ is the reference or central angle of the sector.
Given the following:
Central or reference angle (∅) = 180 - 27 = 153 degrees
Radius (r) = 17/2 = 8.5 feet
Plug in the values:
Area of the green region = 153/360 * π * 8.5²
Area of the green region ≈ 96.5 square feet.
Learn more about the sector of a circle on:
https://brainly.com/question/30507760
#SPJ1
Classify the relationship between each pair of angles as alternate interior, alternate exterior, corresponding, or consecutive interior angles.A. right angle 7 and right angle 9B. right angle 2 and right angle 8

Answers
A. The angles 7 and 9 are are alternate interior angles.
B. The angle 2 and 8 are are alternate exterior angles.
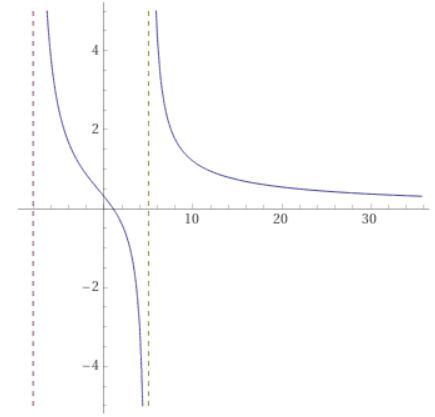
Answer questions: 1.1 x-intercepts y-intercept and vertical asymptotes Then 1.2 the domain and range 1.3 other asymptote and the end behavior

Answers
Given the Rational Function:
\(f(x)=\frac{12\mleft(x-1\mright)}{\mleft(x-5\mright)\mleft(x+8\mright)}\)(1.1) You can rewrite it in this form:
\(y=\frac{12(x-1)}{(x-5)(x+8)}\)• By definition, the x-value is zero when the function intersects the y-axis. Therefore, you need to substitute this value into the equation and then evaluate, in order to find the y-intercept:
\(x=0\)Then, you get:
\(y=\frac{12(0-1)}{(0-5)(0+8)}=\frac{12(-1)}{(-5)(8)}=\frac{-12}{-40}=\frac{3}{10}=0.3\)As an ordered pair, this is:
\((0,0.3)\)• In order to find the x-intercept, you need to substitute this value into the function and solve for "x", because the y-value is zero when the function intersects the x-axis:
\(y=0\)Then, you get:
\(\begin{gathered} 0=\frac{12(x-1)}{(x-5)(x+8)} \\ \\ 0=12(x-1) \\ \\ \frac{0}{12}=x-1 \\ \\ 0=x-1 \\ x=1 \end{gathered}\)As an ordered pair, this is:
\((1,0)\)• In order to find the Vertical asymptote, you need to make the denominator equal to zero and solve for "x":
\((x-5)(x+8)=0\)Notice that you get two Vertical Asymptotes:
\(\begin{gathered} x=5 \\ x=-8 \end{gathered}\)(1.2) By definition, the Domain of a function is the set of all the possible input values for which the function is defined.
Rational Functions are not defined for those numbers that make the denominator equal to zero. If you make the equation equal to zero and solve for "x", you get:
\((x-5)(x+8)=0\Rightarrow\begin{cases}x=5 \\ x=-8\end{cases}\)Therefore:
\(Domain\colon(-\infty,-8)\cup(-8,5)\cup(5,\infty)\)By definition, the Range is the set of all the possible output values of the function. For Rational Functions, the Range of the Rational Function is the Domain of its inverse.
In this case, you can find the inverse of the given function as follows.
- Solve for "x":
\(y(x-5)(x+8)=12(x-1)\)\(\begin{gathered} y(x^2+3x-40)=12x-12 \\ \\ yx^2+3xy-40y=12x-12 \end{gathered}\)\(yx^2+(3y-12)x-40y+12=0\)Applying the Quadratic Formula:
\(x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\)Where:
\(\begin{gathered} a=y^2 \\ b=3y-12 \\ c=-40y+12 \end{gathered}\)You get:
\(x=\frac{-(3y-12)\pm\sqrt[]{(3y-12)^2-4(y^2)(-40y+12)}}{2\cdot y^2}\)\(x=\frac{-(3y-12)\pm\sqrt[]{(3y-12)^2-4(y^2)(-40y+12)}}{2y^2}\)- Interchange the variables:
\(y=\frac{-(3x-12)\pm\sqrt[]{(3x-12)^2-4(x^2)(-40x+12)}}{2x^2}\)Notice that:
\(\begin{gathered} 2x^2=0 \\ x=0 \end{gathered}\)Hence, the Range of the original function is:
\(Range\colon(-\infty,\infty)\)(1.3) By definition, if the degree of the numerator is less than the degree of the denominator, the Horizontal Asymptote is:
\(y=0\)In this case, you can identify that the degree of the numerator is 1 and the degree of the denominator is 2:
\((x-5)(x+8)=(x)(x)+(x)(8)-(5)(x)-(5)(8)=x^2+8x-5x-40=x^2+3x-40\)Therefore, the Horizontal Asymptote is:
\(y=0\)By definition, the Horizontal Asymptote indicates the end behavior of the Rational Function. In this case, it indicates that:
\(f\mleft(x\mright)\to0\text{ as }x\rightarrow\pm\)(1.4) Knowing all the data of the function, you can graph it:
Hence, the answers are:
(1.1) x-intercept:
\((1,0)\)y-intercept:
\((0,0.3)\)Vertical Asymptotes:
\(\begin{gathered} x=5 \\ x=-8 \end{gathered}\)(1.2) Domain:
\(Domain\colon(-\infty,-8)\cup(-8,5)\cup(5,\infty)\)Range:
\(Range\colon(-\infty,\infty)\)(1.3)
Other Asymptote:
\(y=0\text{ (Horizontal Asymptote)}\)End Behavior:
\(\begin{gathered} As\text{ }x\rightarrow-\infty,f(x)\to0 \\ As\text{ }x\rightarrow\infty,f(x)\to0 \end{gathered}\)(1.4)

FInd the unknown value of:
18 = 3 + x
x = ?
Answers
the answer to the equation is x=15