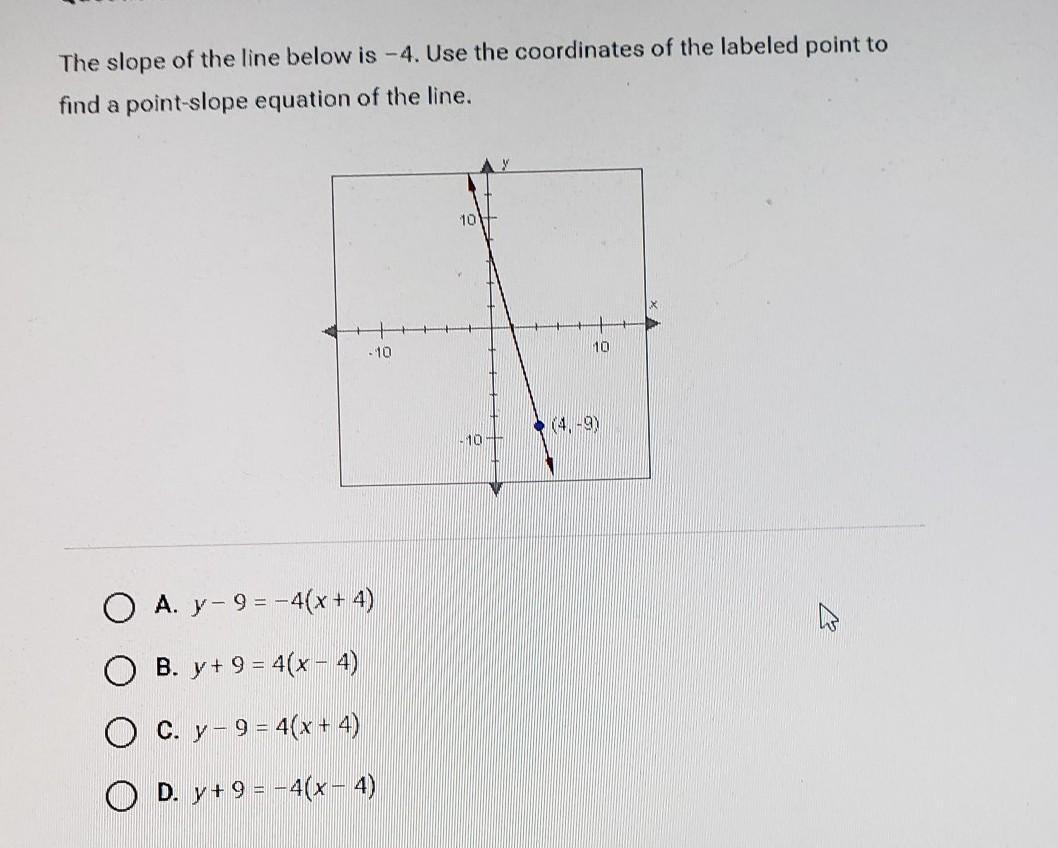
QUESTION 10 of 10 The slope of the line below is -4. Use the coordinates of the labeled point to find a point slope equation of the line.
Answers
Answer:
D:y+9=-4(x-4)
Step-by-step explanation:
The positive 9 comes from the top of the graph and its -4 because its on the lower half of the graph.
Related Questions
Solve 5x^2-2x-1=4x to the nearest tenth
Answers
The solutions to the nearest tenth are x = -0.1 and x = 1.3
Solving the equation to the nearest tenthFrom the question, we have the following parameters that can be used in our computation:
5x² - 2x - 1 = 4x
Evaluate the like terms
So, we have
5x² - 6x - 1 = 0
Next, we solve using a graph
The graph of 5x² - 6x - 1 = 0 is added as an attachment
From the attached graph, we can see that the curve intersects with the x-axis at x = -0.1 and x = 1.3
This means that the solutions are x = -0.1 and x = 1.3
Read more about quadratic functions at
https://brainly.com/question/1214333
#SPJ1

Answer:
The solutions to the equation 5x^2-2x-1=4x to the nearest tenth are x ≈ 1.3 or x ≈ -0.4.
Step-by-step explanation:
To solve the equation 5x^2-2x-1=4x to the nearest tenth, we can start by moving all the terms to one side of the equation.
5x^2-2x-1=4x
5x^2-6x-1=0
Next, we can use the quadratic formula to solve for x:
x = (-b ± sqrt(b^2 - 4ac)) / 2a
where a = 5, b = -6, and c = -1.
Plugging these values into the formula gives:
x = (-(-6) ± sqrt((-6)^2 - 4(5)(-1))) / 2(5)
x = (6 ± sqrt(56)) / 10
x ≈ 1.3 or x ≈ -0.4can you help me with this question i will give 40 points?

Answers
Which of the following shows the correct solution steps and solution to 2×+ 7 = -11?
Answers
Answer:
x = - 9
Step-by-step explanation:
2x + 7 = - 11 ( subtract 7 from both sides )
2x = - 18 ( divide both sides by 2 )
x = - 9
The answer is:
x = -9
Work/explanation:
The point of equations is to find the variable's value by isolating it step-by-step.
For this equation, the variable is x.
To isolate it, I will perform a few operations.
First, I will subtract 7 from each side:
\(\sf{2x+7=-11}\)
\(\sf{2x=-11-7}\)
\(\sf{2x=-18}\)
Divide each side by 2
\(\sf{x=-9}\)
Hence, x = -9.
\(\rule{350}{4}\)
Tommy made $55 for mowing 5 lawns. How much money would he make for mowing 8 lawns?
Answers
Find the total in the retirement account given the following conditions:
Monthly contributions = $225
Interest rate = 4.99%
Years invested = 38
Answers
To find the total in the retirement account after 38 years of investing with monthly contributions and an interest rate of 4.99%, we can use the compound interest formula.
The formula for the future value of an investment with regular monthly contributions is given by:
FV = P * [(1 + r)^n - 1] / r
Where:
FV is the future value or the total in the retirement account.
P is the monthly contribution amount.
r is the monthly interest rate (annual interest rate divided by 12).
n is the number of monthly contributions (years invested multiplied by 12).
Let's calculate the total:
P = $225
r = 4.99% / 100 / 12 = 0.0041583 (monthly interest rate)
n = 38 * 12 = 456 (number of monthly contributions)
FV = $225 * [(1 + 0.0041583)^456 - 1] / 0.0041583
Using a financial calculator or spreadsheet, we can evaluate this expression to find the future value or total in the retirement account.
The calculated total may vary depending on the compounding frequency and rounding used.
I need someone to solve b ASAP please help

Answers
b) The 99% confidence interval for the population proportion is given as follows: (0.57, 0.68).
What is a confidence interval of proportions?A confidence interval of proportions has the bounds given by the rule presented as follows:
\(\pi \pm z\sqrt{\frac{\pi(1-\pi)}{n}}\)
In which the variables used to calculated these bounds are listed as follows:
\(\pi\) is the sample proportion, which is also the estimate of the parameter.z is the critical value.n is the sample size.The confidence level is of 99%, hence the critical value z is the value of Z that has a p-value of \(\frac{1+0.99}{2} = 0.995\), so the critical value is z = 2.575.
The parameters for this problem are given as follows:
\(n = 520, \pi = \frac{325}{520} = 0.625\)
Then the lower bound of the interval is given as follows:
\(0.625 - 2.575\sqrt{\frac{0.625(0.375)}{520}} = 0.57\)
The upper bound of the interval is given as follows:
\(0.625 + 2.575\sqrt{\frac{0.625(0.375)}{520}} = 0.68\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
a. NewBank started its first day of operations with $155 million in capital. A total of $92 million in checkable deposits is received. The bank makes a $28 million commercial loan and lends another $23 million in mortgage loans. If required reserves are 5.4%, what does the bank balance sheet look like?
b. Suppose NewBank decides to invest $273 million in 30-day T-bills. The T-bills are currently trading at $4,981 (including commissions) for a $4,940 face value instrument. How many T-bills do they purchase? What does the balance sheet look like?
Answers
The balance sheet attached shows the Total Assets to be $55.968M and Total Liabilities and Capital to be $252M respectively.
Understanding Balance Sheet1. Assets:
a. Cash in Reserves:
The required reserves are 5.4% of checkable deposits.
Therefore, the required reserves amount to 5.4% of $92 million, which is:
(0.054 * $92 million) = $4.968 million.
This amount is considered a liability for the bank, but it is held as an asset in the form of cash reserves.
b. Loans: The bank made a $28 million commercial loan and a $23 million mortgage loan. Therefore, the total loans amount to:
total loan = $28 million + $23 million
= $51 million.
2. Liabilities:
a. Checkable Deposits:
The bank received $92 million in checkable deposits.
b. Required Reserves:
As mentioned above, the required reserves amount to $4.968 million.
3. Capital:
The bank started with $155 million in capital.
Based on the above information, the bank's balance sheet would look as attached.
Learn more about balance sheet here:
https://brainly.com/question/1113933
#SPJ1

Find the unknown coordinate so the line through the
points has the given slope

Answers
Answer:
#1 (0,-4)
#2 (5,0)
#3 (3,1)
Step-by-step explanation:
#1. (-3, 2) (0, y) slope = -2
slope = rise/run therefore slope = -2/1 or down 2 and over 1
so from -3 to 0 you are going over 3 units (or 3 times) Therefore to find y at x=0, you have to move three steps, or 3 times -2 = -6 so 2-6 = -4
so y intercept (b) = -4 0r (0,-4)
#2 (-7,-4) (x,0) slope (m) = 1/3 -7+12=5 x=5
#3 (4,-3) (x, 1) slope (m) = -4 (4/-1) Moving one unit in slope means
-3=4=1 for Y and 4-1=3 for X therefore the point is (3, 1)
There are 54 girls on the playground. There are 25 fewer boys than girls on the playground. How many kids are on the playground?
Answers
Answer:
83 kids total
Step-by-step explanation:
There are 54 girls on the playground. There are 25 fewer boys than girls on the playground. How many kids are on the playground?
girls = 54
boys = 54 - 25 = 29
54 + 29 = 83 kids total
kids that are on the playground are 83.
What is the sum?Merging objects and identifying them since one big bunch is done through addition. In arithmetic, addition is the technique of adding two or more integers together. The product can meet are the quantities that are included, and the outcome of the operation, or the final response, is referred to as the sum.
The total number of girls that are present is 54
The data given is that there are
25 fewer boys taht are4 present
The total number of boys will be
boys = 54 - 25 = 29
The number of kids that are present will be the total of boys and girls that are present.
Kids = boys + girls
54 + 29 = 83 kids total
The quantity of kids that are present in the playground is 83.
Learn more about sum, here:
https://brainly.com/question/537797
#SPJ2
A surveyor needs to determine the distance between two points that lie on opposite banks of a river. Two points, A and C, along one bank are 250 yards apart. The point B is on the opposite bank. Angle A is 64º and angle C is 51°. Find the distance between A and B to the nearest tenth of a yard. • Write your answer as a number only. • Round answer to one decimal place.
Answers
Answer:
does anyone know
Step-by-step explanation:
That is hard
fine -30 + ( -25) + 72
Answers
Find:
\(-30+(-25)+72\)step 1: open the bracket,
\(-30-25+72\text{ , note that (}+\times-=-)\)step 2: simplify step-wise
\(\begin{gathered} -30-25=-55 \\ -55+72=17 \end{gathered}\)The answer is 17
(5x + 3) (3x2 + 4x + 4)
Answers
Answer:
dggdhdhdhshsjshdhdhhshshshshdhdhsbsbsbd
but if youre factoring its (5x + 3) • 2 (2x + 5)
Simplify 15a6 bc4/ 35a2 c4

Answers
The simplified value of the expression given is 3a⁴b/ 7
Given the fraction :
15a⁶bc⁴/ 35a²c⁴divide the coefficients by 5
3a⁶bc⁴/ 7a²c⁴From division rule of indices, subtract the powers of values with Equivalent coefficients.
Hence,
coefficient of of a = 6-2 = 4coefficient of c = 4-4 = 0coefficient of b = bFinally we have :
3a⁴b/ 7Learn more on fractions : https://brainly.com/question/78672
#SPJ1
Please indicate which is the best answer to complete the figure below.

Answers
Answer:
Step-by-step explanation:
B because after having the star and the circle comes the square.
ILL GIVE BRAINLIEST IF ITS RIGHT
FREE BRAINLIEST
Jessie started a record collection with 8 records. Each week he added 3 records to his collection. Riley started her record collection with 23 records. Each week she gave away 2 records.
d) When will Jessie & Riley have the same number of records in their collection?
How many records will they each have at this time?
Answers
Answer:
when Riley starts selling her $h1t
Given the speeds of each runner below, determine who runs the fastest.
Debbie runs 10 feet per second.
Stephanie runs 131 feet in 10 seconds.
Jessica runs 1 mile in 440 seconds.
Ron runs 547 feet in 1 minute.
Debbie
Stephanie
Jessica
Ron
Answers
Answer:
Debbie runs 9 feet per second: 9 ft/s
Jessica runs 1 mile in 440 seconds: 414/50 ft/s = 207/25 ft/s = 8 7/25 ft/s
jesssica runs 131 feet in 10 seconds: since 1 mile = 5280 ft we have 1/470 mi/s = 5280/470 ft/s = 528/47 ft/s = 11 11/47 ft/s
ron runs 603 feet in 1 minute: 547 ft/min = 603/60 ft/s = 201/20 ft/s = 10 1/20 ft/s
Since:
11 11/47 > 10 1/20 > 9 > 8 7/25
Emily runs the fastest.
Hello, good night, can someone help me?

Answers
Answer:
b
Step-by-step explanation:
pls mark me as brainliest pls
HOW MANY GALLONS OF GASOLINE THAT IS 9% ETHANOL MUST BE ADDED TO 2,000 GALLONS OF GASOLINE WITH NO ETHANOL TO GET A MIXTURE THAT IS 7% ETHANOL.
Answers
The required 7,000 gallons of gasoline which are 9% ethanol must be added to 2,000 gallons of gasoline with no ethanol to get a mixture that is 7% ethanol.
What is the Ratio?The ratio can be defined as the proportion of the fraction of one quantity towards others. e.g.- water in milk.
Here,
To solve the problem, we can use the following formula:
(amount of ethanol in the final mixture) / (total amount of gasoline in the final mixture) = 7%
To find the amount of ethanol in the 2,000 gallons of gasoline with no ethanol:
ethanol in 2,000 gallons of gasoline with no ethanol = 0 × 2,000 = 0 gallons
Then, find the amount of ethanol in the final mixture:
ethanol in final mixture = (0.09x + 0 * 2,000) / (x + 2,000)
Notice that we use 0 gallons for the ethanol in the 2,000 gallons of gasoline with no ethanol, since it contains no ethanol.
Ethanol in the final mixture / total amount of gasoline in the final mixture = 7%
(0.09x + 0) / (x + 2,000) = 0.07
0.09x + 0 = 0.07(x + 2,000)
0.09x = 0.07x + 140
0.02x = 140
x = 7,000
Therefore, 7,000 gallons of gasoline which is 9% ethanol must be added to 2,000 gallons of gasoline with no ethanol to get a mixture that is 7% ethanol.
Learn more about ratios here:
brainly.com/question/13419413
#SPJ1
A survey was given to a random sample of the residents of a town to determine whether they support a new plan to raise taxes in order to increase education spending. The survey reported a confidence interval that between 22% and 32% of the residents supports the plan. What is the margin of error on the survey? Do not write ± ± on the margin of error.
Answers
Answer:
\(\Huge \bold{\boxed{\boxed{\text{5\%}}}}\)
Step-by-step explanation:
To calculate the margin of error for the survey, we need to use the formula:
\(\large \text{Margin of error} = \large \text{$\frac{\text{Range of values}}{2}$}\)
The range of values is the difference between the upper and lower bounds of the interval. In this case, the lower bound is 22% and the upper bound is 32%, so the range of values is:
\(\large \text{Range of values = 32\% - 22\% = 10\%}\)
Substituting this value into the formula, we get:
\(\large \text{Margin of error = $\frac{10\%}{2}$ = 5\%}\)
Therefore, the margin of error on the survey is 5%.
Which expression is equival 81 1/3?
Answers
Answer: 3^3 Square root 3
Step-by-step explanation:
Find x plss:))))))))

Answers
Answer:
180 - 90 = 90
half of 90 = 45
40 and 50??
Step-by-step explanation:
Help! I’ll mark brainlest :(
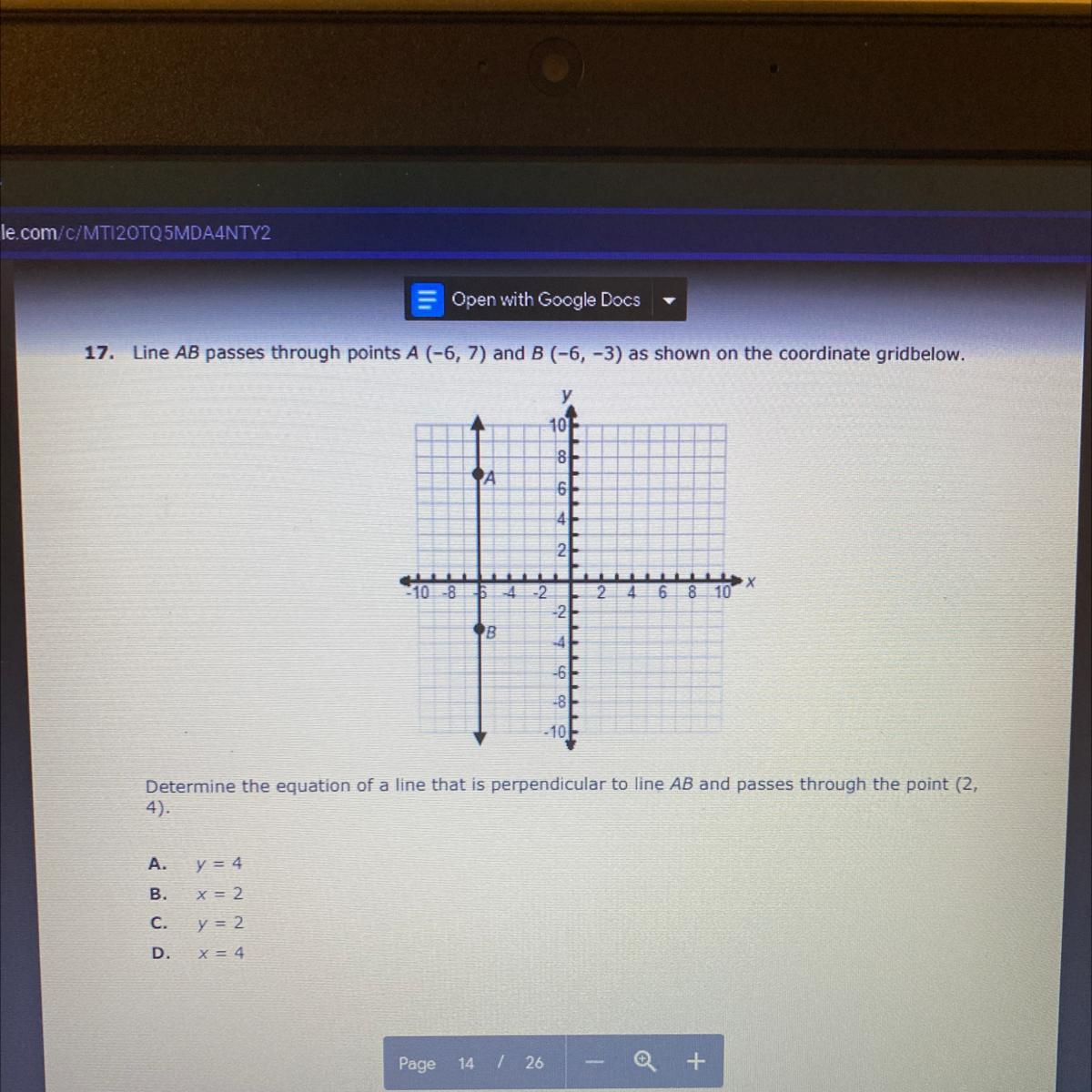
Answers
Answer:
A) y = 4
Step-by-step explanation:
Line AB is a vertical line, so a line perpendicular to it would have to be a horizontal line (perpendicular lines make an "x" shape with one another). Horizontal lines are written as y = ___ .
The perpendicular line also has to pass through the point (2,4). Points are written as (x, y). Therefore, the y-value in (2,4) is 4.
The perpendicular line has to be y=4 since it passes through both the Line AB and the given point.
¿De qué número 64 es el 80%?
Answers
Your parents allow you to borrow a car to get to your part-time job, but you have to pay for a tank of gas each month. Gasoline costs $2.76/gallon and the tank takes 15 gallons. You have 2 coworkers who are each willing to pay for a quarter of a tank each month to carpool with you to work. How much do you save each month?
$16.46
$20.70
$15.91
$18.55
Answers
What percentage of the total variation in test scores is not explained by the linear relationship between years of study and test scores?
Answers
Answer:
Check explanation section.
Step-by-step explanation:
So, we have the following parameters or information from the question above:
=> that the regression equation is Score = 31.55 + 10.90 Years.
So, the regression equation is in the form of mx + c.
Thus, the coefficient that is constant = 31.55 and the coefficient that shows or represents the years = 10.90.
=> Also, we have the value which is most important in this question that is the coefficient of Determination which is represented as R-sq and has the value of 83%.
The percentage of the total variation in test scores is NOT explained by the linear relationship between years of study and test scores = 100% - 83% = 17%.
For the percentage of the total variation in test scores is explained by the linear relationship between years of study and test scores = R- sq = 83%.
Use the definition to calculate the derivative of the following function. Then find the values of the derivative as specified.

Answers
Answer:
Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.
Step-by-step explanation:
Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11
\(p(\theta)=\sqrt{11\theta}\)
\(\hrulefill\)
The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.
\(f'(x) = \lim_{{h \to 0}} \dfrac{{f(x+h) - f(x)}}{{h}}\)\(\hrulefill\)
To apply the definition of derivatives to this problem, follow these step-by-step instructions:
Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).
\(p(\theta)=\sqrt{11\theta}\)
Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:
\(p'(\theta) = \lim_{{h \to 0}} \dfrac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h}\)
Step 3: Take the limit:
We need to rationalize the numerator. Rewriting using radical rules.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h} \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11\theta + 11h} - \sqrt{11\theta} }{h}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h}\)
Now multiply by the conjugate.
\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h} \cdot \dfrac{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} } \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{(\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} )(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )} \\\\\\\)
\(\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11h}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\)
Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.
\(p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta+(0)} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\)
\(\therefore \boxed{\boxed{p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta} }}}\)
Thus, we have found the derivative on the function using the definition.
It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.\(\hrulefill\)
Now evaluating the function at the given points.
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}; \ p'(1)=??, \ p'(11)=??, \ p'(\frac{3}{11} )=??\)
When θ=1:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(1)= \dfrac{\sqrt{11} }{2\sqrt{1}}\\\\\\\therefore \boxed{\boxed{p'(1)= \dfrac{\sqrt{11} }{2}}}\)
When θ=11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(11)= \dfrac{\sqrt{11} }{2\sqrt{11}}\\\\\\\therefore \boxed{\boxed{p'(11)= \dfrac{1}{2}}}\)
When θ=3/11:
\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(\frac{3}{11} )= \dfrac{\sqrt{11} }{2\sqrt{\frac{3}{11} }}\\\\\\\therefore \boxed{\boxed{p'(\frac{3}{11} )= \dfrac{11\sqrt{3} }{6}}}\)
Thus, all parts are solved.
Classify the function as linear or quadratic and identify the quadratic, linear, and constant terms. y=(3x+4)(-2x-3)
Answers
Answer:
\( y = -6x^2 -17 x -12\)
And since the higher exponent for the x term is 2 we can classify the equation as quadratic
Quadratic term: -6
Linear term: -17
Constant term: -12
Step-by-step explanation:
For this problem we have the following equation:
\( y = (3x+4)(-2x-3)\)
And we can distribute the terms and we got:
\( y = -6x^2 -9x -8x -12\)
And solving we got:
\( y = -6x^2 -17 x -12\)
And since the higher exponent for the x term is 2 we can classify the equation as quadratic
Quadratic term: -6
Linear term: -17
Constant term: -12
In the past year, Michael watched 14 movies that he thought were very good. He watched 40 movies over the whole year. Of the movies he watched, what percentage did he think were very good?
Answers
Answer:
35%
Step-by-step explanation:
14÷40= 0.35 (35%)
0.35 × 40= 14
The sum of 2/3, 7/8 and 1 2/5 is
Answers
Answer:
2/3=0.66
7/8=0.875
1 2/5= 1.4
Step-by-step explanation:
It's pretty simple if you have a calculator to divide 2/3 along with 7/8 and 1 2/5
Answer:
353/120 or 2 113/120
Step-by-step explanation:
i need help on these please

Answers
The cost of gas is proportional to the volume of gas because a constant rate of $3.15 to 1 gallon of gas.
How to calculate the constant rate of gas?From the given table;
The volume of the first gas Layla bought = 3 gallons.
The cost of the 3 gallons = 9.45
Therefore the cost of 1 gallon = ?
That is:
3 gallons = $9.45
1 gallon = X
Make X the subject of formula:
X = 9.45/3 = $3.15
Therefore, the cost of 11 gallons of gas would be = 11×3.15 = $34.65. This is because the cost of 1 gallon would be = $3.15.
Learn more about division here:
https://brainly.com/question/25289437
#SPJ1