Practice & Problem Solving
Identify the domain and range
{(2, 1), (4, 2), (6, 3), (8, 4), (10,5)}
Answers
Answer:
It has a constant order in the problem
X (Domain): 2 up every time Y goes up 1
Y (Range): 1 up every time X goes up 2
This is constant and will NOT be broken factor
Related Questions
The price of a 32'' LED Television is ₱15,500 less than twice of an OLD MODEL. If it cost ₱29,078.00 to buy the NEW 32'' LED Television, what is the price of the old model
NONSENCE = Report :(
Pwede rin po ba makita yung solution? Okay lang din po kahit hindi. Thank you in adavance din po:)
Answers
The price of the old model is ₱42,656.00. This answer is found by using the equation that the price of the old model is twice the price of the new model, minus the difference in price of ₱15,500.
What is equation?Equations can be written using symbols, numbers, and letters, and includes an equal sign (=) to show that two sides of the equation are equal in value.
The price of the old model can be calculated using the following equation:
Old Model Price = 2(New Model Price) - 15,500
Old Model Price = 2 (29,078) - 15,500
Old Model Price = 58,156 - 15,500
Old Model Price = ₱42,656.00
Therefore, the price of the old model is ₱42,656.00
This equation can be used in general when comparing the price of a new and old model of the same item. By subtracting the difference in price of the two models from twice the price of the new model, we can find the price of the old model.
For more questions related to price
https://brainly.com/question/1153322
#SPJ1
The perimeter of a rectangle is 66cm.
Its longest side has a length of 17cm.
State the length of the shortest side.
Answers
\({ \red{\boxed{ \tt{Step-by-step-explaination}}}}\)
Perimeter of a rectangle : \({ \purple{ \tt{2(l+b)}}}\)
length = \({ \red{ \tt{17cm}}}\)
breadth= \({ \red{ \tt{?}}}\)
now,
according to the rule.
perimeter = 2(l+b)
66 = 2(17+b)
66 = 34 + 2b
66 - 34 = 2b
32 = 2b
32/2 = b
16 cm = b
hence b = \({ \pink{ \sf{16cm}}}\)
if each of seven persons in a group shakes hands with each of the other six persons, then a total of forty-two handshakes occurs.
Answers
Answer:
false
Step-by-step explanation:
Call the persons 1 through 7.
1,2
1,3
1,4
1,5
1,6
1,7
2,3
2,4
2,5
2,6
2,7
3,4
3,5
3,6
3,7
4,5
4,6
4,7
5,6
5,7
6,7
There are 21 handshakes.
1 handshaking 2 is the same as 2 handshaking 1.
6 × 7/2 = 21
Answer: false
Which ordered pair is a solution to the following system of inequalities?
y < –x2 + x
y > x2 – 4
(0, –1)
(1, 1)
(2, –3)
(3, –6)
Answers
Answer: (0,-1)
Step-by-step explanation:
Let's start with the first inequality, \(y < -x^{2}+x\). To check which points satisfy this inequality, we can substitute the x- and y-coordinates and see if they satisfy the inequality.
A) \(-1 < -0^{2}+0 \longrightarrow -1 < 0 \longrightarrow \text{ True}\)B) \(1 < -1^{2}+1 \longrightarrow 1 < 0 \longrightarrow \text{ False}\)C) \(-3 < -2^{2}+2 \longrightarrow -3 < -2 \longrightarrow \text{ True}\)D) \(-6 < -3^{2}+3 \longrightarrow -6 < -6 \longrightarrow \text{ False}\)Once again, we can repeat this for the second inequality (but this time, we only need to check the points that satisfy the first inequality).
A) \(-1 > 0^{2}-4 \longrightarrow -1 > -4 \longrightarrow \text{ True}\)C) \(-3 > 2^{2}-4 \longrightarrow -3 > 0 \longrightarrow \text{ False}\)Therefore, the answer is (A) (0, -1).
How many solutions does -3=2x²-8x+8 have
Answers
The quadratic equation has two solutions, x1 = 3.44 and x2 = 0.56
What are Quadratic equations?Quadratic equations are the ones with degree 2. The standard form of a quadratic equation with variable x is ax2 + bx + c = 0, where a ≠ 0. These equations can be solved by splitting the factorisation, completing the square, or by quadratic formula method.
2x²-8x+8 = -3
2x²-8x+8+3 = 0
2x²-8x+11=0
Using the quadratic formula
x = (- b ± √(b² - 4ac)) / 2a
where a = 2
b = -8
c = 11
x = (-(-8) ± √(11² - 4(2)(11))) / 2(2)
x = (8 ± √(121 - 88)) / 4
x = (8 ± √(33))/4
x 1 = (8 + √(33))/4
x1 = (8 + √(33))/4
x1 = (8 + 5.75)/4
x1 = 13.75 / 4
x1 = 3.44
x2 = (8 - √(33))/4
x2 = (8 - 5.75)/4
x2 = 2.25/4
x2 = 0.56
Learn more about quadratic equations here: https://brainly.com/question/1214333
#SPJ1
⚠️please help done today⚠️
(03.01)
Which of the sums below can be expressed as 6(3 + 9)? (3 points)
O 18 + 54
O 18 + 9
O 9 + 15
O 6+54
Answers
Answer:
It would be the first answer choice, 18+54
Step-by-step explanation:
6(3+9
6x3=18
6x9=54
18+54 would be the equation.
Please pick me for brainliest
Answer:
a
Step-by-step explanation:
Which graph represents the function f(x) = 3x-2/X-2
Answers
Answer:
Step-by-step explanation:

Which of the sequences described below has -286 as its 50th term? A) An alternating geometric sequence where the 43rd term is 4 and the 45th term is 16 B) An arithmetic sequence where the 5th term is 7 and the 6th term is 10 C) - 8,2.-4... D) P - 326 - 324, 322
Answers
Option D cannot be evaluated to determine if -286 is its 50th term.
Based on the information provided, none of the given sequences can be identified as having -286 as its 50th term.
Let's evaluate each option to determine which sequence has -286 as its 50th term.
A) An alternating geometric sequence where the 43rd term is 4 and the 45th term is 16:
To determine the common ratio, we divide the 45th term by the 43rd term:
16 / 4 = 4.
Since this is an alternating geometric sequence, the terms alternate between positive and negative. However, since the common ratio is positive, this sequence will only have positive terms.
Therefore, option A cannot have -286 as its 50th term.
B) An arithmetic sequence where the 5th term is 7 and the 6th term is 10:
To determine the common difference, we subtract the 5th term from the 6th term:
10 - 7 = 3.
To find the 50th term, we use the formula for the nth term of an arithmetic sequence:
a_n = a_1 + (n - 1) * d,
where a_n is the nth term, a_1 is the first term, n is the term number, and d is the common difference.
a_50 = 7 + (50 - 1) * 3
a_50 = 7 + 49 * 3
a_50 = 7 + 147
a_50 = 154.
Since the 50th term of this arithmetic sequence is 154, option B cannot have -286 as its 50th term.
C) -8, 2, -4...
This sequence alternates between -8 and 2. To find the pattern, we can observe that each term is multiplied by -1 to get the next term. However, there is no indication of a geometric or arithmetic relationship between terms.
Therefore, option C cannot have -286 as its 50th term.
D) P, -326, -324, 322...
Since the sequence starts with P and there is no information given about its value, we cannot determine the specific value of the 50th term.
Therefore, Option D cannot be tested to see if -286 is the 50th term.
Learn more about sequences from the given link:
https://brainly.com/question/7882626
#SPJ11
Hallar la altura de una asta bandera, si un estudiante la observa desde un punto a, con un ángulo de 30° y entre el estudiante y la asta hay una distancia de 10m.
Answers
Answer:
The height of the flagpole is approximately 5.774 meters.
Step-by-step explanation:
Let's call the height of the flagpole h. We can use trigonometry to set up the following equation:
tan(30°) = h/10
Simplifying this equation, we get:
h = 10 tan(30°)
Using a calculator, we find that tan(30°) ≈ 0.5774, so:
h ≈ 5.774 meters
Therefore, the height of the flagpole is approximately 5.774 meters.
To know more about flagpole refer here
https://brainly.com/question/31296662#
#SPJ11
7. These values represent the expected number of paintings a person will produce over the next 10 days. 0, 0, 0, 1, 1, 1, 2, 2, 3, 5 a. What are the mean and standard deviation of the data? b. The artist is not pleased with these statistics. If the 5 is increased to a larger value, how does this impact the median, mean, and standard deviation?
Answers
The mean of a dataset is the average of the dataset.
The mean is 1.5The standard deviation is 1.58The median remains unchanged, the mean increases, and the standard deviation decreases when 5 is increased to a larger valueThe given parameters are:
\(\mathbf{x = 0, 0, 0, 1, 1, 1, 2, 2, 3, 5}\)
(a) Mean and Standard deviation
The mean of the dataset is calculated using:
\(\mathbf{\bar x = \frac{\sum x}{n}}\)
So, we have:
\(\mathbf{\bar x = \frac{0+ 0+ 0+ 1+ 1+ 1+ 2+ 2+ 3+ 5}{10}}\)
\(\mathbf{\bar x = \frac{15}{10}}\)
\(\mathbf{\bar x = 1.5}\)
Hence, the mean is 1.5
The standard deviation is calculated using:
\(\mathbf{\sigma_x = \sqrt{\frac{\sum(x - \bar x)^2}{n - 1}}}}\)
So, we have:
\(\mathbf{\sigma_x = \sqrt{\frac{(0 - 1.5)^2 + (0- 1.5)^2 + (0- 1.5)^2 + (1- 1.5)^2 + (1- 1.5)^2 + (1- 1.5)^2 + (2- 1.5)^2 + (2- 1.5)^2 + (3- 1.5)^2 + (5- 1.5)^2}{10 - 1}}}\)
\(\mathbf{\sigma_x = \sqrt{\frac{22.5}{9}}}\)
\(\mathbf{\sigma_x = \sqrt{2.5}}\)
\(\mathbf{\sigma_x = 1.58}\)
Hence, the standard deviation is 1.58
(b) When 5 is increased to a larger value
When 5 is increased:
The median remains unchangedThe mean increasesThe standard deviation decreasesRead more about median, mean, and standard deviation at:
https://brainly.com/question/12598273
Read each statement then select whether it is true or false.
True
False
O
§ * (5 x 8) is one-third of 5 * 8.
24 is two times as much as (12 + 12) 5
5 * 6+5 is five times as much as 6 +5.
is five times as much as 3 + 4.
O
5x

Answers
Answer:
1) true
2) false
3) false
4)True
In the adjoining figure, AE || BC. With the help of the given information find the value of x and y.
Hint: ZDAE = LABC ⇒x+19=y-11 ⇒x-y=-30 ...(1)
2x+y+y-11 +x+ 11 = 180⇒ 3x + 2y = 180...(ii).
Solve (i) and (ii)].
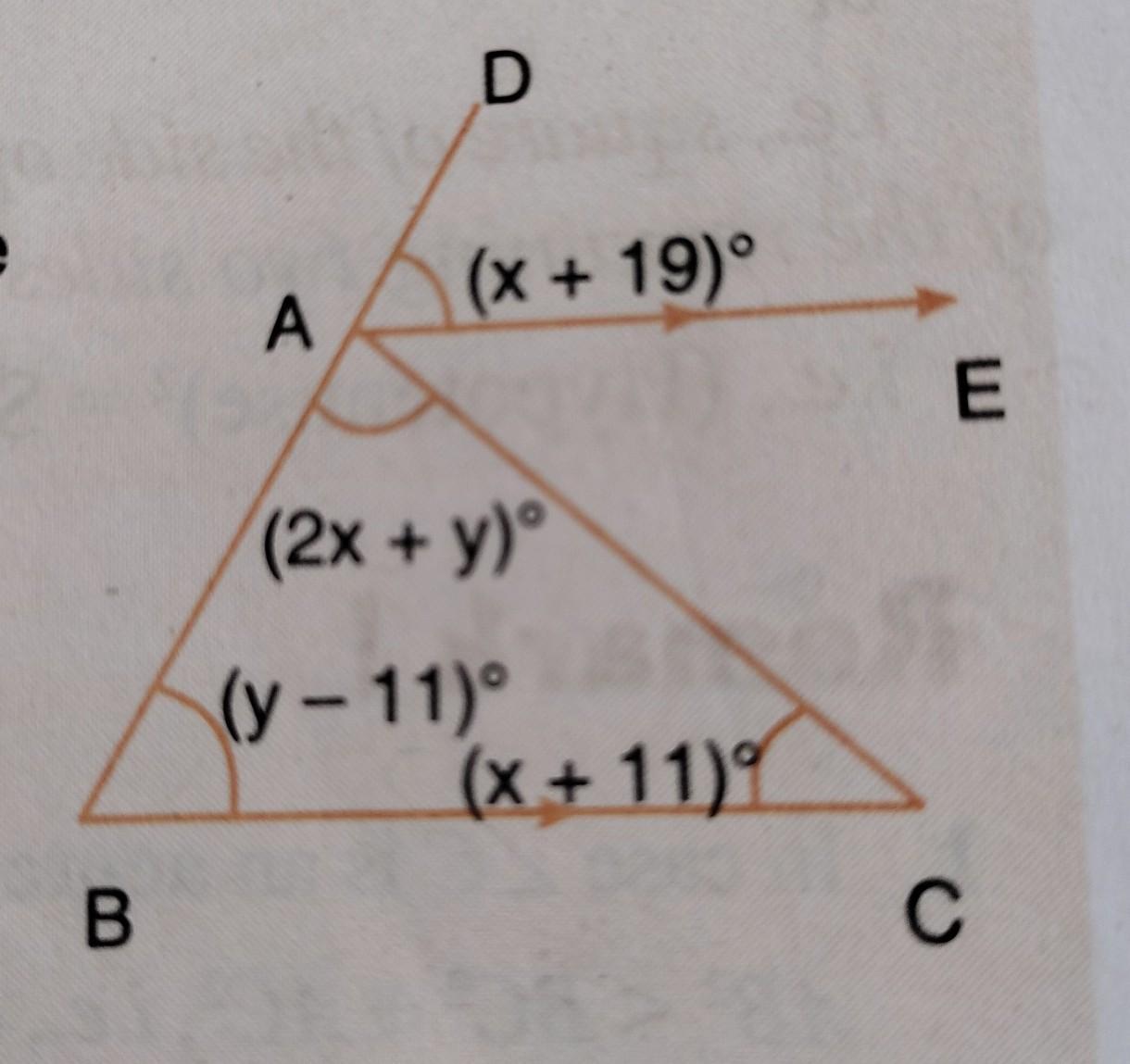
Answers
Answer: my name is pro this is the answer
Step-by-step explanation:
2+1= 3
Answer:
x = 24, y = 54
Explanation:
As AE and BC is parallel, angle DAE and ABC is equal.
Hence: x + 19 = y - 11
x + 19 + 11 = y
y = x + 30
A Triangle's Interior Angle's sum up to 180°
Hence: 2x + y + y - 11 + x + 11 = 180°
2x + x + 30 + x + 30 - 11 + x + 11 = 180
5x + 60 = 180
5x = 120
x = 24
Then find y: x + 30 = 24 + 30 = 54
A new bank customer with $2,500 wants to open a money market account. The bank is offering a simple interest rate of 1.3%. a. How much interest will the customer earn in 30 years? b. What will the account balance be after 30 years?
Answers
the answer is 975
Step-by-step explanation:
find out what 1.3% of 2500 then multiply it by 30
Write an equation in slope-intercept form for the line with slope
\( - \frac{3}{2} \)
and y-intercept 5.
Answers
The equation in slope-intercept form for the line is y = -3/2x + 5.
We have,
In slope-intercept form,
The equation of a line is written as y = mx + b, where m represents the slope of the line and b represents the y-intercept (the point where the line crosses the y-axis).
Given that the slope is -3/2 and the y-intercept is 5, we can substitute these values into the equation to obtain:
y = -3/2x + 5.
This equation tells us that for every increase of 1 unit in the x-coordinate, the y-coordinate decreases by 3/2 units.
The y-intercept of 5 indicates that the line passes through the point (0, 5).
Thus,
The equation in slope-intercept form for the line is y = -3/2x + 5.
Learn more about equation of a line here:
https://brainly.com/question/23087740
#SPJ1
What is the equation of the line that is parallel to the the line y-1 =4 (x+3) and passes through th point (4,32)
Answers
Calculation of slope: y-1=4(x+3) m= 4 and b=16
True or False: When conducting a survey of a group of people, you must interview every person in that population A Truc B False
Answers
The expression 35000(0.87)^t describes the value of a car years after it has been purchased. Interpret the coefficients of the expression in the context of this situation.
Answers
Answer: 35,000 · 0.87t
Step-by-step explanation: A coefficient is multiplying
An air compressor begins its cycle with 0.8 cu in of air at atmospheric pressure (14.7 psi or 0 psig) in its cylinder. The air leaving the cylinder has an absolute pressure of 42 psia. The temperature remains the same. What is the new volume of the air leaving the compressor
Answers
The new volume of the air leaving the compressor can be calculated using Boyle's Law, which states that for a fixed amount of gas at a constant temperature, the product of pressure and volume is constant.
According to Boyle's Law,\(P1V1 = P2V2\), where \(P1 and V1\) are the initial pressure and volume, and \(P2 and V2\) are the final pressure and volume, respectively. In this case, we are given the initial volume (V1 = 0.8 cu in) and the initial pressure (P1 = 14.7 psi), as well as the final pressure (P2 = 42 psia).
Using Boyle's Law, we can rearrange the formula to solve for \(V2:\)
\(V2 = (P1 * V1) / P2\)
Plugging in the values, we get:
V2 = (14.7 psi * 0.8 cu in) / 42 psia
Simplifying the equation, we find:
\(V2\) ≈ 0.280 cu in
Therefore, the new volume of the air leaving the compressor is approximately 0.280 cubic inches. It's important to note that this calculation assumes the temperature remains constant throughout the process.
Learn more about volume here:
https://brainly.com/question/28058531
#SPJ11
Can someone help please will mark brainlist

Answers
Answer:
A = 3, 4 B = 2, 6 C = -20, -24 D = 4, 8
Step-by-step explanation:
A is plus 1 B is plus 4 C is -4 and D is +4 :)
please I need help with this

Answers
Using the Sine-Law, value of c=18.5 units using ∠A= 47° , ∠C=74° and the side a = 14.1 units in the triangle.
What is Sine-Law?
The ratio of the sine of the angle to the length of the opposite side is known as the sine law. About their sides and angles, it applies to all three triangle sides. The triangle's sine rule The sine of angle A is divided by side A in the triangle ABC, which is equal to the sine of angle B divided by side B, which is equal to the sine of angle C divided by side C.
Sine Law:\(\frac{a}{SinA} =\frac{b}{SinB} =\frac{c}{SinC}\) or \(\frac{SinA}{a} =\frac{SinB}{b} =\frac{SInC}{c}\)
Given that: ∠A= 47° , ∠C=74° and the side a = 14.1
By taking, \(\frac{a}{SinA} =\frac{c}{SinC}\)
\(\frac{14.1}{Sin 47} =\frac{c}{Sin74}\)
\(\frac{14.1}{0.731}\) = \(\frac{c}{0.961}\)
c = \(\frac{14.1}{0.731}\) × 0.961
= 18.536 units
The value of c is 18.536, when rounded off to one decimal place is 18.5 units Option-C.
To know more about Sine-Law, visit:
https://brainly.com/question/27174058
#SPJ1
An electrician plans to install solar panels on a rectangular section of roof with an area of 180 m 2 180m 2 180, start text, m, end text, squared. this width of this section of roof is 7 1 5 m 7 5 1 ​ m7, start fraction, 1, divided by, 5, end fraction, start text, m, end text across. what is the length of this section of roof?
Answers
The length of the rectangular solar panel the electrician is installing is 25m
How to determine the length of the panelThe length of the panel is calculated from the Area of the panel which is given by the formula
Ares of rectangle = length * width
given units
area = 180 squared meters
width of the section = 7 1/5
From area = length * width
length = are / width
length = 180 / 7 1/5
length = 25 m
Learn more about rectangles at:
https://brainly.com/question/29322486
#SPJ1
Answer:
25m
Step-by-step explanation:
25m
PLEASE HELP
. The lengths of the sides of quadrilateral ABCD are equal. Prove that the perimeter of ABCD is equal to 4AB. GIVEN: AB BC BC &CD,CD = AD PROVE: Perimeter of ABCD = 4AB C I Statements Reasons 1. AB=BC ,BC =CD, CD SAD 2. AB = BC, BC= CD, CD = AD 3. AB = CD, AB= AD 3. 4. Perimeter of ABCD = AB + BC + CD + AD 5. 5. Substitution Property of Equality 6. 6. Simplify.

Answers
Answer:
Statements #5. P(ABCD) = AB + AB + AB + AB
Statements #6. P(ABCD) = 4•AB
Reasons #1. Give
Reasons #2. Def. Congruent Segments
Reasons #3. Transitive Prop. ≅
Reasons #4. Definition of Perimeter
How do i solve this math question?
d/2=4
I do not fully understand.
Answers
one card is to be selected at random from a deck of cards. find the probability that the card selected is: a) a 5 b) not a 5 c) a diamond or king d) a jack or queen e) a heart and a club f) a card greater than 6 and less than 9
Answers
The probability of outcome to be a 5 is 1/13. The probability of outcome not be 5 is 12/13. The probability of outcome to be a diamond or a king is 4/13. The probability of the outcomes to be a jack or a queen is 2/13. The probability of The outcome to be a heart and a club is 0 and the probability of the outcomes to be a card greater than 6 and less than 9 is 2/13.
A deck contains a total of 52 cards.
Total outcomes if the selected number of cards is one=52
Case A:
Each suit contain one 5 numbered card. There are four suits. Therefore, The required outcome would be 4.
Probability of an outcome is the ratio of desired outcomes to the total outcomes.
The probability of outcome to be 5, P(A):
P(A)=4/52
P(A)=1/13
Case B:
The total probability of outcomes=52/52=1
The probability of the outcome to be 5=1/13
Therefore, the probability of the outcome not to be 5, P(B):
P(B)=1-(1/13)
P(B)=12/13
Case C:
Each suit carries a king. Therefore, the probability of the outcome to be a king, P(M):
P(M)=4/52
P(M)=1/13
A suit carries 13 cards. Therefore, there will be 13 cards of diamonds.
The probability of the outcome to be a diamond, P(N):
P(N)=13/52
P(N)=1/4
The probability that the outcome is a king of diamonds, P(M\(\cap\)N):
P(M\(\cap\)N)=1/52
Hence, the probability that the outcome is a diamond or a king, P(M\(\cup\)N):
P(M\(\cup\)N)=P(M)+P(N)-P(M\(\cap\)N)
P(M\(\cup\)N)=(1/13)+(1/4)-(1/52)
P(M\(\cup\)N)=16/52
P(M\(\cup\)N)=4/13
Case D:
Each suit carries a Jack. Therefore, the probability of the outcome to be a jack, P(P):
P(P)=4/52
P(P)=1/13
Each suit carries a Queen. Therefore, the probability of the outcome to be a Queen, P(Q):
P(Q)=4/52
P(Q)=1/13
The probability that the outcome is a jack and a queen, P(P\(\cap\)Q):
P(P\(\cap\)Q)=0/52
P(P\(\cap\)Q)=0
Hence, the probability that the outcome is a jack or a queen, P(P\(\cup\)Q):
P(P\(\cup\)Q)=P(P)+P(Q)-P(P\(\cap\)Q)
P(P\(\cup\)Q)=(1/13)+(1/13)-0
P(P\(\cup\)Q)=2/13
Case E:
A card is never a heart and a club. Therefore, the probability of a card to be a heart and a club is 0.
Case F:
The numbers greater than 6 and less than 9 are the numbers between 6 and 9. The numbers between 6 and 9 are 7 and 8.
Each suit carries one 7 numbered card and one 8 numbered card. There is a total of 4 suits.
Therefore the desirable outcomes=8
The probability of the outcome required=8/52
=2/13
Learn more about probability here at:
https://brainly.com/question/28808092
#SPJ4
a. An electronic device consists of two components, A and B. The probability that component A will fail within the guarantee period is 0.2. There is also a 15 % chance that the component B will fail within the guarantee period. Assume the components operate entirely independently of each other. What is the probability that component A will fail within the guarantee period given that component B has failed already within the guarantee period? b. A batch of 1500 lemonade bottles has average contents of 753 ml and the standard deviation of the contents is 1.8 ml. If the volumes of the contents are normally distributed, find the number of bottles likely to contain less than 750 ml
Answers
a. The probability that component A will fail within the guarantee period given that component B has failed already within the guarantee period is 0.2 or 20%.
b. It is likely that around 71 bottles out of the batch of 1500 will contain less than 750 ml.
a. To find the probability that component A will fail within the guarantee period given that component B has already failed, we can use conditional probability.
The probability of component A failing within the guarantee period is 0.2, and the probability of component B failing within the guarantee period is 0.15. Since the components operate independently, we can multiply these probabilities to find the joint probability of both components failing within the guarantee period: P(A and B) = P(A) * P(B) = 0.2 * 0.15 = 0.03.
Now, to find the conditional probability of component A failing given that component B has failed, we use the formula for conditional probability: P(A|B) = P(A and B) / P(B).
Substituting the values we have: P(A|B) = 0.03 / 0.15 = 0.2.
Therefore, the probability that component A will fail within the guarantee period given that component B has already failed within the guarantee period is 0.2 or 20%.
b. To find the number of bottles likely to contain less than 750 ml, we need to convert the given information into a standard normal distribution.
The average volume of the contents is 753 ml, and the standard deviation is 1.8 ml. We can calculate the z-score for 750 ml using the formula: z = (x - μ) / σ, where x is the value, μ is the mean, and σ is the standard deviation.
Calculating the z-score: z = (750 - 753) / 1.8 ≈ -1.667.
Using a standard normal distribution table or calculator, we can find the probability corresponding to a z-score of -1.667, which is the probability of a bottle containing less than 750 ml.
Looking up the z-score in the standard normal distribution table, we find that the probability is approximately 0.0475.
To find the number of bottles likely to contain less than 750 ml, we multiply the probability by the total number of bottles: 0.0475 * 1500 = 71.25.
Therefore, it is likely that around 71 bottles out of the batch of 1500 will contain less than 750 ml.
To learn more about probability refer here:
https://brainly.com/question/31828911
#SPJ11
Finding Missing Angles and Sides and Round to the nearest tenth.
(FOR ALL PLEASE)




Answers
The right triangle, like the other triangles, has three sides, three vertices, and three angles. The difference between the other triangles and the right triangle is that the right triangle has a 90 angle.
To find missing angles and sides and round to the nearest tenth, you can use different methods depending on the given information and the type of triangle or shape involved.
Some common methods include:
Trigonometric ratios (sine, cosine, tangent) for right triangles.
Angle sum property or exterior angle property for triangles.
Pythagorean theorem for right triangles.
Law of cosines and law of sines for non-right triangles.
To help find the missing angles and sides of a triangle, you need certain information about the triangle, such as known angle and side measurements, or information about the properties of the triangle.
Without this information, no concrete calculations can be made.
Provide the necessary information or describe the problem in more detail and we will help you find the missing corners and sides of the triangle and round it to tenths.
Remember to always check if any additional information is given, such as side lengths or angles ' 7 and to apply the appropriate formula or property to find the missing value.
Round your answer to the nearest tenth as specified.
For more related questions on right triangle:
https://brainly.com/question/2773823
#SPJ8
find the minimum sample size needed to be 95% confident that the sample variance is within 5% of the population variance.
Answers
The minimum sample size needed for 95% confidence that the sample variance is within 5% of the population variance is given by n = (1.96² * σ²) / (0.05²).
Determine how to find the minimum sample size?The minimum sample size needed to be 95% confident that the sample variance is within 5% of the population variance can be calculated using the formula:
n = (Z² * σ²) / (E²)
where:
n is the minimum sample size,
Z is the z-score corresponding to the desired confidence level (in this case, 95% confidence corresponds to a z-score of approximately 1.96),
σ² is the population variance, and
E is the maximum allowable difference between the sample variance and the population variance (expressed as a proportion of the population variance).
The formula ensures that the desired confidence level is achieved while limiting the difference between the sample and population variances within the specified threshold.
In summary, to determine the minimum sample size needed to be 95% confident that the sample variance is within 5% of the population variance, you can use the formula n = (1.96² * σ²) / (0.05²), where σ² represents the population variance.
To know more about sample variance, refer here:
https://brainly.com/question/14988220#
#SPJ4
Interpret line plots with fraction addition and subtraction
The weights of 11 different babies are recorded on the line plot below. Each weight was rounded to the nearest
1
pound.
|||||
|||||
6 6
7
7층
8
8
9
9
What is the difference, in weight, between the two heaviest babies?
pounds
Your answer should be
a proper fraction, like 1/2 or 6/10
100
8
P100
10
Answers
To interpret this line plot with fraction addition and subtraction, we need to understand how to read the plot and how to perform the necessary calculations with fractions.
Looking at the line plot above, we can see that each horizontal line represents one pound, and each vertical line represents one baby's weight. The numbers on the vertical axis show the weights of the babies in pounds. For example, there are two babies that weigh 6 pounds, three babies that weigh 7 pounds, two babies that weigh 8 pounds, and so on. To find the difference in weight between the two heaviest babies, we need to first determine which babies are the heaviest. From the line plot, we can see that the two heaviest babies are the ones at the top of the plot, which both weigh 9 pounds. Converting the weight of the heaviest baby to a fraction with a denominator of 72 gives us 9/1 x 72/72 = 648/72. Converting the weight of the second heaviest baby to a fraction with a denominator of 72 gives us 8/1 x 72/72 = 576/72. Now that both weights are expressed as fractions with a common denominator, we can subtract them to find the difference: 648/72 - 576/72 = 72/72 = 1
Therefore, the difference in weight between the two heaviest babies is 1 pound, or 1/72 of a hundredweight (since there are 100 pounds in a hundredweight). The answer we were asked to provide is a proper fraction, so we can express this as 1/72. In summary, to interpret a line plot with fraction addition and subtraction, we need to understand how to read the plot to determine the weights of the babies, how to perform the necessary calculations with fractions, and how to express our answer as a proper fraction if required.
To know more about subtraction visit:-
https://brainly.com/question/1927340
#SPJ11
you are ordering shirts for a club at your school. the function f(x)=8x+12 represents the cost of ordered x shirts how much would it cost to buy 32 shirts
Answers
The cost of ordering shirts for a club is 268 units.
Define Function.
A function, according to a technical definition, is a relationship between a set of inputs and a set of possible outputs, where each input is connected to precisely one output.
This means that a function f will map an object x exactly to one object f(x) in the set of possible outputs if the object x is in the set of inputs (called the codomain).
The statement that f is a function from X to Y using the function notation f: X→Y
The function that represents the cost of the shirts(x) is f(x) = 8x+12
Now, for x = 32
f(x) = 8x+12
f(32) = 8(32) + 12
= 256 +12
f(32) = 268 units
.
To know more about Function visit:
brainly.com/question/12431044
#SPJ1
1 - -8= i am having trouble answering it
Answers
Answer:
Step-by-step explanation:
2 subtraction symbols equals a plus
so the answer is 9