Answers
Related Questions
Will give brainliest
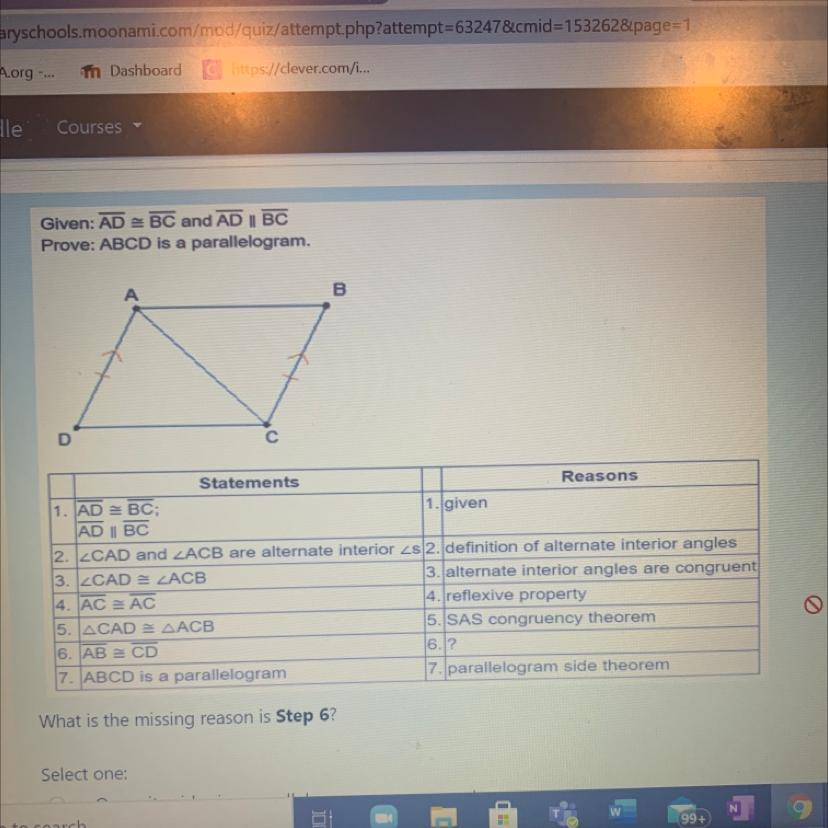
What is the missing reason in step six?
A. Opposite sides in a parallelogram are congruent
B. SSS
C. CPCTC
D. Definition of a parallelogram
Answers
CPCTC is the missing reason in step six.
CPCTC states that corresponding part of the congruent triangles are congruent.
Here, Given: ABCD is a quadrilateral,
In which AD ≅ BC and AD║BC
Prove : ABCD is a parallelogram.
Statement Reason
1. AD ≅ BC; AD║BC 1. Given
2.∠CAD and ∠ACD are alternative angles 2. Definition of alternative angles
3. ∠CAD ≅∠ACB 3. alternative angles are congruent
4. AC ≅ AC 4. Reflexive property
5.△CAB ≅ △ACB 5. SAS congruence postulate
6. .AB ≅ CD 6. CPCTC
7. ABCD is a parallelogram 7. Parallelogram side theorem
Therefore, CPCTC is six step.
Learn more about parallelogram here:
https://brainly.com/question/26768239
#SPJ2
A password is 4 characters long and must consist of 3 letters and one number. if letters cannot be repeated and the password must end with a number, how many possibilities are there? a. 175,760 b. 158,184 c. 156,000 d. 140,400 please select the best answer from the choices provided a b c d
Answers
The possibility of selecting a 4 characters long password consisting of 3 letters and one number if letters cannot be repeated and the password must end with a number is 156000
What is an equation?An equation is an expression that shows the relationship between two or more number and variables.
The possibility of selecting the password = 26 * 25 * 24 * 10 = 156000
The possibility of selecting a 4 characters long password consisting of 3 letters and one number if letters cannot be repeated and the password must end with a number is 156000
Find out more on equation at: https://brainly.com/question/2972832
#SPJ4
3,532.5 = (3.14)(r^2)(x/3)
Answers
To solve the equation 3,532.5 = (3.14)(r^2)(x/3) for the variable r, we can follow these steps:
Multiply both sides of the equation by 3/3 to eliminate the fraction:
3,532.5 * 3/3 = (3.14)(r^2)(x/3) * 3/3
This simplifies to:
10,597.5 = (3.14)(r^2)(x)
Divide both sides of the equation by (3.14)(x) to isolate the variable r:
10,597.5 / (3.14)(x) = (r^2)
Take the square root of both sides of the equation to solve for r:
r = sqrt(10,597.5 / (3.14)(x))
Therefore, the solution to the equation 3,532.5 = (3.14)(r^2)(x/3) for the variable r is:
r = sqrt(10,597.5 / (3.14)(x))
What is the area, measured in square centimeters, of the triangle below? Do
not include units in your answer.
Answer here

Answers
Answer:
The area of this triangle is (1/2)(9)(8) = 36.
NO LINKS!!! URGENT HELP PLEASE!!!
Solve ΔABC using the Law of Sines
1. A = 29°, C = 63°, c = 24
2. A = 72°, B= 35°, c = 21
Answers
Answer:
1) B = 88°, a = 13.1, b = 26.9
2) C = 73°, a = 20.9, b = 12.6
Step-by-step explanation:
To solve for the remaining sides and angles of the triangle, given two sides and an adjacent angle, use the Law of Sines formula:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Question 1Given values:
A = 29°C = 63°c = 24As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies B=180^{\circ}-A-C\)
\(\implies B=180^{\circ}-29^{\circ}-63^{\circ}\)
\(\implies B=88^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies a=\dfrac{24\sin 29^{\circ}}{\sin 63^{\circ}}\)
\(\implies a=13.0876493...\)
\(\implies a=13.1\)
Solve for b:
\(\implies \dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies b=\dfrac{24\sin 88^{\circ}}{\sin 63^{\circ}}\)
\(\implies b=26.9194211...\)
\(\implies b=26.9\)
\(\hrulefill\)
Question 2Given values:
A = 72°B = 35°c = 21As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies C=180^{\circ}-A-B\)
\(\implies C=180^{\circ}-72^{\circ}-35^{\circ}\)
\(\implies C=73^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies a=\dfrac{21\sin 72^{\circ}}{\sin 73^{\circ}}\)
\(\implies a=20.8847511...\)
\(\implies a=20.9\)
Solve for b:
\(\implies \dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies b=\dfrac{21\sin 35^{\circ}}{\sin 73^{\circ}}\)
\(\implies b=12.5954671...\)
\(\implies b=12.6\)
What is the surface area of the sphere below?
5
2.5
A. 1257 units2
B. 1007 units2
C. 12573 units2
O
D. cannot be determined

Answers
Here's the solution :
In a sphere,
\( \boxed{ \mathsf{surface \: \: area = 4\pi {r}^{2} }}\)
now, let's solve :
\(s = 4 \times \pi \times 5 \times 5\)\(s = 100\pi\)hence, correct answer is B. 100π unit²
The surface area of the sphere is 100 π unit².
The correct option is B.
What is Surface area?The area is the area occupied by a two-dimensional flat surface. It has a square unit of measurement. The surface area of a three-dimensional object is the space taken up by its outer surface. Square units are used to measure it as well.
We have,
Radius of Sphere= 5 unit
Now, the formula for Surface area of Sphere is
= 4πr²
= 4 (3.14) (5)(5)
= 4 x 3.14 x 25
= 314
= 10 π unit²
Thus, the Surface area is 10 π unit².
Learn more about Surface area here:
https://brainly.com/question/29101132
#SPJ7
Help help help hehehheheheh

Answers
Answer:
Step-by-step explanation:
your supposed to learn things in class pay attetion
Use the function f(x) to answer the questions:
f(x) = 2x2 − 5x + 3
Part A: What are the x-intercepts of the graph of f(x)? Show your work.
Part B: Is the vertex of the graph of f(x) going to be a maximum or a minimum? What are the coordinates of the vertex? Justify your answers and show your work.
Part C: What are the steps you would use to graph f(x)? Justify that you can use the answers obtained in Part A and Part B to draw the graph.
Answers
The x-intercepts of the graph of f(x) are x = 3/2 and x = 1,the Vertex of the graph of f(x) is (5/4, 3/8), and it is a minimum point, The vertex is at (5/4, 3/8). This is the minimum point of the graph.
Part A: To find the x-intercepts of the graph of f(x), we set f(x) equal to zero and solve for x.
2x^2 - 5x + 3 = 0
To factor this quadratic equation, we look for two numbers that multiply to give 3 (the coefficient of the constant term) and add up to -5 (the coefficient of the linear term). These numbers are -3 and -1.
2x^2 - 3x - 2x + 3 = 0
x(2x - 3) - 1(2x - 3) = 0
(2x - 3)(x - 1) = 0
Setting each factor equal to zero, we get:
2x - 3 = 0 --> x = 3/2
x - 1 = 0 --> x = 1
Therefore, the x-intercepts of the graph of f(x) are x = 3/2 and x = 1.
Part B: To determine whether the vertex of the graph of f(x) is a maximum or a minimum, we look at the coefficient of the x^2 term, which is positive (2 in this case). A positive coefficient indicates that the parabola opens upwards, so the vertex will be a minimum.
To find the coordinates of the vertex, we can use the formula x = -b/2a. In the equation f(x) = 2x^2 - 5x + 3, the coefficient of the x term is -5, and the coefficient of the x^2 term is 2.
x = -(-5) / (2*2) = 5/4
Substituting this value of x back into the equation, we can find the y-coordinate:
f(5/4) = 2(5/4)^2 - 5(5/4) + 3 = 25/8 - 25/4 + 3 = 3/8
Therefore, the vertex of the graph of f(x) is (5/4, 3/8), and it is a minimum point.
Part C: To graph f(x), we can use the information obtained in Part A and Part B.
- The x-intercepts are x = 3/2 and x = 1. These are the points where the graph intersects the x-axis.
- The vertex is at (5/4, 3/8). This is the minimum point of the graph.
We can plot these points on a coordinate plane and draw a smooth curve passing through the x-intercepts and the vertex. Since the coefficient of the x^2 term is positive, the parabola opens upwards, and the graph will be concave up.
Additionally, we can consider the symmetry of the graph. Since the coefficient of the linear term is -5, the line of symmetry is given by x = -(-5) / (2*2) = 5/4, which is the x-coordinate of the vertex. The graph will be symmetric with respect to this line.
By connecting the plotted points and sketching the curve smoothly, we can accurately graph the function f(x).
For more such questions on Vertex .
https://brainly.com/question/28747454
#SPJ8
A grocery store sells a bag of 5 lemons for $3.00. What is the unit cost of each lemon in the bag?
Answers
Answer:
the unit cost of each lemon is $0.60
Step-by-step explanation:
divide 3.00 by 5 to get 0.6
Suppose ΔDEF is the image of a translation of ΔABC. If D is at (−6, −2), what translation rule maps ΔABC to ΔDEF? * Captionless Image T⟨9, 2⟩(ΔABC) = ΔDEF T⟨9, –2⟩(ΔABC) = ΔDEF T⟨–9, –2⟩(ΔABC) = ΔDEF T⟨−9, 2⟩(ΔABC) = ΔDEF
Answers
Answer:
T⟨–9, –2⟩(ΔABC) = ΔDEF
Step-by-step explanation:
The question ask what the translation from A is to D(-6,-2). When you solve, you will get (-9,-2) as your answer.
Which expression is equivalent to 9 + 4y + 5 + 22 + 8?
Answers
Answer: The answer is 11x+4y+13
What else would need to be congruent to show that ABC DEF by SAS? E AA. А B OA. BC = EF B. CF OC. ZA ZD D. AC = OF F Given: AC = DF CE F

Answers
The two triangles exist congruent if they contain two congruent corresponding sides and their contained angles exist congruent.
Let \($&\overline{A B} \cong \overline{D E} \\\) and \($&\overline{A C} \cong \overline{D F}\)
Angle between \($\overline{A B}$\) and \($\overline{A C}$\) exists \($\angle A$\).
Angle between \($\overline{D E}$\) and \($\overline{D F}$\) exists \($\angle D$\).
Therefore, \($\triangle A B C \cong \triangle D E F$\) by SAS, if \($\angle A \cong \angle D$$\).
What is SAS congruence property?Given:
\($&\overline{A B} \cong \overline{D E} \\\) and
\($&\overline{A C} \cong \overline{D F}\)
According to the SAS congruence property, two triangles exist congruent if they contain two congruent corresponding sides and their contained angles exist congruent.
Let \($&\overline{A B} \cong \overline{D E} \\\) and \($&\overline{A C} \cong \overline{D F}\)
Angle between \($\overline{A B}$\) and \($\overline{A C}$\) exists \($\angle A$\).
Angle between \($\overline{D E}$\) and \($\overline{D F}$\) exists \($\angle D$\).
Therefore, \($\triangle A B C \cong \triangle D E F$\) by SAS, if \($\angle A \cong \angle D$$\).
To learn more about SAS congruence property refer to:
https://brainly.com/question/19807547
#SPJ9
simplify-18z3 +(-15z3)
Answers
Answer:
-18z3+(-15z3)
-18z3-15z3
-33z6
10/15 as a % to 2 decimal places
Answers
Answer:
0.67
Step-by-step explanation:
all you need to do is divide 10 by 15
the cost of a family membership at the health club is $58 per month plus a one-time $129 startup fee if a family spend $651 how many months in their membership
Answers
Answer:
Step-by-step explanation:
58 x 12 = 696 696 + 129 = $825 for a year
they are 9 months in
How many ¼ pound bags of nuts can be made from a 2 1/2 pound bag of nuts?
Answers
There are 16 ounces in a pound.
A 1/4 pound bag of nuts is equal to 1/4 * 16 = <<1/416=4>>4 ounces.
Therefore, you can make 40/4 = <<40/4=10>>10 1/4 pound bags of nuts from a 2 1/2 pound bag of nuts.
Answer:
9 bags
Step-by-step explanation:
2 1/4 ÷ 1/4
9/4 ÷ 1/4
9/4 x 4/1 = 9
Three poultry farms B1, B2, and B3 supply chicken eggs to the same local market. The market performs some quality testing on the supplied eggs. It has been observed that 80% of eggs supplied by B1 are acceptable. 90% eggs of Farm B2 are acceptable and only 60% eggs of farm B3 is acceptable. Each week, farm B1 supplies 3000 eggs, B2 supplies 4000 eggs and B3 supplies 3000 eggs. All of the eggs are put together at random in one bin and packed for sale by the local market. a) What is the probability that an egg come from Farm B1 or B2? b) What is the probability that the market received an egg that is acceptable?
Answers
Answer:
a. 0.58
b. 0.78
Step-by-step explanation:
a. The probability of egg come from B1 or B2
P(B1) = 3000/10000 = 0.3
P(B2) = 4000/10000 = 0.4
P(P1 ∪ B2) = 0.3 + 0.4 -(0.3)(0.4)
P(P1 ∪ B2) = 0.7 - 0.12
P(P1 ∪ B2) = 0.58
b. The probability that the market received an egg that is acceptable
P(received an egg that is acceptable) = P(B1 acceptable) + P(B2 acceptable) + P(B3 acceptable)
P(received an egg that is acceptable) = 0.80*3000 + 0.90*4000 + 0.60*3000 / 10000
P(received an egg that is acceptable) = 2400 + 3600 + 1800 / 10000
P(received an egg that is acceptable) = 7800 / 10000
P(received an egg that is acceptable) = 0.78
Ephemeral services corporation (esco) knows that nine other companies besides esco are bidding for a $900,000 government contract. each company has an equal chance of being awarded the contract. if esco has already spent $100,000 in developing its bidding proposal, what is its expected net profit?
a. $10,000
b. $0
c. $100,000
d. $90,000
Answers
Answer:
c. $100,000
Step-by-step explanation:
Calculation of the expected net profit of Ephemeral services corporation
Since we are been told that 9 other companies besides esco are as well bidding for the $900,000 government contract, it means we have to find the expected net profit by dividing 1 by 9×$900,000 .Thus ESCO can only expect to cover its sunk cost.
Hence ,
E(X) = (1/9) × $900,000
E(X)=0.111111111×$900,000
E(X)= $100,000
Therefore the expected net profit would be $100,000
PLEASE HELP options are in the picture
A game involves rolling a fair six-sided die. If the number obtained on the die is a multiple of three, the player wins an amount equal to the number on the die times $20. If the number is not a multiple of three, the player gets nothing.
How will you model the simulation for the roll of a die?

Answers
Answer: C. Use the numbers 1-3 to represent all the outcomes.
Step-by-step explanation: I got this question correct on Edmentum.

Some boys and girls are waiting for school buses. 25 girls get on the first bus. The ratio of boys to girls at the stop is now 3:2. 15 boys get on the second bus. There are now the same number of boys and girls at the bus stop. How many students were originally at the bus stop?
Answers
Answer:
100
Step-by-step explanation:
Forming algebraic equations and solving:
Let the number of boys originally at the stop = 'x'
Let the number of girls originally at the stop = 'y'
25 girls get on the first bus.
⇒ The number of girls now at the stop = y -25
Ratio of boys to girls:
\(\sf \dfrac{x}{y -25}= \dfrac{3}{2}\\\\Cross \ multiply,\\\\2x = 3*(y- 25)\\\\2x = 3y - 3*25\\\\2x = 3y - 75 ------\)(I)
15 boys get on the second bus.
Now, the number of boys at the stop = x - 15
Number of girls at the stop = y - 25
Ratio of boys to girls,
\(\sf \dfrac{x - 15}{y -25} = \dfrac{1}{1}\\\\Cross \ multiply, \\\\x - 15 = y -25\\\\\)
x = y -25 + 15
x = y - 10
Plugin x = y - 10 in equation (I)
2*(y-10) = 3y -75
2y - 20 = 3y -75
-20 = 3y - 75 - 2y
-20 = y -75
-20 +75 = y
\(\sf \boxed{\bf y = 55}\)
Plugin y = 55 in equation (I)
x = 55 -10
\(\sf \boxed{\bf x = 45}\)
Number of students originally at the stop = x + y
= 55 + 45
= 100
She has a budget of $500. Which two items together cost 34% of her budget.
Answers
The two items that together cost 34% of her budget have a summed cost of $170
Which two items together cost 34% of her budget.From the question, we have the following parameters that can be used in our computation:
She has a budget of $500.
To calculate which two items together cost 34% of her budget, we use
Amount = 34% * Budget
substitute the known values in the above equation, so, we have the following representation
Amount = 34% * 500
Evaluate
Amount = 170
Hence, the two items would have a summed cost of $170
Read mroe about percentage at
https://brainly.com/question/843074
#SPJ1
Please solve this
∫ (log(1 + x ^ 2))/((x + 1) ^ 2) dx
Answers
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
We have,
To solve the integral ∫ (log(1 + x²) / (x + 1)²) dx, we can use the method of substitution.
Let's substitute u = x + 1, which implies du = dx. Making this substitution, the integral becomes:
∫ (log(1 + (u-1)²) / u²) du.
Expanding the numerator, we have:
∫ (log(1 + u² - 2u + 1) / u²) du
= ∫ (log(u² - 2u + 2) / u²) du.
Now, let's split the logarithm using the properties of logarithms:
∫ (log(u² - 2u + 2) - log(u²)) / u² du
= ∫ (log(u² - 2u + 2) / u²) du - ∫ (log(u²) / u²) du.
We can simplify the second integral:
∫ (log(u²) / u²) du = ∫ (2 log(u) / u²) du.
Using the power rule for integration, we can integrate both terms:
∫ (log(u² - 2u + 2) / u²) du = log(u² - 2u + 2) / u - 2 ∫ (log(u) / u³) du.
Now, let's focus on the second integral:
∫ (log(u) / u³) du.
This integral does not have a simple closed-form solution in terms of elementary functions.
It can be expressed in terms of a special function called the logarithmic integral, denoted as Li(x).
Therefore,
The final result of the integral is:
∫ (log(1 + x²) / (x + 1)²) dx = log(x + 1) - 2 (log(x + 1) / x) - 2Li(x) + C,
where Li(x) is the logarithmic integral function and C is the constant of integration.
Learn more about integrations here:
https://brainly.com/question/30217024
#SPJ1
Please help asap! 20 points for helping and show all work

Answers
28 divided by 3 is 9.3
the answer is 9.3
You are traveling in a car. Your speed is 50 miles per hour. What is your speed in feet per minute?
Answers
Answer:
4399.98 ft per min
Step-by-step explanation:
Divide 50 mi by 60 min = 0.83333Multiply this by 5280 = 4399.9824 ft per minwhat would be your first step in completely factoring 6a^2-15a+6
Answers
The completely factoring form of 6a^2 - 15a + 6 is 3(2a - 1)(a - 2).
To completely factor the expression 6a^2 - 15a + 6, the first step is to check if there is a common factor among the coefficients (6, -15, and 6) and the terms (a^2, a, and 1).
In this case, we can see that the common factor among the coefficients is 3, so we can factor out 3:
3(2a^2 - 5a + 2)
Now we need to factor the quadratic expression inside the parentheses further. We are looking for two binomials that, when multiplied, give us 2a^2 - 5a + 2. The factors of 2a^2 are 2a and a, and the factors of 2 are 2 and 1. We need to find two numbers that multiply to give 2 and add up to -5.
The numbers -2 and -1 fit this criteria, so we can rewrite the expression as:
3(2a - 1)(a - 2)
Therefore, the completely factored form of 6a^2 - 15a + 6 is 3(2a - 1)(a - 2).
for similar questions on factoring.
https://brainly.com/question/28260513
#SPJ8
Convert 10 pounds and 12 ounces to ounces.
Answers
Answer: 172 ounces
Step-by-step explanation:
We are given 10 pounds and 12 ounces to convert to ounces.
There are 16 ounces in 1 pound.
We can create a proportion to find out how much ounces 10 pounds is.
10 pounds / x ounces = 1 pound / 16 ounces
We need to solve for x by isolating the variable x.
10/x = 1/16
10 = x/16
10 * 16 = x
160 ounces = x
so 10 pounds is equivalent to 160 ounces. But we are not done yet.
We were asked to convert 10 pounds and 12 ounces.
So add together the ounces to find the total ounces:
160 ounces + 12 ounces = 172 ounces.
Solve the following systems of linear equations using the method of your choosing.
y = 2x - 1
3y = 6x - 5
Select one:
a.
(2, 5)
b.
Infinite Solutions
c.
No solution
Answers
Answer:
c
Step-by-step explanation:
Substitute the first equation into the second one
3(2x-1)=6x-5
6x-3=6x-5
0=6x-6x-5+3
0=-2
no solution as the variable was canceled out
-1000 2/3 is not real fraction. True or false
Answers
True, While "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
The statement "-1000 2/3 is not a real fraction" is true. A real fraction is a mathematical expression that represents a ratio of two real numbers. In a fraction, the numerator and denominator are both real numbers, and they can be positive, negative, or zero.
In the given statement, "-1000 2/3" is not a valid representation of a fraction. The presence of a space between "-1000" and "2/3" suggests that they are separate entities rather than being part of a single fraction.
To represent a mixed number (a whole number combined with a fraction), a space or a plus sign is typically used between the whole number and the fraction. For example, a valid representation of a mixed number would be "-1000 2/3" or "-1000 + 2/3". However, without the proper formatting, "-1000 2/3" is not considered a real fraction.
It's important to note that "-1000 2/3" can still be expressed as an improper fraction. To convert it into an improper fraction, we multiply the whole number (-1000) by the denominator of the fraction (3) and add the numerator (2). The result would be (-1000 * 3 + 2) / 3 = (-3000 + 2) / 3 = -2998/3.
In conclusion, while "-1000 2/3" is not a real fraction, it can be represented as the improper fraction -2998/3.
for more such question on fraction visit
https://brainly.com/question/30122573
#SPJ8
Evaluate the expression, writing the result as a simplified complex number.
To earn full credit be sure to show all steps and calculations. You may wish to do the work on paper and submit an image of that written work.
\frac{(2+i)(4-2i)}{1+i}
Answers
The simplified expression involving complex numbers is given as follows:
5 + 5i.
What are complex numbers?Complex numbers are number that have a real and an imaginary part, and are defined as follows:
z = a + bi.
In which:
a is the real part.b is the imaginary part.The basic relation of complex numbers is given as follows:
i² = -1.
The fraction for this problem is given as follows:
(2 + i)(4 - 2i)/(1 + i).
The numerator is simplified as follows:
(2 + i)(4 - 2i) = 8 - 4i + 4i - 2i² = 8 + 2 = 10.
Hence the fraction is of:
10/(1 + i).
To remove the complex number from the denominator, the entire fraction is multiplied by the conjugate of the denominator, hence:
10/(1 + i) x (1 - i)/(1 - i) = 10(1 + i)/(1 - i²) = 10(i + 1)/2 = 5 + 5i.
More can be learned about complex numbers at https://brainly.com/question/10662770
#SPJ1
Please help !!!!!! 20 points

Answers
The value of x in the polygon will be 13.25 degrees.
The value of x is 10.
We can find the value of x by plugging in the number of sides of the regular polygon into the formula x = (n-2)*15° - 1.
How to calculate the valueThe sum of the interior angles of a regular polygon with n sides is (n-2) x 180 degrees.
Sum of angles = (24-2) x 180 = 22 x 180 = 3960 degrees
Since all the angles in a regular polygon are congruent, we can divide the sum of the angles by the number of angles to find the measure of one angle:
Measure of one angle = 3960/24 = 165 degrees
165 = 12x + 6
159 = 12x
x = 13.25
Therefore, the value of x is 13.25 degrees.
Each of the triangles in our decomposition has one angle equal to (17x+2)°, so the sum of all the angles in the triangles is 43 × (17x+2)° = 731x+86°.
Therefore, we have:
731x+86° = 7380°
Solving for x, we get:
731x = 7294°
x = 10
Therefore, the value of x is 10.
The equation that can be used to find the value of x is:
(9x+48)° + (15x-24)° = (n-2)*180°
24x + 24 = (n-2)*180°
Dividing both sides by 24, we get:
x + 1 = (n-2)*15°
Subtracting 1 from both sides, we get:
x = (n-2)*15° - 1
Learn more about polygon on
https://brainly.com/question/1592456
#SPJ1
