Answers
Answer:
x = 64
Step-by-step explanation:
The interior angles of a triangle add up to 180 degrees, so the missing angle in the triangle on the right has an angle measurement of 180 - 47 - 81 = 52 degrees.
Since the angle and the rightmost angle in the triangle on the right are vertical angles. They are congruent.
Finally, since the triangle on the left is an isosceles triangle and the base angles, the angles on the top left and bottom left, are congruent and therefore their angle measures are both x degrees. So, 2x + 52 = 180 and x = 64.
Related Questions
The following data show the frequency of rainy days in a year less than 0.01 inch 165 days 0.01 -1 inch 90 days 1.01 - 5 inches 60 days 5.01 -10 inches 40 days more than 10 inches 10 days Find the mode.
Answers
The mode of a dataset is the value that appears most frequently. In this case, we need to find the interval of rainfall that occurs most frequently.
From the given data, we can see that the interval "less than 0.01 inch" has the highest frequency with 165 days. Therefore, the mode of this dataset is "less than 0.01 inch"
Effective communication is crucial in all aspects of life, including personal relationships, business, education, and social interactions. Good communication skills allow individuals to express their thoughts and feelings clearly, listen actively, and respond appropriately. In personal relationships, effective communication fosters mutual understanding, trust, and respect.
In the business world, it is essential for building strong relationships with clients, customers, and colleagues, and for achieving goals and objectives. Good communication also plays a vital role in education, where it facilitates the transfer of knowledge and information from teachers to students.
Moreover, effective communication skills enable individuals to engage in social interactions and build meaningful connections with others. Therefore, it is essential to develop good communication skills to succeed in all aspects of life.
Learn more about dataset here:
https://brainly.com/question/26468794
#SPJ11
The number that belongs in the green box
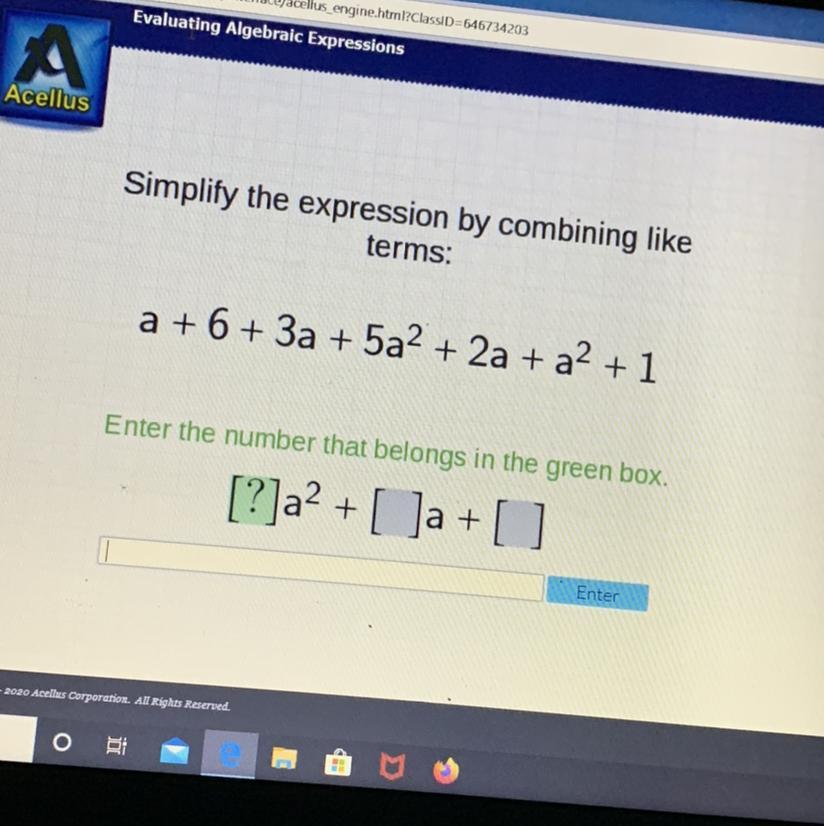
Answers
Answer:
6
Step-by-step explanation:
you combine the a2 with 5a2 as they are the only ones with a squared, combine and you get 6a2 + 6a + 7
Express 13 + 5-14 as a complex number.
Answers
Answer:
the answer is 4
Step-by-step explanation:
Answer:
13+5-14 is equaled to 4 so if i do 18-14 is will still give me 4 because 13+5 is 18 so 18- 14 is 4
Which of the following rational functions is graphed below?
what’s the answer??
Answers
By analyzing the graph's features, you can determine which rational function it represents.
A rational function is a fraction of two polynomial functions, where the denominator is not zero. Rational functions can have vertical asymptotes, where the denominator equals zero and the function is undefined.
They can also have horizontal asymptotes, where the degree of the numerator and denominator functions is equal and the coordinates of the leading term are the same. The graph of a rational function can also have slant asymptotes if the degree of the numerator is one greater than the degree of the denominator.
To determine which rational function is graphed, you need to compare the graph to the standard forms of rational functions. For example, the graph of a rational function y=1/x would have a vertical asymptote at x=0 and would approach the x-axis as it goes to positive and negative infinity. By analyzing the graph's features, you can determine which rational function it represents.
Learn more about coordinates brainly.com/question/16634867
#SPJ11
A chef needs to decorate cupcakes for a birthday party. If the chef places
2
strawberry slices on top of each cupcake, which inequality represents the possible number of cupcakes,
k
, the chef could decorate with
46
strawberry slices?
Answers
The possible number of cupcakes is less than or equal to 23
How to write inequality equation?let
k = possible number of cupcakesNumber of strawberry slices = 46Number if strawberry slices on each cupcake = 2The inequality:
2k ≤ 46
divide both sides by 2
k ≤ 46 / 2
k ≤ 23
Therefore, the possible number of cupcakes is less than or equal to 23
Learn more about inequality:
https://brainly.com/question/25275758
-Solve y = f(x) for x. Then find the input(s) when the output is -10.
F(x) = -7x+6
Answers
-7x+6
thats the answer have fun:)
I NEED HELP ASAP, WILL MARK BRAINLIEST Find the value of y. Round to the nearest tenths place.

Answers
Answer:
Side a = 1
Side b = 0.5
Side c = 0.86603 = √3/2
Nearest tenths is 0.9
Step-by-step explanation:
The following is one way to perform the calculation. It may not be the best way.
Calculates 2 sides based on 3 given angles and 1 side.
b = a·sin(B)/sin(A) = 0.5
c = a·sin(C)/sin(A) = 0.86603 = √3/2
Area =
ab·sin(C)
2
= 0.21651
Perimeter p = a + b + c = 2.36603
Semiperimeter s =
a + b +c
2
= 1.18301
Height ha =
2×Area
a
= 0.43301
Height hb =
2×Area
b
= 0.86603
Height hc =
2×Area
c
= 0.5
Median ma = √(a/2)2 + c2 - ac·cos(B) = 0.5
Median mb = √(b/2)2 + a2 - ab·cos(C) = 0.90139
Median mc = √(c/2)2 + b2 - bc·cos(A) = 0.66144
Inradius r =
Area
s
= 0.18301
Circumradius R =
a
2sin(A)
= 0.5
0.86 is more than 0.85 so the nearest tenths place has to be 0.9
I will also post questions and you please answer them
ANOVA stand for ____________.
a. Another nasty overly vile analysis
b. Analysis of variable averages.
c. Analysis of variance.
d. Analysis of means
Answers
The correct option is c. Analysis of variance.
Why option c is correct?ANOVA stands for Analysis of Variance, which is a statistical method used to test the equality of three or more population means by analyzing the variance between samples.
In an ANOVA, the variance is partitioned into different components, including the variance between groups and the variance within groups. If the variance between groups is larger than the variance within groups, it suggests that there are significant differences between the means of the groups being compared.
ANOVA is commonly used in experimental research to test the effects of one or more independent variables on a dependent variable. It allows researchers to determine whether the means of different groups are significantly different from one another, and if so, which groups are significantly different.
Overall, ANOVA is a powerful statistical tool that enables researchers to test hypotheses and draw conclusions about the differences between multiple groups or treatments.
Learn more about Analysis of Variance
brainly.com/question/30038124
#SPJ11
the lengths of a professor's classes has a continuous uniform distribution between 50.0 min and 52.0 min. if one such class is randomly selected, find the probability that the class length is more than 51.7 min.
Answers
The probability that the class length is more than 51.7 min is 0.3 or 30%.
To solve the problem, we first need to find the total possible outcomes, which is the range of class lengths between 50.0 min and 52.0 min, which is 2.0 min. Since the distribution is uniform, each possible class length within this range is equally likely.
Next, we need to find the favorable outcomes, which is the range of class lengths that are more than 51.7 min. This range is 52.0 min minus 51.7 min, which equals 0.3 min.
To find the probability, we divide the number of favorable outcomes by the total number of possible outcomes:
Probability = (favorable outcomes) / (total outcomes) = 0.3 min / 2.0 min = 0.15 or 15%.
Therefore, the probability of a randomly selected class length being more than 51.7 min is 0.3 or 30%.
To know more about probability, refer here:
https://brainly.com/question/29964401#
#SPJ11
find the divergence of the field f. 13) f = yj - xk ( y 2 x 2) 1/2
Answers
To find the divergence of the vector field f = yj - xk / (y^2 + x^2)^(1/2), we can use the divergence operator, which is defined as the dot product of the gradient operator (∇) and the vector field f.
The gradient operator in Cartesian coordinates is given by ∇ = (∂/∂x)i + (∂/∂y)j + (∂/∂z)k, where i, j, and k are the unit vectors in the x, y, and z directions, respectively. Applying the divergence operator to the vector field f, we have:
div(f) = (∇ ⋅ f) = (∂/∂x)(y/(y^2 + x^2)^(1/2)) + (∂/∂y)(-x/(y^2 + x^2)^(1/2)) + (∂/∂z)(0). Since the vector field f is only defined in the x-y plane, the z-component is zero, and there is no dependence on z.
Taking the partial derivatives, we have:
∂/∂x (y/(y^2 + x^2)^(1/2)) = (y^2 - x^2)/(y^2 + x^2)^(3/2)
∂/∂y (-x/(y^2 + x^2)^(1/2)) = (-xy)/(y^2 + x^2)^(3/2)
Therefore, the divergence of f is given by:
div(f) = (∇ ⋅ f) = (y^2 - x^2)/(y^2 + x^2)^(3/2) + (-xy)/(y^2 + x^2)^(3/2)
Simplifying this expression, we have the divergence of f in terms of x and y.
Note that the divergence measures the net flow or the flux of the vector field through an infinitesimally small volume element. In this case, the divergence gives us information about how the vector field f spreads or converges around a point in the x-y plane.
Learn more about partial derivatives here: brainly.com/question/32234595
#SPJ11
Find the area of the shaded segment of the circle.

Answers
By the way i thought it was cm so i wrote cm its m
Sorry for bad handwriting
if i was helpful Brainliests my answer ^_^

difference between invoice and proforma invoice
Answers
Answer:
An invoice is a commercial instrument that states the total amount due.
The proforma invoice is a declaration by the seller to provide products and services on a specified date and time.
Step-by-step explanation:
May I have Brainliest please? My next rank will be the highest one: A GENIUS! Please help me on this journey to become top of the ranks! I would really appreciate it, and it would make my day! Thank you so much, and have a wonderful rest of your day!
How would this look in standard notation??

Answers
2x + 7 =30, x = 3 true or false
Answers
Answer:
False
Step-by-step explanation:
2x+7=30
2x=23
X= 23/2 or 11.5
X does not equal 3, therefore the statement is false
1) someone help easy math question

Answers
2x + 3x + 20 + 10x - 5 = 10x + 16
What does x equal?
Helpppp and a good explanation, not just the answer pls.
Answers
Answer:x=1 /5
Step-by-step explanation:
Answer:
the right answer is 2ooooooooooooooooooooo
Simplify 5^3/5^7 leaving your anwser in index form
Answers
Steps:
Simplify:
5³/5⁷
= 5³/5⁷
= 5*5*5/ 5*5*5*5*5*5*5
=1/5⁴
=1/625 (Decimal: 0.0016)
Steps by Step:
5³/5⁷
=125/5⁷
=125/78125
=1/625
Answer: =1/625 (Decimal: 0.0016)
Please mark brainliest
Hope this helps.
Show that the process X(t):=e t/2
cos(W(t)),0≤t≤T, is a martingale w.r.t. any filtration for Brownian motion and represent it as an Itô process on any time interval [0,T],T>0.
Answers
A stochastic process X(t) is called a martingale if the expected value of X(t) given all information available up to and including time s is equal to the value of X(s).
Thus, to show that the process X(t):=e^(t/2)cos(W(t)), 0 ≤ t ≤ T is a martingale w.r.t. any filtration for Brownian motion, we need to prove that E(X(t)|F_s) = X(s), where F_s is the sigma-algebra of all events up to time s.
As X(t) is of the form e^(t/2)cos(W(t)), we can use Itô's lemma to obtain the differential form:dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt
Taking the expectation on both sides of this equation gives:E(dX) = E(e^(t/2)cos(W(t))dW) - 1/2 E(e^(t/2)sin(W(t))dt)Now, as E(dW) = 0 and E(dW^2) = dt, the first term of the right-hand side vanishes.
For the second term, we can use the fact that sin(W(t)) is independent of F_s and therefore can be taken outside the conditional expectation:
E(dX) = - 1/2 E(e^(t/2)sin(W(t)))dt = 0Since dX is zero-mean, it follows that X(t) is a martingale w.r.t. any filtration for Brownian motion.
Now, let's represent X(t) as an Itô process on the interval [0,T]. Applying Itô's lemma to X(t) gives:
dX = e^(t/2)cos(W(t))dW - 1/2 e^(t/2)sin(W(t))dt= dM + 1/2 e^(t/2)sin(W(t))dt
where M is a martingale with M(0) = 0.
Thus, X(t) can be represented as an Itô process on [0,T] of the form:
X(t) = M(t) + ∫₀ᵗ 1/2 e^(s/2)sin(W(s))ds
Hence, we have shown that X(t) is a martingale w.r.t. any filtration for Brownian motion and represented it as an Itô process on any time interval [0,T], T > 0.
To know more about martingale visit:
brainly.com/question/32735198
#SPJ11
Let Z be a standard normal variable. Find P(-3.29 < Z < 1.37).
a) 0.9147
b) 0.8936
c) 0.8811
d) 0.9142
e) 0.9035
f) None of the above.
Answers
The cumulative probability up to 1.37 is 0.9142. The correct answer is d) 0.9142
To find P(-3.29 < Z < 1.37), where Z is a standard normal variable, we need to calculate the cumulative probability up to 1.37 and subtract the cumulative probability up to -3.29.
Using a standard normal distribution table or a calculator, we can find:
P(Z < 1.37) ≈ 0.9147 (rounded to four decimal places)
P(Z < -3.29) ≈ 0.0006 (rounded to four decimal places)
To find the desired probability, we subtract the cumulative probability up to -3.29 from the cumulative probability up to 1.37:
P(-3.29 < Z < 1.37) ≈ P(Z < 1.37) - P(Z < -3.29)
≈ 0.9147 - 0.0006
≈ 0.9141
Therefore, the correct answer is d) 0.9142
To know more about probability .
https://brainly.com/question/24756209
#SPJ11
ument will3. Graph and investigate the following piecewise equation: (5points)f(x)={, ?for x < 2(-x + 10 for 2
Answers
We are given the following function:
\(\begin{gathered} f(x)=\lbrace x^2;\text{ x<2} \\ -x+10;2\le x\le6\} \end{gathered}\)The graph of this equation is a parabola for values of x < 2 and a line for values of 2<= x <= 6. The graph is the following:
Which statements hold true for the function?
f(x) = 3x² - 5
Of(5)
Of(0)=1
f(5)<1
Of(3)
Answers
The statements for the function f( x) = 3x ²- 5 are
f( 5)< 1( false)
f( 0) = 1( false)
Statements for the function f(x) = 3x ²- 5
To find the true or false statement we have to substitute the value for x
First, x= 3
f(x) = 3x ²- 5
f(3)= 3( 5)²- 5
f(3) = 75- 5
f(3)= 70.
Thus, the statement" f( 5)< 1" is false.
Now, at x =0
f(x) = 3x ²- 5
f(0) = 3( 0)²- 5
f(0)= 0- 5
f(0)= -5.
Thus, the statement" f( 0) = 1" is false.
Learn more about Function here:
https://brainly.com/question/30721594
#SPJ1
a cylindrical container must hold 2l or 2,000 cm^3 of liquid. find the dimensions of the container which will minimize the amount of material needed.
Answers
The dimensions of the container is r = 6.828 cm and h = 13.656 cm.
Volume of the Cone:
Volume of the cone is define the space or the capacity of the cone.
The formula for the volume of the cone is,
V = πr²h
Where
r represents the radius of the cone
h represents the height of the cone
Given,
Cylindrical container must hold 2l or 2,000 cm³ of liquid.
Here we need to find the dimensions of the container which will minimize the amount of material needed.
Let height = h and radius of the base = r.
We know that the volume of the container,
V = 2000
We know the formula of volume of the cone is,
V = πr²h
2000 = πr²h
Here we need the value of h,
So,
h = 2000/πr²
and surface area of the can
S = 2πr² + 2πrh
Apply the value of h,
S = 2πr² + 2πr (2000/πr²)
S = 2πr²+ (4000/r)
S = 2πr²+ 4000 x r⁻¹
S′=(−1)(4000r⁻²)+4πr
S′=4πr−(4000/r²)
Consider,
4πr−(4000/r²) = 0
4πr³−4000 = 0
πr³−1000 = 0
πr³ = 1000
r³ = 1000 / π
r = √1000 / π
r = 6.828 cm
Apply the value of r on the equation to find the value of h,
h = 2000/(π∗(6.828)²)
h = 2000/146.46
h = 13.656
To know more about the Volume of the cone here
https://brainly.com/question/1984638
#SPJ4
I will give anyone the brainliest correctly

Answers
Step-by-step explanation:
2% 0.2 1/3 0.8 3
these are the numebrs after being converted
0.02 0.2 0.3333 0.8 3
Evaluate the quantity 3 squared times 3 to the power of negative 5 end quantity over 5 to the power of negative two.
Answers
16/27 is the value of quantity.
What is a linear equation in math?
A linear equation only has one or two variables. No variable in a linear equation is raised to a power greater than 1 or used as the denominator of a fraction. When you find pairs of values that make a linear equation true and plot those pairs on a coordinate grid, all of the points lie on the same line.There are three major forms of linear equations: point-slope form, standard form, and slope-intercept form. We review all three in this article.Some of the examples of linear equations are 2x – 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, 3x – y + z = 3.\(\frac{3^{2} * 3^{-5} }{4^{2} } = \frac{3^{-3} }{4^{-2} }\)
\(\frac{1}{3^{3} }\) ÷ \(\frac{1}{4^{2} }\)
\(\frac{1}{27} * 16 = \frac{16}{27}\)
Learn more about linear equation
brainly.com/question/11897796
#SPJ4
a circular cake is split into four quarters. if the diameter of the cake is 25 cm, how long is the perimeter of each piece?
Answers
Answer:
(6.25\(\pi\) + 25)cm is the exact answer
44.625 cm is an approximation
Step-by-step explanation:
c = circumference (perimeter)
d = diameter
C = \(\frac{\pi d}{4}\)
C = \(\frac{25\pi }{4}\) = 6.25\(\pi\) This is the exact answer
That would be the curved part of the pi. Then we need to add the 2 sides which would be \(\frac{25}{2}\) + \(\frac{25}{2}\) = \(\frac{50}{2}\) = 25 The sides are the length of the radius which is half of the diameter.
(6.25\(\pi\) + 25)cm is the exact answer
If we use 3.14 for \(\pi\) The approximate answer would be:
6.25(3.14) + 25
19.625 + 25
44.625 cm is an approximation
captain rusczyk tracked down a pirate who had stolen $2345 {6}$ dollars worth of goods from his ship. after winning an epic duel, the captain demands that the pirate return $41324 {5}$ dollars. how much has the pirate gone in debt due to his encounter with rusczyk? express your answer in base $10$.
Answers
The pirate has gone into debt by $38,979 in base 10 due to his encounter with Captain Rusczyk.
To determine the amount of debt, we need to calculate the difference between the value of the goods the pirate stole and the amount demanded by Captain Rusczyk. The pirate initially stole $2345_6, which means it is in base 6. Converting this to base 10, we have $2\times6^3 + 3\times6^2 + 4\times6^1 + 5\times6^0 = 2\times216 + 3\times36 + 4\times6 + 5\times1 = 432 + 108 + 24 + 5 = 569$.
Captain Rusczyk demanded $41324_5, which means it is in base 5. Converting this to base 10, we have $4\times5^4 + 1\times5^3 + 3\times5^2 + 2\times5^1 + 4\times5^0 = 4\times625 + 1\times125 + 3\times25 + 2\times5 + 4\times1 = 2500 + 125 + 75 + 10 + 4 = 2714$.
Therefore, the pirate has gone into debt by $569 - 2714 = -2145$. Since the pirate owes money, we consider it as a negative value, so the pirate has gone into debt by $38,979 in base 10.
Learn more about negative numbers here: brainly.com/question/258076
#SPJ11
I need help pleaseee!!

Answers
Step-by-step explanation:
step 1. Range refers to y values
step 2. The range includes -4 and excludes 9
step 3. (9, -4] is the answer.
5×12÷[-12÷{15+(4-3)}]
Answers
Answer: -80
Step-by-step explanation:
for which of the three intervals do you have the most con dence that it captures the population mean ?
Answers
To determine which interval has the most confidence in capturing the population mean, we need to look at the confidence level associated with each interval. A confidence interval is a range of values that we believe contains the true population parameter.
If we have three intervals with different confidence levels, the interval with the highest confidence level would be the one with the most confidence in capturing the population mean. For example, if Interval A has a confidence level of 90%, Interval B has a confidence level of 95%, and Interval C has a confidence level of 99%, then Interval C would have the most confidence in capturing the population mean.
It's important to note that the level of confidence we choose affects the width of the interval. The higher the confidence level, the wider the interval will be. Therefore, we need to balance the desire for a high level of confidence with the need for a narrow interval.
In summary, the interval with the highest confidence level is the one with the most confidence in capturing the population mean. Confidence intervals are a powerful tool in statistics that allows us to estimate population parameters from a sample with a known degree of uncertainty.
learn more about population parameters here: brainly.com/question/30280261
#SPJ11
A manager uses the following linear trend equation to predict monthly receipts: \( Y_{t}=3,700+300 t \). What is the forecast for October of this year if \( \mathrm{t}=0 \) was July of this year?
Answers
The linear trend equation to predict monthly receipts is given by: $$Y_{t}=3,700+300t$$ where Y is the predicted monthly receipt and t is the time period in months where t=0 is July this year.
To forecast the receipt for October, we need to find the value of Y when t=3 (since t=0 corresponds to July, August would be t=1, September would be t=2, and October would be t=3).Therefore, we can substitute t=3 in the equation above to get: $$Y_{3}=3,700+300(3)$$$$Y_{3}=3,700+900$$$$Y_{3}=4,600$$
Therefore, the forecast for October of this year is $4,600. The linear trend equation to predict monthly receipts is given by: $$Y_{t}=3,700+300t$$ where Y is the predicted monthly receipt and t is the time period in months where t=0 is July this year. The answer to the given question is: The forecast for October of this year is $4,600.
To know more about equation visit:
https://brainly.com/question/29657988
#SPJ11
