Answers
Answer:
Here we will use the relationships:
\(a^n*a^m = a^{n + m}\)
\((a^n)^m = a^{n*m}\)
\(\frac{a^n}{a^m} = a^{n - m}\)
And a number:
\(a^n\)
is between 0 and 1 if a is positive and larger than 1, and n is negative.
if a is positive and 0 < a < 1, then we need to have n positive such that:
0 < a^n < 1
A) \(5^3*5^{-4} = 5^{3 + (-4)} = 5^{-1}\)
This is between zero and 1,
B) \(\frac{3^5}{3^{-6}} = 3^{5 - (-6)} = 3^{11}\)
This is greater than 1, because the exponent is positive.
C) \((\frac{1}{4})^3*( \frac{1}{4})^2 = (\frac{1}{4})^{2 + 3} = (\frac{1}{4})^5\)
Because a is smaller than 1, and the exponent is positive, then the expression is between 0 and 1.
D) \(\frac{(-7)^5}{(-7)^7} = (-7)^{5 - 7} = -7^{-2}\)
The exponent is negative (and pair) then the expression is between 0 and 1.
Remember that when the exponent is pair, we always have that:
(-N)^m = (N)^m
So (-7)^-2 = 7^-2
Related Questions
What is the predicted gpa for a student who sleeps 2.5 hours per day? answer choices are rounded to the hundredths place.
Answers
The predicted GPA of the student who sleeps for 2.5 hours per day is 2.27; option D.
What is the predicted GPA for the student as obtained from the scatter plot?The GPA of a student refers to the grade point average of the student which is the average of the student's grade points in his or her courses.
The predicted GPA of the student who sleeps for 2.5 hours per day is obtained from the scatter plot given below:
The equation for the least squares regression line is y = 0.375x + 1.33
x = 2.5
y = 0.375 * 2.5 + 1.33
y = 2.27
In conclusion, the predicted GPA for the student is obtained from the scatter plot.
Learn more about scatter plot at: https://brainly.com/question/6592115
#SPJ4

Answer:
2.27
Step-by-step explanation:
Got it right on the test.
whats the slope intercept form of y=3x-2
Answers
Y intercept: (0,-2)
suppose bill gets lucky on his next hunting trip and shoots 14 ducks using the same amount of shotgun shells he used on his previous hunting trip to bag 8 ducks. how much would it have cost him to shoot the last six ducks?
Answers
By using the unitary method , the cost of one shotgun shell to determine that the cost of shooting the last 6 ducks would be $6.86.
The unitary method involves finding the value of one unit and then using that value to find the value of a given number of units. In this problem, we can use the number of shotgun shells as the unit of measurement. Let's say Bill used x shotgun shells to shoot 8 ducks on his previous hunting trip. Therefore, the cost of shooting 8 ducks would be the cost of x shotgun shells.
Now, we know that Bill shot 14 ducks using the same amount of shotgun shells he used on his previous trip. Therefore, the cost of shooting 14 ducks would be the cost of x shotgun shells. We can use a proportion to find the value of x.
8 ducks can be shot using x shotgun shells, so 14 ducks can be shot using (14/8) x x shotgun shells.
Simplifying this expression, we get:
(14/8) x x = 14 ducks
x = (8/14) x 14 ducks
x = 8/7 ducks
So, Bill used 8/7 shotgun shells to shoot 1 duck on his previous hunting trip.
Now, to find the cost of shooting the last 6 ducks, we need to determine how many shotgun shells he would need. Using the unitary method again, we can say:
1 duck can be shot using 8/7 shotgun shells, so 6 ducks can be shot using 6 * (8/7) shotgun shells.
Simplifying this expression, we get:
6 x (8/7) = 48/7 shotgun shells
Therefore, to shoot the last 6 ducks, Bill would need 48/7 shotgun shells. To determine the cost, we need to know the cost of one shotgun shell. Let's say the cost of one shotgun shell is $1. Then the cost of shooting the last 6 ducks would be:
(48/7) x $1 = $6.86 (rounded to the nearest cent)
To know more about unitary method here
https://brainly.com/question/28276953
#SPJ4
according to the rational root theorem, which function has the same set of potential rational roots as the function g(x)
Answers
Option (A)'s f(x) = 3x⁵ -2x⁴ - 9x³ + x² -12 has the same set of potential rational roots as the given function g(x).
What are roots of an equation?Roots of an equation refer to the values that when put into the variable of the equation, satisfy the equation and give the required value as 0.
Given:
g(x) = 3x⁵ - 2x⁴ + 9x³ - x² + 12 = 0
To find: Function having same set of potential rational roots as g(x).
Finding:
Finding the rational roots of g(x):Let 'm' denote the rational roots of 12.=> Then, m = ±1, ±2, ±3, ±4, ±6
2. Let 'n' denote the rational roots of 3.
=> Then n = ±1, ±3
Hence, the rational roots \(\frac{m}{n}\) will be given by: ±1, ±2, ±3, ±4, ±6, ±\(\frac{1}{3}\), ±\(\frac{2}{3}\), ±\(\frac{4}{3}\).
Now, in the Option A's equation: f(x) = 3x⁵ -2x⁴ - 9x³ + x² -12,The rational roots will be taken of 12 and 3 in the same position as in g(x).
Hence, the rational roots of f(x) will also be given by: ±1, ±2, ±3, ±4, ±6, ±\(\frac{1}{3}\), ±\(\frac{2}{3}\), ±\(\frac{4}{3}\).
Thus, Option (A)'s f(x) = 3x⁵ -2x⁴ - 9x³ + x² -12 has the same set of potential rational roots as the given function g(x).
To learn more about roots of an equation , refer to the link: https://brainly.com/question/25841119
#SPJ4
(COMPLETE QUESTION:
According to the Rational Root Theorem, which function has the same set of potential rational roots as the function g(x) = 3x5 – 2x4 + 9x3 – x2 + 12?
A).f(x) = 3x5 – 2x4 – 9x3 + x2 – 12
B).f(x) = 3x6 – 2x5 + 9x4 – x3 + 12x
C).f(x) = 12x5 – 2x4 + 9x3 – x2 + 3
D).f(x) = 12x5 – 8x4 + 36x3 – 4x2 + 48)
How many terms are in this expression 4u + 6t
Answers
Answer:
There are two terms in the expression...
Hope this helps!!!!
a line has a slope of 6 and an x-intercept of 7
write the equation for the line slope-intercept form
Answers
Answer:
y = 6x - 42
Step-by-step explanation:
Point (7,0)
y-intercept = 0 - (6)(7) = -42
I need help!!!!!!!!!!!!!!!
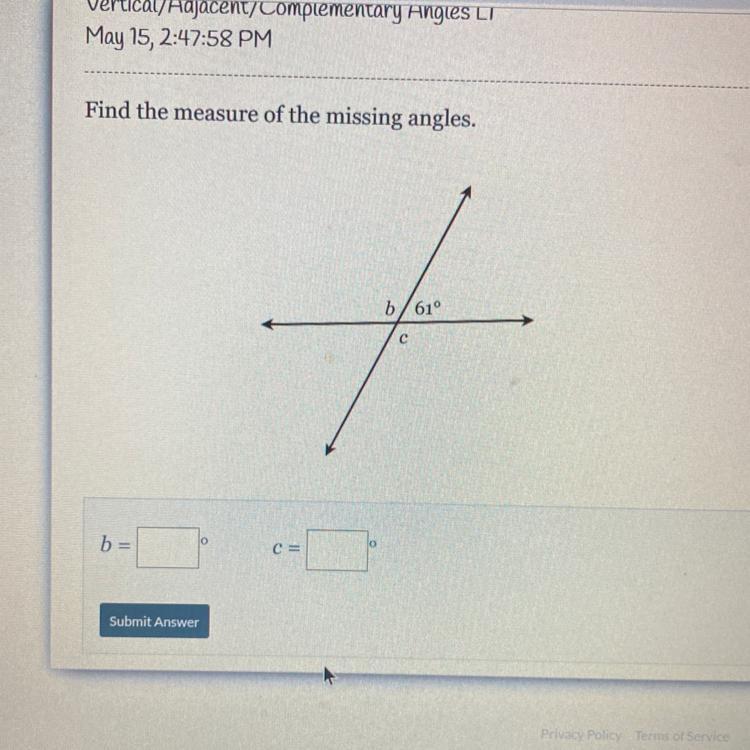
Answers
Answer:
B=c=119
Step-by-step explanation:
B=180-61=119
C=B=119
When n is divided by 3, the remainder is 1 What is the remainder when 2n is divided by 3
Answers
Answer:
Only n if 2n is/3 when 2nis divide by 3
Answer:3
Step-by-step explanation:
you could only divide 2n in 3 was there so it would be three
a tank contains 100 gal of pure water inirially. a solution containing zib salt /gal enters into the tank at the vate of 3 gal/min. also a drain is open so that qhe volume of the solution is constant. tow much after salt is in the tank after 60 mins?
Answers
To determine the amount of salt in the tank after 60 minutes, we need the concentration of salt in the solution entering the tank.
The information provided, which is the salt concentration in terms of "zib salt /gal," is incomplete and does not specify the actual value of zib.
If you can provide the concentration of salt in the solution entering the tank (in terms of a specific numerical value), I can help you calculate the amount of salt in the tank after 60 minutes.
Know more about salt concentration here:
https://brainly.com/question/30105881
#SPJ11
a tank contains 100 gal of pure water inirially. a solution containing zib salt /gal enters into the tank at the vate of 3 gal/min. also a drain is open so that qhe volume of the solution is constant. tow much after salt is in the tank after 60 mins?
Consider the linear function y= 10x + 2 and the linear function with a slope of 2 and a y-intercept of 10. Which of these statements is correct?

Answers
Answer:
C y=10x+2 has a greater rate of change
Step-by-step explanation:
y= 10x + 2 has greater slope than the linear function with a slope of 2 and a y-intercept of 10. Thus, option C) is correct.
Slope is defined as the rate of change in one variable with respect to other.
Given the following:
First linear function y= 10x + 2.......................1
Slope=10 and intercept=2
Second linear function with a slope of 2 and a y-intercept of 10 that is
y=2x+10......................................................2
Slope=2 and intercept=10
First statement:
Line 1 has greater intercept is false as 2<10.
Second statement:
Two function have intercept is false as both have different intercept as
2≠10.
Third statement:
Line 1 has greater slope is true as 10>2.
Thus, option C) is correct.
Learn more about slope, here:
https://brainly.com/question/29044610
#SPJ6
Craig is learning to identify local birds with a Field Guide to Forest Birds deck of cards. He randomly selects one card from the deck, puts it back in the deck, and selects another card. He repeats this several times and gets 4 hummingbirds, 3 falcons, 1 woodpecker, 4 owls, 3 loons, and 2 eagles.
Based on the data, what is the probability that the next card Craig selects will be a falcon card?
Answers
The probability that the next card Craig selects will be a falcon card is 3/17.
Given that, Craig gets 4 hummingbirds, 3 falcons, 1 woodpecker, 4 owls, 3 loons, and 2 eagles.
Here, the total number of outcomes = 4+3+1+4+3+3=17
Number of favorable outcomes = 3
Now, probability of an event = 3/17
Therefore, the probability that the next card Craig selects will be a falcon card is 3/17.
To learn more about the probability visit:
https://brainly.com/question/11234923.
#SPJ1
Find the value of x.

Answers
Answer:
x = 3.5
Step-by-step explanation:
\(\frac{4}{7}\) = \(\frac{2}{x}\)
4x = 14
x = 3.5
7x=28
28/7 = 4
x=4
Levi is planning a road trip. He throws a dart on a map of the United States to decide where to go. There are 4 states that start with the letter A, 3 states that start with the letter C, and 8 states that start with the letter M. What is the probability that Levi throws a dart on a state that starts with an A or an M? (Hint: There are 50 total states.)
P(A∪M)=
1) 0.01
2) 0.24
3) 0.64
4) 0.42
Answers
Answer:
since there are 4 states that start with A and 8 that start with M, this means that out of the 50 states there are 12 states that he could throw a dart at and get either A or M, meaning that 12/50 is the fraction and 12/50 converted into a percentage or decimal is 0.24 meaning that 0.24 is the probability that he throws a dart and hits a state that starts with an A or M
Keep getting the answer wrong

Answers
Answer:
20
Step-by-step explanation:
find h(x, y) = g(f(x, y)). g(t) = t2 t , f(x, y) = 7x 6y − 42
Answers
Therefore, h(x, y) = 49x^3 - 294x^2y + 441xy^2 - 252x^2 + 252xy - 588y^2 + 294x - 252y - 1764.
To find h(x, y) = g(f(x, y)), we first need to evaluate f(x, y) and then use the result as input for g(t).
Starting with f(x, y), we have:
f(x, y) = 7x - 6y - 42
Next, we need to use this as input for g(t), which is defined as:
g(t) = t^2*t
Substituting f(x, y) for t, we get:
g(f(x, y)) = (7x - 6y - 42)^2*(7x - 6y - 42)
Simplifying this expression, we can expand the square and get:
h(x, y) = 49x^3 - 294x^2y + 441xy^2 - 252x^2 + 252xy - 588y^2 + 294x - 252y - 1764
Therefore, h(x, y) = 49x^3 - 294x^2y + 441xy^2 - 252x^2 + 252xy - 588y^2 + 294x - 252y - 1764.
To know more about evaluate visit:
https://brainly.com/question/12837686
#SPJ11
a horizontal beam safely supports a load P that varies jointly as the product of the width W of the beam and the square of the depth D and inversely as the length L. a beam that has a width of 5in., depth of 12in., and length of 8in., can safely support 1260 lb. determine the safe load in pounds of a beam made from the same material if the beam is 20in. long
Answers
The Final Safe load = 6010.144 lbs.
What is unitary method?The unitary technique involves first determining the value of a single unit, followed by the value of the necessary number of units. What can be values and units.Let's say you go to the store to buy six apples. You are informed by the shopkeeper that he is offering 10 apples for Rs 100. In this instance, the value and the units are the price of the apples.Recognizing the units and values is crucial when using the unitary technique to a problem.Always write the items that need to be computed on the right side and the things that are known on the left side to simplify things.We are aware of the quantity of apples and the amount of money in the aforesaid problem.According to our question-
inverse proportionality means L = k/l
So the equation is:
L = k(wd2/l)
You are given:
w = 6 in
d = 5 in
l = 12 ft
L = 7666 lbs
7666 = k(6*52/12)
Solve for the constant, k.
7666 = k (6*25/12)
7666 = k (150/12)
7666 = k (12.5)
613.28 lbs/(ft.in3) = k
Use this k-value to solve for L in the last part of the question.
What safe load, L would a beam 3 in. wide, 7 in. deep and 15 ft long of the same material support? (Round off your answer to the nearest pound.)
w = 3 in
d =7 in
l = 15 ft
k = 613.28 l b s /(ft.in3)
learn more about unitary method click here:
brainly.com/question/24587372
#SPJ1
How many different posets, totally ordered,
well-ordered relations are there on a set of size n.
Answers
A partially ordered set (poset) on a set of size n is a set of elements with a relation among them that is reflexive, antisymmetric and transitive. In a poset, for any two elements x and y, one of the following conditions must be satisfied: x ≤ y, y ≤ x or neither x ≤ y nor y ≤ x.
The number of different posets on a set of size n is equal to the nth Bell number (Bn). The nth Bell number is defined as the number of ways that a set of n elements can be partitioned into non-empty subsets. Hence, the number of different posets on a set of size n is Bn.Likewise, a totally ordered set (or linearly ordered set) is a poset in which every pair of elements is comparable, i.e., either x ≤ y or y ≤ x. The number of different totally ordered sets on a set of size n is equal to the factorial of n, denoted by n!.Lastly, a well-ordered set is a totally ordered set in which every non-empty subset has a least element
. The number of different well-ordered sets on a set of size n is equal to the nth Bell number (Bn) as well. herefore, to answer the question, the number of different posets, totally ordered and well-ordered relations on a set of size n are as follows: Posets: Bn Totally ordered sets: n Well-ordered sets.
To know more about ordered set (poset) visit:-
https://brainly.com/question/33191427
#SPJ11
please help meee i need all the answers
Answers
The answers to all parts are shown below.
1. The number of ways are
= 11!/ (11-1)!
= 11! /10!
= 11
2. The favorable outcomes of the event
Triangle= 1
star = 4
Not square= 9
Not circle= 8
3. C( 12, 1)= 12!/ 1! 11!
= 12 ways
4. Choose a cat = C(18, 12)= 18! / 12! 6!
= 18564
5. Choose a dog
= C(18, 6)
= 18!/ 6! 12!
= 18564
6. Bus arrive on time= 1-2/7 = 5/7
Learn more about Combination here:
https://brainly.com/question/29594894
#SPJ1
A metallurgist needs to make 12.4 lb. of an alloy containing 50% gold. he is going to melt and combine one metal that is 60% gold with another metal that is 40% gold. how much of each should he use? show all work.
Answers
To find out how much of each metal the metallurgist should use to make the alloy, we can set up an equation based on the percentage of gold in each metal. Let's assume the metallurgist uses x pounds of the metal that is 60% gold, and y pounds of the metal that is 40% gold.
The metallurgist should use 6.2 pounds of the metal that is 60% gold and 6.2 pounds of the metal that is 40% gold to make 12.4 pounds of the alloy containing 50% gold.
The total weight of the alloy is 12.4 pounds, so we have the equation:
x + y = 12.4
Now, let's consider the percentage of gold in the alloy. The alloy needs to contain 50% gold.
The metal that is 60% gold will contribute 60% of x pounds of gold, which is 0.6x pounds of gold.
The metal that is 40% gold will contribute 40% of y pounds of gold, which is 0.4y pounds of gold.
Since the alloy needs to contain 50% gold, the total amount of gold in the alloy will be 50% of the total weight, which is 0.5 times 12.4 pounds:
0.5 * 12.4 = 6.2 pounds of gold
Now, we have another equation:
0.6x + 0.4y = 6.2
We have a system of two equations:
x + y = 12.4
0.6x + 0.4y = 6.2
To solve this system, we can use substitution or elimination. I will use the elimination method.
First, let's multiply the first equation by 0.4 to make the coefficients of y in both equations the same:
0.4(x + y) = 0.4 * 12.4
0.4x + 0.4y = 4.96
Now, we can subtract the second equation from this new equation to eliminate y:
(0.4x + 0.4y) - (0.6x + 0.4y) = 4.96 - 6.2
0.4x - 0.6x = -1.24
-0.2x = -1.24
x = -1.24 / -0.2
x = 6.2
Substituting this value of x back into the first equation:
6.2 + y = 12.4
y = 12.4 - 6.2
y = 6.2
So, the metallurgist should use 6.2 pounds of the metal that is 60% gold and 6.2 pounds of the metal that is 40% gold to make 12.4 pounds of the alloy containing 50% gold.
Learn more about solving equations here:
https://brainly.com/question/17145398
#SPJ11
Solve the right triangle for all unknown sides and angles. Round your answers to two decimal places.
B = 71
, b = 24
Answers
Angle A is 19 degrees.
Angle C is 90 degrees.
Side a is approximately 7.83.
Side c is approximately 34.50.
To solve the right triangle given that B = 71 degrees and b = 24, we can use the trigonometric ratios sine, cosine, and tangent.
Finding Angle A:
Angle A is the complementary angle to B in a right triangle, so we can calculate it using the equation:
A = 90 - B
Substituting the given value, we have:
A = 90 - 71
A = 19 degrees
Therefore, Angle A is 19 degrees.
Finding Angle C:
Since it is a right triangle, Angle C is always 90 degrees.
Therefore, Angle C is 90 degrees.
Finding Side a:
We can use the sine ratio to find the length of side a:
sin(A) = a / b
Rearranging the equation to solve for a, we have:
a = b * sin(A)
Substituting the given values, we have:
a = 24 * sin(19)
a ≈ 7.83
Therefore, the length of side a is approximately 7.83.
Finding Side c:
Using the Pythagorean theorem, we can find the length of side c:
c^2 = a^2 + b^2
Substituting the given values, we have:
c^2 = 7.83^2 + 24^2
c^2 ≈ 613.68 + 576
c^2 ≈ 1189.68
Taking the square root of both sides to solve for c, we have:
c ≈ √1189.68
c ≈ 34.50
Therefore, the length of side c is approximately 34.50.
To know more about trigonometric ratios, visit
https://brainly.com/question/23130410
#SPJ11
Find the y-intercept of the following equation. Simplify your answer.
y
=
9
10
x
+
7
6
y-intercept =

Answers
Answer:
Brainliest!Step-by-step explanation:
the equation is y=mx+b
the b part is the y-intercept
so in your equation... the y=intercept would be 7/6
7. Find the corresponding angle.
(look at the picture)

Answers
Answer:
angle SXV
Step-by-step explanation:
Please help much appreciate!

Answers
12.4 is 20% of what number?
A. 2.48
B. 32.4
C. 62
D. 248
Answers
Answer:
c
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
put 12.4* 20 and you get D
Are the two triangles below similar? (1 point)
01) Yes; they have congruent corresponding angles
0 2) No; they do not have congruent corresponding angles
3) Yes; they have proportional corresponding sides
04) No; they do not have proportional corresponding sides

Answers
Answer:
Yes they jave proportional corresponding sides
Hey help me please, and have a great day!!

Answers
Answer:
It should be 49.7 degrees F.
Step-by-step explanation:
Thank you and have a great day too. Also really its just 58.1 minus 1.2 7 times or 58.1 minus 1.2 times 7
Carrie Ann has a penny bank with 812 pennies in it. She gave her little sister 10 pennies to start her own penny bank savings. She gave 68 pennies to her brother in exchange for taking her turn at doing the dishes. How many pennies does Carrie Ann have in her penny bank? Explain how you got your answer.
Answers
Answer:
Just do 812-78 that equals 734.
Answer:
734 pennies
Step-by-step explanation:
10 +68 =78 pennies that she gave to her sister and her brother
812 - 78 =734 pennies has
find the mean, lower quartile, and highest quartile of 53, 49, 52, 71, 67, 51, 63, 49, 58
Answers
Answer:
the mean is 61.44, the lower quartile is 51, and the upper quartile is 65
Step-by-step explanation:
we need to first sort the data in ascending order:
49, 49, 51, 52, 53, 58, 63, 67, 71
The mean is the average of all the numbers in the data set:
Mean = (49 + 49 + 51 + 52 + 53 + 58 + 63 + 67 + 71) / 9 = 553 / 9 = 61.44 (rounded to two decimal places)
To find the lower quartile, we need to find the median of the lower half of the data set. Since there are an odd number of values in the data set, we exclude the median value from the lower half. The lower half of the data set is:
49, 49, 51, 52, 53
The median of the lower half is the middle value, which is 51. Therefore, the lower quartile is 51.
To find the upper quartile, we need to find the median of the upper half of the data set. Again, we exclude the median value from the upper half since there are an odd number of values. The upper half of the data set is:
58, 63, 67, 71
The median of the upper half is the middle value, which is (63 + 67) / 2 = 65. Therefore, the upper quartile is 65.
Answer: Lower quartile=51.5, mean=58, and highest quartile=65.
Step-by-step explanation: To find the lower quartile you have to find the median of the lower half. In this case, the lower half is 49, 51, 52, and 53. Since there are two numbers, we have to find the average of them (51, 52). To find the average, add them together, which would be 103. Now, divide 103 by 2 which would be 51.5 (the lower quartile). To find the mean, add all the numbers together (464) and divide them by the number of numbers that are on there (8). So, 464/8 is 58. To find the highest quartile, find the median of the upper half. In this case, we have find the average of 63 and 67. So, add 63 and 67 which would be 130, and divide by 2 (which would be 65). Hope this helped and have a great day!
In your reservoir, you have a production well which flows for 48 hours at 200 STB/day, and then shut-in for 24 hours. The following additional data are given : Pi = 3100 psi Ct = 15x10^-6 psi^-1 Bo = 1.3 bbl/STB ϕ = 15% μ=1.2 cp K = 45 md and h = 60 ft
a-) Calculate the pressure in this production well at 12 hours of shut in
b-) Explain how can you use superposition in time to analyze a pressure build-up test.
Answers
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
We have,
a) To calculate the pressure in the production well at 12 hours of a shut-in, we can use the equation for pressure transient analysis during shut-in periods, known as the pressure buildup equation:
P(t) = Pi + (Q / (4πKh)) * log((0.14ϕμCt(t + Δt)) / (Bo(ΔP + Δt)))
Where:
P(t) = Pressure at time t
Pi = Initial reservoir pressure
Q = Flow rate
K = Permeability
h = Reservoir thickness
ϕ = Porosity
μ = Viscosity
Ct = Total compressibility
t = Shut-in time (12 hours)
Δt = Time since the start of the flow period
Bo = Oil formation volume factor
ΔP = Pressure drop during the flow period
Given:
Pi = 3100 psi
Q = 200 STB/day
K = 45 md
h = 60 ft
ϕ = 15%
μ = 1.2 cp
Ct = 15x10^-6 psi^-1
Bo = 1.3 bbl/STB
t = 12 hours
Δt = 48 hours
ΔP = Pi - P(t=Δt) = Pi - (Q / (4πKh)) * log((0.14ϕμCt(Δt + Δt)) / (Bo(ΔP + Δt)))
Substituting the given values into the equation:
ΔP = 3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15x\(10^{-6}\) * (48 + 48)) / (1.3 * (3100 - (200 / (4π * 45 * 60)) * log((0.14 * 0.15 * 1.2 * 15 x \(10^{-6}\) * (48 + 48)) / (1.3 * (0 + 48))))))
After evaluating the equation, we can find the pressure in the production well at 12 hours of shut-in.
b) Superposition in time is a principle used in pressure transient analysis to analyze and interpret pressure build-up tests.
It involves adding or superimposing the responses of multiple transient tests to simulate the pressure behavior of a reservoir.
The principle of superposition states that the response of a reservoir to a series of pressure changes is the sum of the individual responses to each change.
Superposition allows us to combine the information obtained from multiple tests and obtain a more comprehensive understanding of the reservoir's behavior and properties.
It is a powerful technique used in reservoir engineering to optimize production strategies and make informed decisions regarding reservoir management.
Thus,
a) To calculate the pressure at 12 hours of shut-in:
substitute the given values into the pressure buildup equation and solve for P(t=12).
b) Superposition in time is used in pressure buildup analysis by adding or summing the responses of multiple transient tests to analyze and interpret reservoir behavior and properties.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ12
An airline claims that there is a 0.10 probability that a coach-class ticket holder who flies frequently will be upgraded to first class on any flight. This outcome is independent from flight to flight. Sam is a frequent flier who always purchases coach-class tickets.
Answers
The probability that Sam's first upgrade will occur after the third flight = 0.729
Let m represents the number of flights Sam must take in order to receive his first upgrade.
To find the probability that Sam's first upgrade will occur after the third flight.
i.e., to find P(m ≥ 4)
Here, 0.10 probability that a coach-class ticket holder who flies frequently will be upgraded to first class on any flight.
p = 0.10
q = 1 - p
q = 0.90
P(m ≥ 4) = 1 - P(m ≤ 3)
P(m ≥ 4) = 1 - [P(m = 1) + P(m = 2) + P(m = 3)]
P(m ≥ 4) = 1 - [0.1 + (0.9 × 0.1) + (0.9² × 0.1)]
P(m ≥ 4) = 1 - (0.1 + 0.09 + 0.081)
P(m ≥ 4) = 0.729
therefore, the required probability = 0.729
Learn more about the probability here:
https://brainly.com/question/15124899
#SPJ4
The complete question is:
An airline claims that there is a 0.10
probability that a coach-class ticket holder who flies frequently will be upgraded to first class on any flight. This outcome is independent from flight to flight. Sam is a frequent flier who always purchases coach-class tickets.
What is the probability that Sam's first upgrade will occur after the third flight?
