Answers
Step-by-step explanation:
please mark me as brainlest

Related Questions
W=0+4T
640-7t=W
Please help me
Answers
Answer:
2560/11
Step-by-step explanation:
�
=
640
11
and
�
=
2560
11
the function has zeros at -1 and -11, and a minimum at -5
Answers
The minimum point on the graph is \((-6,25)\), which confirms that the function has a minimum at\(-6\).
What is graph?In mathematics, a graph is a diagram that shows the relationship between different sets of data. It is made up of points, which are also called vertices or nodes, that are connected by lines or curves called edges or arcs.
In mathematics, a function is a relation between two sets of data, such that each input in the first set corresponds to exactly one output in the second set. In other words, a function maps each input value to exactly one output value.
According to given information:
Let's start by writing the quadratic function in factored form, given that it has zeros at \(-1\) and \(-11\):
\(f(x) = a(x- (-1))(x- (-11))\)
Simplifying, we get:
\(f(x) = a(x+1)(x+11)\)
To find the value of a, we need to use the fact that the function has a minimum at \(-5\). Since the vertex of the parabola is at the minimum point, we know that the x-coordinate of the vertex is \(-5\). Therefore, we can use this information to find the value of a as follows:
\(-5 = (-1+(-11))/2\\-5 = -6\)
This tells us that the axis of symmetry of the parabola is \(x =-5\). Since we know that the function has zeros at \(-1\) and \(-11\), we can deduce that the vertex must lie halfway between these two zeros, at\(x = -6\). Therefore, the value of a is:
\(f(-6) = a((-6)+1)(-6) +11) = a(5) (-1) = -5a\)
We also know that the function has a minimum at this point, so we can use this to find the value of a:
\(f(-6) = -5\\-5= -5a\\\\a = 1\)
Therefore, the quadratic function that satisfies these conditions is:
\(f(x) = (x+1) (x+11)\)
We can check that this function has zeros at \(-1\) and \(-11\), and that it has a minimum at\(x =-6\) by finding its vertex:
x-coordinate of vertex = \((-1 +(-11))/2 =-6\)
y-coordinate of vertex =\(f(-6) = (-6+1)(-6+11) = 25\)
Therefore, the minimum point on the graph is \((-6,25)\), which confirms that the function has a minimum at -6.
Which of the following function has zeros at \(-1\) and\(-11\) and a minimum of \(-5\) ?
To know more about graph visit:
https://brainly.com/question/19040584
#SPJ1
CHILCooper, Sha'NiyaScott is constructing a table of values that satisfies the definition of a functionWhich number could be placed in the empty cell so that the table of values satisfies the definition of a function?-1620

Answers
let the equation of function is
y = mx + c
so it will satisfy all the points of the table.
(-8, 3)
3 = m(-8) + c
-8m +c = 3 ....(1)
for (-16, 20)
20 = m(-16)+ c
-16m +c = 20 ......(2)
subtract both the equation
-16m -(-8m) + c - c = 20 - 3
-8m + 0 = 17
m = -17/8
now, multiplied equation 1 by 2
-16m + 2c = 6
- 16m + c = 20
subtract the equation,
-16m -(-16m) + c - 2c = 20 - 6
0 - c = 14
c = -14
so the equation is,
y = (-17/8) x - 14
put y = -16
- 16 = (-17/8)x - 14
-16 + 14 = -17/8x
-2 = -17/8x
x = 16/17
A couple plans to purchase a house. The bank requires a 20% down payment on the $240,000 house. The couple will finance the rest of the cost with a fixed- rate mortgage at 8.5% annual interest with monthly payments over 30 years.
Complete the parts below. Do not round any intermediate computations. Round your final answers to the nearest cent if necessary. If necessary, refer to the list of financial formulas.
(a) Find the required down payment.
(b) Find the amount of the mortgage.
(c) Find the monthly payment.

Answers
(A) The required down payment is $48,000.
(B) The amount of the mortgage is $192,000.
(C) Monthly payment = $192,000 * (0.085/12) * (1 + (0.085/12))^(3012) / (((1 + (0.085/12))^(3012)) - 1)
(a) To find the required down payment, we need to calculate 20% of the house price.
Down payment = 20% of $240,000
Down payment = 0.2 * $240,000
Down payment = $48,000
The required down payment is $48,000.
(b) The amount of the mortgage is equal to the total cost of the house minus the down payment.
Mortgage amount = Total cost of the house - Down payment
Mortgage amount = $240,000 - $48,000
Mortgage amount = $192,000
The amount of the mortgage is $192,000.
(c) To find the monthly payment for the mortgage, we can use the formula for the monthly payment on a fixed-rate mortgage:
Monthly payment = P * r * (1 + r)^n / ((1 + r)^n - 1)
Where:
P = Principal amount (mortgage amount)
r = Monthly interest rate (8.5% annual interest divided by 12 months and converted to a decimal)
n = Total number of monthly payments (30 years multiplied by 12 months)
Monthly payment = $192,000 * (0.085/12) * (1 + (0.085/12))^(3012) / (((1 + (0.085/12))^(3012)) - 1)
Using this formula and performing the calculation will give you the monthly payment amount.
for more questions on down payment
https://brainly.com/question/1698287
#SPJ8
A function is a rule that assigns each ____ exactly one ____.
Answers
Answer:
I found two answers for this question. A function is a rule that assigns to each value of one variable (called the independent variable) exactly one value of another variable (called the dependent variable.) A function is a rule that assigns to each input value a unique output value.
Step-by-step explanation:
I found two answers for this question. A function is a rule that assigns to each value of one variable (called the independent variable) exactly one value of another variable (called the dependent variable.) A function is a rule that assigns to each input value a unique output value.
Use the table in the following table, which lists survey results from high school drivers at least 16 years of age. Assume that subjects are randomly selected from those included in the table.

Answers
Using the hypergeometric distribution, it is found that:
The probability that four randomly selected high school drivers all drove when drinking alcohol is 0.000145.
------------------------------------
The students are chosen from the sample without replacement, which means that the hypergeometric distribution is used to solve this question.In this distribution, the probability of exactly x successes is:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}*C_{N-k,n-x}}{C_{N,n}}\)
In which:
N is the size of the population. n is the size of the sample. k is the total number of desired outcomes.Combination formula:
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
Total of \(709 + 2966 + 179 + 4232 = 8086\) students, thus \(N = 8086\).709 + 179 = 888 drove while drinking, thus \(k = 888\)4 students are selected, thus \(n = 4\).The probability that all four drank is: P(X = 4).\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}*C_{N-k,n-x}}{C_{N,n}}\)
\(P(X = 4) = h(4,8086,4,888) = \frac{C_{888,4}*C_{7198,0}}{C_{8086,4}} = 0.000145\)
Thus, the probability is of 0.000145.
A similar problem is given at https://brainly.com/question/4818951
The height of cylinder B is twice the height of cylinder A the total surface area of cylinder A is 180 Calculate the total surface area of cylinder B
Answers
Main Answer: The total surface area of cylinder B is approximately 476.7 square units.
Supporting Question and Answer:
How is the surface area of a cylinder calculated?
The surface area of a cylinder is the sum of the areas of its curved surface and two circular bases. It can be calculated using the formula:
A = 2πrh + 2π\(r^{2}\)
where "r" is the radius of the circular base, "h" is the height of the cylinder, and π (pi) is a mathematical constant that represents the ratio of the circumference of a circle to its diameter, approximately equal to 3.14159.
The first term, 2πrh, represents the area of the curved surface of the cylinder, while the second term, 2π\(r^{2}\), represents the combined area of the top and bottom circular bases.
Body of the Solution: Let the height and radius of cylinder A be "h" and "r" respectively. Then, the height and radius of cylinder B are "2h" and "R" respectively, since cylinder B has twice the height of cylinder A but the same radius.
The total surface area of a cylinder is given by the formula:
Area = 2πrh + 2π\(r^{2}\)
For cylinder A, we know that the surface area is 180, so we can substitute the values and solve for "r" as follows:
180 = 2πrh + 2π\(r^{2}\)
90 = πrh + π\(r^{2}\)
We can rearrange this equation to solve for r:
r² + rh - 90/π=0
Using the quAdratic formula,we get:
r = (-h ± √((h)² + 4(90/π)))/2
r = -h/2 ± √(h² + 4(90/π))/2
Now we have an expression for r in terms of h . We can use this expression to find the radius of cylinder B, since we know that cylinder B has twice the height of cylinder A.
R = 2r= -h ± √(h² + 4(90/π))
We can use this expression to find the surface area of cylinder B:
Surface area of cylinder B = 2πR² + 2πR(2h)
Surface area of cylinder B= 2π( -h ± √(h² + 4(90/π)))² + 4πh( -h± √(h² + 4(90/π)))
We can use the value we found for 2h using the quadratic formula in the expression to get:
Surface area of cylinder B = 476.7 square units (rounded to one decimal place)
Therefore, the total surface area of cylinder B is approximately 476.7 square units.
Final Answer: Therefore, the total surface area of cylinder B is approximately 476.7 square units.
To learn more about the surface area of a cylinder from the given link
https://brainly.com/question/27440983
#SPJ4
Aviation A plane leaves an airport and flies south at 180 mph.
Later, a second plane leaves the same airport and flies south at
450 mph. If the second plane overtakes the first one in 12 hours,
how much of a head start did the first plane have?
Answers
The first plane had a head start of 432 minutes.
The speed, time and distance of any entity can be related by the following expression as Distance = Speed × Time. The speed of the first plane is 180 mph and the time given is 12 hours whereas the speed of second plane is 450 mph. Now, the distance travelled by plane A in time 12 hours is given by
Distance = Speed × Time
Distance = 180 × 12
Distance = 2160 miles.
The second also flies 2160 miles to overtake the first plane. It does this at a rate of 450 mph. So, the time taken for it to fly will be
Time = Distance/Speed
Time = 2160/450
Time = 4.8 hours
Since, 1 hour = 60 minutes, Therefore, 4.8 hours = 4.8×60 = 288 minutes. Now, since the first plane flies for 12 hours = 12×60 = 720 minutes. So, the head start = 720 minutes - 288 minutes = 432 minutes.
Learn more about Distance at:
brainly.com/question/12356021
#SPJ9
___ hundreds thousands = 30 ten thousands
Answers
3 hundred thousands = 30 ten thousands
Explanations:Note:
Ten thousand in words = 10,000
30 ten thousands = 30 x 10000 = 300, 000
Therefore 3 hundred thousands = 30 ten thousands
Gideon took out an R150 000 loan this morning, to buy a house. The interest rate on a mortgage is 7,35%. The loan is to be repaid in equal monthly payments over 20 years. The first payment is due one month from today. How much of the second payment applies to the principal balance? (Assume that each month is equal to 1/12 of a year.)
Answers
Answer:
Step-by-step explanation:
To solve this problem, we can use the formula for calculating the fixed monthly payment on a mortgage:
P = (r * PV) / (1 - (1 + r)^(-n))
where:
P = fixed monthly payment
r = monthly interest rate (annual interest rate divided by 12)
PV = present value of the loan (loan amount)
n = total number of payments (number of years multiplied by 12)
Using the given values:
r = 0.0735 / 12 = 0.006125
PV = R150,000
n = 20 x 12 = 240
Then we can calculate the monthly payment:
P = (0.006125 * 150000) / (1 - (1 + 0.006125)^(-240)) = R1,181.91
This means that Gideon will have to pay R1,181.91 every month for 20 years to repay his loan.
To determine how much of the second payment applies to the principal balance, we need to calculate the interest and principal amounts of the first payment.
For the first payment, the interest can be calculated as:
interest1 = r * PV = 0.006125 * 150000 = R918.75
This means that the first payment consists of R918.75 in interest and the rest, R1,181.91 - R918.75 = R263.16 is principal.
To find out how much of the second payment applies to the principal balance, we need to subtract the interest and add the calculated principal amount from the first payment to the amount of the second payment:
principal2 = (P - interest1) + principal1 = (1181.91 - 918.75) + 263.16 = R525.32
Therefore, R525.32 of the second payment applies to the principal balance.
I really need this quick A pump releases water at a rate of 10 gallons every 45 days. What is the unit rate in gallons per week? Enter your answer as a mixed number in simplest form in the box.
Answers
Answer:
14/9 or 1.55555555556
Step-by-step explanation:
determine the values of the missing entries. reduce all fractions to the lowest terms
9x-6y= 18

Answers
By evaluating the given linear relation, we conclude that the complete table is:
x: 2, 0, 1, 14/3
y: 0, -3, -3/2, 4
How to determine the values of the missing entries?Here we have the linear relation:
9x - 6y = 18
And we want to complete the given table, to do so, we just need to evaluate the relation in the given values and with that we can find the missing ones.
For example, the first pair has y = 0.
Evaluating that we get:
9x - 6*0 = 18
9x = 18
x = 18/9 = 2
Then we have the pair (2, 0).
The second has x = 0, replacing that we get:
9*0 - 6*y = 18
y = 18/-6 = -3
So we have the pair (0, -3)
The third has x = 1, replacing that:
9*1 - 6y = 18
-6y = 18 - 9 = 9
y = 9/-6 = -3/2
So we have the pair (1, -3/2)
The last value on the table is y = 4, replacing that:
9x - 6*4 = 18
9x - 24 = 18
9x = 18 + 24 = 42
x = 42/9 = 14/3
Then the complete table is:
x: 2, 0, 1, 14/3
y: 0, -3, -3/2, 4
If you want to learn more about linear relations:
https://brainly.com/question/1884491
#SPJ1
10. Using the two formulae, A=B/6.5 + 2.5, C= B/9A, obtain an expression for C in terms of A alone:
Answers
Answer:
43a + c = 13.25
Step-by-step explanation:
A = 9
C = 81
8x5/4 <.>.= 8
can some one please answer this for me please
Answers
>.
hope it helps...!!!!!!

(6-2x) +(15-3x) where x=0.2
Answers
\( \sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}\)
Expression: \(\displaystyle\sf (6-2x) +(15-3x)\)
Substituting \(\displaystyle\sf x=0.2\):
\(\displaystyle\sf (6-2(0.2)) +(15-3(0.2))\)
Simplifying the expression inside the parentheses:
\(\displaystyle\sf (6-0.4) +(15-0.6)\)
\(\displaystyle\sf 5.6 +14.4\)
Calculating the sum:
\(\displaystyle\sf 20\)
Therefore, \(\displaystyle\sf (6-2x) +(15-3x)\) evaluated at \(\displaystyle\sf x=0.2\) is equal to \(\displaystyle\sf 20\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
TIME REMAINING
44:54
The table below shows the number of cars sold each month for 5 months at two dealerships.
Cars Sold
Month
Admiral Autos
Countywide Cars
Jan
4
9
Feb
19
17
Mar
15
14
Apr
10
10
May
17
15
Which statements are supported by the data in the table? Check all that apply.
The mean number of cars sold in a month is the same at both dealerships.
The median number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The range of the number of cars sold is the same for both dealerships.
The data for Admiral Autos shows greater variability.
Answers
The statements supported by the data in the table are:
The mean number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The data for Admiral Autos shows greater variability.
To determine which statements are supported by the data in the table, let's analyze the given information:
The mean number of cars sold in a month is the same at both dealerships.
To calculate the mean, we need to find the average number of cars sold each month at each dealership.
For Admiral Autos:
(4 + 19 + 15 + 10 + 17) / 5 = 65 / 5 = 13
For Countywide Cars:
(9 + 17 + 14 + 10 + 15) / 5 = 65 / 5 = 13
Since both dealerships have an average of 13 cars sold per month, the statement is supported.
The median number of cars sold in a month is the same at both dealerships.
To find the median, we arrange the numbers in ascending order and select the middle value.
For Admiral Autos: 4, 10, 15, 17, 19
Median = 15
For Countywide Cars: 9, 10, 14, 15, 17
Median = 14
Since the medians are different (15 for Admiral Autos and 14 for Countywide Cars), the statement is not supported.
The total number of cars sold is the same at both dealerships.
To find the total number of cars sold, we sum up the values for each dealership.
For Admiral Autos: 4 + 19 + 15 + 10 + 17 = 65
For Countywide Cars: 9 + 17 + 14 + 10 + 15 = 65
Since both dealerships sold a total of 65 cars, the statement is supported.
The range of the number of cars sold is the same for both dealerships.
The range is determined by subtracting the lowest value from the highest value.
For Admiral Autos: 19 - 4 = 15
For Countywide Cars: 17 - 9 = 8
Since the ranges are different (15 for Admiral Autos and 8 for Countywide Cars), the statement is not supported.
The data for Admiral Autos shows greater variability.
To determine the variability, we can look at the range or consider the differences between each data point and the mean.
As we saw earlier, the range for Admiral Autos is 15, while for Countywide Cars, it is 8. Additionally, the data points for Admiral Autos are more spread out, with larger differences from the mean compared to Countywide Cars. Therefore, the statement is supported.
Based on the analysis, the statements supported by the data are:
The mean number of cars sold in a month is the same at both dealerships.
The total number of cars sold is the same at both dealerships.
The data for Admiral Autos shows greater variability.
for such more question on mean
https://brainly.com/question/14532771
#SPJ8
3.
A Ferris Wheel has a circumference of 78.5 feet. Which expression can be used to find the
radius of the Ferris Wheel?
Please help

Answers
Answer:
G. 78.5 / π
{ i hope this helps :) i'm sorry if its wrong }
Freemont run club surveyed a random sample of 30 of their members about their running habits
Answers
The reasonable estimate would be 25
How to solve for the estimateWe have to solve this using the rule of 3
9 out of 30 members said that they run more than 5 days a week.
We will form the equations
when 9 ran = 30 menbers
when n ran = 84 members
we will then cross multiply
84 x 9 = 30 x n
n = 25.2
When we round this, the reasonable estimate would be 25
Read miore on survey here:https://brainly.com/question/25257437
#SPJ1
Complete question
Freemont Run Club surveyed a random sample of 30 of their members about their running habits. Of the members surveyed, 9 said that they run more than 5 days a week.
There are 84 Freemont Run Club members.
Based on the data, what is the most reasonable estimate for the number of Freemont Run Club members who run more than 5 days a week?
Solve the equation. −2=67p
Answers
Answer:
p = -2/67
Step-by-step explanation:
We divide 67 on both sides.
-2 / 67 = -2/67
67p / 67 = p
We got p = -2/67
Hope this helps.
Solution for the attached question below

Answers
The solution to the question is 265.
What is the logarithm of a number?Logarithm of a number A is the exponent or power or index n, a given number called the base B would be raised to give the number A.
So n is the logarithm of A to base B.
Analysis:
log 2( log2(x-9)) = 3
log2(x-9) = \(2^{3}\)
log2(x-9) = 8
x-9 = \(2^{8}\)
x-9 = 256
x = 256 + 9
x = 265
Learn more about logarithm: brainly.com/question/25710806
#SPJ1
solve and graph the inequality 3x < 13

Answers
The solution of the inequality 3x < 13 is x < 4.33.
None of the given option is correct.
What is an inequality?In mathematics, "inequality" refers to a relationship between two expressions or values that are not equal to each other. To solve the inequality, you may multiply or divide each side by the same positive number, add the same amount to each side, take the same amount away from each side, and more. You must flip the inequality sign if you multiply or divide either side by a negative number.
Given:
An inequality,
3x < 13.
Simplifying,
x < 4.33
The graph is given in the attached image.
Therefore, the solution is x < 4.33.
To learn more about the inequality;
brainly.com/question/28823603
#SPJ1

Use a graphing utility to approximate the solutions (to three decimal places) of the equation in the interval [0, 2). (Enter your answers as a comma-separated list.)
7 csc^2 x + 3.5 cot x − 35 = 0
Answers
Answer:
Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is 2π. In other words, every 2π units, the y-values repeat. If we need to find all possible solutions, then we must add 2πk, where k is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is 2π:
sinθ=sin(θ±2kπ)
There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.
Step-by-step explanation:
Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval.
The perimeter and area of a rectangle are 22 cm
and 30 cm² respectively. Find the length and
breadth of the rectangle
Answers
The perimeter and area of a rectangle are (5,6) and (6,5).
The perimeter method for a rectangle states that P = (L + W) × 2, where P represents perimeter, L represents length, and W represents width. when you are given the size of a square form, you may simply plug within the values of L and W into the formula that allows you to clear up for the fringe.
A perimeter is a closed course that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional period. The perimeter of a circle or an ellipse is known as its circumference. Calculating the perimeter has several practical programs.
The perimeter P of a rectangle is given by means of the method, P=2l+2w, in which l is the period and w is the width of the rectangle. The place A of a rectangle is given with the aid of the components, A=lw, wherein l is the length and w is the width.
The perimeter of the rectangle:
P=2l+2w=22
divide 2 into both sides
l+w=11 -------------> (1)
w=11-l
Area of the rectangle:
l*w=30
l(11-l)=30
11l-l^2-30=0
l^2-11l+30=0
By factor method,
(l-5)(l-6)=0
l=5,6.
Substitute this value in w,
l=5 implies w=6
l=6 implies w=5
There we have two solutions.
The length and breadth of the rectangle is
(5,6) and (6,5).
Learn more about perimeter here https://brainly.com/question/397857
#SPJ9
The occupancy of the room must be less than 437 people
a) p 437
c) p ≤ 437
d) p ≥ 437
Answers
A cubic root function has a domain of x≥−3 and a range of y≥−1. What is the range of its inverse?
Answers
In general, if the range of a function is y≥−1, its inverse has a domain of y≥−1. So, the range of the inverse of the cubic root function is y≥−1.
How do we know this?The range of a cubic root function becomes the domain of a cube function and vice versa since a cubic root function is an inverse function of a cube function. Therefore, the cube function's range is x3 if the cubic root function's domain is x3.
A function's inverse typically has a domain of y1 if its range is y1. Therefore, y1 is the domain of the inverse of the cubic root function.
Describe a function.
A function is a mathematical relationship between a domain—a set of inputs—and a range—a set of outputs. Each input in the domain is given a distinct output, known as the function value, by a function. An equation or graph can be used to depict the function value.
A function is typically represented symbolically by an equation that describes the relationship between the inputs and outputs and a letter, like f or g, as well as the letter. For instance, the equation of a function that accepts a value of x as input and produces its square is f(x) = x2.
Learn more about Functions here
https://brainly.com/question/17043948
#SPJ1
What is the constant up a proportionally in a equation y=x/g
Answers
Answer:
Step-by-step explanation:
\(y=(\frac{1}{g} )x\)
Constant up a proportionally is \(\frac{1}{g}\).
A 6 ft tall person walks away from a 10 ft lamppost at a constant rate of 3 ft/s. What is the rate (in ft/s) that the tip of the shadow moves away from the pole when the person is 15 ft away from the pole
Answers
Answer:
12.5 ft/s
Explanation:
Height of person = 6 ft
height of lamp post = 10 ft
According to the question,
dx / dt = 5 ft/s
Let the rate of tip of the shadow moves away is dy/dt.
According to the diagram
10 / y = 6 / (y - x)
10 y - 10 x = 6 y
y = 2.5 x
Differentiate both sides with respect to t.
dy / dt = 2.5 dx / dt
dy / dt = 2.5 (5) = 12.5 ft /s
8. Write a paragraph proof.
Proof Given: In a plane, a is perpendicular to b, b id perpendicular to c, and c || d.
Prove: a || d
Answers
To prove that line segment a is parallel to line segment d, based on the given information, we can utilize the properties of perpendicular and parallel lines.
Given that a is perpendicular to b and b is perpendicular to c, we know that angles formed between a and b, as well as between b and c, are right angles. Let's denote these angles as ∠1 and ∠2, respectively.
Now, since c is parallel to d, we can conclude that the corresponding angles ∠2 and ∠3, formed between c and d, are congruent.Considering the fact that ∠2 is a right angle, it can be inferred that ∠3 is also a right angle.
By transitivity, if ∠1 is a right angle and ∠3 is a right angle, then ∠1 and ∠3 are congruent.Since corresponding angles are congruent, and ∠1 and ∠3 are congruent, we can deduce that line segment a is parallel to line segment d.
Thus, we have successfully proven that a is parallel to d based on the given information and the properties of perpendicular and parallel lines.
For more such questions on line segment
https://brainly.com/question/30756145
#SPJ8
I need help. Please check this problem for accuracy I turn it in tomorrow.
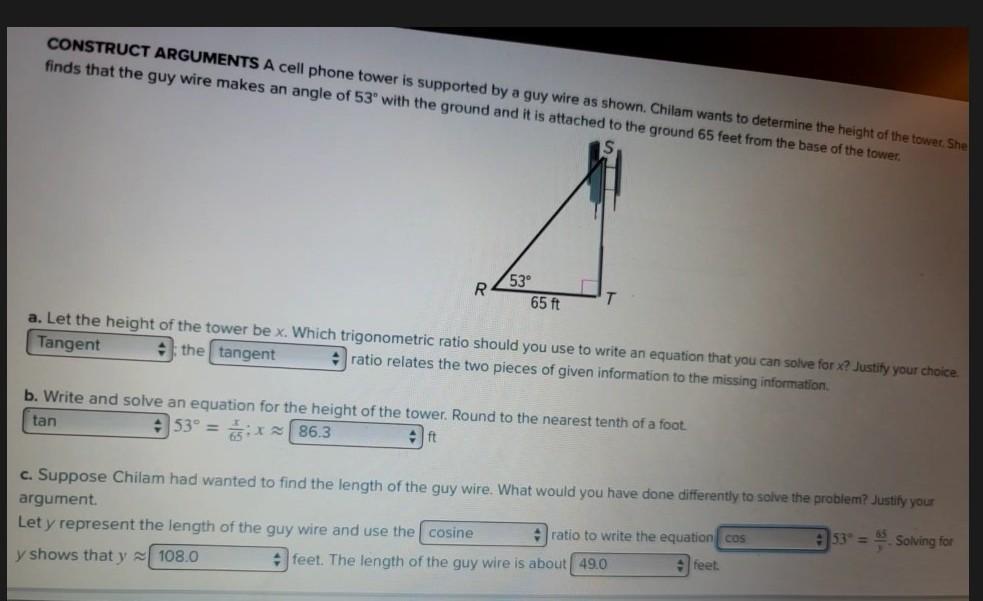
Answers
Answer:
you are 100% correct (^_^)
Step-by-step explanation:
Please view image & please help.. thank you appreciate it:)

Answers
is it -12 cause, I've not done these in a long time but if you do 6 - (-12) you get 18 and 18 is bigger that 16. I hope it's right but I'm unsure.
