Answers
Answer:
8a. $432
8b. about 36 2/3 hours
9. %17.50 per article
10. $338.4 after 3 weeks
Step-by-step explanation:
Related Questions
(WILL GIVE BRAINLIEST)
The points (2, -4), (x,y), A and B all lie on the line in the applet below. Find an equation relating x and y

Answers
Answer:
y=3/4x-5.5 this should be your answer
Step-by-step explanation:
sorry of im wrong
have a wonderfull day!
What is the Scale used at Mt. Rushmore if George Washington's head was 8 inches long where Mt. Rushmore measures 60 feet?
1 inch=____feet
PLEASE BE ACCURATE!!! Thank you!:)
Answers

Express your answer in scientific notation\(0.00045 - 2.5 \times 10 {}^{ - 5} \)
Answers
The given expression is
\(0.00045-2.5\times10^{-5}\)First, we express the first number in scientific notation. We have to make sure that both scientific notations have the same exponent.
\(45\times10^{-5}-2.5\times10^{-5}\)Then, we subtract the coefficients.
\((45-2.5)\times10^{-5}=42.5\times10^{-5}=4.25\times10^{-4}\)Therefore, the answer is\(4.25\times10^{-4}\)I tried many times to solve this question: Joy makes 6,5 litres soup correct to the nearest 0.5 litres. She serves the soup in 280ml portions correct to the nearest 10ml. 22 people order this soup. Does joy definitely has enough soup to serve the 22 people. show how you decide Your final line must be written as joy definitely does have enough soup or joy may not have enough soup. If you can please explain it if not just give the answer.
Answers
Joy makes 6.5 litres soup correct to the nearest 0.5 litres. She serves the soup in 280ml portions correct to the nearest 10ml. 22 people order this soup. Does joy definitely has enough soup to serve the 22 people.
Answer:
Yes, Joy definitely does has enough soup
Step-by-step explanation:
From the question, we know,
Joy make 6.5 litres of soup
Serves it in 280ml portions
Step 1
We convert the portions to liters
1 ml = 0.001 litre
280 ml
= 280ml × 0.001 litre/1 ml
= 0.28litre
Step 2
We divide 6.5 liters by 0.28 to find out how many people can be served
= 6.5 ÷ 0.28
= 23.2142857143 people
We can see that 6.5 liters soup can serve 23 people approximately.
Therefore, Yes, Joy definitely does has enough soup to serve 22 people
write an equivalent expression by combining like terms (3/5y+4)+(1/5y-1)
Answers
You just add the like terms
determine if a line can have a constant rate and not be proportional write and argument to defend your response
Answers
By definition two quantities are proportional of each other if it can be express like:
\(y=kx\)where k is the constant of proportionality.
Now, by definition a line is a set of points that have the same rate of change between them, no matter which points we take.
Thus we can argue that a line always have a constant rate but they don't necessarily represent proportional quantities.
Can someone please help me?

Answers
Answer: I think a
Step-by-step explanation:
which of the following statements about the upper and lower control limits of a control chart is true? group of answer choices the upper control limit of an x-bar chart does not depend on the average range r-bar. the lower control limit of a p chart will always be a negative value. the upper and lower control limits for a p chart depend on the sample size. the upper and lower control limits of an r chart are always the same distance from r-bar.
Answers
The correct statement among the provided choices is: the upper and lower control limits for a p chart depend on the sample size.
A p-chart is used to monitor the proportion of defective items in a sample. The control limits depend on the sample size, as larger sample sizes typically result in smaller control limits. The other statements provided are not true.
The upper control limit of an x-bar chart does depend on the average range R-bar, the lower control limit of a p chart may not always be a negative value, and the upper and lower control limits of an R chart are not always the same distance from R-bar.
You can learn more about p chart at: brainly.com/question/31143613
#SPJ11
Absolute value equation with solution -3
Answers
Answer:
m=-3/5
Step-by-step explanation:
What pattern would appear in a graph of the equation Y = 4X - 1 (or Y = -1 + 4X)?
A. A line that slopes gradually up to the right
B. A line that slopes gradually down to the right
C. A line that slopes steeply up to the right
D. A line that slopes steeply down to the right
Answers
The graph of the equation Y = 4X - 1 (or Y = -1 + 4X) represents (A) a line that slopes gradually up to the right.
Determine the form of a linear equation?The equation Y = 4X - 1 (or Y = -1 + 4X) is in the form of a linear equation, where the coefficient of X is 4. This indicates that for every increase of 1 in the X-coordinate, the Y-coordinate will increase by 4. This results in a positive slope.
When graphed on a Cartesian plane, the line represented by this equation will slope gradually up to the right. The slope of 4 means that the line rises 4 units for every 1 unit it moves to the right. This creates a steady and consistent upward trend as X increases.
Therefore, (A) the pattern observed in the graph is a line that slopes gradually up to the right.
To know more about Cartesian plane, refer here:
https://brainly.com/question/27927590#
#SPJ4
PLEASEEEE HELPPPPPP ME

Answers
Answer:
k
Step-by-step explanation:
find the value of for which the area enclosed by the curves =−2 and =2− is equal to 128.
Answers
At the value of c = 21 (approx) for which the area enclosed by the curves y = c - x^2 and y = x^2 - c is equal to 128.
The curves are y = c - x^2 and y = x^2 - c
The area enclosed by these curves is 128.
We must determine the x-coordinates of the places of intersection in order to determine the bounds of integration:
c - x^2 = x^2 - c
Subtract c on both side, we get
-x^2 = x^2 - 2c
Subtract x^2 on both side, we get
-2x^2 = -2c
Divide by -2 on both side, we get
x^2 = c
Taking square root on both side, we get
x = ±√c
The between the curve is given by
\(\int\limits^{\sqrt{c}}_{-\sqrt{c}}{[(c-x^2)-(x^2-c)]} \, dx\) = 128
Simplify
\(\int\limits^{\sqrt{c}}_{-\sqrt{c}}{(c-x^2-x^2+c)} \, dx\) = 128
\(\int\limits^{\sqrt{c}}_{-\sqrt{c}}{(2c-2x^2)} \, dx\) = 128
\(2\int\limits^{\sqrt{c}}_{-\sqrt{c}}{(c-x^2)} \, dx\) = 128
Now integrating with respect to x
\(2\left(cx-\frac{x^3}{3}\right)^{\sqrt{c}}_{-\sqrt{c}}\) = 128
\(2\left[\left(c(\sqrt{c})-\frac{(\sqrt{c})^3}{3}\right)-\left(c(-\sqrt{c})-\frac{(-\sqrt{c})^3}{3}\right)\right]\) = 128
\(2\left[\left(c(\sqrt{c})-\frac{(\sqrt{c})^3}{3}\right)-\left(-c\sqrt{c}+\frac{(\sqrt{c})^3}{3}\right)\right]\) = 128
\(2\left[c\sqrt{c}-\frac{(\sqrt{c})^3}{3}-c\sqrt{c}-\frac{(\sqrt{c})^3}{3}\right]\) = 128
\(2\left[-\frac{2(\sqrt{c})^3}{3}\right]\) = 128
\(-\frac{4}{3}(\sqrt{c})^3\) = 128
\(-\frac{4}{3}(c\sqrt{c})\) = 128
Multiply by -3/4 on both side, we get
c(√c) = -96
Square on both side, we get
c^2(c) = 9216
c^3 = 9216
Taking cube root on both side, we get
c = 20.97
c = 21 (approx)
To learn more about area enclosed by curves link is here
brainly.com/question/30174664
#SPJ4
The complete question is:
Find the value of c for which the area enclosed by the curves y = c - x^2 and y = x^2 - c is equal to 128.
series with 12 terms,a1=3 and a12=25
Answers
The 12 terms of the series will be -
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25
What is the formula to calculate the nth term of an Arithmetic Sequence ?The formula to calculate the nth term of an Arithmetic Sequence is -
a(n) = a + (n - 1)d
a - first term of A.P.
d - Common difference of A.P.
n - position of term
We have -
a[1] = 3
a[12] = 25
Then, using the formula to calculate the nth term, we get -
a(n) = a + (n - 1)d
a[1] = 3
AND
a(12) = 3 + 11 x d
25 = 3 + 11d
22 = 11d
d = 2
So, the terms of the series will be -
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25
Hence, the 12 terms of the series will be -
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25
To solve more questions on Arithmetic Sequences, visit the link below-
brainly.com/question/19828148
#SPJ1
the 3 conditions for sampling distributions must be met in order to calculate p-hat. group of answer choices true false
Answers
The correct answer is False because, If the sample size is large enough (n greater than or equal to 30) the sampling distribution is approximately normal regardless of the shape of the population.
The sample fraction, often called the "p-hat", is the ratio of the number of sample successes to the size of the sample. The standard deviation of (p) decreases as the sample size n increases. This is because n is included in the denominator of the standard deviation formula. That is, (p has) has fewer variables for larger samples. The P-hat (must be a lowercase p with a caret (^) circumflex) indicates the percentage of the sample (this is the x-bar, the average of the samples).
A p-hat (proportion) sampling distribution is a collection of equal-sized repeated sample proportions drawn from the same population to represent it. According to the central limit theorem, the sampling distribution of p-hat is approximately normally distributed for large sample sizes.
To know furthermore about P-Hat at
https://brainly.com/question/12360461
#SPJ4
What is the solution of the system graphed below?
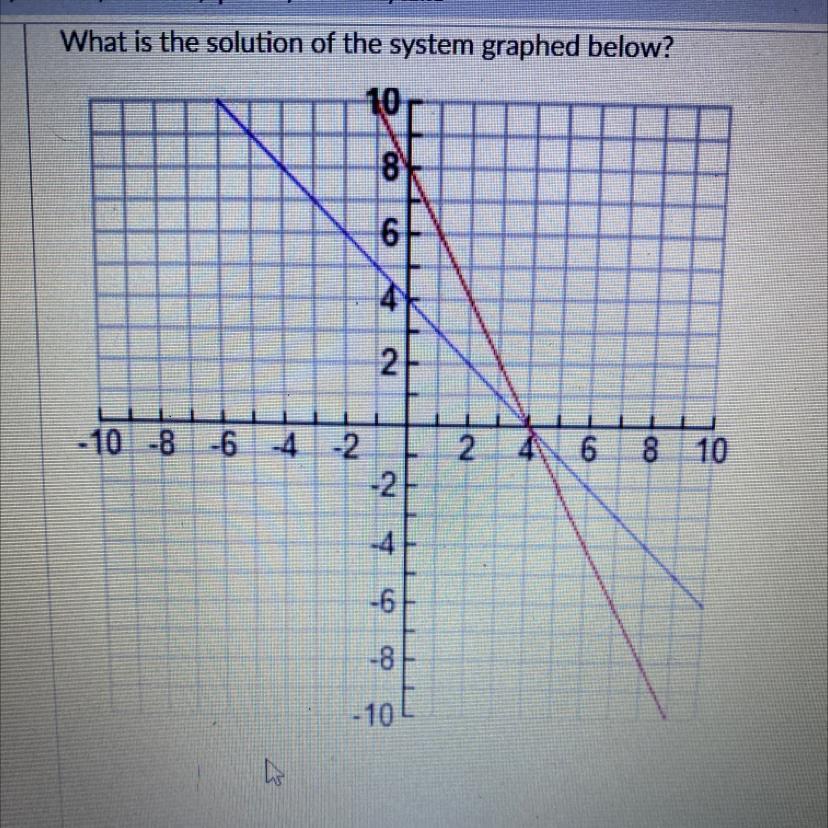
Answers
Answer:
4
Step-by-step explanation:
Mariah is drawing a picture on a square sheet of paper. The paper has an
area of 49 square inches. What is its perimeter?
Show your work.
Answers
Answer:
28 inches.
Step-by-step explanation:
The side length of the square can be found by taking the square root of the area, which is 7 inches.
The perimeter of a square is simply 4 times the length of one of its sides, so the perimeter of this square paper is:
4 x 7 inches = 28 inches
Solve the following systems of equations algebraically. Then graph each system to confirm your solution.
a. x+y=3
x=3y−5
b. x−y=−5
y=−2x−4
Answers
Answer:
Step-by-step explanation:
a.
To solve this system of equations, we can substitute the value of x from the second equation into the first equation:
x = 3y - 5
x + y = 3
Substituting x:
3y - 5 + y = 3
4y - 5 = 3
4y = 8
y = 2
Now, we can substitute y = 2 back into either equation to find x:
x + 2 = 3
x = 1
So the solution to the system of equations is (x, y) = (1, 2).
To confirm this solution, we can graph both equations on the same coordinate plane and see where they intersect:
x + y = 3 is a line with a y-intercept of 3 and a slope of -1.
x = 3y - 5 is a line with a y-intercept of -5/3 and a slope of 3.
Graphing these lines, we can see that they intersect at the point (1, 2), confirming our solution.
b.
To solve this system of equations, we can substitute the value of y from the second equation into the first equation:
y = -2x - 4
x - y = -5
Substituting y:
x - (-2x - 4) = -5
x + 2x + 4 = -5
3x = -9
x = -3
Now, we can substitute x = -3 back into either equation to find y:
y = -2(-3) - 4
y = 2
So the solution to the system of equations is (x, y) = (-3, 2).
To confirm this solution, we can graph both equations on the same coordinate plane and see where they intersect:
y = -2x - 4 is a line with a y-intercept of -4 and a slope of -2.
x - y = -5 is a line with a y-intercept of 5 and a slope of 1.
Graphing these lines, we can see that they intersect at the point (-3, 2), confirming our solution.
Help will mark brainiest

Answers
So first Isolate the variable by dividing each side by factors that don't contain the variable.
y= 3x/2 + 3
Hope this helps!
Here is the equation given:
\(-6x=12-4y\)
In the equation, you're looking for y. That means you need to move anything with the variable y to the other side.
In this equation, you have 12-4y. To move 12 to the other side, you will need to subtract 12 on both sides. This is because when a variable or integer is moved, the sign changes. The 12 was originally positive, but when moving it, it will become -12, which is why it was subtracted.
\(-6x-12=12-4y-12 \\-6x-12=-4y\)
Remember you're looking for y alone. y is currently -4y. To remove the -4 that is being multiplied by y, you will need to do the opposite of it, which is divide by -4. Divide both sides by -4:
\(\frac{-6x-12}{-4} =\frac{-4y}{-4}\)
When a negative number is multiplied by another negative number, the sign becomes positive. On the left side, you have -6x-12, which is being divided by -4. When you divide, \(\frac{-6x}{-4}\) becomes \(\frac{6}{4}\).
\(\frac{-6x-12}{-4} =\frac{-4y}{-4}\\\frac{6}{4}x+3=y\)
\(\frac{6}{4}\) cans till be simplified. The greatest common factor of 6 and 4 is 2, so divide the fraction by 2.
\(\frac{6 \div 2}{4 \div 2} =\frac{3}{2}\)
That means \(\frac{3}{2}x+3=y\)
The answer you are looking is \(\bf \frac{3}{2}\).
Find the distance between each pair of points (-4,6) and (3,-7)
Answers
Answer:
Here is your answer . Hope this helps you.

Answer:
\(\boxed {\boxed {\sf \sqrt{218} \ or \ 14.76}}\)
Step-by-step explanation:
The formula for calculating the distance between 2 points is:
\(d= \sqrt{(x_2-x_1)^2 +(y_2-y_1)^2\)
In this formula, (x₁, y₁) and (x₂, y₂) are the 2 points. The 2 points we are given are (-4, 6) and (3, -7). If we match the value with the corresponding variable we see that:
x₁ = -4 y₁ = 6 x₂ = 3 y₂ = -7Substitute the values into the formula.
\(d= \sqrt{(3 - -4)^2 + (-7-6)^2\)
Solve inside the parentheses.
(3--4) = (3+4) = 7 (-7-6) = -13\(d=\sqrt {(7)^2 + (-13)^2\)
Solve the exponents.
(7)²= 7*7 = 49 (-13)² = -13 * -13 = 169\(d= \sqrt{ (49)+(169)\)
Add.
\(d= \sqrt{218}\)
\(d=14.76482306\)
If we round to the nearest hundredth place, the 4 in the thousandth place tells us to leave the 6.
\(d \approx 14.76\)
The distance between the points (-4, 6) and (3, -7) is √218 or approximately 14.76.
What is the answer? How do I solve this?

Answers
You solve it using your brain.
The Row of peas measured 1 1/6 yards and the row of lettuce measured 4 feet long how many inches long was the row of peas and the row of lettuce together?
Answers
The row of peas and the row of lettuce together are 90 inches long.
How to change yard to inches?The length of the row of peas is \(1\ \frac{1}{6}\ \text{yards}\) which can be converted to inches by multiplying it with 36 (1 yard = 36 inches).
So, the length of the row of peas is:
\($\begin{equation*}1\frac{6}{1} \text{ yards} = \left(1+\frac{1}{6}\right) \text{ yards} = \frac{7}{6} \text{ yards} = \frac{7}{6} \times 36 \text{ inches} = 42 \text{ inches}\end{equation*}\)
The length of the row of lettuce is 4 feet which can be converted to inches by multiplying it with 12 (1 foot = 12 inches).
So, the length of the row of lettuce is:
4 feet = 4 × 12 inches = 48 inches
Therefore, the total length of the row of peas and lettuce together is:
42 inches+48 inches=90 inches
Hence, the row of peas and the row of lettuce together are 90 inches long.
To know more about Mixed fraction visit:
brainly.com/question/29264210
#SPJ1
Find the length of the known side

Answers
7. If n # 81, find the critical values x 2/l and x 2/h for a confidence level of 99%, (1 point)
59.196, 128,299
53.540, 112.329
64,278,96,578
51.172, 116,321
Answers
Answer: 51.172, 116.321
what is the slope of the line?

Answers
Answer:
Slope = (-3/2)
Step-by-step explanation:
Slope(m) = (Y2 - Y1) / (X2 - X1)
= (0-3) / (2-0)
= (-3/2) Is the ans....
This year, the girl scouts sold 2 more than four times as boxes of cookies as they did last year. This year they sold 402 boxes.
How many boxes did they sell last year?
Answers
Answer:
100
Step-by-step explanation:
they sold 2 more that 4 times as many, so subtract two
402-2=400
then divide by four
400/4=100
Hope this helps!
PLEASE HELP THIS IS THE OTHER PART ALSO DUE IN LIKE 3 MINUTES
Write in the coordinates of the points marked
The letters are in on picture


Answers
Answer:
a= 4,3
b=1,2
c=-3,4
d=-1,2
e= -2,-1
f= -4,-3
g=1,-2
h=4,-1
k=-3,0
In September, 8 out of 10 days were rainy. How many total days in September were rainy? I Will Give You 15 Points
Answers
Answer:
8 days where raining out of 10. means 2 days where not raning so 8 days where raning and 2 was not.
Let
P(Xy, X2, X3) = f(X)g (X2, X3) be a positive distribution. List all
the independencies
associated
with this distribution, ie the elements in /(P) with justification.
Draw a Markov network to repr
Answers
In this network, there are no direct connections between X2 and X3, indicating their independence. X is connected to both X2 and X3, but they are not connected to each other, indicating their conditional independence given X.
To determine the independencies associated with the distribution P(X, X2, X3) = f(X)g(X2, X3), we can examine the conditional independence relationships implied by the distribution. Here are the independencies:
1. X is independent of X2 given X3: X ⊥ X2 | X3
Justification: Since X is independent of X2 given X3, the distribution can be factorized as P(X, X2, X3) = P(X | X3)P(X2, X3). This implies that X and X2 are conditionally independent given X3.
2. X is independent of X3 given X2: X ⊥ X3 | X2
Justification: Similarly, if X is independent of X3 given X2, the distribution can be factorized as P(X, X2, X3) = P(X, X2)P(X3 | X2). This implies that X and X3 are conditionally independent given X2.
3. X2 is independent of X3: X2 ⊥ X3
Justification: If X2 is independent of X3, the distribution can be factorized as P(X, X2, X3) = P(X)P(X2, X3). This implies that X2 and X3 are marginally independent.
These independencies can be represented using a Markov network or Bayesian network as follows:
X ----- X2
\ /
\ /
X3
In this network, there are no direct connections between X2 and X3, indicating their independence. X is connected to both X2 and X3, but they are not connected to each other, indicating their conditional independence given X.
Please note that the specific form of the functions f(X) and g(X2, X3) would determine the exact relationships and independencies in the distribution, but based on the given information, these are the independencies we can deduce.
Visit here to learn more about distribution brainly.com/question/29664850
#SPJ11
A cash card has a starting value of $25. If the card is not used within the first year of its purchase, the value on the card begins to decrease by $2.50 per month.
The relationship between the number of months after the first year and the amount remaining on the card is continuous or discrete
.
The independent variable is the amount remaining on the card or number of months after the first year
.
The dependent variable is the amount remaining on the card or number of months after the first year
.
.
Answers
The relationship between the number of months after the first year and the amount remaining on the card is y = - 2.5 x + 25.
The independent variable is number of months after the first year.
The dependent variable is the amount remaining on the card.
How to find the relationship ?The relationship between the number of months after the first year would be:
Amount remaining = Starting value - ( Amount decreasing by x Number of months )
y = 25 - ( 2. 50 x )
This can be written as:
y = - 2. 50 x + 25
The independent variable is the x value and as shown above, this is the number of months after the first year. This then means that the dependent variable would the amount remaining.
Find out more independent variable at https://brainly.com/question/82796
#SPJ1
Find the value of x. Round your answer to the nearest tenth

Answers
\(x=13.8\)
Step-by-step explanation:
Since the triangle is right use the tangent ratio to solve for x\(tan41^o=\frac{opposite}{adjacent}=\frac{12}{x}\)
Multiply both sides by \(x\)x × \(tan41^o=12\) ( divide both sides by \(tan41^o\) )
x = ≈ ( nearest tenth )
