Please Help MEEEE!!!! 50 points
Wanda has $640 in her checking account. She pays her landlord $75 per week for rent.
Which function best models the linear relationship?
Group of answer choices
y = 640x + 75
y = -75x + 640
y = -75x - 640
y = 75x + 640
Answers
Answer:
y = -75x + 640
Step-by-step explanation:
y = 640 - 75x ....................where y is how much money she has left and x the number of weeks
Answer:
B
Step-by-step explanation:
I got it right on my test
Related Questions
HELP ME PLEASE !!!!!!

Answers
C(x)= 50.41
for the minute multiplying 9×50= 400 minute
Find the circumference.
Use 3.14 for tı.
-
r = 6 ft
C = [?] ft
C=rd
![Find the circumference.Use 3.14 for t.-r = 6 ftC = [?] ftC=rd](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/sgJVQydkc6NtVw10SBgr4sKXWK78Qzfg.png)
Answers
Answer:
37.69911184
Step-by-step explanation:
because circumference is equal to pi multiplied by diameter, you will not get the circumference with the radius times pi. in order to get the diameter, you multiply the radius by 2, because the diameter is the length across the circle. So the diameter of this circle is equal to 12. so simply multiply that number by pi (3.14) and there is your answer. Hope i helped.
A pie company randomly surveys 60 customers to determine which type of pie they would purchase.
The results of the survey are shown.
Favorite Type of Pie
Peach
25%
Apple
331%
Other
20%
Cherry
The company expects to sell 65 cherry pies in March.
Based on the survey results, how many whole peach pies should the company expect to sell in March?
Answers
Answer:
Explained below.
Step-by-step explanation:
Construct the frequency distribution from the percentage distribution as follows:
Favorite Type of Pie Percentage Frequency
Peach 25% 25% of 60 = 15
Apple 31% 31% of 60 = 18.6
Other 20% 20% of 60 = 12
Cherry 24% 24% of 60 = 14.4
TOTAL 100% 60
It is provided that the company expects to sell 65 cherry pies in March.
The total number of people buying pies is:
\(\#\text{People buying Cherry pies}=\#\text{People buying pies}\times 0.24\\\\\#\text{People buying pies}=\frac{65}{0.24}\\\\\#\text{People buying pies}=270.833\)
Now compute the number of peach pies should the company expect to sell in March as follows:
\(\#\text{Peach pies expected to be sold}=270.833\times 0.25 =67.7\approx 68\)
A graph titled Population of Ohio has years on the x-axis and population (millions) on the y-axis. Points are at (1930, 7), (1950, 8), (1970, 10.5), (1990, 10.8), (2010, 11.8).
What relationship between the population of Ohio and the number of years is displayed in the scatterplot ?
As the number of years increased, the population increased.
As the number of years increased, the population stayed the same.
As the number of years increased, the population decreased.
As the number of years decreased, the population decreased.
Answers
Answer
A.) As the number of years increased, the population increased.
And insurance agent receives 15% of the cost of each insurance policy she sells how much does the agent receive for a policy thst cost $300
Answers
In this question there are several important information's provided. Using these information's it is easy to get the answer to the question asked. Firstly it is already informed that the insurance agent gets a commission of 15% of the policy price for every policy sold. The agent sells a policy of $300.
Now we can write the equation as:
15% of $300 = [(15/100) * 300] dollars
= ( 15 * 3) dollars
= 45 dollars
So the agent gets a commission of $45 for selling a policy worth $300
Find the general solution of the following PDE: \[ u_{x x}-2 u_{x y}-3 u_{y y}=0 \]
Answers
We need to find the general solution of the above PDE. Let's solve the above PDE by the method of characteristic. Let us first solve the PDE by using the method of characteristics.
The method of characteristics is a well-known method that provides a solution to the first-order partial differential equations. To use this method, we first need to find the characteristic curves of the given PDE. Thus, the characteristic curves are given by $x = t + c_1$.
Now, we need to eliminate $t$ from the above equations in order to obtain the general solution. By eliminating $t$, we get the general solution as:$$u(x,y) = f(2x - 3y) + 3(x - 2y)$$ where $f$ is an arbitrary function of one variable. Hence, the general solution of the PDE $u_{xx} - 2u_{xy} - 3u_{yy} = 0$ is given by the above equation. Thus, the main answer to the given question is $u(x,y) = f(2x - 3y) + 3(x - 2y)$. In order to find the general solution of the PDE $u_{xx} - 2u_{xy} - 3u_{yy} = 0$, we first used the method of characteristics. The method of characteristics is a well-known method that provides a solution to the first-order partial differential equations.
To know more about solution visit:
https://brainly.com/question/1616939
#SPJ11
Find the value of x.

Answers
Answer:
x = 132°
Step-by-step explanation:
sum of total exterior angles = 360°
x + 147° + 81° = 360°
x + 228° = 360°
x = 360° - 228°
x = 132°
Andrew rode his bike at a constant speed.He rode 1mile in 5 minutes.
Which of these equations represents the amount of time1(in minute) that it takes him to ride a distance of d miles?
A. t=5d B. t=1/5 C. t=d+4 D. t=d-4
Answers
Answer:
3
Step-by-step explanation
The answer is three because if you did the tree method you will have the same exact answer
B. t=1/5 because you divide 1 mile by 5 minutes and you get 0.2
5. A ball is thrown into the air from the edge of a 48-foot-high cliff so that it eventually lands
on the ground. The graph below shows the height, y, of the ball from the ground after x
seconds
For which interval is the ball's height always decreasing?
A. 0
B. 0
C. 2.5
D.) 2
Answers
Please Help
2 and 23/75 as a percentage
Answers
Answer:230.666667%
Step-by-step explanation: Convert the fraction to a decimal: Divide the numerator by the denominator
Add this decimal number to the whole number part of the mixed number
A mixed number is a whole number plus a fraction. To find the decimal form of a fraction just divide the numerator by the denominator using a calculator or long division. Then add the decimal number to the whole number.
What is 2 9/12×6=.........
Answers
Step-by-step explanation:
2 9/12×6=(2×12+9)/12×6=33×6/12=33/2=16.5is answer
12x6=33x6/12=33/2=16.5
-5 + 3g + (-3) - 8g = -18
Answers
Answer:
the answer is g=2
Step-by-step explanation:
hope this helps!!!

Convert these units of length.
1. 108 in. =
ft.
2.
3.
12 ft. =
1 yd.:
yd.
in. isqe sd
Answers
After converting all the given units of length into meters we get,
\(108 in = 2.7432 m\\108 ft = 32.9184 m\\12 ft = 3.6576m\\1 yd= 0.9144m\)
As per the question statement, we are supposed to convert these given units of length into meters i.e., 108 inches, 108 feet, 12 feet, 1 yard.
We know
\(1 foot = 12 inches\)
\(1 inch = 2.54 cm\\\)
\(12 inches = 2.54*12=30.48 cm\\1 cm = 0.01 m \\30.48 cm = 0.3048 m\)
Therefore, we can infer that 1 foot = 0.3048 m
So,
\(108 in = 2.7432 m\\108 ft = 32.9184 m\\12 ft = 3.6576m\\\)
Now it is a standard that 1 yard equal to 0.3048 meter
Meter: SI unit of length which equals to 100 cm and is the internationally accepted unit for length.Conversion of length: It is the process by the length of one unit is converted to the length of other units using mensuration rules for e.g., 1 meter = 100 centimeters
This question is a classic example to the conversion of length from one unit to another.
To learn more about unit conversion, click on the link given below:
https://brainly.com/question/27971860
#SPJ9
I want to know if anyone can help with a math textbook. It is page 302, evens only. Skip word problems. Show work if you can, if you can't, then it's alright.

Answers
Step-by-step explanation:
Hopefully I'm right,but what you do is add the ones with variables together so
Question 15
3a + 2 + 3a + 7so 3a+3a= 6a and 7+2=9
so you have to add the ones that are similar but never add
3a+7 because they are not the same37. 5x-2y
38. -3a+2b
Suppose x = 9 is a solution to the equation f(x) = g(x). If a table of values for the equation y = f(x) contains an x-value of 9 and a corresponding y-value of 18, then which of these statements is correct about a table of values for the equation y = g(x)?
A
If it contains an x-value of 9, the corresponding y-value must be 9.
B
If it contains an x-value of 9, the corresponding y-value must be 18.
C
If it contains a y-value of 18, the corresponding x-value must be 9.
D
If it contains a y-value of 18, the corresponding x-value must be 18.
Answers
Answer:
I think it may be A
Step-by-step explanation:
Which statement is true? Group of answer choices 8.01 is a smaller increase in sales then 8.001. A debt of $17 is a larger value than a debt of $20. LaTeX: \frac{2}{3} 2 3 below zero is a lower temperature than 6 below zero. One half an apple is equivalent to 8 fourths apples.
Answers
Answer: The only true statement is:
" A debt of $17 is a larger value than a debt of $20."
Step-by-step explanation:
Let's analyze the options:
A) " 8.01 is a smaller increase in sales then 8.001"
Here you can see the difference:
8.01 - 8.001 = 0.009
The difference is positive, then 8.01 > 8.001.
Then as we are talking of increases in sales, the numbers are positive, then we have that 8.01 is a larger increase in sales than 8.001.
B) "A debt of $17 is a larger value than a debt of $20."
A debt is written as a negative number, then:
A debt of $17 is written as -$17, and a debt of $20 is written as -$20.
Then -$17 is a smaller negative number than -$20
-$17 > -$20
Then this statement is true.
C) " 2/3 bellow zero is lower than 6 bellow zero"
ok, 2/3 bellow zero is: -2/3
6 bellow zero is: -6
-2/3 is larger than -6
-2/3 > -6
then -6 is lower than -2/3, the statement is false.
D) "1/2 of an apple is equivalent to 8/4 apples"
Well, here you can do the quotients:
1/2 = 0.5
8/4 = 2
So these numbers are not equivalents.
The dimensions of a cylinder are shown in the diagram.
5.8cm
7.6cm
Which measurement is closest to the lateral surface area in square centimeters of the cylinder?
Answers
The measurement closest to the lateral surface area of the cylinder is 138.4 cm².
What is surface area?
The area is the area occupied by a two-dimensional flat surface. It has a square unit of measurement. The surface area of a three-dimensional object is the space taken up by its outer surface. Square units are used to measure it as well.
The lateral surface area of a cylinder can be calculated by multiplying the height of the cylinder by the circumference of its base.
The diameter of the base is given as 5.8 cm, so the radius of the base is half of that, or 2.9 cm.
The circumference of the base can be found using the formula C = 2πr, where r is the radius. So,
C = 2 × π × 2.9 cm = 18.212 cm (rounded to two decimal places)
The lateral surface area is then -
Lateral surface area = height × circumference of base
= 7.6 cm x 18.526 cm
= 138.41 cm² ≈ 138.4 cm²
Therefore, the measurement for lateral surface area is 138.4 square centimeters.
To learn more about surface area from the given link
https://brainly.com/question/20771646
#SPJ1

The population of a small town is 1600 and is growing exponentially at a rate of 3% per year. What is the population of the town after 10 years?
people
Answers
Answer:
2150 people
Step-by-step explanation:
You want the number of people in a town after 10 years if the initial population of 1600 is growing at 3% per year.
Exponential growthExponential growth can be modeled by the equation ...
p(t) = a·b^t
where a = p(0) = the initial population, and
b = annual growth factor = (1 + annual growth rate)
ApplicationThe problem statement tells you p(0) = 1600, and the growth rate is 3%. This means the equation modeling the population is ...
p(t) = 1600·1.03^t
Ten yearsThe population in 10 years is modeled as ...
p(10) = 1600·1.03^10 ≈ 2150
The population of the town after 10 years is expected to be about 2150 people.

Suppose you flip a coin and keep a record of the results. In how many ways could you obtain at least one head if you flip the coin seven times
Answers
On flipping a coin, the number of total possibility for obtaining least one head if we flip the coin seven times are equal to 127.
We have an experiment for flip a coin and keep a record of the results.
Number of total possible outcomes on flipping a coin = 2 = { H, T}
Number of trials or a coin is flipped = 7
We have to determine the number of ways that at least one head if we flip the coin seven times. When we flip a two-sided coin n times, there are \(2^ n\) possible outcomes. So, when a coin is flipped 7 times then total possible number of outcomes = 2⁷ = 128
Let's consider an Event A : getting at least one head in seven flips
Complement of this event is getting no head and it is denoted by \(A^ c =\){ T T T T T T T }
and this event will be occur in one way only. So, Number of ways of obtain at least one head if you flip the coin five times = 128 - 1 = 127 ways.
Hence, required value is 127 ways.
For more information about possibility, visit:
https://brainly.com/question/12948766
#SPJ4
PLEASE HELP I WILL MARK BRAINLIEST IF YOURE RIGHT.
The heights of a triangle ABC meet at a point K.AB=CK.Find the angle of C.
Answers
Answer:
45°
Step-by-step explanation:
AD⊥BC, BE⊥AC, CF⊥AB AB = CK
∠1 + ∠2 = 90° ∠5 + ∠2 = 90° ∴ ∠1 = ∠5
∠5 + ∠4 = 90° ∴ ∠4 = ∠2
AB = CK
ΔABD ≅ ΔCKD (ASA)
AD = CD ∴ΔADC is an isosceles triangle
∠C = ∠CAD = 45° (∠C + ∠CAD = 90°)

Which graph represents a system of linear equations that has multiple common coordinate pairs?
sorry if the image is blurry

Answers
Answer:
Step-by-step explanation:
The fourth image because when looking for liner equations if you draw a line through them and it only touches once its linear equation!
sorry if im wrong...
How many solutions exist for the given equation?
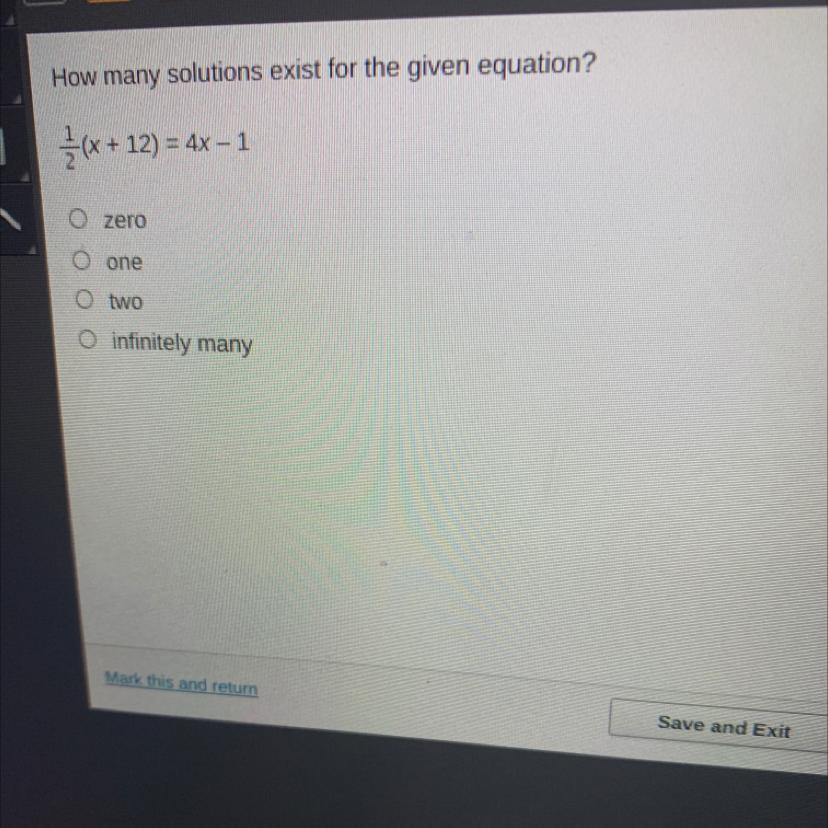
Answers
Answer:
two
Step-by-step explanation:
16 multiply 27 what's the value of x.
Answers
Answer:
bob
Step-by-step explanation:
In triangle ABC, point D lies on side BC such that ΔABD and ΔACD have the same perimeter. Points E and F are constructed on sides CA and AB in a similar manner, respectively, each dividing ΔABC into two triangles of equal perimeter. If BD=5, DC=3, and the perimeter of ΔABC is 18, what is the ratio of the area of ΔDEF to the area of ΔABC?
Answers
Answer:
10
Step-by-step explanation:
Nine cards are dealt from a 52-card deck. Write a formula for the probability that three of the five even numerical denominations are represented twice, one of the three face cards appears twice, and a second face card appears once. (Note: Face cards are the jacks, queens, and kings; 2, 4, 6, 8, and 10 are the even numerical denominations.)
Answers
The problem requires us to calculate the probability that three of the five even numerical denominations are represented twice, one of the three face cards appears twice, and a second face card appears once.
To solve the problem, we need to determine the number of possible hands that meet the criteria and divide it by the total possible hands that can be dealt from the deck. We will begin by counting the total number of ways nine cards can be dealt from a 52-card deck. We will use the combination formula, which is:
nCr = n! / r! (n - r)!,
where n is the total number of items and r is the number of items chosen.
Here, n = 52 and r = 9. nCr = 52C9 = 52! / 9! (52 - 9)! = 4,104,398,535.
This is the total number of possible hands that can be dealt from the deck. Now, we will count the number of ways to choose the cards that meet the criteria. We will divide this by the total number of hands to get the probability of the event. We will choose the five even numerical denominations first. There are five even numbers, and we need three of them to be repeated twice. Therefore, we need to choose three of the five, which can be done in 5C3 = 10 ways. Once we have selected the three even numbers, we can select two of them to be repeated twice in 3C2 = 3 ways. The remaining four cards can be selected from the deck in 44C4 ways. Next, we will choose the face cards. We need two face cards, one of which is repeated twice. There are three face cards, and we need to choose two of them, which can be done in 3C2 = 3 ways. One of the two chosen cards can be repeated twice in two ways. The last card can be chosen from the remaining 46 cards in 46 ways. The total number of ways to choose the cards that meet the criteria is the product of all the above combinations, i.e., 10 × 3 × 44C4 × 3 × 2 × 46. Therefore, the probability of the event is:
P(event) = (10 × 3 × 44C4 × 3 × 2 × 46) / 52C9= 0.0000532 (rounded to four decimal places)
The formula for the probability that three of the five even numerical denominations are represented twice, one of the three face cards appears twice, and a second face card appears once, is P(event) = (10 × 3 × 44C4 × 3 × 2 × 46) / 52C9 = 0.0000532 (rounded to four decimal places).
To learn more about combination formula visit:
brainly.com/question/13090387
#SPJ11
help plz/math will give brainlest


Answers
Answer:
area of parallelogram = 21
area of trapezoid = 32
Step-by-step explanation:
Hello There!
The first figure shown is a parallelogram and the following dimensions are given
base = 7mm
height = 3mm
The area of a parallelogram can simply be found by multiplying the base by the height
so Area = 7 * 3
7 * 3 =21 so the area of the parallelogram is 21 square millimeters
The second figure given is a trapezoid and the following dimensions are given
height = 4m
base 1 = 5m
base 2 = 11m
To find the area of a trapezoid we use this formula
\(A=\frac{a+b}{2} h\)
where a and b are bases and h = height
given the dimensions all we have to do is plug in the values into the formula
\(A=\frac{5+11}{2} 4\\5+11=16\\\frac{16}{2} =8\\8*4=32\\A=32\)
so we can conclude that the area of the trapezoid is 32 square meters
Solve the system by substitution.
y = -2x + 16
y = 2x
Answers
Answer: y = 8 , x = 4
Step-by-step explanation:
gosh darn i haven done this since algebra 1 !!
since both equations equal y, we can make them equal to each other since y = y
-2x +16 = 2x (im just gonna simplify without all the extra steps sorry)
x = 4 (this is the first answer)
now we can plug in x to find y
y = 2(4)
y = 8 (second answer)
im sorry if the grammar is horrid its 3 am
Two functions, f and g are defined on R, the set of real numbers, by f(x)=x²-5 and g(x) = 3x - 1. Find f(g(x)).
Answers
Answer:
f(g(x)) = 9x² - 6x - 4
Step-by-step explanation:
f(g(x) )
= f(3x - 1)
= (3x - 1)² - 5 ← expand factor using FOIL
= 9x² - 6x + 1 - 5
= 9x² - 6x - 4
>
<
=
pls help i beg u
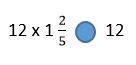
Answers
Answer:
its less than <
Step-by-step explanation:
........
Answer:
>
Step-by-step explanation:
\(12 \times 1 \frac{2}{5} = 12 \times \frac{7}{5} = \frac{60}{5} \times \frac{7}{5} = \frac{420}{25} = 16 \frac{20}{25} \)
Find the value of the missing variable(s)?

Answers
Answer:
x = 163°
Step-by-step explanation:
The sum of interior angles of a pentagon is 540°. The missing value will bring the total to that. It can be found by subtracting the known values from 540°.
__
x = 540° -85° -103° -121° -68°
x = 163°
_____
Additional comment
The sum of interior angles of a simple n-gon is found from the formula ...
angle sum = 180°·(n -2)
For n = 5, this is 180°×3 = 540°.