Answers
17- 3.17-3- 8/3

Related Questions
Renae and her family are on vacation. During the drive from Denver to Rocky Mountain National Park, she saw 48 travel trailers and 27 motor homes. Write the ratio of motor homes to travel trailers three different ways i already got 27:48 27 to 48 i need one more pls help
Answers
Answer: \(\frac{27}{48}\)
The ratio of motor homes to travel trailers in three different ways can be written as 27 : 48, 9 : 16 and 18 : 32.
What is Ratio?Ratio is defined as the relationship between two quantities where it tells how much one quantity is contained in the other.
The ratio of a and b is denoted as a : b.
Given that,
Number of travel trailers that Renae saw = 48
Number of motor homes she saw = 27
We have to find their ratio.
Ratio of motor homes to travel trailers = 27 / 48
Both are multiples of 3. So we can simplify this.
Ratio of motor homes to travel trailers = 9/16
Multiplying numerator and denominator with 2,
Ratio of motor homes to travel trailers = 18/32
Hence the ratio can be 27 : 48, 9 : 16 and 18 : 32.
Learn more about Ratio here :
https://brainly.com/question/1504221
#SPJ2
i need help asap)))))))))))))))))))))

Answers
Answer: a
Step-by-step explanation:
u do 1+1
4×(-5)÷(-2) my name is mirtha
Answers
Do PEMDAS to find your answer.
Hi mirtha
How do I solve this equation?

Answers
Step-by-step explanation:
first u gotta make the solutions on the other side a negative then keep the positive so now you've gotten rid of the lines so now I gotta solve both 4x-3<7 and 4x-3<-7 then solve liek you regular would with moving the 3 to the other side
4x<10 and 4x<-4 then divide both of them by the number itself to get x by itself
A number, y, subtracted from 10

Answers
Answer:
y subtracted from 10 is
10 - y
Hope it will help :)
Answer: D: 10 - y
Step-by-step explanation:
we can rule out option B and C since there isn't a subtraction sign
so now we have A and D
The answer isn't A because thats 10 being subtracted from y
Order 4 of the following sentences so that they prove the following statement by contrapositive. The average of three real numbers is greater than or equal to at least one of the numbers. Choose from this list of sentences Proof by contrapositive of the statement (in order) Hence, the assumption that the average of three real numbers is less than all of the numbers is false This contradicts the fact that +y+z=2+y+z Let , y and be real numbers and (x+y++)/3<1 (+y+)/3 <3 and (x+y+)/3<3 Adding up the three inequalities yields +y+=> +y+2 Hence, the assumption that the average of three real numbers is greater than all of the numbers is false Adding up the three inequalities yields y+<+y+z Letry and be real numbers and (1 + y + 3)/3 > z. (x + y + 2)/3 > y, and (x + y + 3)/3 > x
Answers
The following is the proof by contrapositive of the statement: The average of three real numbers is greater than or equal to at least one of the numbers. Hence, the assumption that the average of three real numbers is less than all of the numbers is false.
The following is the proof by contrapositive of the statement: The average of three real numbers is greater than or equal to at least one of the numbers. Hence, the assumption that the average of three real numbers is less than all of the numbers is false.
Let y and z be real numbers. We assume that (y + z)/2 < y and (y + z)/2 < z. Adding the two inequalities yields y + z < 2y + 2z, which simplifies to y + z < y + z + 2(y + z)/2.
This contradicts the fact that y + z = 2(y + z)/2. Therefore, the assumption that the average of three real numbers is less than all of the numbers is false.
Let x, y, and z be three real numbers. We assume that (x + y + z)/3 < x, (x + y + z)/3 < y, and (x + y + z)/3 < z.
Adding up the three inequalities yields x + y + z < 3x + 3y + 3z, which simplifies to (x + y + z)/3 < (x + y + z)/3 + 2(x + y + z)/3. This contradicts the fact that (x + y + z)/3 = (x + y + z)/3.
Hence, the assumption that the average of three real numbers is greater than all of the numbers is false. Therefore, the proof by contrapositive of the statement (in order) is: Let x, y, and z be three real numbers.
We assume that (x + y + z)/3 < x, (x + y + z)/3 < y, and (x + y + z)/3 < z.
Adding up the three inequalities yields x + y + z < 3x + 3y + 3z, which simplifies to (x + y + z)/3 < (x + y + z)/3 + 2(x + y + z)/3.
This contradicts the fact that (x + y + z)/3 = (x + y + z)/3.
Hence, the assumption that the average of three real numbers is greater than all of the numbers is false. Let y and z be real numbers. We assume that (y + z)/2 < y and (y + z)/2 < z. Adding the two inequalities yields y + z < 2y + 2z, which simplifies to y + z < y + z + 2(y + z)/2. This contradicts the fact that y + z = 2(y + z)/2. Therefore, the assumption that the average of three real numbers is less than all of the numbers is false.
To know more about real numbers visit:
https://brainly.com/question/31715634
#SPJ11
What is...
2 + 2?
yes this is for easy points
Answers
Answer: 4?
Step-by-step explanation: hehe
(is brainliest to much to ask for?) THaNK YOU
Answer:
2+2=4
Thanks for points!! :)
Which is the best estimate for the value of r in the scatter plot? 40 PTS!!

Answers
The best estimate for the value of r in the given scatter plot is -0.9.
Here, we are given a scatter plot as shown in the figure above.
To estimate the value of r in the scatter plot, we don't actually need to calculate the value of r. We can infer the value by looking at the scatter plot.
As we can see the points show a downward trend so it must be the case that the r value will be negative.
Thus, we can easily eliminate option 1 and 3 as they are positive values.
Now, we've two options: -0.9 and -1
-1 represents a perfect negative correlation, but as we can see from the graph, the points do not form a perfectly straight line. This means that r value cannot be -1.
Thus, we can say that the best estimate of the value of r in the scatter plot is -0.9.
Learn more about scatter plots here-
https://brainly.com/question/26270713
#SPJ1
if x is a continuous random variable then p(x=a)
Answers
For a continuous random variable x, the probability of x taking on a specific value a is zero. This is due to the infinite number of possible values that x can take on within its range.
In the case of a continuous random variable, the probability density function (PDF) describes the likelihood of x taking on different values. Unlike discrete random variables, which can only take on specific values with non-zero probabilities, a continuous random variable can take on an infinite number of values within a given range. Therefore, the probability of x being equal to any specific value, such as a, is infinitesimally small, or mathematically speaking, it is equal to zero.
To understand this concept, consider a simple example of a continuous random variable like the height of individuals in a population. The height can take on any value within a certain range, such as between 150 cm and 200 cm. The probability of an individual having exactly a height of, say, 175 cm is extremely low, as there are infinitely many possible heights between 150 cm and 200 cm.
Instead, the probability is associated with ranges or intervals of values. For example, the probability of an individual's height being between 170 cm and 180 cm might be nonzero and can be calculated using integration over that interval. However, the probability of having an exact height of 175 cm, as a single point on the continuous scale, is zero.
Learn more about probability density function here: https://brainly.com/question/31039386
#SPJ11
the expected value for a binomial probability distribution is group of answer choices e(x) = pn(1 - n) e(x) = p(1 - p) e(x) = np e(x) = np(1 - p)
Answers
The correct answer is e(x) = np. The expected value for a binomial probability distribution is given by the formula e(x) = np, where n represents the number of trials and p represents the probability of success in each trial.
The expected value is a measure of the average or mean outcome of a binomial experiment. It represents the number of successful outcomes one would expect on average over a large number of trials.
The formula e(x) = np arises from the fact that the expected value of a binomial distribution is the product of the number of trials (n) and the probability of success (p) in each trial. This is because in a binomial experiment, the probability of success remains constant for each trial.
Therefore, to calculate the expected value of a binomial probability distribution, we multiply the number of trials by the probability of success in each trial, resulting in e(x) = np.
Learn more about binomial here:
https://brainly.com/question/30339327
#SPJ11
Simplify √-24 usingimaginary i
Answers
Given:
\(\sqrt{-24}\)Apply the laws of exponents:
\(=\sqrt{-1}\sqrt{24}\)Apply the properties of imaginary numbers:
\(i\sqrt{24}\)Rewrite in standard complex form:
\(2\sqrt{6}i\)Answer:
\(2\sqrt{6}\text{ i}\)find the slope between (0, 6) and (-3,9)
Answers
Answer:
-1
Step-by-step explanation:
The formula for finding a slope is: m = (change in y)/(change in x)
Find the change in each value
Y: 9 - 6 = 3
X: -3 - 0 = -3
Input the values
m = 3/-3
m = -1
I would start this problem by setting up a table.
In the left column, we will have our x values
and in the right column, we have our y values.
Put our first ordered pair on the top and second on bottom.
We can see the y values go from 6 to 9 so change in y is 3.
The x values go from 0 to -3 so change in x is -3.
The slope is equal to the rate of change or change in y / change in x.
So our slope is 3/-3 of -1.
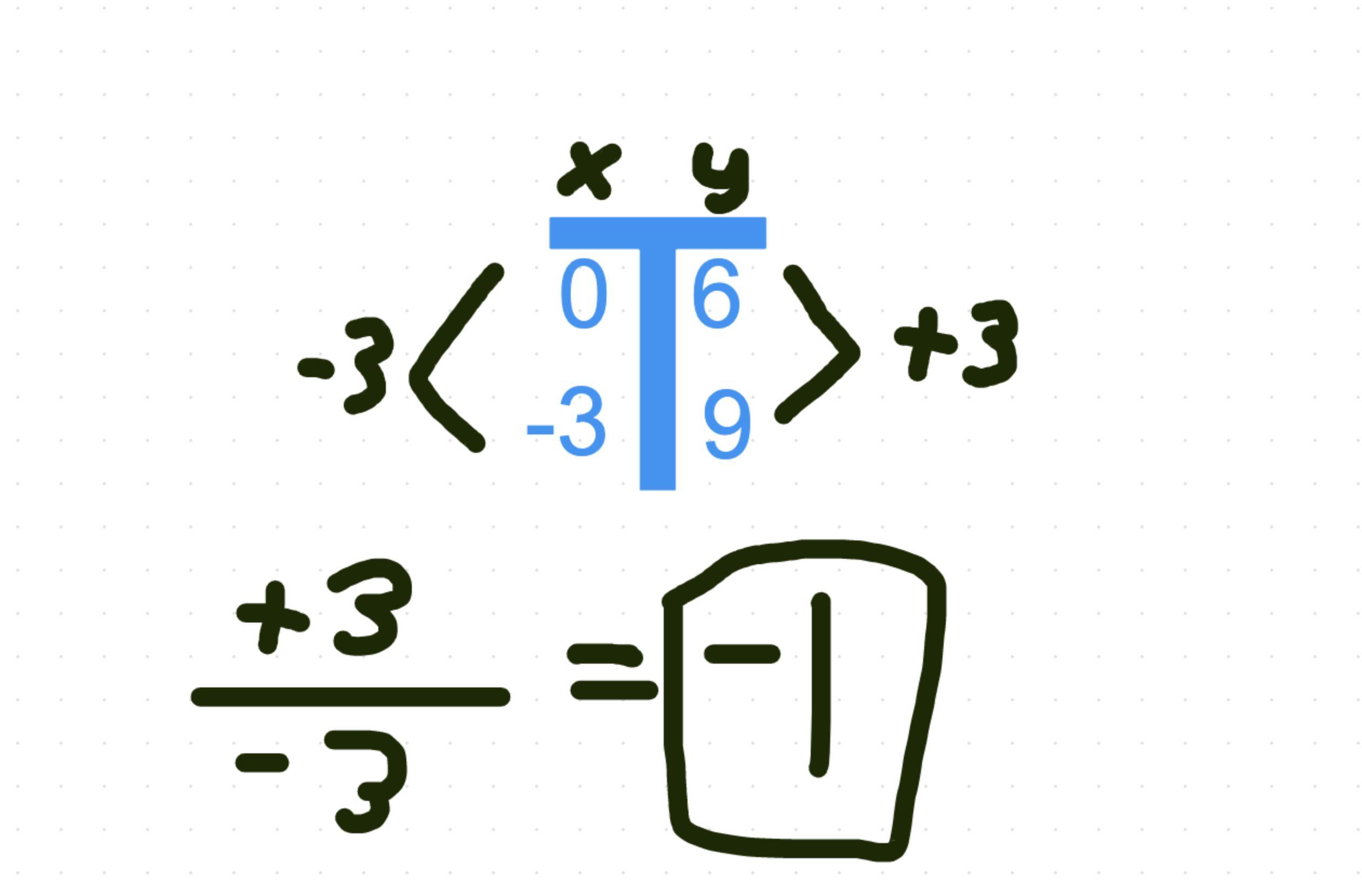
At generic Middle school 6 students were sick with the flu on the first week of school. During the second week 10 students were sick and on the third week there were 15 students sick. The attendance clerk noticed that the number of students getting sick was growing exponentially with a growth factor of ‘1.6. Week#1(6) Week#2(10) Week#3(15). If the model continues to be correct for at least the first 3 months how many would be sick on the 12th week of school. Someone please give me a written explanation for this
Answers
If the model is true, there would be around 1689 students sick during the 12th week of classes.
The number of students getting sick was growing exponentially with a growth factor of ‘1.6.
Week 1 : (6)
Week 2 : (10)
Week 3 : (15).
To find the number of students sick on the 12th week of school, we can use the formula for exponential growth:
y = a bˣ
Where:
y is the number of students sick on the x th week
a is the number of students sick on the first week (6 in this case)
b is the growth factor (1.6 in this case)
x is the number of weeks that have passed (12 in this case)
Plugging in the values, we get:
y = 6 · 1.6¹²
Solving for y, we get:
y = 6 · 281.47
y = 1688.8 ≈ 1689
Therefore, there would be approximately 1689 students sick on the 12th week of school if the model is correct.
Learn more about exponential function here:
brainly.com/question/11487261
#SPJ1
Use a parameterization to find the flux doubleintegral_S F middot n do of F = 5xy i - 2z k outward (normal away from the z-axis) through the cone z = 6 squareroot x^2 +y^2 0 lessthanorequalto z lessthanorequalto 6. The flux is (Type an exact answer, using pi as needed.)
Answers
The flux of the vector field F through the cone is zero.
To find the flux of the vector field F = 5xy i - 2z k outward through the cone z = 6 square root x^2 +y^2 with 0 ≤ z ≤ 6, we need to first parameterize the cone. Let x = r cos θ and y = r sin θ, where r ≥ 0 and 0 ≤ θ ≤ 2π, then we have z = 6r for the cone.
Now we can compute the unit normal vector n as n = (zr/6) cos θ i + (zr/6) sin θ j + (z/6) k, and then calculate the dot product F · n as F · n = 5xy (zr/6) - 2z (z/6) = (5/6)zr^2 cos θ sin θ - z^2/3.
The double integral of F · n over the cone is then given by:
doubleintegral_S F · n dS = doubleintegral_R (5/6)zr^2 cos θ sin θ - z^2/3 r dr dθ
where R is the region in the xy-plane that corresponds to the base of the cone.
Integrating with respect to r first, from 0 to 6, we get:
doubleintegral_S F · n dS = integral_0^(2π) integral_0^6 (5/18)z^3 cos θ sin θ - (1/9)z^3 r dr dθ
Evaluating the integral with respect to r and then θ, we obtain:
doubleintegral_S F · n dS = 0
To learn more about vector field :
https://brainly.com/question/17177764
#SPJ11
If people prefer a choice with risk to one with uncertainty they are said to be averse to
Answers
If people prefer a choice with risk to one with uncertainty, they are said to be averse to uncertainty.
Uncertainty and risk are related concepts in decision-making under conditions of incomplete information. However, they represent different types of situations.
- Risk refers to situations where the probabilities of different outcomes are known or can be estimated. In other words, the decision-maker has some level of knowledge about the possible outcomes and their associated probabilities. When people are averse to risk, it means they prefer choices with known probabilities and are willing to take on risks as long as the probabilities are quantifiable.
- Uncertainty, on the other hand, refers to situations where the probabilities of different outcomes are unknown or cannot be estimated. The decision-maker lacks sufficient information to assign probabilities to different outcomes. When people are averse to uncertainty, it means they prefer choices with known risks (where probabilities are quantifiable) rather than choices with unknown or ambiguous probabilities.
In summary, if individuals show a preference for choices with known risks over choices with uncertain or ambiguous probabilities, they are considered averse to uncertainty.
If people prefer a choice with risk to one with uncertainty, they are said to be averse to uncertainty.
To know more about uncertainty, visit
https://brainly.com/question/16941142
#SPJ11
a straight line is given to pass through the points (1, 5) and (2, 8). the equation of the straight line is of the form y
Answers
y = 3x + 2
The equation of the straight line passing through the points (1, 5) and (2, 8) is y = 3x + 2?
To find the equation of a straight line passing through two given points, we can use the point-slope form of the equation:
y - y₁ = m(x - x₁)
where (x₁, y₁) and (x, y) are the coordinates of the points, and m is the slope of the line.
Given the points (1, 5) and (2, 8), we can substitute these values into the equation:
y - 5 = m(x - 1)
Next, we need to find the value of the slope, m. The slope is given by the formula:
m = (y₂ - y₁) / (x₂ - x₁)
Substituting the values of the points into the formula:
m = (8 - 5) / (2 - 1)
m = 3 / 1
m = 3
Now we can substitute the value of the slope, m = 3, into the equation:
y - 5 = 3(x - 1)
Simplifying the equation:
y - 5 = 3x - 3
Adding 5 to both sides:
y = 3x + 2
So, the equation of the straight line passing through the points (1, 5) and (2, 8) is y = 3x + 2.
Learn more about y = 3x + 2
brainly.com/question/30487757
#SPJ11
the mean of a distribution is defined as the data value where 50% of the data is above and 50% is below. group of answer choices true false
Answers
FALSE, it is not the mean but the median of a distribution which is defined as the data value where 50% of the data is above and 50% is below.
The median denotes the point at which 50% of data values are higher and 50% are lower. As a result, it is the data's midpoint. In a symmetrical distribution, the median is always the midpoint, resulting in a mirror image with the median in the center.
The median is the number in the middle of a sorted, ascending or descending list of numbers, and it might be more descriptive of the data set than the average.
To know more about median refer to:
brainly.com/question/28060453
#SPJ4
In September 1990, a random sample of 200 biology major students at a large university was
asked how many lab classes he or she was enrolled. The sample results below
Number of lab classes 0-1 2-3 4-5
Number of students 90 87 23
To determine whether the distribution has changed over the past 10 years, a similar survey was conducted
in September 2000 by selecting a random sample 200 biology major.
Number of lab classes 0-1 2-3 4-5
Number of students 92 70 38
a. Do the data provide evidence that the proportion of students who took 4-5 lab class in September 2000
was different from that in 1990? Use α = 0.05. Report both RR and p-value
b. Does the answer in (a) address the question whether the distribution of number of lab classes was
different in 2000 than it was in 1990, at significance level 0.05? Explain why your answer is "Yes" or
"No". If "No", no actual test is needed
Answers
a. The RR (relative risk) cannot be calculated for this type of test, and we do not need to report a p-value for the chi-squared goodness-of-fit test. b. No, the answer in (a) does not address the question whether the distribution of number of lab classes was different in 2000 than it was in 1990.
a. To test if the proportion of students who took 4-5 lab classes in September 2000 was different from that in 1990, we will use a chi-squared goodness-of-fit test.
First, we need to calculate the expected frequencies for each category assuming the null hypothesis is true (i.e., the proportions are the same in 1990 and 2000). We can calculate the expected frequencies as follows:
Expected frequency for 0-1 lab classes: (90+92+87+70+23+38) * (90/200) = 103.5
Expected frequency for 2-3 lab classes: (90+92+87+70+23+38) * (87/200) = 90.3
Expected frequency for 4-5 lab classes: (90+92+87+70+23+38) * (23/200) = 10.2
Next, we can calculate the chi-squared test statistic as follows:
χ2 = Σ (O - E)2 / E
where O is the observed frequency and E is the expected frequency.
Using the data provided, we have:
χ2 = [(90 - 103.5)2 / 103.5] + [(87 - 90.3)2 / 90.3] + [(23 - 10.2)2 / 10.2] + [(92 - 103.5)2 / 103.5] + [(70 - 90.3)2 / 90.3] + [(38 - 10.2)2 / 10.2] = 43.17
The degrees of freedom for the chi-squared test is df = number of categories - 1 = 3 - 1 = 2. Using a significance level of α = 0.05 and a chi-squared distribution table with df = 2, the critical value is 5.99.
Since our calculated test statistic (χ2 = 43.17) is greater than the critical value (5.99), we reject the null hypothesis and conclude that there is evidence that the proportion of students who took 4-5 lab classes in September 2000 was different from that in 1990.
The RR (relative risk) cannot be calculated for this type of test, and we do not need to report a p-value for the chi-squared goodness-of-fit test.
b. No, the answer in (a) does not address the question whether the distribution of number of lab classes was different in 2000 than it was in 1990. The chi-squared goodness-of-fit test only tests whether the proportions in the three categories are the same between 1990 and 2000, but it does not tell us whether the overall distribution has changed. To address this question, we could use a chi-squared test for independence, which would allow us to test whether there is a relationship between the year (1990 vs. 2000) and the number of lab classes taken.
Learn more about distribution here
https://brainly.com/question/29368683
#SPJ11
What is the volume, in cubic inches, of the prism

Answers
Answer:
volume = 130 in ^3
Step-by-step explanation:
volume = 5x8x3.25 = 130 in ^3
What fraction is equivalent to 1/6
A. 3/8
B. 2/8
C. 3/24
D. 4/24
Answers
Answer:
C
Step-by-step explanation:
Because 24 divided by 3 = 8 and 3/8 has a denominator of 8 and you divide it by 3
could i have branliest and a heart please
Have a good day :)
Find the value of y.
148°
y
x
y = [?]°
![Find the value of y.148yxy = [?]](https://i5t5.c14.e2-1.dev/c-qa-images/contents/attachments/wypnyTl7qtcloD5K5APssJ1mBYaWwhr3.png)
Answers
Answer:
y=90 degree
Step-by-step explanation:
bcz this triangle is drawn in the semi-circle and the greatest angle of triangle in a semi-circle is always right angle.
(-4,-2) (0,2) (-2,1) find the domain and range and can you tell me if it’s a function ?? PLS HELPPP
Answers
Answer:
domain means -4,0,-2 and range is -2,2,1
Please help! I will give BRAINLIEST! Find Y.

Answers
Answer:
y = 30
Step-by-step explanation:
the 2 marked sides are congruent, thus the triangle is isosceles with the 2 base angles being congruent, both (y + 24)°
The exterior angle of a triangle is equal to the sum of the 2 opposite interior angles.
(4y - 12)° is an exterior angle of the triangle , then
4y - 12 = y + 24 + y + 24
4y - 12 = 2y + 48 ( subtract 2y from both sides )
2y - 12 = 48 ( add 12 to both sides )
2y = 60 ( divide both sides by 2 )
y = 30
Help meee please..............,..................
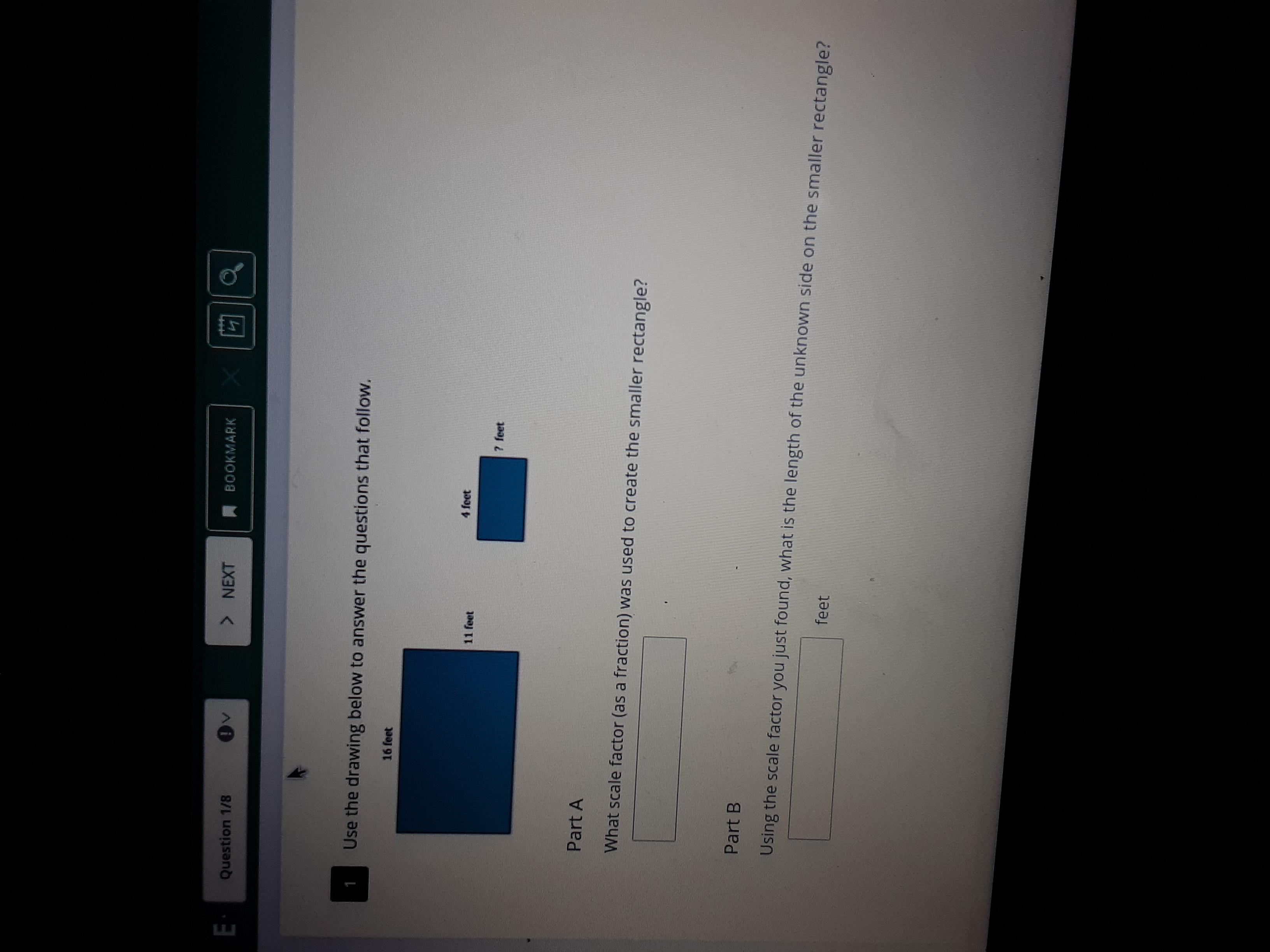
Answers
Answer:
It is a scale factor of 1/4
the missing side length is 2.75
Step-by-step explanation:
Use Matlab to plot the function f(x) = - 4x² + sin(5x) and its derivative on the same plot for x between -10 and 10, in steps of 0.5 with appropriate legend and axis labels (use a dashed red line for f(x) and a solid blue line for its derivative). The derivative of f(x) is: (-4x² + sin(57x)) = - 8x + 5π cos(5x) dx Also, create an output file named "results.txt" and write x, f(x) and its derivative into the file. Use 2 decimal places. X f(x) df/dx
Answers
To plot the function f(x) = -4x^2 + sin(5x) and its derivative, and to save the results in a file named "results.txt" with 2 decimal places.
You can use the following MATLAB code:
```matlab
x = -10:0.5:10; % Generate x values
f = -4*x.^2 + sin(5*x); % Calculate f(x)
df_dx = -8*x + 5*pi*cos(5*x); % Calculate the derivative
% Saving results to file
output = [x', f', df_dx'];
dlmwrite('results.txt', output, 'delimiter', '\t', 'precision', '%.2f');
1. First, we define the range of x values using the vector `-10:0.5:10` to cover the desired interval with a step size of 0.5.
2. Next, we calculate the values of f(x) and its derivative using the defined mathematical expressions.
3. We then plot the function and its derivative using the `plot` function. The red dashed line represents f(x), and the blue solid line represents its derivative.
4. To save the results, we create a matrix `output` that concatenates the x values, f(x), and the derivative column-wise.
Learn more about decimal places here: brainly.com/question/20563248
#SPJ11
what is s for the following function

Answers
11=3s+2
-2. -2
9=3s
9/3
=3
Answer:
S = 3
S = 5
S = 7
S = 9
Step-by-step explanation:
t = 3s + 2
when t = 11
11 = 3s + 2
11 – 2 = 3s
9 = 3s
s = 3
t = 3s + 2
when t = 17
17 = 3s + 2
17 – 2 = 3s
15 = 3s
s = 5
t = 3s + 2
when t = 23
23 = 3s + 2
23 – 2 = 3s
21 = 3s
s = 7
t = 3s + 2
when t = 29
29 = 3s + 2
29 – 2 = 3s
27 = 3s
s = 9
I HOPE ALL THIS HELPS
RATE AS BRAINLIEST PLS
Complete the table for the given rule.
Rule: y = 2 – 3
7.
1
7

Answers
Step-by-step explanation:
y = x-3
So, y + 3 = x
x = y + 3
if x = 7
y = 7 - 3 = 4
if y = 1
x = 1 + 3 = 4
......
the two-way table shows the attendant careers among the incoming class of first-year college students, divided by gender. If a female student is chosen at random, what is the probability that she intends to be a research scientist?

Answers
Answer: 4.64%
\(\dfrac{\text{female research scientist}}{\text{female total}}=\dfrac{103}{2219}=0.0464\quad =\large\boxed{4.64\%}\)
Anyone know the right answer?!

Answers
Answer:
420000 here is the answer
Step-by-step explanation:
28000 multipli 15
7^x=3^[x+4] solve x using logarithmic
Answers
By taking advantage of the definition of exponential and logarithmic function and their inherent relationship we conclude that the solution is x = 4 · ㏒ 3/(㏒ 7 - ㏒ 3).
How to solve an exponential equation by logarithms
Exponential and logarithmic functions are trascendental functions, these are, functions that cannot be described algebraically. In addition, logarithmic functions are the inverse form of exponential functions. In this question we take advantage of this fact to solve a given expression:
7ˣ = 3ˣ⁺⁴ Given㏒ 7ˣ = ㏒ 3ˣ⁺⁴ Definition of logarithmx · ㏒ 7 = (x + 4) · ㏒ 3 ㏒ aᵇ = b · ㏒ ax · ㏒ 7 = x · ㏒ 3 + 4 · ㏒ 3 Distributive propertyx · (㏒ 7 - ㏒ 3) = 4 · ㏒ 3 Existence of additive inverse/Modulative and associative propertiesx = 4 · ㏒ 3/(㏒ 7 - ㏒ 3) Existence of multiplicative inverse/Modulative property/ResultBy taking advantage of the definition of exponential and logarithmic function and their inherent relationship we conclude that the solution is x = 4 · ㏒ 3/(㏒ 7 - ㏒ 3).
To learn more on logarithms: https://brainly.com/question/20785664
#SPJ1
