Answers
Answer:
C
Step-by-step explanation:
Related Questions
3 drinks and 2 pretzels costs $16, but 6 drinks and 5 pretzels ests $21.25. What is the press
of one pretzel?
Answers
6d + 10p = 32.00
6d + 5p = 21.25
Use elimination
5p = 10.75
Divide by 5
p = 2.15
Answer: one pretzel is $2.15
Answer:
The price of one pretzel is $-10.75
Step-by-step explanation:
I'm not really sure why the pretzel would be negative dollars, but I checked my answer multiple times and it's right. For this problem you need a system of equations. The system will be 3d+2p=16 (since 3 drinks and 2 pretzels is 16 dollars) and 6d+5p=21.25 (since 6 drinks and 5 pretzels is 21.25 dollars). To solve this system, the first thing we're going to do is multiply the first system by -2 so that we can cancel the d variable. This will leave you with
-6d-4p=-32. Now, you can add this to the other equation. Since the -6 and 6 cancel, we only have the p variable now (that's why we multiplied by -2, to cancel out the d variable when we added later). Now we have -4p=-32 and 5p=21.25. Add these two equations together and you'll get 1p=-10.75, or p=-10.75. If you needed to solve for the drinks, you could plug -10.75 back into one of the first two equations, but for this problem we don't so -10.75 is your answer.
Find the solution of the differential equation that satisfies the given initial condition. 5. (ex + y)dx + (2 + x + yey)dy = 0, y(0) = 1 6. (x + y)2dx + (2xy + x2 – 1)dy = 0, y(1) = 1
Answers
5. The solution to the differential equation (ex + y)dx + (2 + x + yey)dy = 0 with y(0) = 1 is y = 2e^(-x) – x – 1. 6. The solution to the differential equation (x + y)²dx + (2xy + x² – 1)dy = 0 with y(1) = 1 is y = x – 1.
5. To solve the differential equation (ex + y)dx + (2 + x + yey)dy = 0 with the initial condition y(0) = 1, we can use the method of exact differential equations. By identifying the integrating factor as e^(∫dy/(2+yey)), we can rewrite the equation as an exact differential. Solving the resulting equation yields the solution y = 2e^(-x) – x – 1.
To solve the differential equation (x + y)²dx + (2xy + x² – 1)dy = 0 with the initial condition y(1) = 1, we can use the method of separable variables. Rearranging the equation and integrating both sides with respect to x and y, we obtain the solution y = x – 1.
These solutions satisfy their respective initial conditions and represent the family of curves that satisfy the given differential equations.
Learn more about Separable variables here: brainly.com/question/30417970
#SPJ11
pls help:(...........———

Answers
Answer:
Just for points sorry
Step-by-step explanation:
Answer:
32
Step-by-step explanation:
6+12+14=32
need help will give brainlist

Answers
Answer:
40
Step-by-step explanation:
Answer:
11 is the answer.
The circulation of a newsletter decreased from 6500 to 3575. What was the percentage decrease in circulation?
Answers
Answer:
Step-by-step explanation:
6
Pls help
6x+1+x+7 solve for x
Answers
6x ➕1 ➕ x + 7
Add the numbers, these numbers are 1 and 7.
6x ➕ 8 ➕ xCombine like terms.
7x ➕ 8Let S be the subspace of R3 given by S = Span *** ((:)) 2 Find a basis for S.
Answers
A basis for S is {a, b} = {(1, 2, 0), (-1, 1, 2)}.
In the given question, S is the subspace of R3 given by S = Span{a, b}, where a = (1, 2, 0) and b = (-1, 1, 2). We need to find a basis for S.A basis for S can be defined as the minimum set of vectors that span S.
Therefore, to find a basis for S, we need to check whether {a, b} is a linearly independent set or not.
Linearly independent set: A set of vectors {v1, v2, ..., vn} is linearly independent if the only solution to the equation a1v1 + a2v2 + ... + anvn = 0 is a1 = a2 = ... = an = 0.
If there are other non-zero solutions, then the set of vectors is linearly dependent. This means that at least one vector in the set can be represented as a linear combination of the others.In the given problem, we will solve the equation a1a + a2b = 0, where a1 and a2 are scalars.If we take a1 = 1 and a2 = -1, then a1a + a2b = (1)(1, 2, 0) + (-1)(-1, 1, 2) = (2, 1, -2).
Since (2, 1, -2) is not equal to the zero vector, this implies that {a, b} is a linearly independent set. Hence, {a, b} is a basis for S.Therefore, a basis for S is {a, b} = {(1, 2, 0), (-1, 1, 2)}.
Hence, the solution is as follows:A basis for S is {a, b} = {(1, 2, 0), (-1, 1, 2)}.The above explanation can be formulated into a 150 words answer as follows:A basis for a subspace S of R3 can be found using the minimum set of vectors that spans the subspace S. In this problem, a subspace S of R3 is given by S = Span{a, b}, where a = (1, 2, 0) and b = (-1, 1, 2). We are required to find a basis for S.
To check whether {a, b} is a linearly independent set or not, we will solve the equation a1a + a2b = 0, where a1 and a2 are scalars.
On solving this equation, we get a1 = 1, a2 = -1, and (2, 1, -2) is not equal to the zero vector, which implies that {a, b} is a linearly independent set.
Therefore, {a, b} is a basis for S. Hence, a basis for S is {a, b} = {(1, 2, 0), (-1, 1, 2)}.
Know more about basis here,
https://brainly.com/question/30451428
#SPJ11
Indiv Schedule X-Single The tax is: If taxable income is over: But not over: 10% of taxable income 0 $ 9,950 $ $9.950 $ 40,525 $ 40,525 $ 86,375 $164,925 $209,425 $ 86,375 $995 plus 12% of the excess over $9,950 $4,664 plus 22% of the excess over $40,525 $14,751 plus 24% of the excess over $86,375 $33,603 plus 32% of the excess over $164,925 $47,843 plus 35% of the excess over $209,425 $157,804.25 plus 37% of the excess over $523,600 $164,925 $ 209,425 $ 523,600 $ 523,600 - Schedule Y-1-Married Filing Jointly or Qualifying Widow(er) If taxable income is over: But not over: The tax is: $ 0 $ 19,900 10% of taxable income $ 19,900 $ 81,050 $172,750 $ 81,050 $1,990 plus 12% of the excess over $19,900 $172,750 $9,328 plus 22% of the excess over $81,050 $329,850 $29,502 plus 24% of the excess over $172,750 $418,850 $67,206 plus 32% of the excess over $329,850 $628,300 $95,686 plus 35% of the excess over $418,850 $168.993.50 plus 37% of the excess over $628,300 $ 329,850 $418,850 $ 628,300 - Schedule Z-Head of Household If taxable income is over: But not over: The tax is: $ 0 $ 14,200 10% of taxable income $ 14,200 $ 54,200 $ 54,200 $ 86,350 $ 86,350 $164,900 $ 164,900 $209,400 $ 523,600 $1,420 plus 12% of the excess over $14,200 $6,220 plus 22% of the excess over $54,200 $13,293 plus 24% of the excess over $86,350 $32,145 plus 32% of the excess over $164,900 $46,385 plus 35% of the excess over $209,400 $156,355 plus 37% of the excess over $523,600 $ 209,400 $ 523,600 - Schedule Y-2-Married Filing Separately If taxable income is over: But not over: $ 0 $ 9,950 $ 40,525 $ 9,950 $ 40,525 $ 86,375 $164.925 $ 209,425 $314,150 $ 86,375 $164.925 $ 209,425 $314,150 The tax is: 10% of taxable income $995 plus 12% of the excess over $ 9,950 $4,664 plus 22% of the excess over $40,525 $14,751 plus 24% of the excess over $86,375 $33,603 plus 32% of the excess over $164,925 $47,843 plus 35% of the excess over $209,425 $84.496.75 plus 37% of the excess over $314.150 In 2021, Sheryl is claimed as a dependent on her parents' tax return. Her parents report taxable income of $500,000 (married filing jointly). Sheryl did not provide more than half her own support. What is Sheryl's tax liability for the year in each of the following alternative circumstances? Use Tax Rate Schedule. Dividends and Capital Gains Tax Rates for reference. (Leave no answer blank. Enter zero if applicable.) a. She received $7,500 from a part-time job. This was her only source of income. She is 16 years old at year-end. Tax liability b. She received $7,500 of interest income from corporate bonds she received several years ago. This is her only source of income. She is 16 years old at year-end. Tax liability c. She received $7,500 of interest income from corporate bonds she received several years ago. This is her only source of income. She is 20 years old at year-end and is a full-time student. Tax liability d. She received $7,500 of qualified dividend income. This is her only source of income. She is 16 years old at year-end. Tax liability 930
Answers
In all alternative circumstances given, Sheryl's tax liability for the year is zero.
To calculate Sheryl's tax liability in each of the given alternative circumstances, we need to refer to the Tax Rate Schedule provided and consider Sheryl's age and income sources.
a. She received $7,500 from a part-time job. This was her only source of income. She is 16 years old at year-end.
According to the information provided, Sheryl is 16 years old and her only source of income is from a part-time job.
Based on the Tax Rate Schedule for Single individuals:
- The first $9,950 of taxable income is taxed at 10%.
- There is no tax on the portion of income below $9,950.
Since Sheryl's taxable income is $7,500, which is below the threshold of $9,950, her tax liability would be zero.
b. She received $7,500 of interest income from corporate bonds she received several years ago. This is her only source of income. She is 16 years old at year-end.
In this scenario, Sheryl's only source of income is interest income from corporate bonds. Similar to the previous case, we refer to the Tax Rate Schedule for Single individuals.
Again, since Sheryl's taxable income is $7,500, which is below the threshold of $9,950, her tax liability would be zero.
c. She received $7,500 of interest income from corporate bonds she received several years ago. This is her only source of income. She is 20 years old at year-end and is a full-time student.
In this scenario, Sheryl is 20 years old and a full-time student. We need to consider her age and the Tax Rate Schedule for Single individuals.
Based on the Tax Rate Schedule:
- The first $9,950 of taxable income is taxed at 10%.
- The portion of income between $9,950 and $40,525 is taxed at 12%.
Since Sheryl's taxable income is $7,500, which is below the threshold of $9,950, her tax liability would be zero.
d. She received $7,500 of qualified dividend income. This is her only source of income. She is 16 years old at year-end.
In this scenario, Sheryl's only source of income is qualified dividend income. We need to refer to the Tax Rate Schedule and consider her age.
Based on the Tax Rate Schedule for Single individuals:
- Qualified dividends are generally taxed at a lower rate than ordinary income.
For individuals in the 0% capital gains tax bracket (which includes Sheryl), qualified dividends are taxed at a 0% rate.
Since Sheryl's taxable income is $7,500 from qualified dividend income, she falls into the 0% capital gains tax bracket, and her tax liability would be zero.
Learn more about tax liability here:
https://brainly.com/question/31965060
#SPJ4
the length of a rectangular field three times of it's breath.if the area of the field is 675 m2, find the perimeter
with full solution
Answers
L/W = 3/1 or L = 3*W
A = L*W = (3*W)*W = 3*W^2 = 675 m^2
W^2 = (675 m^2)/3 = 225 m^2
W = sqrt(225 m^2) = 15 m
L = 3*W = 3*(15 m) = 45 m
A group of people were asked if Marilyn Monroe had a thing with John F Kennedy. 110 responded "yes", and 163 responded "no". Find the probability that if a person is chosen at random, he does NOT believes Marilyn Monroe had an affair with John.
Probability = ______ (Please enter a reduced fraction.)
Answers
The probability that if a person is chosen at random, he does NOT believes Marilyn Monroe had an affair with John is 0.60 or 60%
How to find the probability that if a person is chosen at random, he does NOT believes Marilyn Monroe had an affair with John
We can find the probability that a person does not believe Marilyn Monroe had an affair with John F Kennedy by dividing the number of people who responded "no" by the total number of people who responded to the survey:
Probability of "no" = Number of "no" responses / Total number of responses
Total number of responses = Number of "yes" responses + Number of "no" responses
Total number of responses = 110 + 163 = 273
Probability of "no" = 163 / 273
Simplifying the fraction, we get:
Probability of "no" = 0.5967 or approximately 0.60
So, the probability that if a person is chosen at random, he does not believe Marilyn Monroe had an affair with John F Kennedy is approximately 0.60, or 60%.
Learn more about probability at:https://brainly.com/question/25870256
#SPJ1
Suppose 30 flour beetles are left undisturbed in a warehouse bin. The beetle populations doubles each week. The function f(x)=30x2^x gives the population after x weeks. How many beetles will there be after 56 days?
Answers
Answer:
240
Step-by-step explanation: 56 / 7 = 8
30 * 8 = 240
A new hospital in Stamford starts out with 10 junior residents and 5 senior residents on its staff. Management plans to hire additional personnel at a rate of 2 junior residents per month and 3 senior residents per month. Eventually, there will be an equal number of each on the hospital staff. How many of each type will there be?
NEED HELP ON THE GRAPH AS WELL

Answers
For an experiment involving 2 Levels of factor A and 3 levels of factor B with a sample of n = 5 in each treatment condition, what is the value for df within treatments?
A 24
B 20
C 29
D 30
Answers
Option A is the correct answer.
For an experiment involving 2 Levels of factor A and 3 levels of factor B with a sample of n = 5 in each treatment condition, we need to calculate the value for df within treatments.
The formula to calculate df within treatments is given by, df within treatments = (A - 1) (B - 1) (n - 1)Where, A = Levels of factor AB = Levels of factor Bn = Sample size= 2 levels of factor A= 3 levels of factor B= 5 in each treatment conditionNow, df within treatments = (A - 1) (B - 1) (n - 1)= (2 - 1) (3 - 1) (5 - 1)= 1 × 2 × 4= 8Hence, the value of df within treatments is 8.
Learn more about factor
https://brainly.com/question/14549998
#SPJ11
The table show the number of tubs of popcorn that a popcorn vendor sold at the baseball games for each month during baseball season. For which situation is the mean the best measure of central tendency to use to describe this set of data? A. If the vendor wants to know the average number of tubs of popcorn sold monthly during the baseball season. B. If the vendor wants to know which month saw the greatest number of sales. C. If the vendor wants to know which month saw the fewest number of sales. D. If the vendor wants to know the number of tubs of popcorn sales for which the number of sales below it and above it were equal.
Answers
explain the meaning and functions of inferentail and factual claims
Answer:
The answer is A.
I just got tired of getting it wrong and guessed

Find the area of region enclosed by the graphs of f(x)=x² −x−5 and f(x)=x+10
Answers
We determined the points of intersection, identified which function is on top in different intervals, and integrated the absolute difference between the functions over the interval [-3, 5].
To find the area of the region enclosed by the graphs of f(x) = x^2 - x - 5 and f(x) = x + 10, we need to determine the points of intersection between the two functions and integrate the absolute difference between them.
First, let's find the points of intersection by setting the two equations equal to each other:
x^2 - x - 5 = x + 10
Rearranging the equation, we get:
x^2 - 2x - 15 = 0
Factoring the quadratic equation, we have:
(x - 5)(x + 3) = 0
So the two points of intersection are x = 5 and x = -3.
Next, we need to determine which function is on top in the region
between these two intersection points.
For x < -3, the function f(x) = x + 10 is on top.
For -3 < x < 5, the function f(x) = x^2 - x - 5 is on top.
For x > 5, the function f(x) = x + 10 is on top.
To find the area, we integrate the absolute difference between the two functions over the interval [-3, 5].
∫[from -3 to 5] |(x^2 - x - 5) - (x + 10)| dx
Simplifying, we have:
∫[from -3 to 5] |x^2 - 2x - 15| dx
Now, we split the integral into two parts based on the intervals where the absolute value changes its sign.
∫[from -3 to 5] (x^2 - 2x - 15) dx + ∫[from -3 to 5] -(x^2 - 2x - 15) dx
Integrating each part separately, we obtain:
[(1/3)x^3 - x^2 - 15x] from -3 to 5 - [(1/3)x^3 - x^2 - 15x] from -3 to 5
Simplifying further, we get:
[(1/3)(5)^3 - (5)^2 - 15(5)] - [(1/3)(-3)^3 - (-3)^2 - 15(-3)]
Calculating the values, we find:
[125/3 - 25 - 75] - [-27/3 - 9 + 45/3]
The final result is the absolute value of the difference of these two values.
Learn more about intersection here:
https://brainly.com/question/12089275
#SPJ11
Two events are independent. The probability that you are going to see the movie in theater one is 25%. The probability that you will sit in the front row is 10%. What is the probability that you will see the movie in theater one and sit in the front row
Answers
The probability that we will see the movie in theater one and sit in the front row is (D) 2.5%.
What is probability?Probability is a branch of mathematics that deals with numerical descriptions of how likely an event is to occur or how likely a proposition is to be true. The probability of an event is a number between 0 and 1, where 0 indicates the event's impossibility and 1 indicates certainty.A probability formula can be used to calculate the probability of an event by simply dividing the favorable number of outcomes by the total number of possible outcomes.To find the probability that we will see the movie in theater one and sit in the front row:
Given -
The probability that you are going to see the movie in theater one is 25%. The probability that you will sit in the front row is 10%.So,
(1/4)(1/10) = 1/40 = .025 Or, 2.5%Therefore, the probability that we will see the movie in theater one and sit in the front row is (D) 2.5%.
Know more about probability here:
https://brainly.com/question/25870256
#SPJ4
The correct question is given below:
Two events are independent. The probability that you are going to see the movie in theater one is 25%. The probability that you will sit in the front row is 10%. What is the probability that you will see the movie in theater one and sit in the front row.
(A) 40%
(B) 35%
(C) 4%
(D) 2.5%
which coordinate pairs make the equation x-9y=12 true?
1. (12,0)
2. (0,12)
3. (3,-1)
4. (0, -4/3
Answers
Answer:
(12,0) and (3, -1) and (0,-4/3)
Step-by-step explanation:
To find if a point makes an equation true, just substitute its x and y values in in the equation and simplify.
1) Let's test the point (12,0). Substitute 12 for x and 0 for y in the equation:
\(x-9y=12\\(12)-9(0)=12\\12-0=12\\12=12\)
12 does equal 12, so (12,0) makes the equation true.
2) Let's test the point (0, 12). Substitute 0 for x and 12 for y in the equation:
\(x-9y=12\\(0)-9(12) = 12\\0-108 = 12\\-108 = 12\)
However, -108 does not equal 12, so (0,12) does not make the equation true.
3) Let's test the point (3, -1). Substitute 3 for x and -1 for y in the equation:
\(x-9y=12\\(3)-9(-1) = 12\\3 + 9 = 12\\12 = 12\)
12 does equal 12, so (3, -1) makes the equation true.
4) Let's test the point (0, -4/3). Substitute 0 for x and -4/3 for y in the equation:
\((0) -9(-\frac{4}{3} ) = 12\\0 + \frac{36}{3} = 12\\0 + 12 = 12 \\12 = 12\)
12 does equal 12, so (0, -4/3) makes the equation true.
Need help with this please
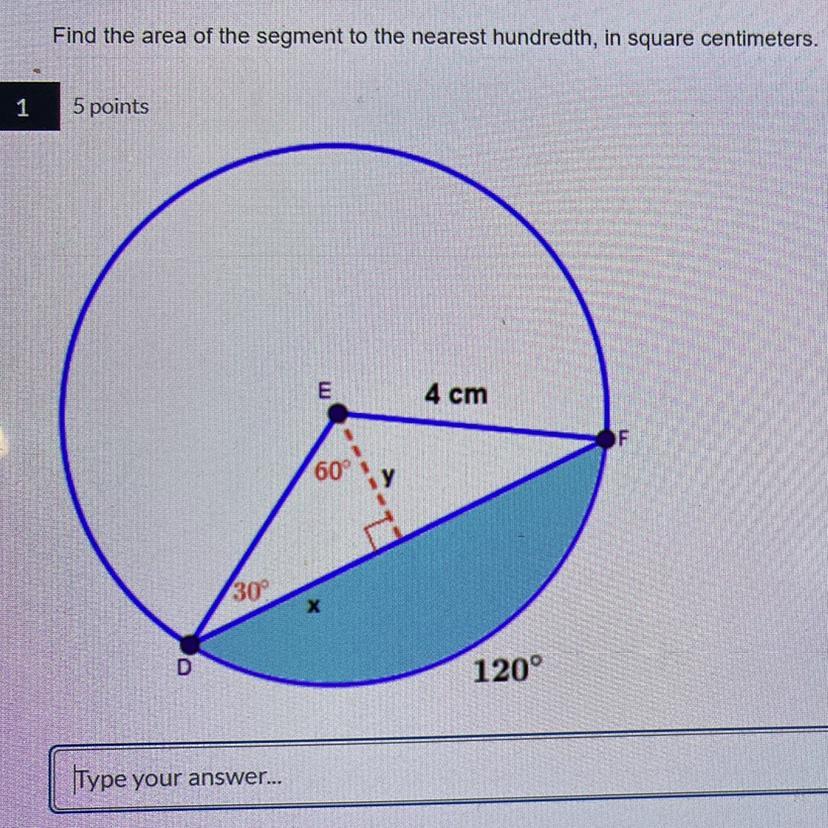
Answers
Answer: 2 cm
Step-by-step explanation:
Because the two right triangles formed by the dashed segment are congruent (which can be proven by ASA), we know that we have a 30 60 90 triangle where the hypotenuse has a length of 4 cm and we need to find the length of the segment opposite the 30-degree angle.
Since the length of the opposite the 30 degree angle is half the length of the hypotenuse in a 30 60 90 triangle, we know that y = 4/2 = 2.
What are geometric solids with circular cross sections? What are they used for? How are they created?
Answers
Geometric solids with circular cross-sections include cylinders, cones, and spheres. Geometric solids with circular cross-sections include cylinders, cones, and spheres. And Cylinders, cones, and spheres can be created by rotating a two-dimensional shape about an axis.
1. Cylinder: A cylinder is a 3-dimensional solid that has two parallel circular bases connected by a curved surface. Cylinders are commonly found in everyday objects like soda cans and water bottles.
2. Cone: A cone is a 3-dimensional solid that has a circular base and a curved surface that tapers to a point. Cones are often used in architecture, like on the top of a church steeple.
3. Sphere: A sphere is a 3-dimensional solid that has a circular shape in all directions. Spheres are found in many natural objects like planets and fruit, as well as in man-made objects like Christmas ornaments.
What are they used for?Geometric solids with circular cross-sections are used in various fields, including architecture, engineering, and science. They are used for creating objects such as cans, pipes, towers, and buildings. These shapes are also used for modeling the natural world, such as the earth, planets, and the stars.
How are they created?Cylinders, cones, and spheres can be created by rotating a two-dimensional shape about an axis. For instance, a circle that is rotated around its center axis forms a cylinder. Similarly, a triangle that is rotated around one of its sides forms a cone, while a circle that is rotated around its center axis forms a sphere.
To know more about geometric solids: https://brainly.com/question/29161618
#SPJ11
You have two sets of data. One has an R^2 value of 0.95. the other has an R^2 value of 0.81. Which one is more linear (that is, the data more nearly fits onto a single line)? a. The one with R^2 = 0.95 is more linear b. The one with R^2 = 0.81 is more linear c. They are equally lineard. It is impossible to determine this from the information given.
Answers
As there is a greater linear relationship between the variables in the data set with an R² value of 0.95, it is more linear. The solution given in option a, "The one with R² = 0.95 is more linear," is correct.
In a linear regression model, the coefficient of determination, or R², quantifies the percentage of the dependent variable's variation that is explained by the independent variable(s).
Strong linear relationships between the variables are indicated by an R² value that is close to 1, whereas weak linear relationships are indicated by a value that is close to 0.
Therefore, Because there is a stronger linear relationship between the variables in the data set with an R² value of 0.95 than in the data set with an R² value of 0.81, it is more linear.
The more closely the data points are grouped around a single line, the stronger the linear relationship, and the closer the R² number is to 1.
Therefore, We can deduce that the proper response is an option a, "The one with R²= 0.95 is more linear." Write your response in two lines.
To learn more about linear regression, visit the link below:
https://brainly.com/question/29665935
#SPJ4
HELP FAST Easy FAST

Answers
Should be (-6, 0) because if you extend the line it would most likely cross into (-6), I doubt it would extend long enough to reach (-8).
Seven less than the product of a number n and 1/6 is no more than 94
Answers
Answer:
n ≤ 606Step-by-step explanation:
Seven less than the product of a number n and 1/6 is no more than 94, translating:
n*1/6 - 7 ≤ 94Solving for n:
n/6 ≤ 94 + 7n/6 ≤ 101n ≤ 101*6n ≤ 606Finding the side length of a cube from its Volume in liters A technical machinist is asked to build a cubical steel tank that will hold 275 L of water. Calculate in meters the smallest possible inside length of the tank. Round your answer to the nearest 0.001 m. X 5 ?
Answers
The smallest possible inside length of the cubical steel tank that can hold 275 liters of water is approximately 0.640 meters.
The side length of the cube is found by converting the volume of water from liters to cubic meters, as the unit of measurement for the side length is meters.
Given that the volume of water is 275 liters, we convert it to cubic meters by dividing it by 1000 (1 cubic meter = 1000 liters):
275 liters / 1000 = 0.275 cubic meters
Since a cube has equal side lengths, we find the side length by taking the cube root of the volume. In this case, we find the cube root of 0.275 cubic meters:
∛(0.275) ≈ 0.640
Rounded to the nearest 0.001 meters, the smallest possible inside length of the tank is approximately 0.640 meters.
To know more about smallest possible inside length, refer to the link :
https://brainly.com/question/17304098#
#SPJ11
Use polar coordinates to find the volume of the given solid.
Below the paraboloid z = 18 − 2x² − 2y² and above the xy-plane
Answers
V = π [(3(\(\sqrt{18/2}\))³/1) - (2(\(\sqrt{18/2}\))⁵/15)] - π [0]
Simplifying this expression will give us the final volume of the solid.
, we need to evaluate the triple integral:
V = ∫₀²π ∫₀ᵣ ∫(18 - 2r²) r dz dr dθ
Integrating with respect to z first, we have:
V = ∫₀²π ∫₀ᵣ (18 - 2r²) r dr dθ
Integrating the volume with respect to r, we get:
V = ∫₀²π [(9r² - 2/3r⁴)]ᵣ₀ dθ
Simplifying the expression inside the brackets and evaluating the integral, we have:
V = ∫₀²π (9r² - 2/3r⁴) dθ
V = π [(9/3)r³ - (2/15)r⁵]ᵣ₀
V = π [(3r³/1) - (2r⁵/15)]ᵣ₀
Learn more about volume here:
https://brainly.com/question/28058531
#SPJ11
A bag contains two pencils , one ruler and five pens . What is the probability of randomly selecting a pen , a ruler and a pencil without replacement
Answers

The probability of randomly selecting a pen, a ruler, and a pencil without replacement from the given bag is 5/168.
We have,
Pencils= 2
Ruler = 1
Pens = 5
Total items in the bag: 2 pencils + 1 ruler + 5 pens = 8 items
Now, the Probability of selecting a pen first
P(pen) = 5/8
and, Probability of selecting a ruler second
P(ruler) = 1/7
and Probability of selecting a pencil last
P(pencil) = 2/6 = 1/3
So, the overall probability is
P(pen, ruler, pencil) = P(pen) x P(ruler) x P(pencil)
= (5/8) x (1/7) x (1/3)
= 5/168
Therefore, the probability of randomly selecting a pen, a ruler, and a pencil without replacement from the given bag is 5/168.
Learn more about Probability here:
https://brainly.com/question/31828911
#SPJ2
Translate the phrase into an algebraic expression.
The difference of c and 3
Answers
Answer: c-3
Step-by-step explanation:
it is wanting you to take c minus 3
At 7:00am two groups of hikers begin 21 miles apart and head toward each other on the trail. The first group, hiking at an average of 1.5 miles per hour, carries tents, sleeping bags, and cooking equipment. The second group, hiking at an average speed of 2 miles per hour, carries food and water. How long it will be until the two groups of hikers meet. (hint solution sentence)
Answers
Answer: 6 hours
Step-by-step explanation:
The question asks how long until they meet.
First, you add 1.5 miles per hour and 2 miles per hour to get 3.5 miles per hour.
Then you divide 21/by 3.5 which gets you how many hours it takes for them to meet.
Which means 21/3.5 is 6 hours.
Bob and James are finishing the roof of a house. Working alone, Bob can shingle the roof in 10 hours. James can shingle the same roof in 16 hours. How long will it take them working together to shingle the roof? Round your answer to the nearest hundredth if necessary.
Answers
1/10 + 1/16 = 1/t
8/80 + 5/80 = 1/t
13/80 = 1/t
Cross multiply
13(t) = 1(80)
13t = 80
t = 6.15
It would take them 6.15 hours to complete the roof together.
=========================================================
Work Shown:
x = amount of time it takes for Bob to do the job alone
x = 10 hours
y = amount of time it takes for James to do the job alone
y = 16 hours
z = amount of time it takes for them to work together
z = (x*y)/(x+y)
z = (10*16)/(10+16)
z = 160/26
z = 6.1538 approximately
z = 6.15
They will take about 6.15 hours if they work together, and if neither person slows the other down.
-------------------
Another approach (optional section):
Let's say there are 80 shingles needed to cover the roof.
If Bob needs 10 hours when working alone, then his rate is 80/10 = 8 shingles per hour.
If James needs 16 hours when working alone, then his rate is 80/16 = 5 shingles per hour.
Their combined rate is 8+5 = 13 shingles per hour.
h = number of hours they work together
13h = number of shingles they can do after h number of hours
13h = 80
h = 80/13
h = 6.15 approximately
We get the same answer as before.
what is 7+(6*5^2+3)
Answers
Factor x²−16 completely, SHOW STEPS PLEASE
Answers
Answer: (x +4)(x - 4)
Step-by-step explanation: Since x² - 16 represents the difference of two squares, it can be factored as the product of two binomials, one that has a plus in it and one that has a minus in it.
The first position in each binomial is filled by
the factors of x² that are the same, x times x.
The second position in each binomial is filled
by the factors of 16 that are the same, 4 times 4.
The answer therefore is (x + 4)(x - 4).
